基于单纯形法改进的混沌控制算法

夏雨 汤峰 余颖烨

摘   要：混沌控制（chaos control，CC）算法在求解结构可靠度问题中具有优越的稳健性，但由于其对步长的严格限制，导致计算速度较慢。单纯形法是一种不将梯度方向作为寻优方向的算法，该算法初始计算速度较快，能够迅速逼近至极限状态面附近，此后计算速度明显下降，且计算结果误差较大。为此，提出一种基于单纯形法改进的混沌控制算法。首先，通过增广乘子法将可靠度计算中的非线性等式约束问题转化为非约束问题;然后，通过单纯形法进行初始迭代计算;最后，使用CC算法进行收敛计算。算例结果表明：本文算法能够有效解决高非线性功能函数可靠度求解问题，且兼具两种算法的优点，与混沌控制算法相比，提高了计算效率。

关键词：结構可靠度;混沌控制算法;单纯形法;可靠度计算;计算效率

中图分类号：TU311.4                DOI：10.16375/j.cnki.cn45-1395/t.2022.03.008

0    引言

建筑结构的安全性与稳定性对人类社会影响巨大，如何对其进行合理评价至关重要。Freudenthal[1]在《结构安全度》一文中提出了结构可靠度的相关概念;为了得到结构可靠度指标，Cornell等[2-4]提出了一次可靠度理论，并对其不断完善。然而当结构功能函数的非线性程度较大时，经典一次可靠度计算方法往往会出现迭代振荡、结果不准确的情况。为了解决上述问题，众多学者展开了更进一步的研究。Liu[5]首先考虑引入merit函数作为评价函数，但是该函数并不能保证算法的迭代方向为下降方向;Zhang等[6]考虑引入Armijo准则进行迭代步长的调控;杨迪雄[7]基于混沌控制理论中的稳定转换法，通过引入步长调控因子提出了混沌控制（chaos control，CC）算法，但由于该方法对步长的严格限制，致使算法计算速度相对较慢;Meng等[8]针对CC算法中存在的问题，结合“之”字型迭代路径，提出了修正混沌控制（modified chaos control，MCC）方法。目前学术界对于Armijo准则的研究也有了不少的成果[9]，而李彬等[10-11]则将Armijo准则引入到混沌控制算法中，使得计算速度进一步加快，并且进行了逆可靠度求解方法的尝试。与此类似，亢战等[12]提出的修正迭代算法中也提及了步长调控因子的控制作用，在文中将其定义为修正系数，并给出了修正系数的具体计算方法。

除此之外，贡金鑫[13]还对迭代点在极限状态面上的负梯度方向进行了深入研究讨论，提出了有限步长法，并推理出HL-RF算法只是有限步长法的一个特例，该方法的初始步长会影响算法的收敛性。吴狄等[14]提出了自动变步长的搜索方法，但是收敛速度较慢。王林军等[15]使用外罚函数法进行可靠度计算，但是由于该方法将其中一个变量用剩余变量进行表示，算法鲁棒性不好，不够稳定，应用受限。高翔等[16]则将模拟退火法与增广乘子法应用到可靠度计算中，虽然避免了一次二阶矩方法中梯度的求解问题，但是却增加了迭代步骤。许家赫等[17]将自适应性PSO算法与fmincon函数结合用于寻优计算，拓展了可靠度指标的计算方法。就目前而言，FOSM方法在结构可靠度分析方面的理论研究已经比较成熟，但是在实际的工程可靠度分析中却鲜有使用，主要原因是：如果结构的功能函数非线性程度过高，那么将会导致求解过程复杂化，致使整个计算过程效率低下，误差也比较大，所以如何实现快速、准确求解是当前有待解决的一个     问题。

针对上述问题，本文提出一种基于单纯形法改进的CC算法。首先，通过增广乘子法将可靠度计算中的非线性等式约束问题转化为非约束问题;然后，通过单纯形法进行初始迭代计算;最后，使用CC算法进行收敛计算，通过数值算例验证了本文方法的计算准确性与效率。

1    可靠度理论

Cornell[2]提出将结构构件的均值与标准差的比值作为该构件的可靠度指标，并以此建立了一次二阶矩方法，但是该方法在实际应用中存在一定的缺陷。Hasofer和Lind重新定义了结构可靠度指标的概念，确保了可靠度指标在同一构件不同极限状态函数下的唯一性，对可靠度理论进行了完善与修正。在数学上，可靠度指标[β]可以定义为如下非线性约束优化问题：

[minβ=d（X*）=i=1nx*i2] ， （1）

[s. t.   G（X）=g（x1， x2， …， xn）=0] . （2）

式中：[x]是标准正态空间下的随机变量，[G（X）]为结构的功能函数，[β] 是结构可靠度指标。结构可靠度的几何意义是标准正态空间下，结构功能函数上一点到原点的最短距离。对于不服从正态分布的随机变量，可以使用JC法将其当量正态化。该方法的前提条件是验算点[x*i] 处[X'i]和[Xi] 的累积分布函数和概率密度函数分别对应相等，由此可以得到正态化之后的变量均值与标准差：

[ux′i=x*i-Φ-1[FXi（x*i）]σx′i] ，           （3）

[σx′i=ϕ{Φ-1[FXi（x*i）]}fXi（x*i）] .               （4）

式中：[Φ（⋅）] 为标准正态的分布函数，而[ϕ（⋅）] 为标准正态分布的概率密度函数，[ux′i] 是随机变量当量正态化后的均值，[σx′i] 是随机变量当量正态化后的标准差。在得到当量正态化后的变量均值与标准差之后便可以进行可靠度计算。

2    CC算法与单纯形法计算原理

2.1   CC算法

在可靠度计算方法中，经典HL-RF算法由于其概念清晰、计算简便等优点，被广泛用于结构可靠度求解，其核心思想是将结构功能函数在第k个迭代点进行一阶泰勒展开，并使功能函数在第k+1个迭代点的函数值满足[g（uk+1）=0] ，可得：

[g（uk）+∇g（uk）T（uk+1-uk）=0] .  （5）

令第k+1次迭代点到标准正态空间下原点的距离为[βk+1] ，并取[uk] 点处梯度负方向的单位向量作为迭代选取方向，得：

[uk+1=-βk+1∇g（uk）∇g（uk）] . （6）

结合式（5），可得：

[βk+1=g（uk）-∇g（uk）Tuk∇g（uk）] . （7）

式（6）与式（7）合称为HL-RF算法，其在解决低非线性功能函数可靠度求解问题时计算效率很高，能够在迭代过程中逐渐靠近收敛点。但是在解决高非线性功能函数时，往往会出现迭代振荡，甚至不收敛的情况。

为了提高HL-RF算法的收敛性，杨迪雄[7]采用混沌控制学理论对其进行改进，提出了CC算法。该算法引入混沌控制因子对迭代过程中的振荡情况进行了控制，表达式变为：

[uk+1=uk+λC[F（uk）-uk]] ， （8）

[F（uk）=[∇g（uk）]Tuk-g（uk）∇g（uk）2∇g（uk）] . （9）

式中：[C]代表n×n维对合矩阵，一般情况下取单位矩阵，[λ]是一个常数，代表混沌控制因子。通過上式可以发现，CC算法相较于经典HL-RF算法而言，补充了迭代步长控制计算步骤。先通过HL-RF算法求解出[F（uk）]点，然后以本次迭代点[uk]为基点，将[uk]到[F（uk）]点的方向作为迭代方向，并在该迭代方向上选取一定的步长。如果[λ=0] ，则[uk+1=uk]，无法进行迭代计算;如果[λ=1]，则可得[uk+1=F（uk）]，此时的迭代公式就变成了经典HL-RF算法，所以[λ]的取值为0 ～ 1。为了保证收敛性，[λ]的取值一般设置为较小的常数，导致CC算法的步长较小，收敛速度较慢。如果能使CC算法初始计算点尽可能靠近MPP点，就可以减少计算量，加快算法整体收敛速度。

2.2   单纯形法

单纯形法是一种不将函数梯度信息作为下降方向的算法。该算法在计算初始阶段，收敛速度较快，具有一定的计算优势，但是在贴近极限状态面之后，计算速度反而开始下降，且单纯形法是一种

用于计算无约束问题的算法，根据式（1）、式（2）可知，结构可靠度的计算属于有约束问题。通过增广乘子法可以将有约束的可靠度计算问题转变为无约束优化模型[Mρ]。

[Mρ（X， r， ρ）=i=1n（Xi-μiσi）2+]

[r2j=1n[gj（Xi）]2+j=1nρjgj（Xi] [）].       （10）

式中：[ρ=[ρ1， ρ2， …， ρm]] 为拉格朗日乘子，[r]为罚函数的惩罚因子，[r2j=1n[gj（Xi）]2] 为乘子项，[j=1nρjgj（Xi）] 为惩罚项。

通过增广乘子算法对功能函数与可靠度指标计算公式进行结合，使得单纯形法可以用于可靠度问题的求解。该算法的基本思想是：根据未知变量的个数，选择n+1个不同的点构成正单纯形，分别计算正单纯形的n+1个顶点函数值，对比优劣，找到函数值最大的点及函数下降方向，据此来搜索新的点代替最大值点，依次更迭。在迭代点未接近极限状态面时，[Mρ]优化模型中的惩罚项发挥主要作用，迫使算法向极限状态面逼近;而当迭代点逼近至极限状态面附近，惩罚项与乘子项趋近于0，此时可靠度指标的计算公式便可以发挥主要作用，使点通过迭代逐步逼近到最有可能失效点附近，并求得可靠度指标，该算法的迭代示意图如图1所示。

图1中，由x3、[x1]与x2  3个点共同组成一个单纯形，3个点分别为单纯形的3个顶点。x3为极差点，xc为反射基点，xD为反射点，xR为延伸点，xp为收缩点。

根据单纯形法的基本思想，该理论只适合无约束函数的计算，而增广乘子法可以将约束优化问题转化为无约束优化问题，这样单纯形法就可以进行可靠度求解。计算步骤如下所示：

Step  1   将[Mρ]作为目标函数，选取均值点[x11=（x111， x112， …， x11n）T]作为初始点，并将其视为初始单纯形的一个顶点，采用式（11）计算正单纯形剩余顶点的坐标[19]：

[x12=x11+（d1， d2， d2， …， d2）T，x13=x11+（d2， d1，d2，…， d2）T，x14=x11+（d2， d2， d1，…， d2）T，                         ⋮ x1n+1=x11+（d2， d2， d2， …， d1）T.]       （11）

其中，[d1=sn2（n+1+n-1）]，[d2=sn2]

[（n+1-1）]，[s]为初始正单纯形的边长。

Step  2   计算[n+1]个正单纯形顶点的函数值，并找出其中的最好点[（][x1][）]与最差点[（][x3][）]，然后计算除最差点外剩余点的中心点xc，以此作为基点。

Step  3   以xc点为反射基点，[x3]通过该点进行反射，得到[xD=xc+α（xc-x3）]，其中常数取[α=1][18]，并计算函数值。

Step  4   判断[Mρ（xD）]的大小。如果[Mρ（xD）≤Mρ（x1）]，则转至Step  5;如果[Mρ（x1）<Mρ（xD）<Mρ（x3）]，则由[xD]代替[x3];如果[Mρ（xD）≥Mρ（x3）]，则转至Step  6。

Step  5   进行延伸计算，从而得到[xR=xc+γ（xD-xc）]，常取[γ=2][18]，并计算函数值[Mρ（xR）]。如果[Mρ（xR）<Mρ（xD）]，则由[xR]代替[x3];否则由[xD]代替[x3]。

Step  6   [xp=xc+σ（x3-xc）]，常取[σ=0.5][18];如果[Mρ（xp）<Mρ（x3）]，则由[xp]代替[x3]，否则转至Step  7。

Step  7   如果经过收缩之后的点仍无法满足计算要求，则说明该单纯形构型需要重新构建，除了最优点外的所有点都沿着本点到最优点的方向移动一半距离，即[xi=x1+δ（xi-x1）]，常取[δ=0.5][18]，转至Step  8。

Step  8   判断算法的收敛情况。如果[1n+1i=1n+1[（Mρ（xi）-Mρ（xc）） ]2 ≤ε]，迭代停止，输出计算结果;否则[k=k+1]，转至Step  2。

单纯形法能够在计算初期迅速将迭代点拉近至极限状态面附近，但是该算法的缺点是：在迭代点靠近极限状态面之后会出现计算速度下降、计算结果不准确、误差较大的情况。

3    基于单纯形法改进CC算法

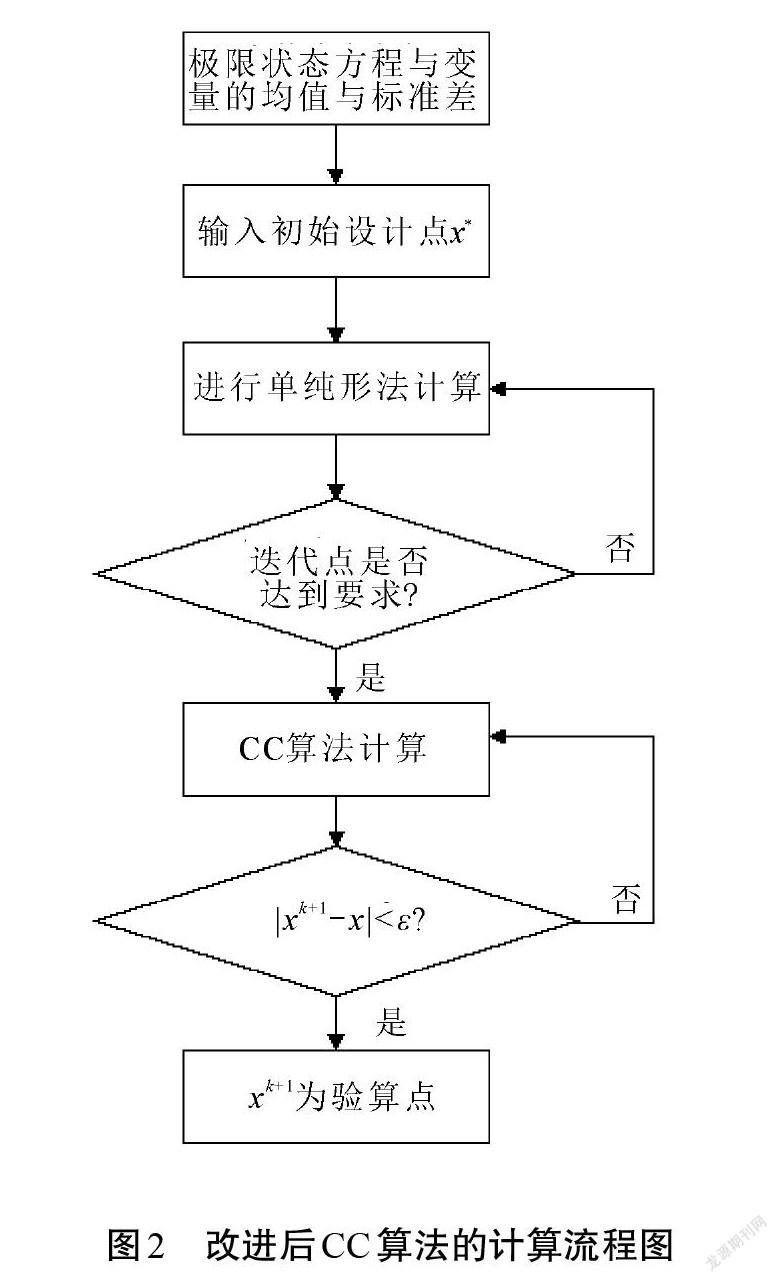
基于单纯形法的优点与CC算法存在的不足之处，本文提出基于单纯形法改进的CC算法。对于初始迭代点，先使用单纯形法进行迭代计算，将点拉近至极限状态面之后，再采用CC算法进行收敛计算。具体计算流程如图2所示。

在改进CC算法的计算过程中，最为核心的是如何判断迭代点已经达到进行CC算法的计算条件。对此，有2种判断方案可供选择：第一种是考虑经过单纯形法迭代计算之后的点是否已经接近极限状态面;第二种是考虑单纯形的尺寸，即当单纯形的尺寸到达一个阈值之后，则转入CC算法计算。由于单纯形法本身并不适用于有约束问题的求解，经过增广乘子法改进后的单纯形法虽然也可以进行可靠度求解计算，并在计算初期迅速将点拉近至极限状态面，但是该方法会出现各个顶点在接近极限状态面之前，单纯形尺寸已经缩小到算法终止准则，进而导致后续计算无法进行。所以本文选择第二种方法，将单纯形尺寸的阈值作为判断依据。

4    算例分析

本文算例中混沌控制因子[λ=0.1]，且本文方法

选取均值点作为初始正单纯形的一个顶点，通过计算得到的其他正单纯形顶点属于算法中辅助计算的点，并且在后续进行CC算法的计算时并不参与最终的求解计算。所以本文方法迭代图中只显示初始均值点在整个算法过程中转换到标准正态空间U下的迭代路径。

算例1

假设功能函数形式为：

[Z=x31+x32-4] .                 （12）

本算例中各随机变量相互独立且服从正态分布，[x1～N（3.0， 1.0）]和[x2～N（2.9， 1.0）]。求解该算例的可靠度指标。

先将各变量转换到标准正态空间下，然后再进行计算，选择初始正单纯形边长[s=1]。图3为CC算法的迭代路径图。由图3可以看到，该功能函数在验算点处的非线性程度较大，CC算法沿着几乎呈现线性的迭代路径以极小的步长向验算点处进行迭代，最终收敛。图4为本文方法的迭代路径图。从图4可以看出，该方法很好地融合了单纯形法与CC算法的优势，计算前期能够迅速逼近至极限状态面附近，而后逐步向验算点处收敛。从表1的计算结果来看，本文方法与CC算法并无差别，但迭代次数明显减少，计算速度得以提升。

算例2

假设功能函数为：

[Z=x41+2x42-20]  .             （13）

其中，各随机变量相互独立，为[x1～N（10.0， 5.0）]和[x2～N（10.0， 5.0）]，求解可靠度指标。

同样先将功能函数中的变量进行标准正态转换，而后计算，初始正单纯形边长[s=1]。图5与图6分别为CC算法与本文方法的迭代图，功能函数在验算点处非线性程度比较大。CC算法沿着一条呈现出顺滑曲线的迭代路径进行迭代，速度相对较慢。本文方法中首次迭代就将点拉近到极限状态面附近，为后续的可靠度求解计算节省了大量的计算步骤。由表2的计算结果来看，本文方法与CC算法基本一致，且迭代次数更少，效率更高。

算例3

假设极限状态方程为：

[Z=u3-（u1-1）2-1.5（u2-2）2] .     （14）

该方程含有3个随机变量[u1]、[u2]、[u3]，均服从独立标准正态分布且互不相关，计算可靠度指标。

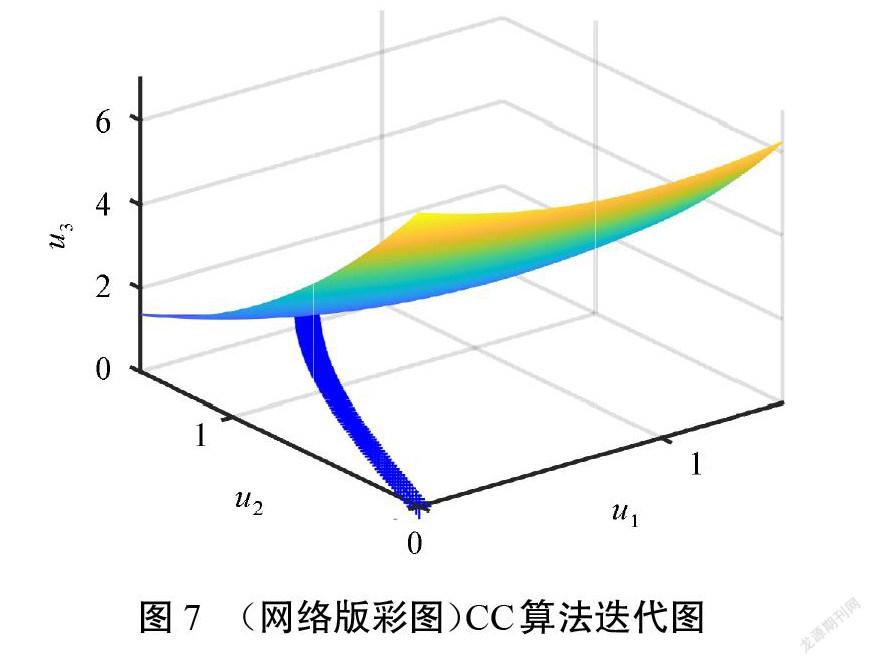
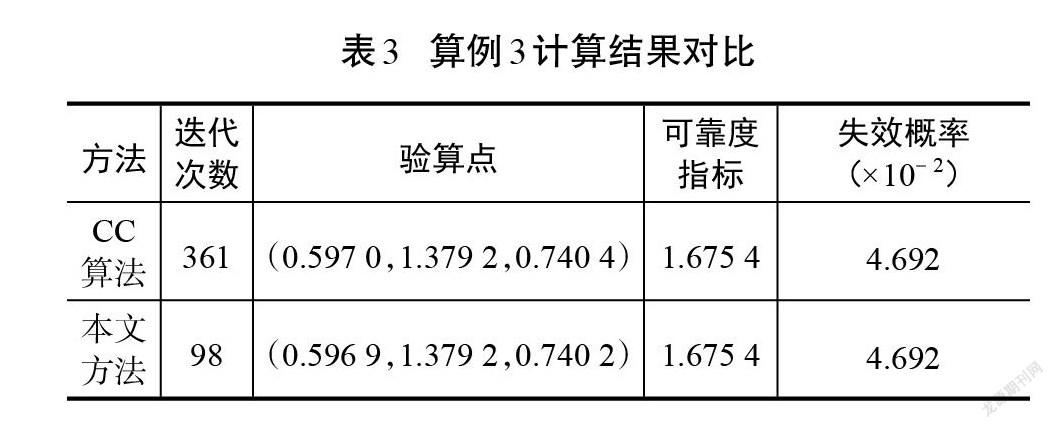
该算例中的随机变量均服从标准正态分布，不需要进行标准正态转换。由于该功能函數为三维高非线性，所以缩小初始正单纯形边长为[s=0.1]。迭代路径图如图7和图8所示。CC算法迭代过程仍然是一条顺滑的曲线，但是本文方法在迭代计算初期就迅速将点拉近到极限状态面附近，有效缩短了后续计算时间，计算结果如表3所示。从表3来看，本文方法与CC算法的计算结果并无太大差别，但迭代次数更少，计算速度更快，说明本文方法具有一定的优势。

5    结论

当功能函数在验算点处非线性程度较高时，CC算法迭代路径往往会呈现一条明晰的曲线，而本文方法则可以依靠单纯形的最初几步迭代计算就能迅速将点拉近到极限状态面附近，最后通过CC算法进行计算，有效节省了计算时间。通过算例计算表明，本文方法不仅计算结果与CC算法基本一致，而且还减少了迭代次数，迭代次数仅为 CC算法的1/4～1/2，证明了本文方法兼具准确性与计算速度。

参考文献

[1]    FREUDENTHAL  A  M. The safety of structures[J].Tranactions of the American Society of Civil Engineers， 1947， 112（1）：125-159.

[2]     CORNELL  C  A. A probability-based structural code[J].Journal of American Concrete Institute，1969， 66（12）：974-985.

[3]     HASOFER  A  M，LIND  N  C. Exact and invariant second moment code format[J].Journal of Engineering Mechanics，1974，100（1）：111-121.

[4]     RACKWITZ   R，FLESSLER  B. Structural reliability under combined random load sequences[J]. Computers and Structures， 1978， 9（5）：489-494.

[5]     LIU   P   L. Optimization algorithms for structural reliability[J]. Structural Safety， 1991， 9（3）：161-177.

[6]     ZHANG  Y， KIUREGHIAN A D. Two improved algorithms for reliability analysis[M]//Reliability and Optimization of Structural Systems. Boston：Springer，1995：297-304.

[7]     杨迪雄. 结构可靠度分析FORM迭代算法的混沌控制[J]. 力学学报， 2007，39（5）：647-654.

[8]     MENG  Z， LI  G， YANG  D  X，et al. A new directional stability transformation method of chaos control for first order reliability analysis[J]. Structural and Multidisciplinary Optimization， 2017， 55（2）：601-612.

[9]     韦春妙， 庞建华， 黄李韦， 等. 新Armijo线搜索下的PRP共轭梯度法及其收敛性分析[J]. 广西科技大学学报， 2019，30（2）：107-114.

[10]   李彬， 李刚. 基于Armijo准则的自适应稳定转换法[J]. 计算力学学报， 2018， 35（4）：399-407.

[11]   李彬， 郝鹏， 孟增， 等. 基于改进自适应混沌控制的逆可靠度分析方法[J]. 应用数学和力学， 2017， 38（9）：979-987.

[12]   亢战， 罗阳军. 计算结构可靠度指标的修正迭代算法[J]. 工程力学， 2008， 25（11）：20-26.

[13]   贡金鑫. 结构可靠指标求解的一种新的迭代方法[J].计算结构力学及其应用， 1995（3）：369-373.

[14]   吴狄， 关鼎. 一种结构可靠性指标的搜索方法[J]. 计算力学学报， 2005，22（6）：788-791.

[15]   王林军， 王锬， 杜义贤， 等. 一种基于外罚函数法的结构可靠性分析方法[J]. 三峡大学学报（自然科学版）， 2019， 41（1）：92-96.

[16]   高翔， 王林军， 杜义贤. 采用增广乘子法和模拟退火法的结构可靠性分析[J]. 西安交通大学学报， 2019， 53（7）：144-152.

[17]   許家赫， 陈岳坪. 改进粒子群算法与fmincon函数混合寻优的平面度、垂直度误差评定[J]. 广西科技大学学报， 2019， 30（4）：105-109.

[18]   刘惟信. 机械最优化设计[M]. 2版. 北京：清华大学出版社， 1994.

[19]   康哲民. 基于响应面法的结构可靠性分析及应用[D]. 柳州：广西科技大学， 2019.

Improved chaos control algorithm based on simplex method

XIA Yu， TANG Feng， YU Yingye

（ School of Civil Engineering and Architecture， Guangxi University of Science and Technology，

Liuzhou  545006，  China）

Abstract： Chaos control（CC） algorithm has superior robustness in solving structural reliability problems， but the strict restriction for step size makes calculation speed low. Simplex method is an algorithm that does not take the gradient direction as the optimization direction. The initial calculation speed of the simplex method is fast. And it can approach to the limit state surface quickly at the beginning of calculation， after that， the calculation speed decreases obviously and the error of calculation results is large. In this paper， an improved chaos control algorithm based on simplex method is proposed. Firstly， the nonlinear equation constraint problem in reliability calculation is transformed into unconstrained problem by the augmented multiplier method.  Then， the simplex method is used for initial iterative calculation.  Finally， CC algorithm is used for convergence calculation.  The numerical results show that the proposed algorithm can solve the reliability problem of high nonlinear function effectively and has the advantages of both algorithms. Compared with the chaos control algorithm， the proposed algorithm improves the calculation efficiency.

Key words： structure reliability; chaos control algorithm; simplex method; reliability calculation; calculation efficiency

（ 責任编辑：罗小芬）