考虑动态度和时间窗的两级车辆路径问题
2022-07-07林明锦王建新
林明锦,王建新,王 超
(1.重庆大学 机械与运载工程学院,重庆 400044;2.太原理工大学 经济管理学院,山西 太原 030002;3.北京工业大学 经济与管理学院,北京 100124)
0 引言
随着经济的全球化、移动互联网技术的日趋成熟以及物流基础设施的完善,以集群式供应链为支撑的集成制造模式得以快速发展。在企业层面,由于受不同制造中心(以下简称客户)主生产计划的制约、市场需求波动导致产量变更等不确定因素的影响,各级供应商不仅需要按照主生产计划将客户所需的零部件按时配送给客户,还要尽可能地动态调整配送计划以满足客户的动态不确定需求,以提升市场响应能力,这使得各大供应商求解面向客户动态需求的带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW)变得愈加复杂[1]。传统制造业的供应商更多关注如何在满足时间要求并遍历有限客户的约束下寻找起止于配送中心的最短车辆路径,现代供应商为快速响应客户动态需求,开始倾向于在能够辐射客户的区域建立快速响应客户的中转站。在政策方面,随着北京、上海、广州、重庆等地中重型货车24/12小时限行相关政策试点的实施,跨省市长途运输的大型货车直接为客户提供送货服务受到了严格限制,迫使供应商选择以中转站为分界点,采用不同额定运力的车辆满足干线与支线零部件供应的需求,进一步催生了对考虑动态度和时间窗的两级车辆路径问题(Two-Echelon Vehicle Routing Problem with Time Window considering Dynamic Degree, 2E-VRPTWDD)的研究。
2E-VRPTWDD是两级车辆路径问题(Two-Echelon Vehicle Routing Problem, 2E-VRP)的进一步扩展,其中一级路径为车辆从配送中心出发遍历所有中转站时形成的路径,二级路径为车辆由中转站出发遍历所有客户时形成的路径。在服务集成制造系统的物流运输中,2E-VRPTWDD指在制造单元时间和动态需求约束下,将零部件从配送中心到客户的配送过程划分为两级,一级配送网络的节点要素包括配送中心和中转站,二级配送网络的节点要素包括中转站和客户。供应商则通过两级协调运作,为客户提供响应市场波动需求的零部件供应服务。
针对2E-VRP,葛显龙等[2]以两级配送中车辆的总配送距离为目标函数,构建了基于场景动态度的两级配送网络优化模型,并采用禁忌搜索算法求解约束优化模型,然而该模型并未考虑客户对个性化时间窗的现实需求;YAN等[3]研究了冷链物流配送中两级配送的中心选址问题,但在选址过程中未考客户的动态度;LIU等[4]研究了具有客户需求更新的两级物流供应商批量订购策略,所提需求更新策略对动态车辆路径问题的研究具有借鉴意义;MU等[5]构建了带有时间约束的阶段性车辆路径优化模型。路径优化约束模型的求解方法分为以分支界定法[6]、动态规划法[7]为主的精确式求解方法,以及以模拟退火算法[8]、遗传算法[9]等为代表的启发式算法。为了在短时间内获得路径优化问题的近似最优解,较多文献采用启发式算法求解车辆路径问题约束优化模型。例如,WEI等[8]采用模拟退火算法,具体求解过程为随机生成初始解,判断是否满足约束条件,随后随机生成满足约束条件的新解,并对比新解与旧解,根据模拟退火准则判断是否接受新解,直到达到设计好的终止条件,输出算法的最好解;LI等[9]采用遗传算法,与模拟退火算法的不同在于新解的生成规则以及解的接受规则,遗传算法的新解主要通过交叉和变异产生,是否接受解则由适应度函数决定。其他求解车辆路径优化约束模型的方法还包括离散布谷鸟算法[10]、蚁群算法[11]、粒子群优化算法[12]、迭代变邻域下降算法[13]等。针对多目标优化的建模问题,KAROONSOONTAWONG等[14]构建了用于求解VRPTW的层次多目标模型(hierarchical multi-objective formulation),ZHANG等[15]构建了两级优化模型,VINCENT等[16]构建了字典序优化模型。这3种多目标优化模型均在数学模型中设置了多个目标函数,不同在于求解规则,层次多目标模型是通过算法求解多目标问题,即先对主目标进行优化,再在主目标非劣化的情况下对次目标进行优化[14];两级优化模型是将最小化的目标函数作为约束嵌入约束条件[15];字典序优化模型则是通过在满足第1个目标的可行解范围内寻找满足第2个目标的最佳可行解,在满足第2个目标的可行解范围内寻找满足第3个目标的最佳可行解,依次类推,最终找到满足多目标的可行解[16]。
综上可知,现有文献针对2E-VRP,已从不同角度展开了深入研究并取得一定成果,然而鲜有文献从考虑客户动态需求与时间要求的角度对2E-VRP进行研究。另外,客户的动态度越大,对路径优化的挑战性越高,然而少有文献以动态度为指标对2E-VRP进行差异优化,以尽可能满足客户需求动态化与时间个性化的要求。因此,本文在借鉴现有2E-VRP研究成果基础上,设计了基于动态需求获取准则及满足客户动态需求的差异策略,并将其融入所构建的2E-VRPTWDD优化模型,旨在为提升供应商对客户动态需求的快速响应力提供理论支撑。为提升求解2E-VRPTWDD的效率,对串行模拟退火算法的初始方案生成规则和邻域搜索策略进行了改进,并借鉴现有并行算法思想设计了改进的并行模拟退火算法,最后以H公司为案例对所设计的方法进行了验证。
1 问题描述及数学模型
1.1 问题描述
所求解的2E-VRPTWDD(如图1)中,在任意静态时间段内均包括2E-VRP网络优化。一级路径中主要优化由配送中心和中转站组成的带时间约束的有向连通子网络,二级路径中主要优化由中转站和客户组成的带时间窗约束的有向连通子网络。其中,动态度指在车辆执行配送任务过程中动态客户与所有客户的比例。由于车辆在执行任务过程中可能出现动态客户,而动态度会随时间的增加而增加,车辆须做出是否响应动态客户的决策,在较小动态度时响应动态客户虽然能够快速满足客户需求,但是配送成本亦随之增加;在较大动态度时响应动态客户,虽然能够降低配送成本,但是不能快速满足客户需求。
2E-VRPTWDD可被描述为两个相关的有向连通网络图中边的选择问题。基本假设为:由于中重型车辆在城市中行驶受限,在不同级配送网络中采用不同类型车辆,在同一级配送网络中采用相同类型车辆;如果可供调度的车辆到达中转站/客户的时间早于中转站/客户的最早时间窗,则需在中转站/客户处等待,但车辆的到达时间不能晚于中转站/客户要求的最晚时间窗;一级配送网络的送达时间窗应满足二级配送网络中客户的时间窗要求;二级配送网络中存在动态客户与静态客户。其中,静态客户指在[Ti,Ti+1]周期内需求量保持不变的客户,动态客户包括在配送过程中新增的客户和原有客户新增需求衍生的新客户。因此,求解问题为在考虑动态度的情形下,使不同级车辆行驶和使用成本最小化。约束条件为:每个中转站/客户均能在一个配送周期内被唯一车辆服务一次,每辆车只服务起讫于配送中心/中转站的一条路径,且满足车辆装载能力、中转站/客户时间窗约束。
本文用到的数学符号及含义如下:
G1,G2为一、二级有向连通网络图,G1=(V1,E1),G2=(V2,E2);
V1,V2为一、二级网络图的节点,V1=V1_d∪V1_c,V2=V2_d∪V2_c;
V1_d,V2_d为一级网络中的配送中心和二级网络中的中转站;
V1_c,V2_c为一、二级网络中服务的节点,其中一级网络中服务的节点类型为中转站,二级网络中服务的节点类型为客户;
N1,N2为一、二级网络中所服务节点的数量;
E1,E2为一、二级网络图的边,E1={(i,j)|i,j∈V1,i≠j},E2={(i,j)|i,j∈V2,i≠j};
c1,c2为一、二级车辆的单位行驶距离成本;
K1,K2为一、二级车辆的集合,K1={1,2,3,…,K1},K2={1,2,3,…,K2};
k为车辆编码,k∈K1∪K2;
Q1_k(k∈K1),Q2_k(k∈K2)为一、二级车辆k的额定装载量;
q1_i(i∈V1_c),q2_i(i∈V2_c)为一级网络中的中转站及二级网络中客户的需求量;
[ET1_i,LT1_i],[ET2_i,LT2_i]为服务一级网络中的中转站及二级网络中客户的时间窗;
ΔT为缓冲时间;
TS1_i,TS2_i为服务一级网络中的中转站及二级网络中客户的时间;
dij为节点i,j之间的欧式距离;
tij为车辆通过节点i,j的行驶时间;
S为车辆路径中所服务的不同类型的节点集合;
|S|为节点集合中节点数量的绝对值;
p2_i为客户i的动态需求增量概率;
σ2_i-min为客户i在评估区间内历史需求量方差的最小值;
σ2_i-max为客户i在评估区间内历史需求量方差的最大值;
Δd2_i为满足客户i动态增量需求的补充量;
η为满足动态增量需求的调节参数;
paccept为启用动态需求配送概率阈值;
Dyn为动态度;
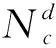
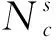
Ti,Ti+1为周期时间刻度值;
Arrays.Sort为升序排序函数;
A为时间窗跨度相对距离权重值;
d1_oi,d2_oi为第一、二级节点i到配送中心之间的距离;
y1_ik(i∈V1_c,k∈K1),y2_ik(i∈V2_c,k∈K2)为一、二级车辆开始服务节点的时间;
x1_ijk,x2_ijk为一、二级中的0-1决策变量,车辆从节点i直接行驶至节点j取值为1,否则为0;
1.2 模型构建
(1)动态需求获取准则
由于原有客户的动态需求增量与历史波动需求量之间存在一定的马尔科夫相关性,葛显龙等[2]根据这一特性,在解决客户动态需求配送问题时提出需求配额准则。该准则根据客户的历史需求水平推算当前客户的缺货概率,并通过与既定的概率阈值比较确定是否为动态需求增量补货。然而,在确定补货概率时,该文献以历史需求量方差和评估区间内最小历史方差的差值,与历史方差最大波动差值的比作为衡量指标,并未指出历史具体时刻的需求方差。为此,采用历史均值对该准则进行改进与完善,所设计的原有客户动态需求增量概率
(1)
p2_i越大表明该客户在评估的历史区间内需求量波动越大,潜在动态需求增量概率亦越大。为避免根据概率函数无差别为所有客户提供增量配送服务时对无增量需求客户的干扰,引入客户动态增量需求满足函数
(2)
基于客户动态增量需求满足函数,将对有动态增量的客户提供历史最大需求量与实际配送量的差额配送量;对无动态增量需求的,则通过概率阈值直接取消(Ti+Ti+1)/2时刻的动态配送优化,以保障初始2E-VRPTWDD优化车辆配送网络的稳定性。
(2)基于动态度的配送策略
2E-VRPTWDD中的动态度指在某一时间区间内动态客户数量与所有客户数量的比值,是制定满足动态客户需求策略的重要依据。动态度
(3)
由于客户的动态需求对配送网络的敏捷性响应提出了较高要求,为提升配送网络优化的稳定性,基于动态度高低制定两种满足动态需求的配送策略。当动态度水平较低时,在[Ti,(Ti+Ti+1)/2]配送周期内,采用配送网络局部修复策略,以尽可能降低对现有配送网络的破坏;当动态度较高时,则在(Ti+Ti+1)/2时刻启动全局更新策略,以满足新增客户和原有客户新增的需求。其中,动态度阈值决定是否启动新的车辆执行配送任务。当原有车辆装载量能够满足新增动态需求时,定义动态度为较低水平,采用局部修复策略;当原有车辆的装载量不能满足新增动态需求时,定义动态度为较高水平,采用全局更新策略。
(3)一级配送网络时间窗约束准则
一级配送网络中所服务中转站的时间与二级配送网络中所服务客户的时间之间存在相关性。因此,需基于中转站所服务客户群的最小最早开始时间与最大最晚开始时间确定中转站的时间窗约束。各中转站的时间窗约束
(ET1_i,LT1_i)=
(4)
式中:(ET1_i,LT1_i)为一级配送网络中中转站i的时间窗;ET2_iJ为二级配送网络中中转站i所服务的客户群的最早开始时间窗,LT2_iJ为二级配送网络中中转站i所服务客户群的最晚开始时间窗;ΔT为一级配送网络时间窗与二级配送网络时间窗约束存在实际意义的可连续的过渡性缓冲时间,用于保障配送车辆有足够的时间在中转站中转零部件。
(4)数学模型
层次多目标模型由一系列约束条件和多个目标函数组成,其目标是在满足约束条件的情况下,尽可能使多个目标均实现最小化或最大化[14]。本文参考文献[17-18]构建的时间依赖型车辆路径问题(Time Dependent Vehicle Routing Problem, TDVRP)模型,构建以车辆使用数量成本最小化为主要目标函数,以车辆行驶距离成本最小化为次要目标函数的层次多目标模型。在求解过程中,优先以主目标进行迭代更新求解,在主目标函数值未得到优化的情况下,再以次目标进行迭代更新求解,直至达到指定的终止条件后输出最好解。本文构建的层次多目标模型如下:
1)目标函数
(5)
(6)
2)约束条件
(7)
(8)
∀i∈V1_c,∀k∈K1;
(9)
∀i∈V2_c,∀k∈K2;
(10)
∀i∈V1_c,∀k∈K1;
(11)
∀i∈V2_c,∀k∈K2;
(12)
x1_ijk(y1_ik+TS1_i+tij)≤y1_jk,
∀i∈V1_c,∀j∈V1_c,∀k∈K1;
(13)
x2_ijk(y2_ik+TS2_i+tij)≤y2_jk,
∀i∈V2_c,∀j∈V2_c,∀k∈K2;
(14)
∀S∈V1_c,∀S≠∅;
(15)
∀S∈V2_c,∀S≠∅;
(16)
(17)
(18)
(19)
(20)
∀h∈V1_c,∀k∈K1;
(21)
∀h∈V2_c,∀k∈K2;
(22)
(23)
(24)
(25)
(26)
3)决策变量取值范围
y1_ik∈R+,∀i∈V1_c,∀k∈K1;
(27)
y2_ik∈R+,∀i∈V2_c,∀k∈K2;
(28)
x1_ijk∈{0,1},
∀i,j∈V1_c,i≠j,∀k∈K1;
(29)
x2_ijk∈{0,1},
∀i,j∈V2_c,i≠j,∀k∈K2。
(30)
其中:式(5)和式(6)分别为主目标函数和次目标函数,主目标函数为车辆使用成本最小化,次目标函数为车辆行驶距离成本最小化;式(7)和式(8)限制车辆在两级路径中的实际装载量不能超过额定装载量;式(9)~式(12)约束每级车辆为客户提供服务的时间必须在客户要求的时间窗内;式(13)和式(14)为车辆服务客户的顺序约束;式(15)和式(16)约束每级车辆行驶过程中不能形成子回路;式(17)~式(20)约束每级的每个客户均得到唯一车辆的一次服务;式(21)和式(22)约束每级车辆服务完任意客户后必须从该客户所在位置离开;式(23)~式(26)约束每级所有车辆从送配送中心出发后必须返回配送中心;式(27)~式(30)为决策变量的取值范围。
2 算法设计
因为引入客户动态需求增加了求解2E-VRPTWDD的复杂度,所以在串行模拟退火算法的基础上设计并行模拟退火算法以满足动态车辆路径问题。当动态度较低时,直接用并行算法满足修复性策略;当动态度较高时,在[Ti,(Ti+Ti+1)/2]时刻启用全局更新策略对车辆路径进行全局更新。
2.1 基于时间窗精致度的初始方案生成规则
Solomon提出推进插入启发式算法求解经典VRPTW[19],并建立了著名的Solomon测试算例库。该算法生成初始解的步骤为:选取插入成本最小的未分配路径的客户到当前的可行路径序列中,并判定插入后的路径序列是否满足车辆装载能力和时间窗约束,满足则继续插入未分配路径的客户,直至超过车辆额定装载约束为止,从而生成一条饱和可行路径序列;依次重复上述步骤,直至所有客户均被插入可行路径序列为止,生成初始方案。在选择潜在待插入客户时,有基于距离准则和基于时间准则两种选择策略。SOLOMON[20]提出基于距离准则策略,即优先选择距离物流配送中心较远的客户作为潜在备选点;CZECH等[21]则提出基于时间准则策略,即优先选择最早开始时间最小的客户作为潜在备选点。本文结合文献[17-18]提出的基于时间窗精致度策略确定潜在待插入客户,潜在客户排序函数
R(c1)=Arrays.Sort
(A×(LT1_i-ET1_i)-d1_oi)。
(31)
R(c2)=Arrays.Sort(A×
(LT2_i-ET2_i)-d2_oi)。
(32)
该式说明时间窗跨度越短、距离配送中心越远的客户排名越靠前,越会被优先考虑插入当前路径。
2.2 基于路径内外邻域搜索策略
邻域搜索指基于某种策略对原始路径进行变换产生新解的过程,按照涉及原始路径条数可分为单条路径内部邻域搜索(Or-opt和2-opt)和两条路径间的邻域搜索(2-opt*和Swap/shift)。搜索策略规则如下:
(1)Or-opt 随机选定一条可行路径上连续的若干个客户,对其在可行路径上的位置进行整体调整,从而产生新的可行路径[22]。
(2)2-opt 随机选取一条可行路径上的两个点,将第1个点之前的路径不变生成第1条新的可行路径;将第1个与第2个点之间的路径倒序后,添加到第1条新的可行路径中生成第2条新的可行路径;将第2个点之后的路径不变,添加到第2条新的可行路径中生成第3条新的可行路径;最终以目标函数值为评价准则,保留4条可行路径中最优的一条路径作为当前的最优可行解[23]。
(3)2-opt*将两条可行路径上分别被某一节点切断的滞后连续路径段互换位置,产生两条新的可行路径[24]。
(4)Swap/shift 将两条可行路径的两个节点互换或单向插入,产生两条新的可行路径[25]。
基于路径内外邻域的4种搜索策略如图2所示。在设计搜索策略过程中,这4种策略被选择的概率均设定为1/4。具体实现过程为随机产生一个[0,1]内的随机数,若该随机数的取值落在[0,0.25),则选择Or-opt进行邻域搜索;若随机数取值落在[0.75,1),则选择Swap/shift进行邻域搜索,更新当前可行路径。

2.3 并行模拟退火优化设计
1983年,KIRKPATRICK等[26]为解决局部最优解的问题提出模拟退火算法,算法核心思想是在1953年Metropolis提出Metropolis准则的基础上融合了退火过程。物体温度越高,其内部的分子和原子状态越不稳定,温度越低,其内部的分子和原子状态越稳定,模拟退火算法正是通过模拟这一过程来寻找原子状态相对稳定的局部最优解。在退火过程中,通过Metropolis概率接受准则来迫使算法跳出局部最优解,进而寻找全局最优解,其策略为:在迭代过程中,如果系统整体能量梯度下降,则将状态的转移概率设定为1;如果迭代过程中系统整体能量梯度上升,则状态转移能否被接受取决于在[0,1]内产生的随机数,以及与能量和温度相关的动态概率大小的关系,如果小于该动态概率,则这种状态转移被接受,否则被拒绝。这一过程有效地使算法迭代过程跳出局部最优解,继续迭代寻找下一个新的局部最优解。随着温度的不断下降以及上述迭代过程的不断重复,会产生若干局部最优解,最终通过适应度函数值挑选出所有局部最优解中的全局最好解。串行模拟退火算法的伪代码如下:
Pseudo code of serial simulated annealing algorithm
1.Start
2.Set x=0 and T=m
3.Public static void main(create new(y(x)))
4.i=random.randint(0,len(y(x)-1))
5.j=random.randint(0,len(y(x)-1))
6.y(x)[i],y(x)[j]=y(x)[j],y(x)[i]
7.Return y(x)
8.While(T>T-min)
9.{ Cost savings=f(y(x+1))-f(y(x))
10. if(Cost savings≥0)
11. y(x+1)=y(x)
12. else
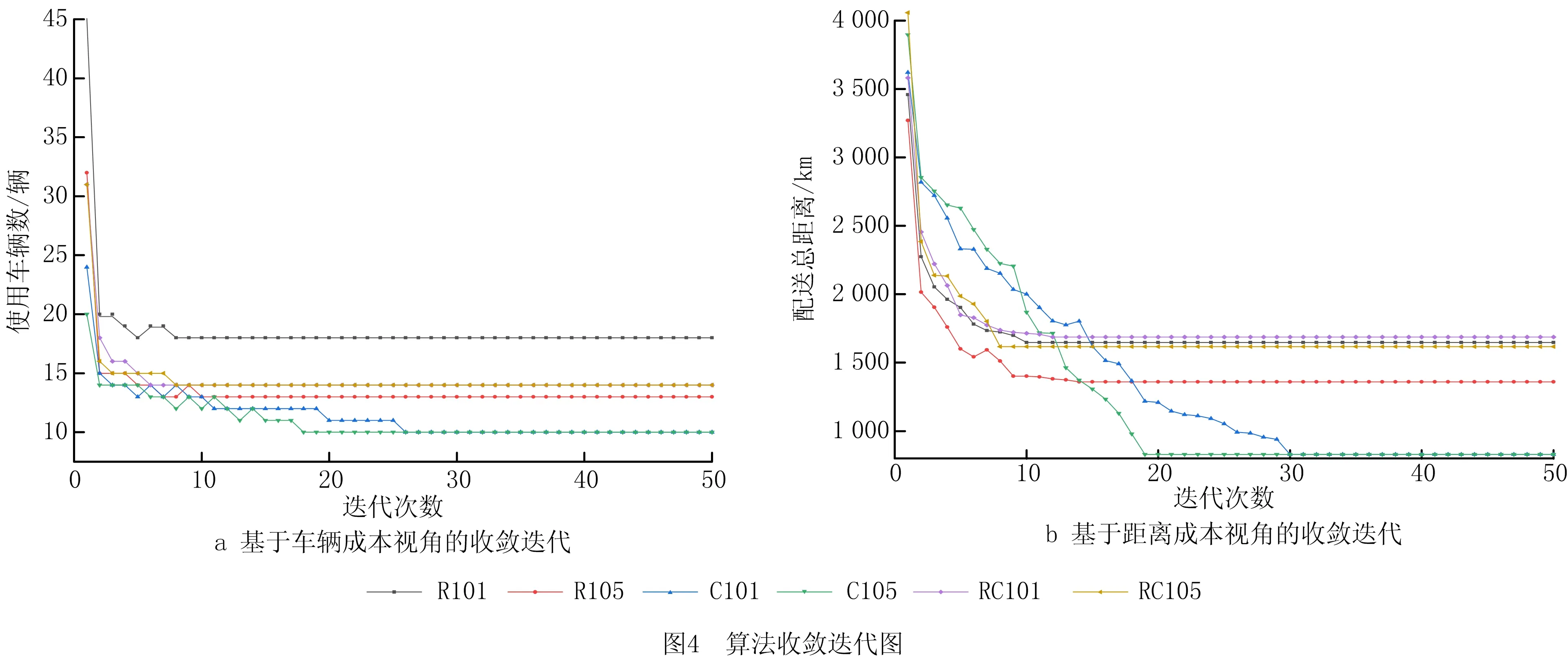
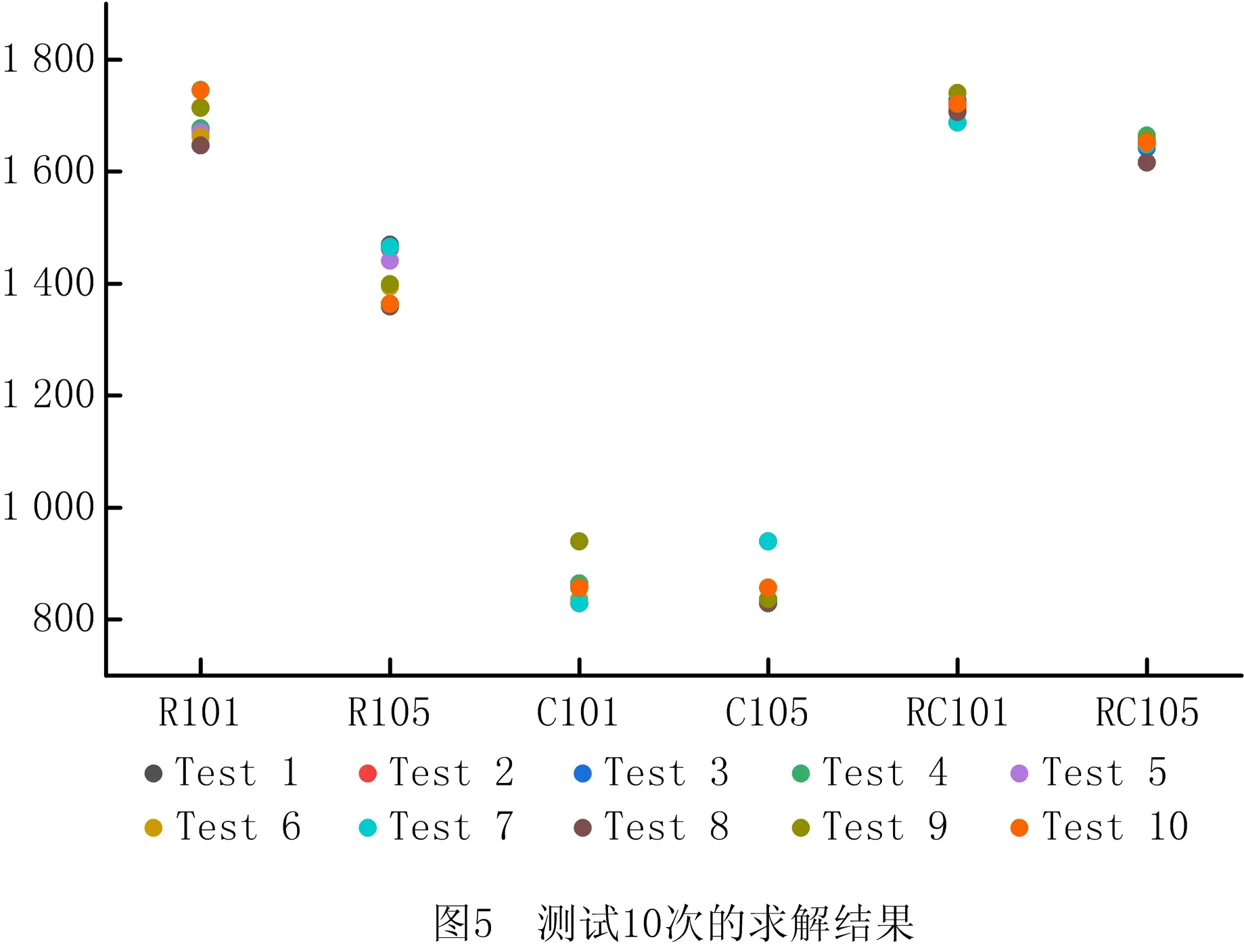
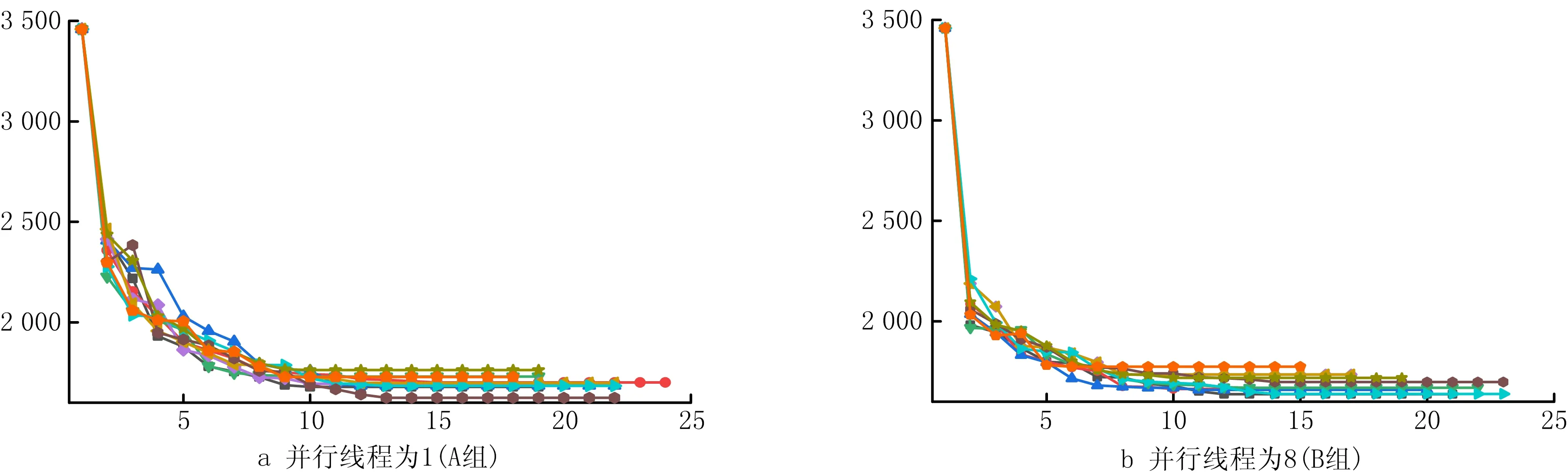
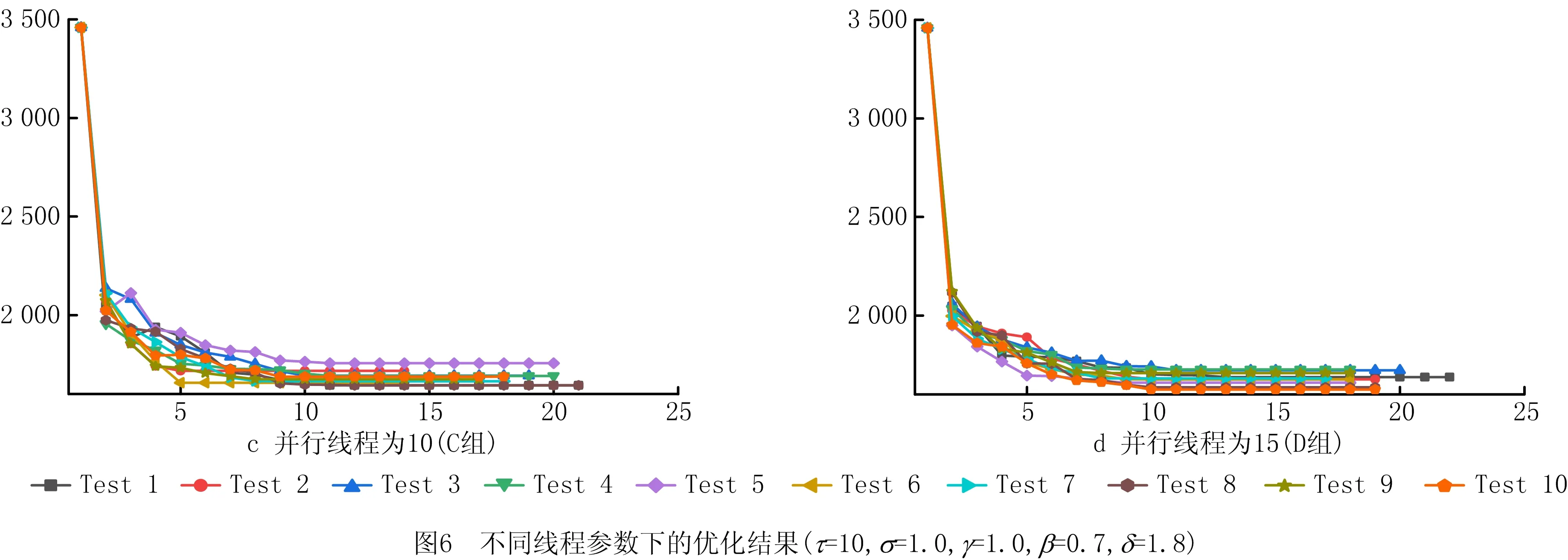
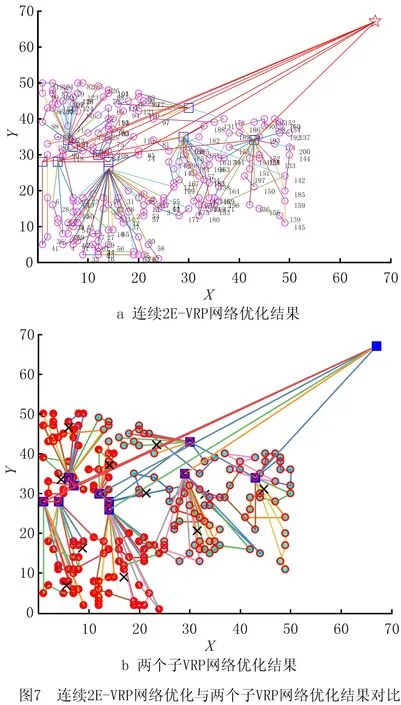
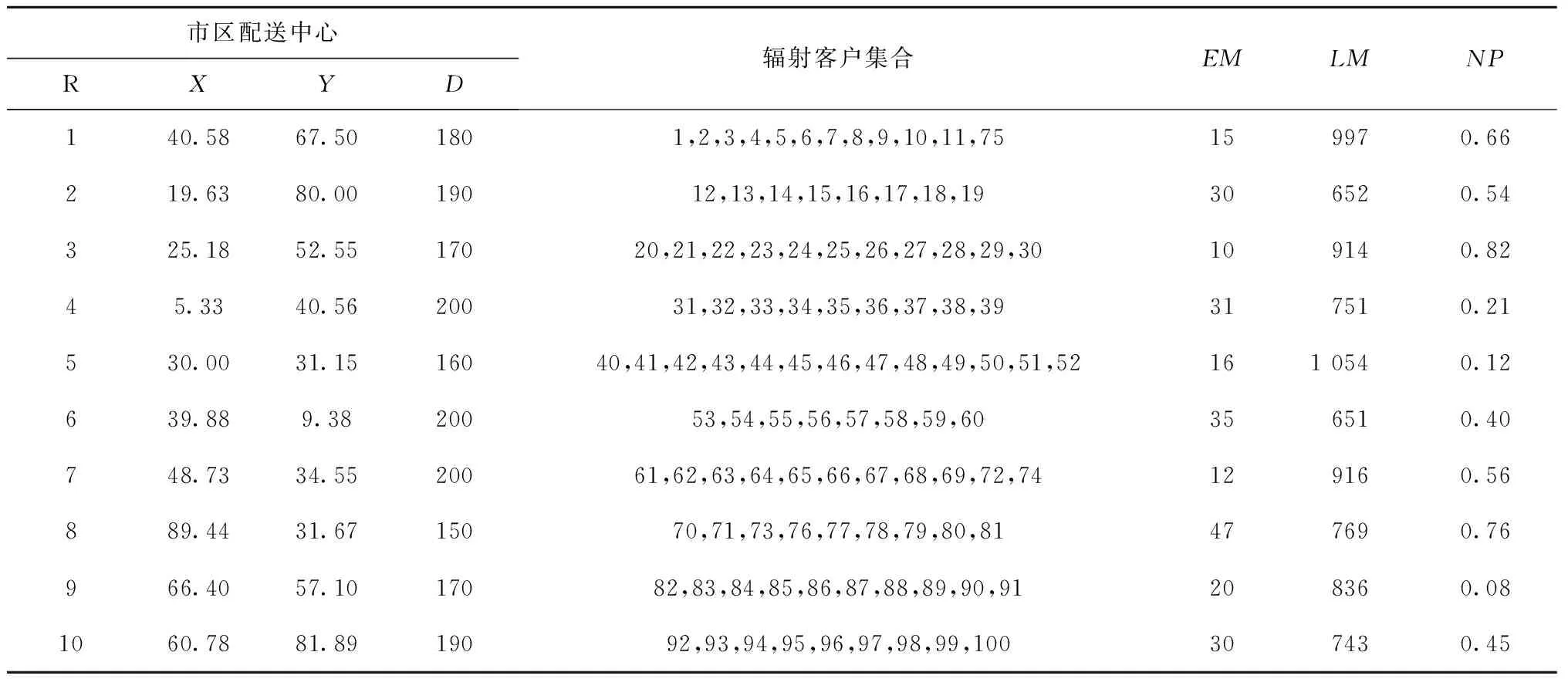
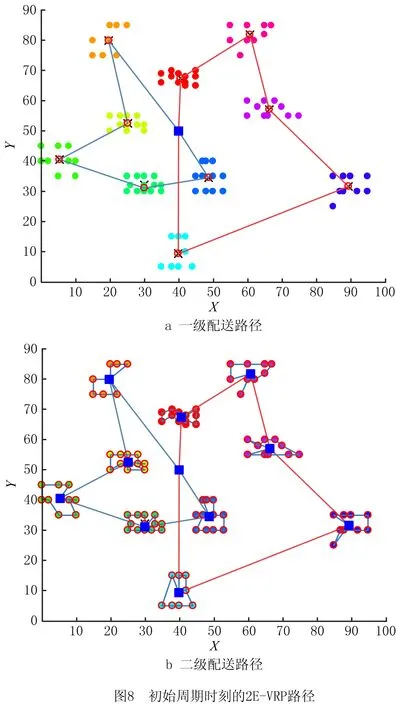
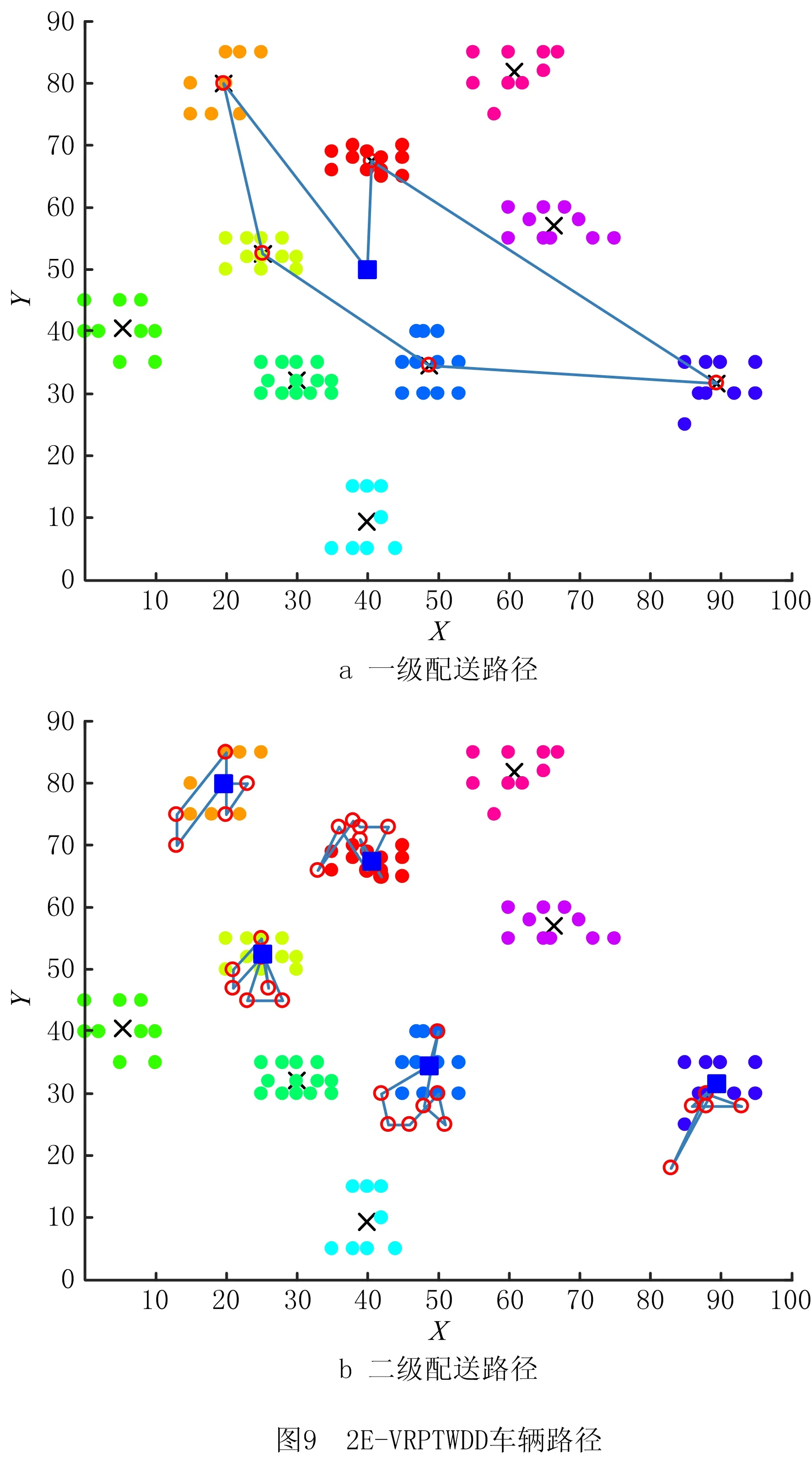
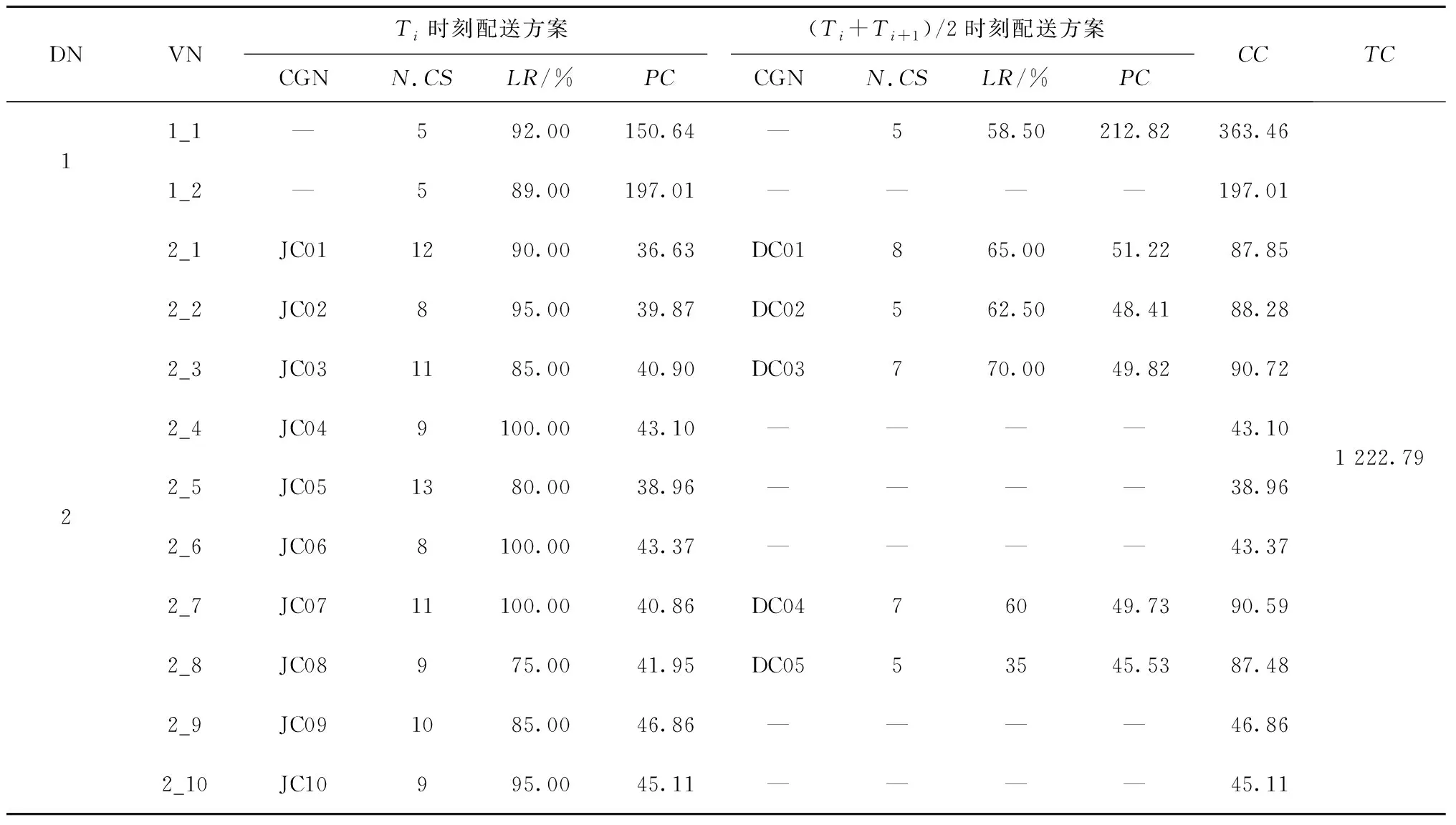
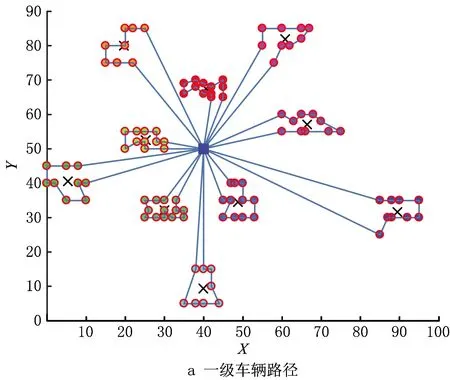
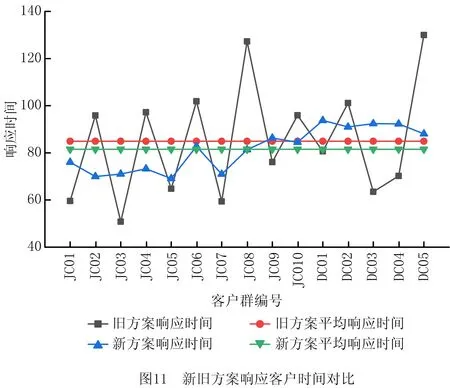
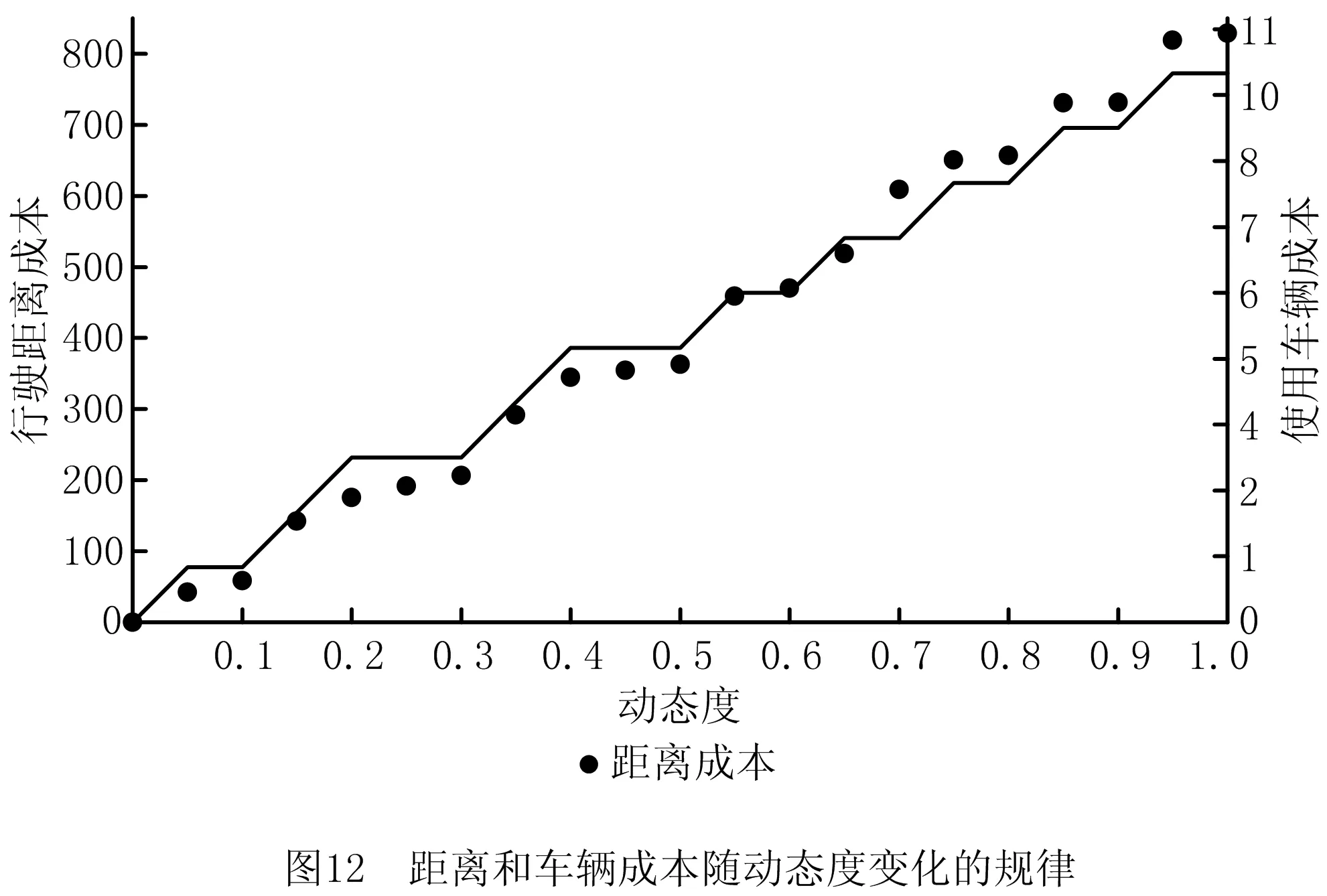
13.{ If(random(0,1) 14. y(x+1)=y(x) } 15.x=x+1 16.T=r*T } 17.End 18.Output optimal solution and related parameters 其中:f(x)为系统在x状态下的目标函数值;y(x)为系统在x时所处的状态;y(x+1)为系统在x之后所处的状态;r为温度下降速度调节参数;T为系统整体的温度值;T-min为算法终止的温度下限值。模拟退火算法的求解质量受初始温度和降温速率影响较大,高的初始温度与缓慢的降温速率有利于寻找到全局最好解,然而需要花费大量的计算时间。为此,有学者将并行移动、多马尔科夫链融入模拟退火过程以实现算法的并行化计算[5],其核心思想是将一条马尔科夫链分裂为在一定时间、空间内既能相互独立生长又能彼此交互信息的多条马尔科夫链。马尔科夫的决策策略可分为同步和异步两种策略,基于马尔科夫异步策略的并行模拟退火算法,实际上是将计算均匀分布到不同的线程上,各个线程独立运行模拟退火算法,当各线程运行结束时,相互对比并选择较优的局部最优解更替当前阶段的全局最好解。考虑到求解效率与动态度的关系,基于马尔科夫同步策略所设计的用于求解2E-VRPTWDD的并行模拟退火算法流程如图3所示。 在基于马尔科夫同步策略的并行模拟退火算法中,嵌入向前插入启发式(Push Forward Insertion Heuristic,PFIH)算法,在初始阶段,由主线程向各个分线程传输一个基于时间窗精致度的初始解{x1,x2,…,xn},随后各个分线程开始独立运行一个以Metropolis接受准则为主的过程,当经过一个固定的路径寻优周期后,各个分线程单向传递并比较彼此Metropolis接受准则下得到的局部最好解{f(x1),f(x2),…,f(xn)},选择最小值作为分线程下一次迭代的初始解。各分线程运行结束后,将彼此得到的局部最好解传递到主线程,按照接近最优解的程度重置各初始解{x1,x2,…,xn},并将其循环输入各个分线程,以实现并行运算。其中,所设计的并行模拟退火算法伪代码如下: Pseudo code of parallel simulated annealing algorithm 1.Set T=m and r=r0 2.Generate initial solution{x1,x2,…,xi} based on PFIH 3.Send {x1,x2,…,xi} to thread {p1,p2,…,pi} 4.For 1:pi 5.Public static void main (create new(y(x))) 6.Char a=random. randint (0,1) 7.Switch (a) 8. Case '0.00≤a<0.25' 9. System.out.printIn (initial solution xi+1based on Or-opt strategy) 10. Break; 11.Case '0.25≤a<0.50' 12. System.out.printIn (initial solution xi+1based on 2-opt strategy) 13. Break;…; 14. Return y(xi+1) 15.While(T>T-min) 16.{ Cost savings=f(y(xi+1))-f(y(xi)) 17. If (Cost savings≥0) 18. y(xi+1)=y(xi) 19. else 20.{ If (random (0,1) 21. y(xi+1)=y(xi) } 22.xi=xi+1 23.T=r*T } 24.End 25.System.out.printIn (Update initial solution{x1,x2,…,xi}) 26.Choose min{f(y(x1),f(y(x2),…,f(y(xi)} as the current optimal solution 27.If go=false and stop, else continue; 28.Send update {x1,x2,…,xi} to thread{p1,p2,…,pi}… 29.End loop 30.Output optimal solution and related parameters PERBOLI等[27]研究了2E-VRP,并公布用于对该问题进行测试的set2~set5不同系列的基准数据(https://www.univie.ac.at/prolog/research/TwoEVRP)。 然而,在PERBOLI研究的2E-VRP中,每个中转站可以跨区域为所有客户提供配送服务且没有时间窗约束。在实际运营中,考虑到配送员对区域的熟悉度,以及对不确定事件的处理能力,企业主管通常会安排最佳配送员负责固定区域内的配送。因此,不采用PERBOLI给出的2E-VRP数据作为测试基准数据。另外,本文研究的2E-VRPTWDD属于两个带时间窗的车辆路径联合优化问题,但目前还没有相关的测试算例。 因此,选取SOLOMON[20]在1987年给出的带时间窗的车辆路径R,C,RC系列测试数据,作为进一步验证所设计模型和算法的基准数据,数据下载网址为http://web.cba.neu.edu/~msolomon/。R系列包括R101~R112,且每个测试集的100个客户与一个配送中心呈现随机特征,分布在100×100的坐标系内;C系列包括C101~C109,且每个测试集的100个客户与一个配送中心呈现聚类特征,随机分布在100×100的坐标系内;RC系列包括RC101~RC108,且每个测试集的100个客户与一个配送中心呈现聚类与随机混合特征,分布在100×100的坐标系内。测试环境参数为MacBook Air 13.3 Core i5,1.8 GHz CPU双核,8 G内存,128 G SSD;Windows 10 64 bit;Java JDK-8u251编程环境。算法基本参数包括并行线程数量为6,连续未能找到相对局部改进解的算法终止次数为10,温度下降系数为0.8,温度与成本比例系数为1;选择R101,R105,C101,C105,RC101,C105作为对比实例。计算结果与当前已知最好解及文献[28]的计算结果对比如表1所示。 表1 与已知最好解及文献[28]优化结果的对比 由表1可知,本文设计的并行模拟退火算法在寻优能力上,明显整体优于文献[28]设计的分散搜索算法。所求的R105最好解相比已知最好解的优化率达到1.31%,使用的车辆数由Solomon给出的已知最好解的14辆降低到13辆。所求的R105的最优路径所需的13辆车的行驶路径分别为:1 48 37 20 9 85 18 61 90 1;1 60 93 99 100 88 58 44 97 1;1 34 66 72 10 82 4 69 55 25 81 1;1 64 63 12 65 50 47 49 1;1 22 74 76 42 23 75 59 1;1 73 40 24 68 57 5 56 26 1;1 53 83 8 91 11 51 2 1;1 96 15 45 39 87 92 101 94 1;1 32 89 19 7 95 1;1 29 13 30 80 79 35 36 78 1;1 43 16 3 41 54 27 1;1 28 70 77 31 52 21 67 33 71 1;1 6 84 46 62 17 86 38 98 14 1。其中,采用并行模拟退火算法优化过程中,主目标函数和次目标函数的迭代收敛图如图4所示。结果表明,所设计的算法能够较快地收敛到相对较优解,较好地满足VRPTW优化的需要。 为进一步测试算法的稳定性,在相同的参数配置下,对R101,R105,C101,C105,RC101,RC105分别测试10次,结果如图5所示。 图5为运行10次的结果,在10次测试过程中,R101的最大值为1 746.37,最小值为1 646.73,平均值为1 689.69,而已知最好解为1 645.79,相对已知最好解的平均误差率为2.67%。R105的最大值为1 469.01,最小值为1 359.32,平均值为1 407.76,而已知最好解为1 377.11,相对已知最好解的平均误差率为2.23%。6个测试集中相对已知最好解的平均误差率最大为C105(4.85%),最小为RC105(0.95%)。总而言之,本文算法均能找到相比已知最好解较好的解,由于启发式算法的局限性导致每次求解结果均有一定波动,而10次测试的相对平均误差率均控制在5%的可接受范围内,且在10次内基本能够求得与已知最好解接近甚至更优的解,说明所设计的算法具有一定的稳定性,能够用于求解2E-DVRPTWDD。 为分析Or-opt,2-opt,2-opt*,Swap/shift 4种邻域操作算子对算法改进的效果,在不同组合下,分别对算法运行10次,结果表明,融合Or-opt,2-opt,2-opt*,Swap/shift 4种邻域操作算子能有效提升算法性能,主要原因在于不同的邻域操作策略代表不同的新解生成规则,通过生成随机数的方式随机选择4种邻域策略时,能够有效扩大可行解的搜索范围,有利于在搜索空间内寻找到相对更好的解。相反,当采用单一邻域策略时,由于邻域搜索操作规则的一致性,容易导致算法陷入局部最优解,不利于在更大的空间范围内搜索到相对更好的解。为进一步探索并行数量对优化结果的影响,通过采用控制变量法的方式设置不同的实验组,分别对其进行测试实验,具体实验组的设置规则为:在其他参数保持不变的情况下(τ=10,σ=1.0,γ=1.0,β=0.7,δ=1.8),将并行线程数量分别设置为1,8,10,15,分别对应A,B,C,D 4个相互对照的实验组,每个实验组单独运行10次,统计每次运行所得的车辆行驶距离成本和车辆使用数量成本。 就实例R101的求解结果而言,10次测试均能找到优于或与已知最好解接近的解,R101已知最好解中的车辆行驶距离成本为1 645.79,车辆使用成本为19;所找到的最好解中的车辆行驶距离成本为1 624.15,相比已知最好解的优化率为1.31%;车辆使用数量成本为18,相比已知最好解的优化率为5.26%。在4组实验组中,性能表现最好的是D组,10次测试的车辆行驶距离成本平均值为1 679.72,车辆使用数量成本为18。表明随着并行线程数量的增加,算法的表现性能趋于良好。不同线程数对优化迭代过程的影响如图6所示,图中横坐标表示算法外层迭代步长,纵坐标表示车辆的行驶距离成本。 图6反映了在不同线程参数设置下,不同测试实验中的迭代收敛过程。在不同的并行线程设置下,起始位置均相同,表明初始解的生成只与初始解的构造规则有关,与并行线程数量多少无关。在求解R101时,初始解中的车辆行驶距离成本均为3 458.79,车辆使用数量成本均为48。在10次邻域内搜索不到更优解便终止算法的条件设置下,4组实验的解趋于稳定的平均迭代步长分别为11.6,10.6,9.2,9.8,表明并行数量对算法达到稳定状态的速度有一定影响,当并行数为10时,平均迭代步长最小,为9.2步。然而,随着并行数量的增加,算法达到稳定状态的耗时也会增加,从而增加了寻得相对最优解的时间成本,这是因为并行线程数量会占用更多内存,并进行更多的内部循环迭代。当并行线程设置为1时,平均耗时为90 s左右,而当并行线程数量设置为15时,平均耗时为300 s左右。接下来,以Perboli给出的2E-VRP中的2eVRP_200-10-3实例为基准数据,对比分析连续两级网络优化和两个子网络优化的结果,如图7所示,该实例包括200个客户和10个中转站。 其中,图7a为采用连续2E-VRP优化方法得到的优化结果,车辆行驶距离成本为2 142.36,在一级配送网络中共需4辆车执行配送任务,在二级配送网络中共需52辆车执行配送任务。图7b为两个子网络的优化结果,即首先根据配送员对区域的熟悉度对200个节点进行聚类,以确定中转站的位置,构建由配送中心和中转站节点组成的一级配送网络;其次,构建由各中转站与客户组成的二级配送网络。优化结果显示,虽然采用连续2E-VRP优化方法在车辆成本方面具有优势,但是由于在优化过程中忽略了配送员对配送区域的熟悉度,导致出现跨区域配送,进一步降低了配送效率;当采用两个子网络的优化方法时,虽然车辆行驶距离成本略高于连续2E-VRP结果,但是能够满足配送员对配送区域熟悉度的要求。因此,将连续2E-VRP优化问题转换为两个VRP的优化问题,在提升配送效率方面具有现实意义。 H公司作为一家服务于集成制造产业群的供应商,为上百个不同的客户提供各种零部件的供应服务,各大客户由于市场追加订单、原有零部件供应中途故障等不确定因素的影响,会不定时地向公司发出紧急供应订单需求以确保主生产线稳定运行。 现选取某一周期内公司服务的100个静态客户和32个动态客户为案例进行研究。鉴于可比较性,使用Solomon给出的C101中的100个客户坐标、需求、时间窗和服务时间数据表示公司服务的客户,对比分析公司采用的新方法和原有方法的效果,10个二级配送中心和100个静态客户的地理分布与需求如表2所示。 表2 静态客户与所属中转站及配送中心信息 公司在确定中转时,考虑到配送员对区域的熟悉度,会采用聚类方法确定一个能够辐射固定区域客户的中转站。受中、重型车辆通行的限制,在一级配送网络中使用核定装载量为10 t的送货车,在二级配送网络中使用核定装载量为2 t的卡车。在制定满足动态客户的车辆行驶路径优化方案时,采用文献[29]给出的动态客户满足方法,即将完整的一个物流配送周期划分为两部分,在1/2周期时刻启动满足客户动态需求的配送策略,以满足前半周期内的新增客户和新增需求量。执行物流配送任务过程中的基本参数如表3所示。 表3 执行物流配送任务过程中的基本参数 根据新增概率和接受动态新增概率阈值规则确定在[Ti,(Ti+Ti+1)/2]区间内服务的5个动态客户和未被服务的静态客户。在[Ti,(Ti+Ti+1)/2]时期内新增客户的数据如表4所示。 表4 在[Ti,(Ti+Ti+1)/2]时期新增的客户数据 在初始化带时间约束的2E-VRP优化过程中,仅考虑对应一个配送周期[Ti,Ti+1]的静态客户。采用所设计的模型和算法,得到的初始周期的最好2E-VRP路径如图8所示。 一级物流配送网络中,共调用了两辆额定装载量为10 t的货车为市区物流配送中心配送货物,车辆1的配送路线为0→2→3→4→5→7→0,车辆2的配送路线为0→6→8→9→10→1→0。两辆车的装载率分别达到92%,89%,说明车辆的额定装载量得到了较充分的利用,为车辆预留一定空间也符合实际情况。根据接受满足动态新增概率阈值为0.5可知1,2,3,7,8存在动态客户。假定新增客户动态度为0.5,原有客户新增需求动态度为0.2,则根据式(3)生成[Ti,(Ti+Ti+1)/2]内的新增动态客户数量如表5所示。 表5 新增动态客户数量 在满足新增动态客户需求阶段,共服务5个中转站的24个新增客户和8个原有客户追加需求变成的新客户,新增动态客户用空心圆表示,在(Ti+Ti+1)/2时刻优化得到的2E-VRPTWDD车辆路径如图9所示。 表6所示为2E-VRPTWDD配送模式下的装载率、服务客户数和路径成本。在设定2E-VRP网络中车辆额定装载量不变的情况下,由于动态度的约束关系,使得(Ti+Ti+1)/2时刻满足动态客户的车辆装载率明显低于Ti时刻满足静态客户车辆的装载率,在一定程度上造成车载浪费。因此,实际应用场景中,在满足动态客户需求时可考虑采用多车型配送模式,以减少车辆装载的浪费。 表6 2E-VRPTWDD配送模式下的装载率及路径对比 受道路交通的限制,公司在原有送货方案中使用额定装载量为2 t的卡车为100个静态客户和32个动态客户提供零部件供应服务。在一个配送周期[Ti,Ti+1]的起点,公司以行驶成本和车辆使用成本最小化为目标,调用10辆车分别为100个客户提供供货服务,其车辆行驶成本为828.94 km。在(Ti+Ti+1)/2时刻调用5辆车为32个动态客户提供零部件供货服务,其车辆行驶成本为445.47 km。公司原有的两级车辆行驶路径优化如图10所示。 表7所示为采用原有方案时的车辆装载率和路径成本。就总成本而言,所设计的2E-VRP路径成本为1 222.79,略优于H公司原有的1 274.41。原有配送方案中各路径上的车辆装载率与所设计的2E-VRPTWDD模式下各路径车辆装载率保持一致,这是因为这一过程中均使用装载量为2 t的车辆为相同的客户群提供服务,但就各路径的车辆行驶成本而言,所设计的2E-VRPTWDD模式下的路径成本均值要优于原始方案。 表7 原有2E-VRP网络装载率及路径对比 响应并满足客户的需求时间是衡量供应商运营效率的重要指标之一,下面从响应时间的角度对新旧方案进行对比分析。假设新旧方案中车辆的行驶速度均相同且均为单位行驶速度,车辆从配送中心驶出,服务完对应的客户再返回配送中心记为一个响应满足客户时间,当一级配送网络中的10 t大货车服务多个客户群时,取其平均值作为响应满足各客户的时间。新旧方案的响应客户时间如图11所示。 由图11可知,新方案的平均响应时间略优于旧方案,说明所设计的方法能够较好地满足动态客户的快速需求,进一步表明所设计的方法能够满足供应商对客户动态需求的响应。另外,新方案响应时间的波动程度优于旧方案,说明所设计的方法具有较强的稳定性。本节将分析动态度对车辆行驶距离成本和车辆使用数量成本的影响,将动态度设置为由0开始,每次增加0.05个单位动态度,直到1结束的20个梯度,每个梯度下运行10次取最优的距离和车辆成本作为最终成本,得到的距离和车辆成本随动态度变化的规律如图12所示。 图12显示,距离和车辆成本总体随动态度的增加而增加,主要原因是当客户数量和需求量增加时,公司需要安排更多车辆为增量客户提供配送服务,这一现象与实际情况相符。车辆使用成本随动态度的增加而呈现出阶段性增加的特征,例如:动态度在0.55~0.65之间的车辆使用成本均为6,在0.65~0.70之间的车辆使用成本均为7,即动态度在一定范围内变化并不会增加车辆使用数量成本,进一步表明所设计的方法具有良好的鲁棒性,其原因是当动态客户新增需求量在未超过现有车辆运力时,现有车辆有能力为动态客户提供配送服务,而不需要重新启动新的车辆。因此,在局部动态度变化过程中,动态度与车辆数量使用成本无关。 在各大城市陆续实施中、重型货车限行政策的背景下,2E-VRP受到重视,而在车辆执行任务过程中,客户存在动态需求的不确定性,企业是否及时响应客户的动态需求对于能否提升客户满意度和运营效率非常重要。当企业接受客户的动态需求变更后,原有车辆路径方案可能难以满足新客户的订单需求,因此制定合适的响应客户动态需求的策略并及时更新车辆路径,对企业的重要性不言而喻。为此,本文针对配送环节中客户动态需求的不确定性,以及配送时间个性化导致的动态配送网络响应不及时等现实问题,设计基于客户动态增量概率阈值和动态度响应增量需求的优化路径更新策略,构建了以车辆使用成本和距离成本最小化为主、次优化目标的2E-VRPTWDD数学模型,并设计了改进的并行模拟退火算法,旨在为考虑动态客户需求的2E-VRP优化提供方法与理论支撑。通过本文研究得到的结论如下: (1)引入客户动态增量需求满足函数和动态度衡量指标,能够有效降低动态配送网络在空间与时间维度的求解复杂度。 (2)相比SOLOMON算例中R105的已知最好解,优化率达到1.31%,说明所设计的并行模拟退火算法在求解质量方面具有一定优势。 (3)通过对比分析新旧方案可知,2E-VRPTWDD模式下的车辆调度方案对提升供应商响应客户需求速度有积极的作用。 (4)通过分析动态度大小对优化结果的敏感性可知,车辆调度方案在局部动态度变化范围内具有较强的鲁棒性,总之,车辆使用成本与距离成本随着动态度的增加而增加。 然而,车辆的装载率在满足客户动态增量需求配送阶段普遍偏低,说明在无差异车辆配置的情况下存在车辆装载浪费,而现实中的物流配送企业通常配备无差异的车辆。因此,下一阶段将对多种车型灵活组合的动态配送问题展开研究,以进一步探索多车型的最优组合配送策略,为物流企业减少装载浪费提供科学的指导。
3 算法性能测试

4 案例研究

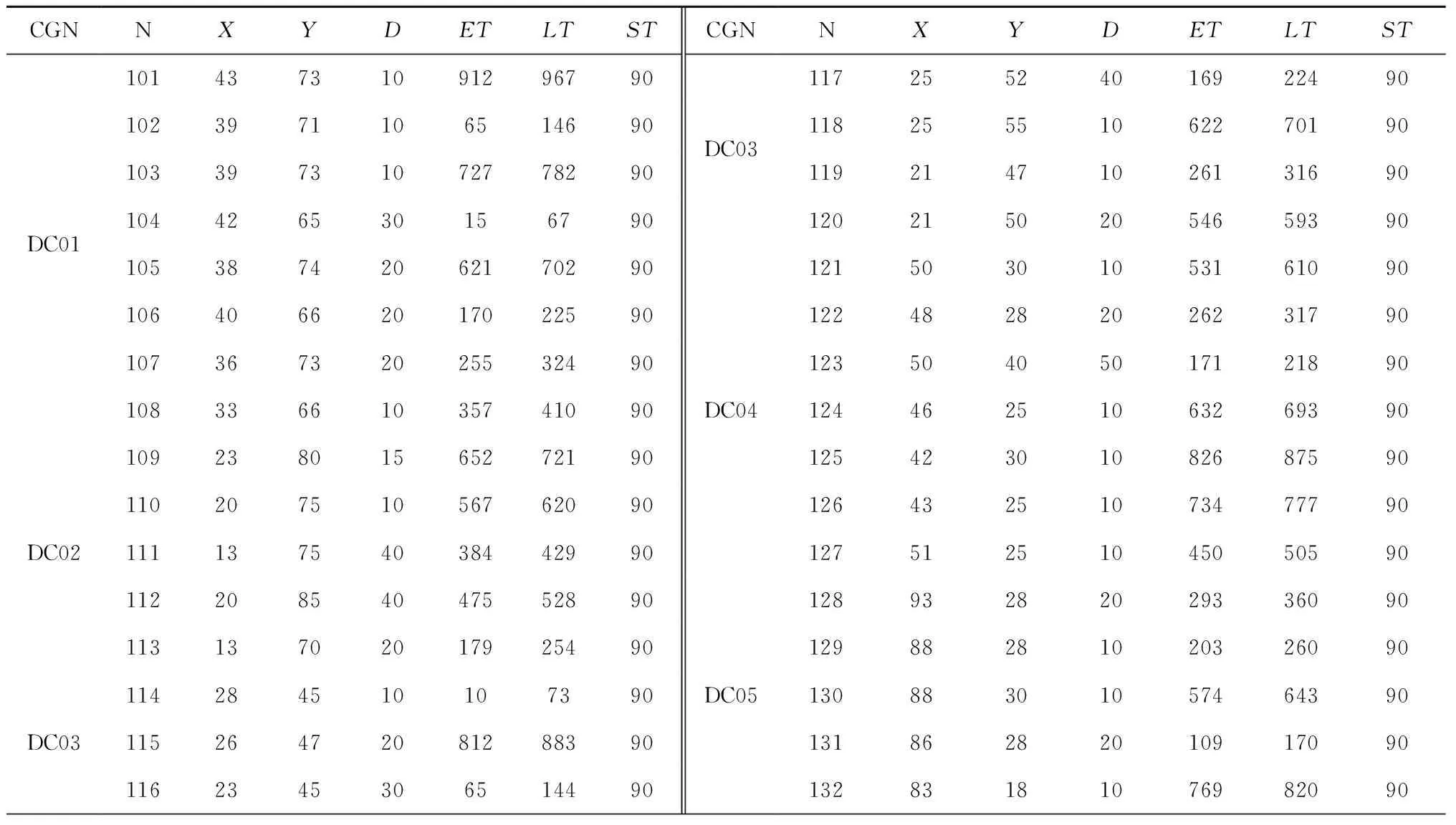
4.1 考虑动态度和时间窗的两级车辆路径优化

4.2 新旧方案对比及敏感性分析


5 结束语
