一类基于心理作用的随机SIRS传染病模型

王定宇, 周少波

(1.华中科技大学数学与统计学院, 湖北武汉 430074;2.密歇根大学统计学系, 密歇根安娜堡 48104)

1.引言

长期以来传染病的传播和流行给人类健康带来了极大威胁, 例如曾在中世纪流行于欧洲的黑死病, 如今的新型冠状病毒肺炎等, 都对人类的健康和经济的发展带来了负面的影响.为研究1665-1666年的黑死病在英国伦敦的流行规律以及1906年瘟疫在印度孟买的流行规律,Kermack和McKendrick在1927年首先建立了SIR仓室传染病模型[1].他们的工作为SIR模型的建立奠定了基础.SIRS和SEIR等传染病模型都是在SIR模型的基础上提出来的.SIR模型的具体数学表达形式如下

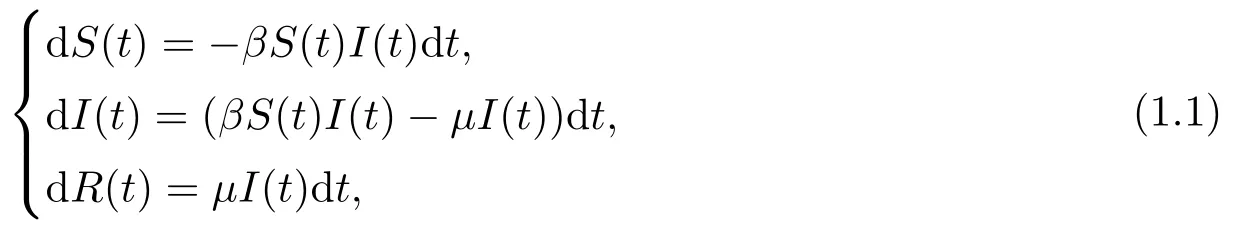
其中S(t)表示易感者(Susceptible), I(t)表示患病者(Infectious), R(t)表示康复者(Recovered),β表示日接触率, µ表示日恢复率.

由于人类对某些疾病的免疫时间是有限的, 若考虑康复者会重新转换成易感者丧失免疫力, 人们提出了如下SIRS模型

其中γ表示丧失免疫率.

由于现代人对疾病防控意识的增强, 心理作用在传染病治愈过程中的作用越来越明显.同时在绝大多数传染病模型动力学分析的文献中, 都只考虑了系统内总人口恒定的特殊情况.因此朱晶[2]假定系统内总人口的增长符合Logistic人口增长模型, 提出了如下基于心理作用的SIR传染病模型

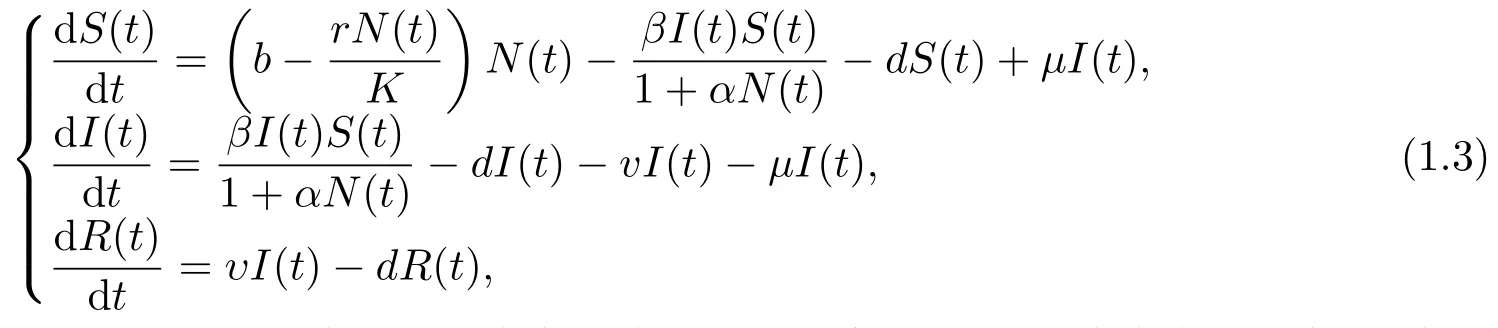
其中N(t)为t时刻的人口总量; b为自然出生率; d为自然死亡率; r =b −d为内禀增长率; K为环境容纳量; α为心理作用系数(即采取相应的预防控制措施影响发病率), 且假设1/K < α < 1;β为传染率; µ为自然恢复率; υ为获得终身免疫率.除内禀增长率r以外的所有参数均为正常数,参数r的大小由自然出生率b和自然死亡率d共同决定.证明了当阈值<1时, 疾病将会消亡;当阈值>1时, 疾病将会持久存在.

显然, 在模型(1.3)中, 当心理作用系数α的数值相对较大时, 单位时间内由易感者转换成感染者的人数会降低, 传染病的传染将会得到抑制; 当α的数值较小时, 单位时间内会有更多的易感者转换成感染者, 则传染病的传染趋势将会扩大.因此, 心理作用系数α将会对疾病的传播趋势产生深刻的影响.

基于此, 李文轩等人[3−5]提出了人口增长满足Logistic方程的基于心理作用的SIRS模型

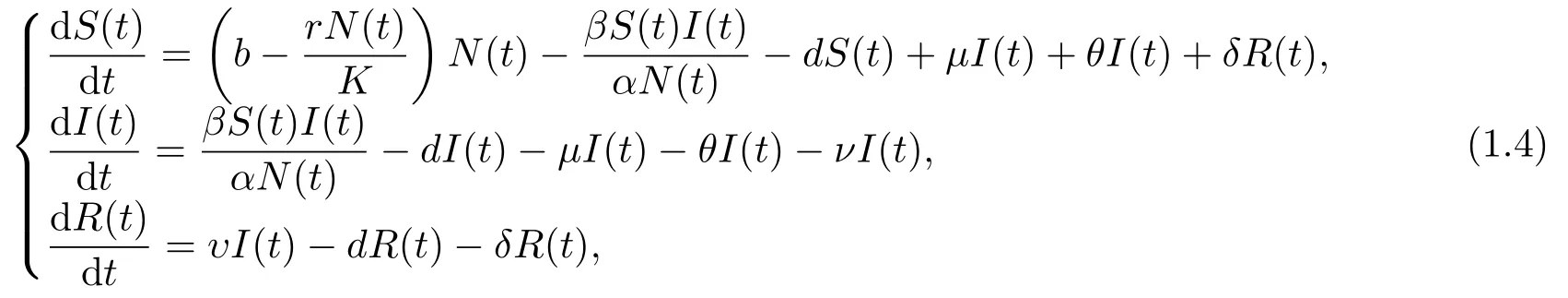
其中θ表示治愈率; δ表示丧失免疫率; υ表示获得暂时免疫率.

实际上, 我们在进行参数估计(如β)时会不可避免的存在一些误差, 即参数β的估计通常是“均值”+“误差项”, 若假定误差项服从正态分布, 并将其标准偏差看作是噪声强度, 且该噪声强度可能依赖于易感人群S(t)及染病人群I(t), 则β可由β+σ ˙ B(t)替代, σ >0代表噪声强度,=dB(t)/dt为白噪声(即B(t)是布朗运动).因而(1.4)相应的随机扰动模型为

将模型(1.5)中的三个方程相加有

因此模型中的总人口增长满足Logistic方程.

近些年来, 许多学者研究了类似的随机扰动传染病模型[6−7].杜金姬等[6]研究了一类具有logistic增长的随机SIRS传染病模型, 证明了模型具有唯一的全局正解并指出模型的正解是稳定的马尔可夫过程, 同时也给出使模型中疾病灭绝的充分条件.朱玲等[7]建立了一类具有Logistic增长的随机SIVR传染病模型, 证明了随机系统正解的存在唯一性, 讨论了随机模型的解在与其对应的确定性模型的无病平衡点附近的渐近行为, 并指出白噪声强度σi对随机系统的影响, 认为易感者人数变化所受到随机扰动的强度σ1会对整个随机系统产生决定性的作用.

本文将通过构造Lyapunov函数, 利用Itˆo引理, 强大数定理和停时等随机分析理论证明模型(1.5)全局正解的存在唯一性, 并给出使疾病灭绝和持久的充分条件.其次, 本文将考虑时滞对系统(1.5)的影响, 证明基于心理作用的时滞随机SIRS传染病模型全局正解的存在唯一性.最后将应用Euler方法和Milstein方法进行数值模拟, 验证本文建立的结论并进行分析.

2.基于心理作用的随机SIRS传染病模型

进而

令k →∞, 有∞> V(S(0),I(0),R(0))+AT = ∞.由此出现矛盾, 假设不成立.因此有τ∞=∞ a.s., 从而τe=∞ a.s.证毕.

Ⅱ 灭绝性

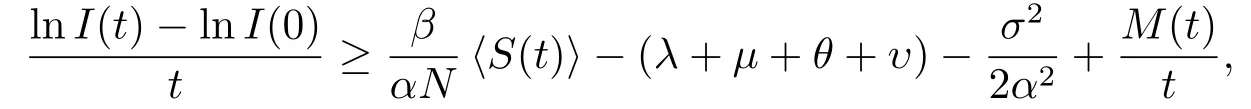
其中

于是

其中ηj是相互独立且服从标准正态分布N(0,1)的随机变量.

相应的, 系统(1.5)对应的Milstein高阶近似解Sj,Ij,Rj满足如下方程组:

其中ξj是相互独立且服从标准正态分布N(0,1)的随机变量.

若取初始时刻易感者人数250万人, 感染者人数150万人, 免疫者人数5万人, 即S(0) =250,I(0) = 150,R(0) = 5; 取传染率β = 0.05, 自然出生率b = 0.5, 环境容纳量K = 500, 心理作用系数α = 0.1, 自然死亡率d = 0.2, 自然恢复率µ = 0.05, 治愈率θ = 0.2, 丧失免疫率δ =0.01, 获得暂时免疫率υ =0.1, 随机扰动σ =0.02.由于

−0.001=2α[β −α(d+µ+θ+υ)]<σ2=0.004<βα=0.005,

因此在该参数下系统存在唯一的全局正解且满足定理2.2的条件.又由定理2.2易得−0.07 < 0 a.s.故疾病最终将会以指数形式灭亡.同时通过计算可得= 0.873 < 1.图1中数值模拟的结果映证了此时疾病将会灭绝.

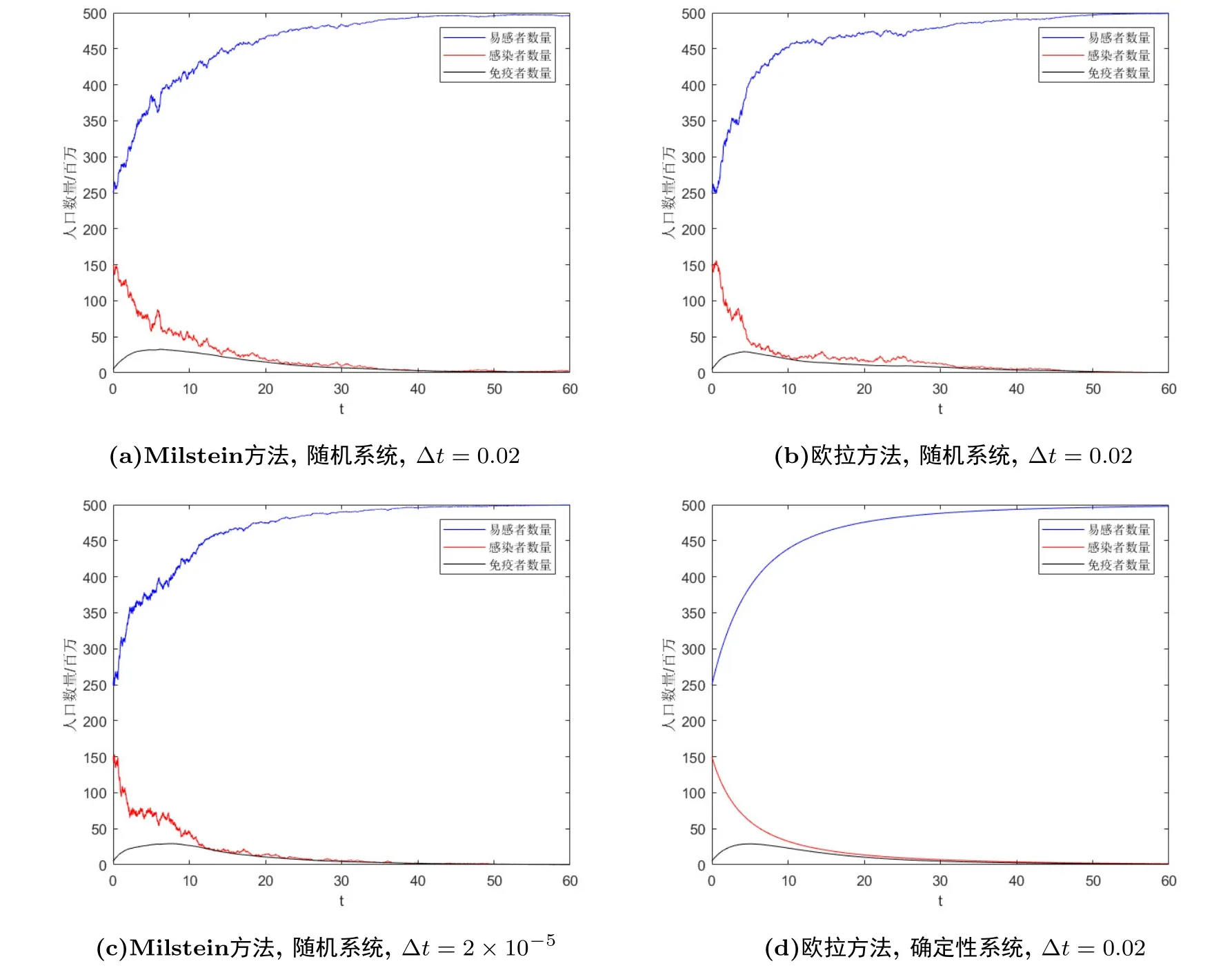
图1 σ =0.02,<1时的数值模拟图

相反的, 若提高传染率β = 0.1, 降低心理作用系数α = 0.05, 保持模型中的其他参数不变,则由计算可得

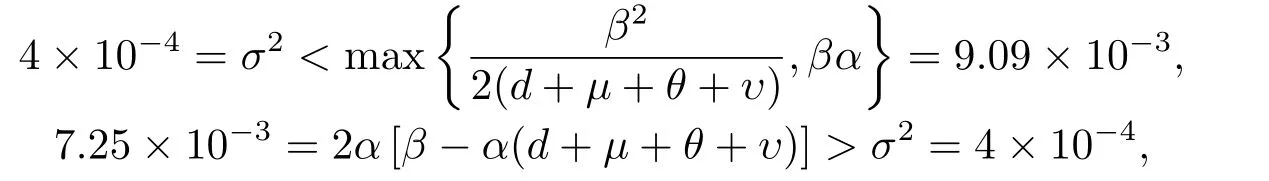
图2展示了此时的数值模拟结果, 表明此时疾病不再灭绝而是持久存在的.

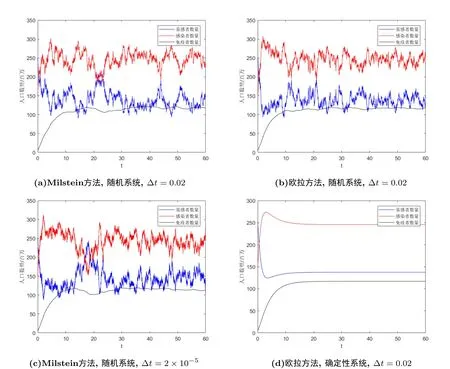
图2 σ =0.02,>1时的数值模拟图

更进一步, 若保持模型中参数不变, 仅将σ增大至0.1, 经计算可得

在某些情况下, 随机性模型中数值模拟的结果显示疾病将会灭亡, 但在其对应的确定性模型中数值模拟的结果显示疾病将会持续.因此随机扰动会对模型产生极大的影响.相比于确定性系统(2.2), 随机系统(1.5)中疾病灭绝的条件会相对弱.因此当系统(1.5)中的参数可以使疾病灭绝时, 同样的参数并不一定能保证系统(2.2)中的疾病灭绝.数值模拟图3(d)刻画了这一现象.

图3 σ =0.1,<1时的数值模拟图

值得注意的是步长∆t的取值会对系统解的路径产生影响.当步长∆t = 2 × 10−5时,S(t),I(t),R(t)的波动要比步长∆t = 0.02时更加显著.这说明越小的步长越能反应出在一个细微的时间段内系统解的变化情况, 而较大的步长可能会掩盖了在该时间段内系统解的某些显著变化.因此在计算机算力允许的条件下, 我们应该尽可能地选择较小的步长∆t.这在处理白噪声强度σ值较大的随机微分系统时更加的重要, 因为较大的σ值会使系统的扰动更加的剧烈.最后通过比较不难发现欧拉方法与Milstein方法在处理这类随机微分方程的效果上并没有显著的差异, 也没有出现系统解不收敛的情况.而在确定性系统中, 由于白噪声强度σ = 0, 因此Milstein方法退化成为欧拉方法, 故在这类系统中这两种方法的递推式是一样的.

3.基于心理作用的时滞随机SIRS传染病模型

由于大部分传染性疾病具有潜伏期, 因此当易感者被传染而转换成感染者之后并不会马上具有传染性.故在t时刻受到感染的易感者并不是被t时刻的感染者感染的, 而实际上是被t −τ时刻的感染者所感染的, 只是t −τ时刻的感染者在(t −τ)时刻没有表达出传染性.这体现了疾病传染的滞后性.在具有时滞的系统中, 时滞可能会影响到系统的稳定性, 引发系统的周期震荡, 因此时滞随机微分方程的动力学行为会更加复杂.考虑系统(1.5)具有时滞的情况,建立模型如下

且S(t)=N(t)−I(t)−R(t), 因此可以考虑上述方程组的等价模型

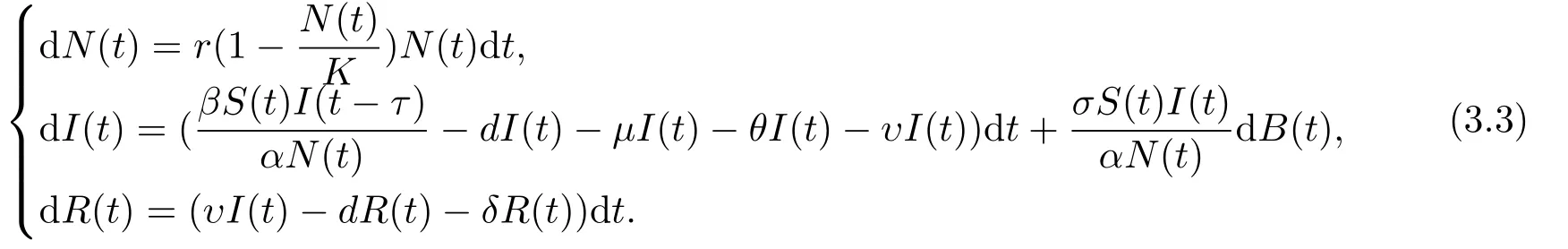
本节将证明系统(3.3)具有唯一的全局正解, 并绘制S(t),I(t),R(t)在不同时滞τ下对应的路径图.

Ⅰ 正解的存在性和唯一性

可以计算

其中A是独立于N,I,R,t的正常数.因此

对上式两端从0到τk∧T积分, 并取期望可得

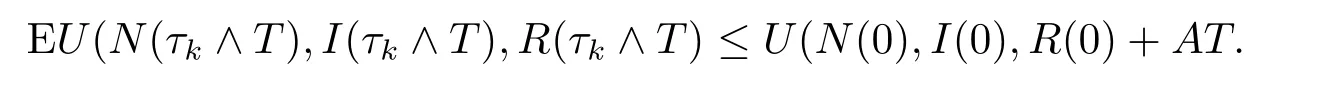
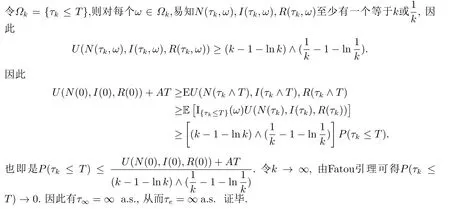
Ⅱ 数值模拟

在这一部分我们将使用高阶Milstein方法对系统的解进行模拟分析.

取初始时刻易感者人数250万人, 感染者人数150万人, 免疫者人数5万人, 即S(0) =250,I(0) = 150,R(0) = 5; 取传染率β = 0.05, 自然出生率b = 0.5, 环境容纳量K = 500,心理作用系数α = 0.1, 自然死亡率d = 0.2, 自然恢复率µ = 0.05, 治愈率θ = 0.2, 丧失免疫率δ =0.01, 获得暂时免疫率υ =0.1, 随机扰动σ =0.03, 分别取不同的τ值.则系统(3.1)的模拟结果如图4所示.

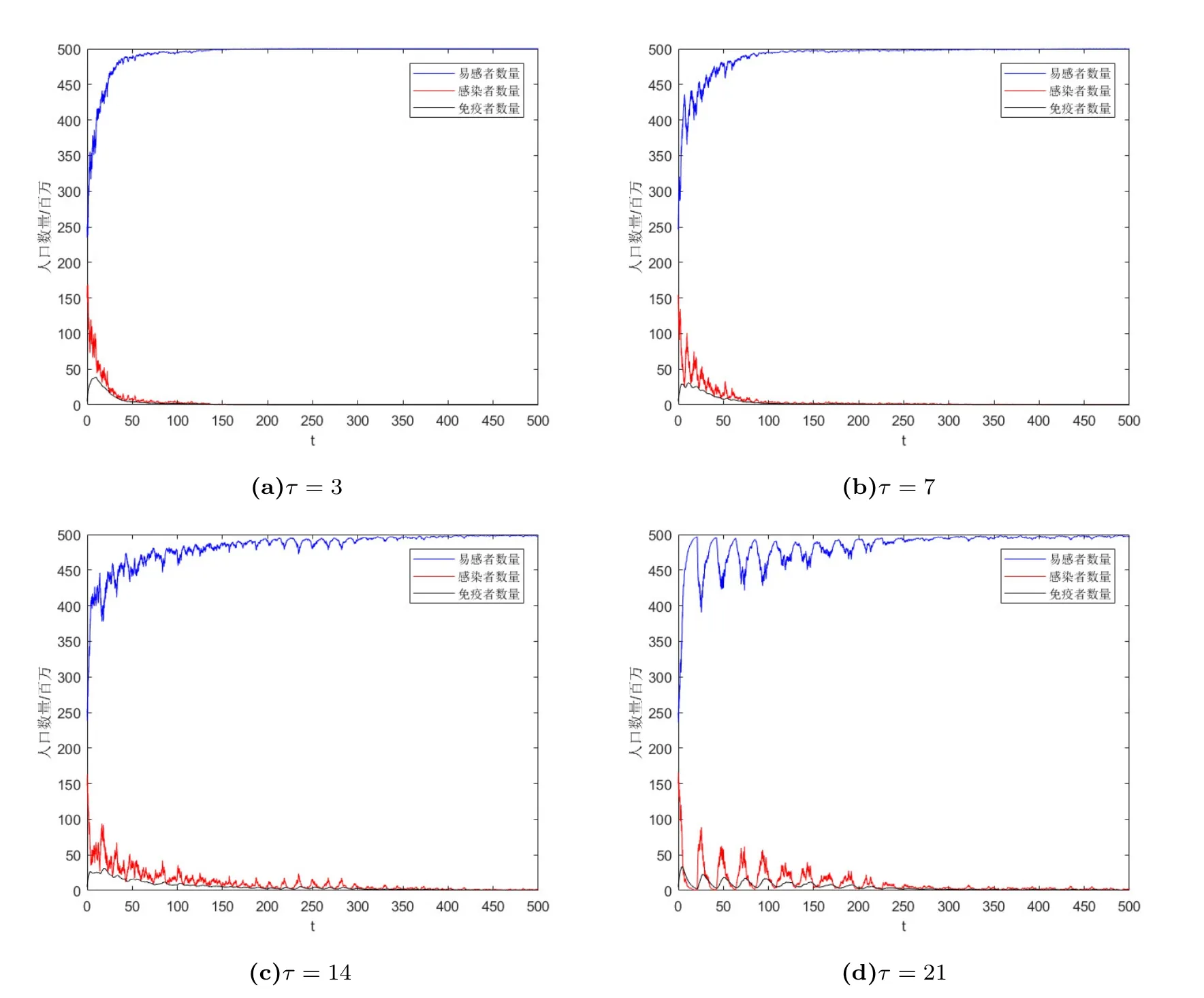
图4 T =500,∆t=0.02时的数值模拟图

可以看到疾病最终都将灭绝.但疾病灭绝所需要的时间随着时滞τ的增大而增大, 这说明当传染病的潜伏期较长时, 疾病往往需要更长的时间才能够灭绝.因此具有潜伏期的疾病将会更加的狡猾, 需要政府采取更长时间的隔离措施才能够有效地预防疾病的传播.COVID-19就具有较长的潜伏期, 我国政府也是根据该传染病的这种特性制定了入境人员14+7+7天的隔离措施, 收到了较好的成效.图4的(c)和(d)反映出感染者和易感者人数的变化具有波动性, 且振荡频率随着时滞τ的增大而增大.这说明当疾病的潜伏期较长时, 疾病的变化趋势是具有波动性的, 即疫情会出现反复, 这提醒决策部门在分析疫情时不能盲目乐观, 要考虑到这样的波动特性, 做好打持久战的准备, 时刻紧绷, 防患未然.COVID-19在我国的传染趋势就具有这样的波动性.复旦大学附属华山医院感染科主任张文宏也曾在2020年接受采访的时候表示要做好应对疫情反复, 甚至是第二波疫情的准备.

4.结论

本文研究了一类具有心理作用的随机SIRS传染病模型的动力学性质, 即模型解的存在唯一性, 灭绝性以及持久性.证明了当系统的白噪声强度较大或阈值≤1且白噪声强度不大时, 疾病将会灭绝; 当阈值> 1时, 对应系统的解将会持续.本文还研究了时滞对模型的影响.同时, 我们应用欧拉方法和Milstein高阶法模拟了不同参数下S(t),I(t),R(t)的路径图, 证实了本文建立的结论.