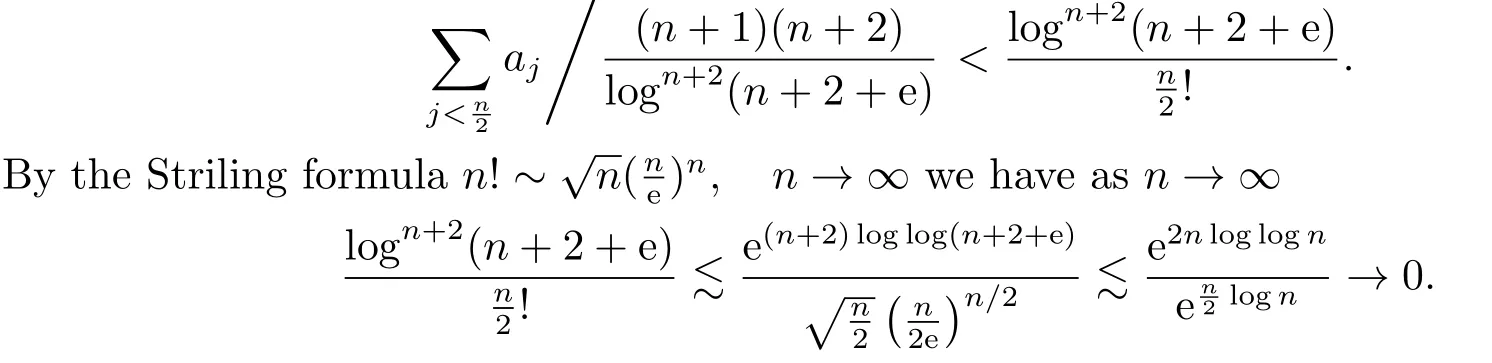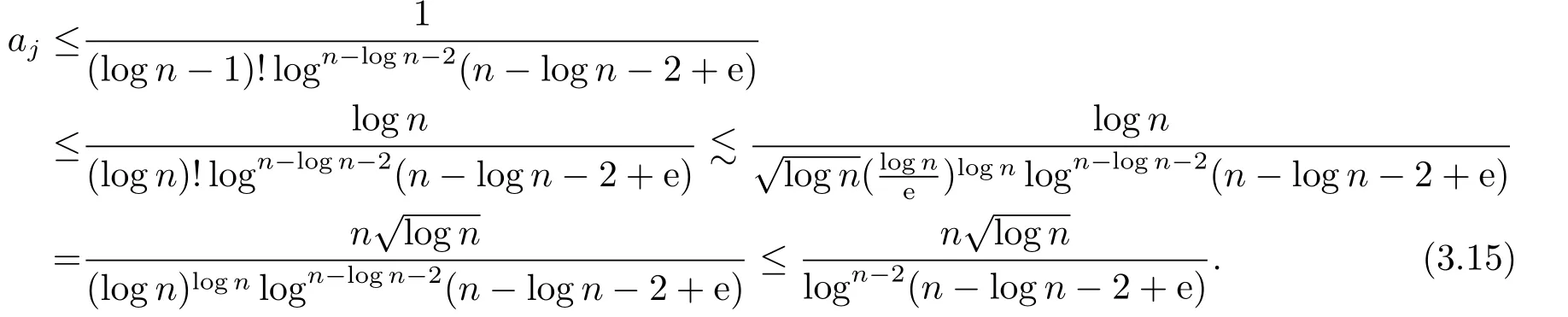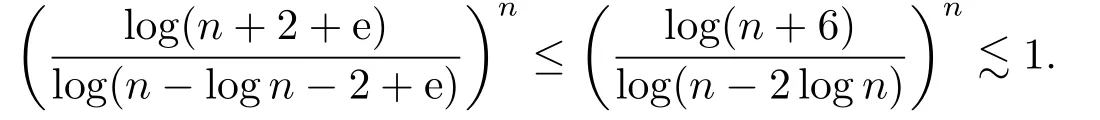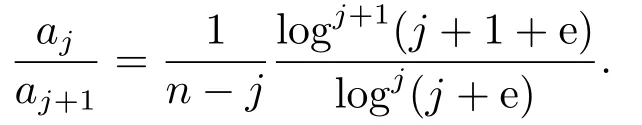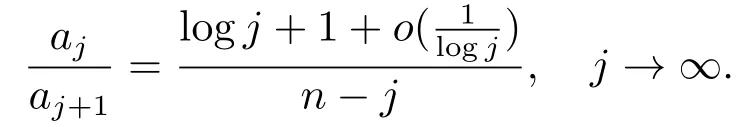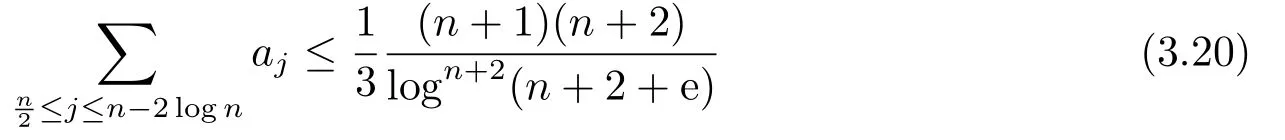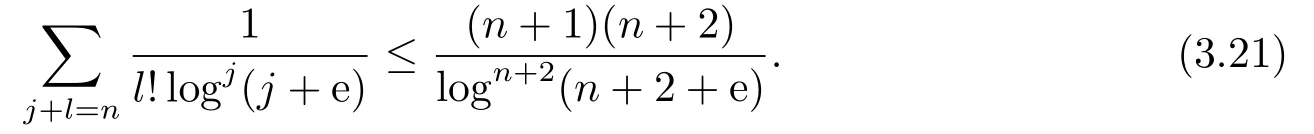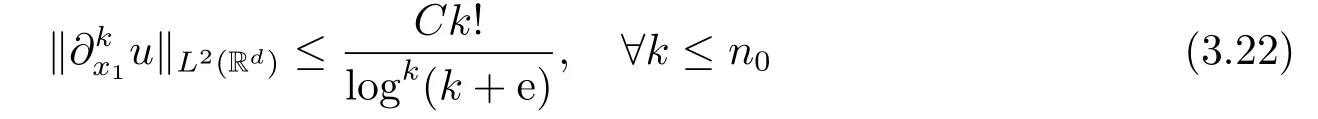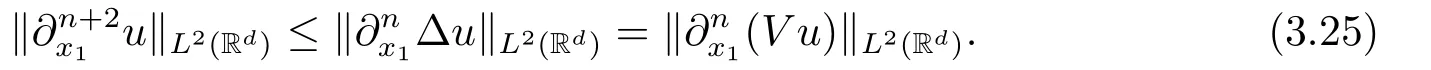Higher Derivative Estimates for a Linear Elliptic Equation

WANG Ming (王明)

(School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China)

Abstract: It is well known that the solution of the elliptic equation ∆u=V u is analytic if the potential V is analytic.But little is known on the ultra analyticity of the solution if V is ultra analytic.In this note, we show that the solution enjoys a log type ultra analyticity bound by an elegant and delicate induction argument.

Key words: Elliptic equation; Analyticity; Higher derivative

1.Introduction

Let u : Ω ⊂Rd→R be a smooth function.We say that u is analytic in Ω if for every x ∈Ω there exists C,R > 0 so thatholds for all multi-index α =(α1,α2,··· ,αd) ∈Nd, where we adopt the convention |α| = α1+α2+···+αdand α! =α1!α2!···αd!.The quantity R is often referred to the analytic radius at x.The analyticity of solutions for elliptic equation is a classical topic studied in references.If u(x) is harmonic inΩ, namely ∆u=0 in Ω, then u is analytic in Ω.[3]

Moreover, let L be an elliptic differential operator with analytic coefficients and O be an open disk in Rd.Then any solution of Lu=0 in O is analytic.For the details of this result,we refer the readers to [2, 6, 8, 9].In particular, consider the linear elliptic equation

If V is analytic on Rd, then the solution u of (1.1) is analytic on Rd.

We ask the following question.

Question:If V is ultra analytic, namely the analytic radius R = ∞, what can we say about the quantitative analytic bound for the solution of (1.1)?

To our best knowledge, the problem has not been solved in the references.The question is motivated by the quantitative analytic bounds of solutions and its applications in the observability inequalities for heat equations[1,4,10]and KdV equations[5,7].

To make the question more precise, we assume that there exists C0>0 so that

Our main result reads as follows.

Theorem 1.1Assume that (1.2) holds.Let u ∈L2(Rd) be a solution of (1.1).Then there exists a constant C >0 so that

In our recent paper [10], we have established a similar bound as (1.3) for fractional heat equation on Rd.The main strategy in [10] is to derive some quantitative estimates in Gevrey spaces Gσ, endowed with the norm

At this moment, we do not know whether the bound (1.3) is optimal or not.We hope to improve (1.3) to ∥u∥L∞(Rd)≤C|α|(α!)δ,∀α ∈Ndfor some δ ∈(0,1).But this is also open.

The notation in this paper is standard.We use AB to denote A ≤CB for some constant C >0.If both AB and BA hold, we write A ∼B.

2.Reduction Theorem 1.1 to Theorem 2.1

In this section, we show that Theorem 1.1 follows from some higher derivative estimates in one variable, which may be easier to deal with.

Theorem 2.1Let u ∈L2(Rd) be a solution of (1.1) with V satisfying

Then there exists a constant C >0 so that

Proof of Theorem 1.1 under Theorem 2.1Let u ∈L2(Rd) be a solution of

with V satisfying

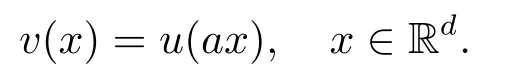
Then, by (2.3)-(2.4), v ∈L2(Rd) is a solution of

with W =a2V(ax) satisfying

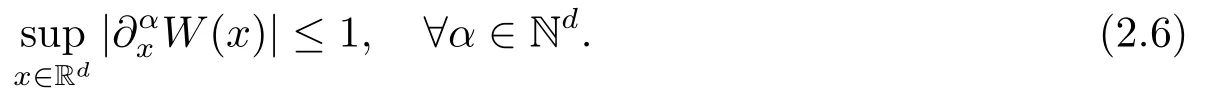
Suppose that Theorem 2.1 holds, then we apply Theorem 2.1 to v and conclude that for j =1,2,··· ,d

On the other hand, we have the inequality

which follows from the Plancherel theorem and the elementary inequality

Combining (2.7) and (2.8) we find

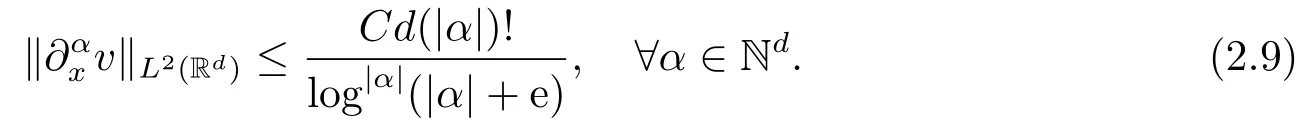
Note that u(x)=v(a−1x), we deduce from (2.9) that

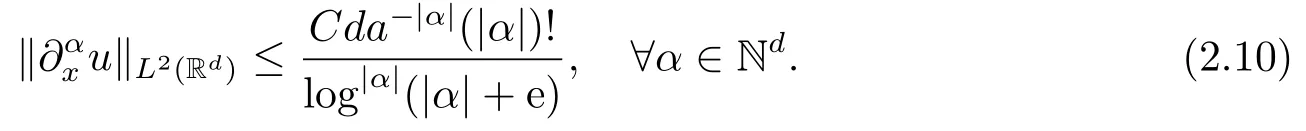
By the Sobolev embedding Hd(Rd)→L∞(Rd), we deduce from (2.10) that

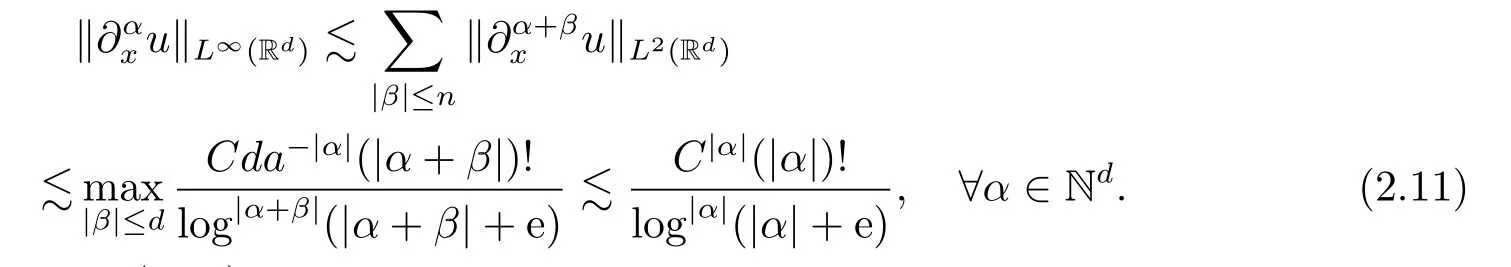
Combining the bound (2.11) and Lemma 2.2, we complete the proof of Theorem 1.1.

In the proof above, we have used the following lemma, which is of independent interest.

Lemma 2.2For all α ∈Nd, we have α!≥d−|α||α|!.

ProofLet α=(α1,α2,··· ,αd).It suffices to show that

where |α| = α1+α2+···+αd.We prove (2.12) by induction on |α|.Clearly, (2.12) holds for |α| = 0.Suppose (2.12) holds for all α satisfying |α| = k.Now we consider the case|α|=α1+α2+···+αd=k+1.Then in this case we have

This, together with the induction hypothesis, gives that

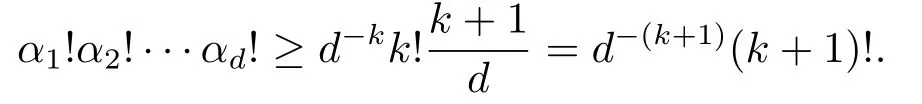
This shows that (2.12) holds for all α satisfying |α|=k+1.The proof is complete.

3.Proof of Theorem 2.1

Let

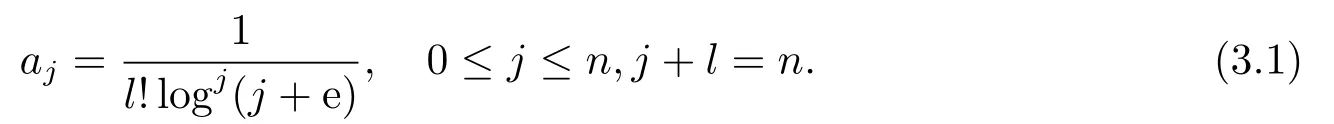
We first study the monotonicity of aj.

Lemma 3.1Let ajbe given by (3.1).Then when n →∞we have

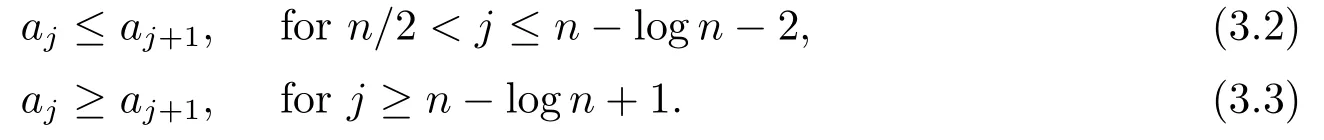
ProofThanks to the formula (3.1), we find that aj≤aj+1is equivalent to

Rewrite

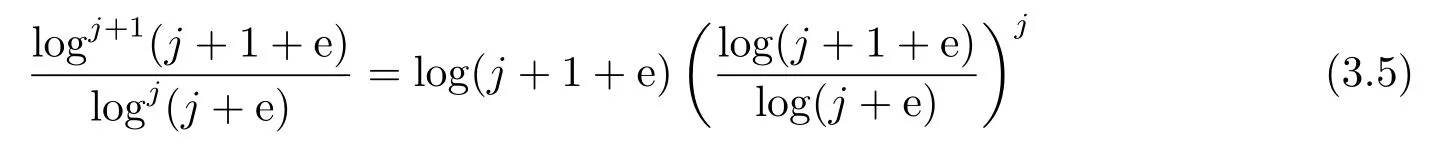
and

Note that

here and below we use o(1/jk) to denote a quantity less than or equal some constant times 1/jkas j →∞.Similarly,

Then we deduce from (3.6) that

Similarly,

Thanks to (3.7), we have

This, together with (3.8), gives that

Combining (3.4)-(3.5) and (3.9), we find aj≤aj+1is equivalent to

Thus in order to prove(3.2),it suffices to show that if n/2

Similarly, to prove (3.3), it suffices to show that if j ≥n −log n+1 then

In fact, if j ≥n −log n+1, then j +log j ≥n −log n+1+log(n −log n+1) ≥n holds if 1 ≥log n −log(n −log n+1).But this holds clearly if n is large enough.Thus (3.11) holds and the proof is complete.

The main estimate in this section is the following proposition, which is the key step in the proof of Theorem 2.1.

Proposition 3.2When n →∞we have

ProofLet ajbe given by (3.1).We split the sum as

Then we find

Thus for large enough n

2) The case j > n −2 log n.In this case, we have j > n/2 if n is large enough.So according to Lemma 3.1, we find

Recall the definition (3.1), we infer that if n −log n −2 ≤j ≤n −log n+1,

It follows from (3.14)-(3.15) that

This implies that

holds if one can show that

But this is equivalent to

Thus we deduce that

It follows that

So (3.17) holds if n is large enough.

3) The case n/2 ≤j ≤n −2 log n.By the definition of aj, we have

This, together with (3.5) and (3.9), gives

Moreover, according to (3.14) and (3.15), we have

Thanks to (3.18)-(3.19), similar to Step 2), we conclude that

for n large enough.In fact, in 2) we have shown a stronger result: log n∗RHS of (3.19) is less than or equal to RHS of (3.20).

Finally, combining (3.13), (3.16) and (3.20), we complete the proof.

Proof of Theorem 2.1Thanks to Proposition 3.2, there exists an integer n0> 0 so that for all n ≥n0

On the other hand,let u ∈L2(Rd)be a solution of ∆u=V(x)u.Then by the standard elliptic regularity and the smooth assumptions on V we find that, for every integer k, there exists a constant C(k)>0,∥u∥Hk+2(Rd)≤C(k)∥u∥Hk(Rd).Thus a bootstrapping argument shows that for every k ∈N, ∥u∥Hk(Rd)≤C(k).In particular, this implies that

for some constant C >0, where n0is the same to that fulfilling (3.21).

Now we claim that if

holds for some n ≥n0, then

In fact, by the Plancherel theorem and the equation ∆u=V(x)u, we have

Using the Leibniz rule, the assumption (2.1) and (3.23), we infer that

Here in the last step we used (3.21).Combining (3.25)-(3.26) gives the claim.

Finally, thanks to the bound (3.22) and the claim, we find that Theorem 2.1 holds.