气象因素影响下蚜虫的状态反馈生物防治模型分析

黄明湛, 刘守宗, 张莹

( 信阳师范学院数学与统计学院, 河南信阳 464000)

1.引言

蚜虫俗称腻虫或蜜虫, 主要分布在亚热带和温带地区, 是一种影响广泛的农业害虫.蚜虫科目繁多, 但所有的蚜虫均为植食性昆虫, 不同种类的蚜虫大都是喜欢以某一种植物为食, 比如麦长管蚜就主要以小麦为食.为了提高农作物产量, 人们采取多种手段治理害虫, 最常见的治理措施就是喷洒农药, 然而以化学杀虫剂为主的传统防治技术已经造成了诸多负面影响: 一方面由于害虫的抗药性, 使得农药被加倍使用, 从而农作物上的化学残留逐步加大, 不断危害人们的健康; 另一方面, 农药的大量使用会造成大气、土地、水等的严重污染, 继而引发各类环境问题[1].因此, 近些年来, 生物防治越来越多地被应用于蚜虫害控制.

蚜虫的生物防治, 就是利用蚜虫的天敌来控制或减轻蚜虫害.蚜虫在自然界的天敌很多,有昆虫、真菌、细菌、病毒和鸟类等[2−3].利用天敌的方法多种多样, 可归纳为保护利用、引进和生产释放三个方面.保护利用就是在各项农事活动中, 尽可能地避免杀伤天敌并积极创造有利于天敌繁衍的条件.引进就是从外地引进天敌来防控.生产释放就是通过人工繁殖大量天敌, 在适当的时机释放到田间, 增加天敌数量,进而控制蚜虫害[4].在引进或生产足够的蚜虫天敌之后, 如何合理将其释放到田间以获取对蚜虫较好的控制效果, 是大量学者研究的重要课题.

影响蚜虫种群数量改变的因素有很多, 例如农药的使用、环境容纳量、天敌的数量、气象因子和蚜虫自身的特性等[5].许多学者通过构建数学模型研究蚜虫种群的动态变化规律及其控制.例如文[6]中, 作者研究利用七星瓢虫控制蚜虫, 构建了具有阶段结构的捕食者-食饵模型, 考虑了两种群所有阶段的相互作用关系, 其数值分析的结果显示初始状态下的天敌害虫比率是生物控制的关键因素.文[7]利用时滞微分方程研究了具有七星瓢虫阶段结构的蚜虫-七星瓢虫系统模型.文[5]则建立了具有食蚜蝇阶段结构的蚜虫-食蚜蝇模型.然而在数学模型中引进气象因素影响的研究还相对少见.此外, 种群控制中引进状态反馈的思想近些年来受到大量研究者的关注[8−10], 但是关于蚜虫状态反馈生物控制的数学模型研究还很少.

本文将基于上述考虑, 构建一类带有气象因素影响的蚜虫生物防治模型, 并研究状态反馈控制下蚜虫种群的动态演化规律.

2.建立模型

文[5]考虑了一类气象因素影响下小麦蚜虫种群动态突变模型, 利用了广义Logistic增长形式, 并考虑了温度和湿度的影响.在此基础上, 我们构建如下常微分方程的蚜虫种群动态模型:

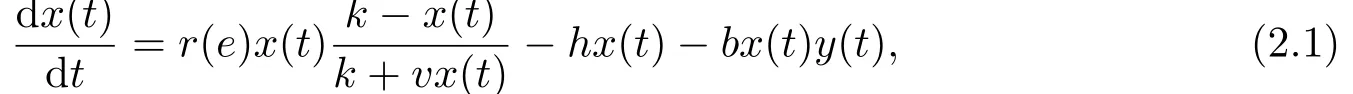
其中x(t), y(t)分别是t时刻蚜虫及其天敌的种群密度, r(e)表示蚜虫在天气因子影响下的内禀增长率, h > 0表示相对湿度.为广义Logistic生长, 其中k > 0为最大环境容纳量,v > −1.当v = 0时, 即为经典的Lgoistic生长.bx(t)y(t)表示天敌对蚜虫的捕食, 其中b > 0为捕食率.

函数r(e)解释了内禀增长率r和天气因子e之间的关系.内禀增长率主要受温度影响, 因此常将温度视为关键天气因素, 而不是考虑更多的天气变量.文[11-12]中, 定义了一种温度和内禀增长率之间的关系, 利用二次多项式函数拟合相应数据.基于非线性最小二乘估计方法, 导出了(2.2)中函数r(e)的表达形式, 具体变化曲线见图1所示.

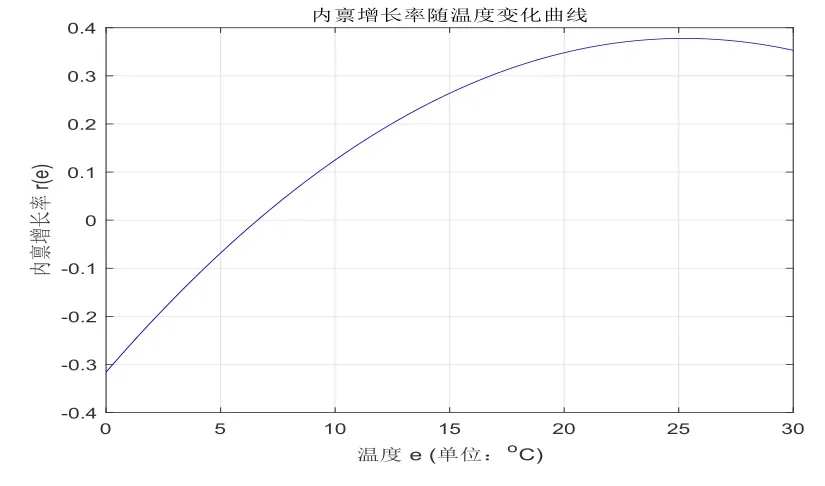
图1 内禀增长率r(e)随温度e的变化曲线.

考虑到蚜虫天敌的捕食效应, 我们建立如下蚜虫-天敌相互作用的捕食者-食饵系统:

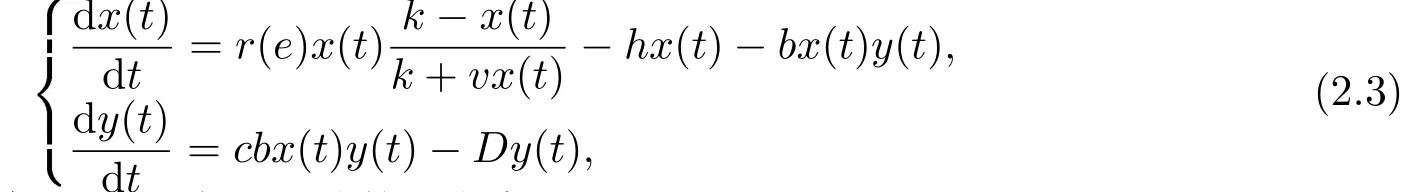
其中c>0表示转化率, D >0表示天敌的死亡率.

对于蚜虫的生物控制, 本文主要研究状态反馈脉冲控制, 即除去田间自然存在的天敌之外,当监测到田间蚜虫种群密度即将超过某经济阈值ET时, 向田间人为释放定量为τ的天敌.基于这样的操作形式, 我们可以建立状态反馈脉冲控制下的蚜虫生物治理模型如下:

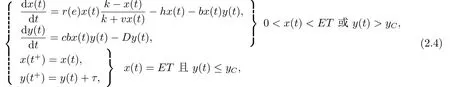
本文将借助于模型(2.4), 从理论和数值两个方面对蚜虫种群变化的动力学行为进行分析,并探讨温度、湿度以及天敌释放量对蚜虫种群发展的影响.

令M = {(x,y)|x= ET,0 < y ≤yC}, 则称M为状态反馈脉冲控制系统(2.4)的脉冲集.脉冲映射为φ(M)=N :(x,y)∈M →(x,y+τ)∈N.N称为系统(2.4)的相集.脉冲集中的点称为系统的脉冲点, 脉冲点经脉冲映射对应的点为其相点.

定义2.2[13]记Γ = f(P1,t)为阶1周期解, Γ称为是轨道渐近稳定的, 如果对于任意ε > 0,在相集上存在点P1的δ邻域U(P1,δ)(δ >0), 对于任意一点P2∈U(P1,δ), 以P2为初始点的半连续动力系统的轨线f(P2,t), 存在T, 当t>T时有ρ(f(p1,t),Γ)<ε.

定义2.3我们在系统(2.4)的相集N上定义坐标, 令相集N与x轴的交点坐标为0, N上任意一点B的坐标定义为B与x轴的距离, 记为yB, 设由点B出发的轨线与脉冲集M交于一点D,点D的脉冲相点为点B1∈N上, 坐标为yB1.我们定义点B的阶1后继点为B1, 点B的阶1后继函数为F1(B)=yB1−yB.

注2.1若F1(A)=0, 则从点A出发的轨线Γ就是系统(2.4)的阶1周期解.

引理2.1[13]后继函数F1(A)是连续的.

3.动力学行为分析

I 无控制系统(2.3)的动力学性质

通过平衡点的稳定性分析, 可得如下结论：

定理3.11) 当r(e) < h时,系统(2.3)的平衡点O(0,0)是稳定的结点; 当r(e) > h时, 平衡点O(0,0)是不稳定的鞍点;

证1) 计算系统(2.3)在O点的Jacobian矩阵, 得到

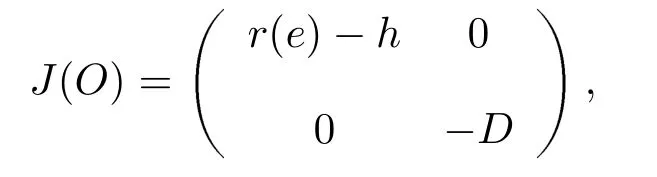
它的特征多项式为(λ+D)[λ −(r(e)−h)] = 0, 其中两个特征根为λ1= −D,λ2= (r(e)−h).所以当r(e)h时, O(0,0)为鞍点.

2) 计算系统(2.3)在E1点的Jacobian矩阵, 得到

它的特征多项式为(λ −λ1)[λ −λ2]=0, 两特征根分别为

3) 计算系统(2.3)在E2点的Jacobian矩阵, 得到

II 控制系统(2.4)的动力学性质

下面我们将应用微分方程几何理论和后继函数的方法, 讨论蚜虫生物控制系统(2.4)的周期解的存在性, 唯一性以及系统的吸引域.

这说明后继函数F1(P)在直线段上是单调递减的, 再根据阶1周期解存在性的证明可知,系统的相集上存在唯一的点M使得F(M) = 0, 即系统(2.4)存在唯一的阶1周期解(如图2(b)所示).证毕.

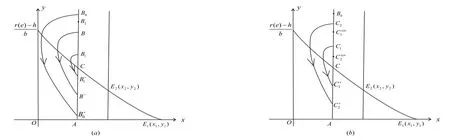
图2 (a)阶1周期解的存在性; (b)阶1周期解的唯一性

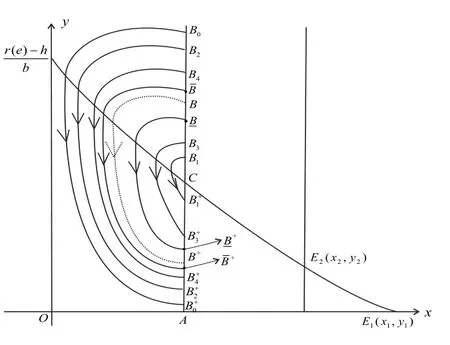
图3 系统(2.4)的吸引域的存在性

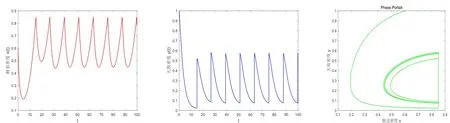
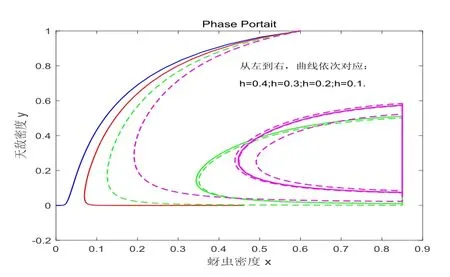
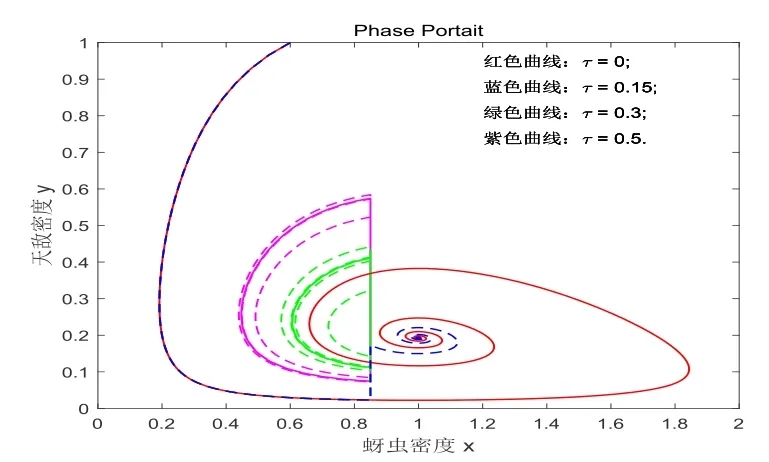
综上所述, ∆Ω是系统(2.4)在{(x,y)|0

注3.1若果点及重合为一点, 即=B =, 那么吸引域∆Ω即为定理3.1及定理3.2中的阶1环, 这种情况下, 定理中存在的阶1周期解就是轨道渐近稳定的.

4.数值模拟及生物控制影响因素分析

在这一节中, 我们将通过数值分析的方法验证上述理论的正确性, 并对生物控制效果的各影响因素进行探讨.

根据内禀增长率r和温度e之间的关系式(2.2), 当温度在0◦到30◦之间变化时, 内禀增长率r的取值大概落在区间[−0.3160,0.3778]内.文[14]的研究发现, 温度条件成为病虫害发生或流行的主要控制因子, 气温与病虫害的发生有显著的正相关关系, 其相关系数为0.703, 而降水与病虫害的相关性较差, 相关系数仅为0.094.我们首先选择内禀增长率r(e) = 0.35, 湿度参数为h=0.1.选取其余参数取值为k =5,v =0.5,b=0.8,c=0.5,D =0.4.

图4 系统(2.4)的阶1周期解

为观察温度对两类种群发展的影响, 我们保持其他参数不变, 选择五类不同的温度值, 分别是e = 8◦;e = 9.5◦;e = 10◦;e = 14.5◦;e = 20◦.依据内禀增长率和温度之间的关系, 依据图5我们可以看到,当温度较低时, 例如e = 8◦, 蚜虫的内禀增长率较低, 导致蚜虫数量很少, 最终出现蚜虫和天敌数量均趋向零.随着温度的升高, 当温度e=9.5◦;e=11◦时, 观察到在相同的释放条件下, 两类种群的数量最终趋向一个正平衡点.随着温度继续增加, 蚜虫的增长率进一步提高, 当温度e = 14.5◦;e = 20◦时, 系统中两类种群的数量呈现出稳定的周期变化.总的来说, 温度越高, 蚜虫种群的密度越大, 即相对较高的温度有利于蚜虫的生长, 对其生物防控的难度越大.

图5 温度变化对两类种群发展的影响

为了解湿度对蚜虫生物防治的影响, 我们固定温度取值在20◦, 并允许湿度参数在一个更大的范围变化.为此, 我们选择湿度参数h的四组不同取值, 分别是h = 0.1,h = 0.2,h =0.3,h = 0.4, 如图6所示.可以看到, 随着湿度的增加, 蚜虫及其天敌的数量变化也出现了三种状态, 即趋向灭绝、趋向一个边界平衡点以及形成周期震荡变化.可以观察到, 在此温度条件下, 较大的湿度对蚜虫发展具有一定抑制作用.

图6 湿度变化对两类种群发展的影响

为考查天敌释放量对蚜虫生物防治的影响, 我们仍固定温度取值在20◦, 湿度参数为h =0.1, 也选择了释放量τ的四个不同取值, 分别是τ =0,τ =0.15,τ =0.3,τ =0.5, 如图7所示.我们观察到, 当τ =0时, 即不采取人为生物防治措施, 蚜虫和天敌的种群数量将趋于一个正平衡点.当τ =0.15时, 即释放量较小时, 蚜虫的种群数量在经历了若干次脉冲作用后, 还是趋于正平衡点.随着释放量继续增加, 当τ = 0.3,τ = 0.5时, 蚜虫和天敌的种群数量最终形成稳定的周期震荡.与我们的预期相一致,图7显示天敌的释放量越大, 蚜虫种群发展受到的抑制作用越强.

图7 天敌释放量对两类种群发展的影响

5.小结

本文针对蚜虫的生物防治, 构建了一类带有气象因素影响及状态反馈脉冲控制机制的半连续动力系统, 分别讨论了无控制系统以及控制系统的动力学行为, 并利用数值分析的方法,研究了温度, 湿度以及天敌释放量对蚜虫和天敌种群发展的影响.研究结果显示, 通过状态反馈和生物防治, 可以有效地将蚜虫种群密度控制在预期水平之下.此外,温度、湿度等气象因素对蚜虫种群的发展以及其生物控制的结果有显著影响, 而天敌的释放量越大, 对蚜虫的整体控制效果越好.