次线性期望空间下END阵列加权和的完全收敛性
2022-07-07陈晓聪吴群英
陈晓聪, 吴群英
(桂林理工大学理学院, 广西桂林 541004)
1.引言及引理
极限理论是数理统计的重要研究课题, 它在数学、统计和经济等领域得到广泛运用.随着极限理论在金融、风险度量等领域的应用不断深入, 只在模型确定的条件下成立的经典极限理论局限性逐渐突显, 为此, 彭实戈[1]院士率先提出了次线性期望空间理论, 并建立了次线性期望空间的完整理论体系.次线性期望为解决次线性概率问题提供了一个更为灵活的框架, 近年来引起了广大学者的关注和研究, 并取得了许多相关的研究成果.ZHANG[2−4]研究了次线性期望下的END随机变量序列的Kolmogorov强大数定律, 推广得到了次线性期望空间下的指数不等式和Rosenthal’s不等式, WU和JIANG[5]在次线性期望下对强大数律和Chover’s重对数律进行了研究和推广, 马晓晨和吴群英[6]得到了END序列加权和的完全收敛性.
1947年, 完全收敛性首次由统计学家HSU和ROBBINS提出, 目前, 在概率空间中关于完全收敛性的研究已经取得了许多成果.如BAO等[7]研究了行END阵列加权和的收敛性.由于次线性期望和容度不具有线性性, 一些适用于传统概率空间的方法不再适用于次线性期望空间.本文在现有的理论基础上, 将文[7]中的定理2.1END阵列加权和的完全收敛性, 从概率空间推广到次线性期望空间, 得到比文[6]更强的结果.
我们使用彭实戈院士[1]所构建的次线性期望空间的基本概念和框架, 假设(Ω,F)是给定的可测度空间, H是定义在(Ω,F)上由实函数所构成的线性空间, 如果X1,··· ,Xn∈H, 则对∀φ ∈Cl,Lip(Rn), 有φ(X1,··· ,Xn) ∈H, 其中Cl,Lip(Rn)表示在线性空间的局部Lipschitz函数, 即对任意Cl,Lip(Rn), 存在常数c > 0, m ∈N的选取取决于φ, 使得对任意x,y ∈Rn, 都有|φ(x)−φ(y)|≤c(1+|x|m+|y|m)|x −y|.也称H是由随机变量所构成的空间, 并记X ∈H.
定义1.1[3]次线性期望ˆE:H →[−∞,∞], ˆE 满足下列四个条件:
1) 单调性: 如果X ≥Y, 则ˆE(X)≥ˆE(Y);


2.主要结果及其证明

注定理2.1是将文[7]中定理2.1的相应结论从概率空间推广到了次线性期望空间, 将有限加权和延伸到了无限加权和, 得到了更一般的结果.相比较于文[6]的定理2.1中同分布条件, 本文的随机控制条件更弱, 同时将结论从END随机变量序列推广到END随机变量阵列, 得到的结果范围更广.


根据定义1.4以及(2.9)和(2.10)有

于是, 由(2.2)和(2.11)可得
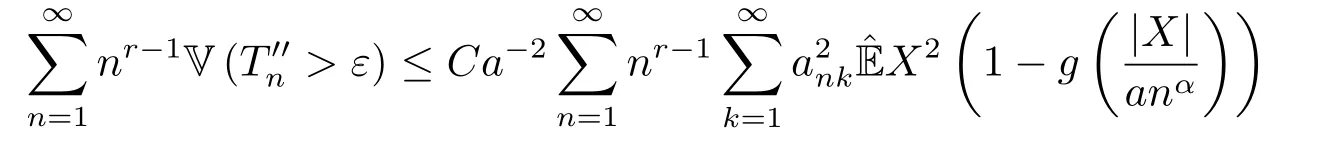


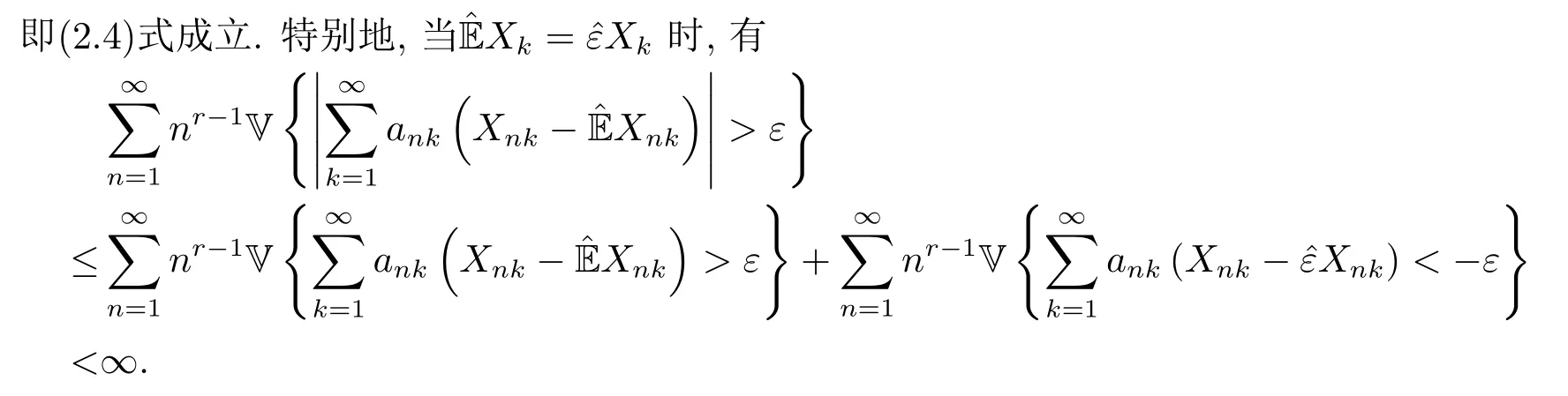
从而得到(2.5)式, 即完成了定理2.1的证明.
