带非线性阻尼和衰退记忆的抽象发展方程的时间依赖吸引子

胡阳阳, 任永华, 张建文

(太原理工大学数学学院, 山西晋中 030600)

1.引言

设Ω ⊂R3是带有光滑边界的有界区域, 考虑如下方程

其中, h(x)∈L2(Ω).ε=ε(t)是一个递减的有界函数, 满足

且存在常数M >0, 使

函数a(x)满足

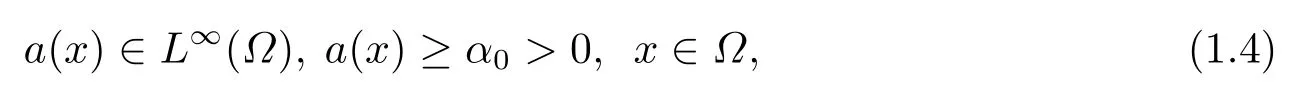
其中α0是一个正常数.非线性阻尼g ∈C1(R), 满足: g(0)=0, g是严格递增函数, 且

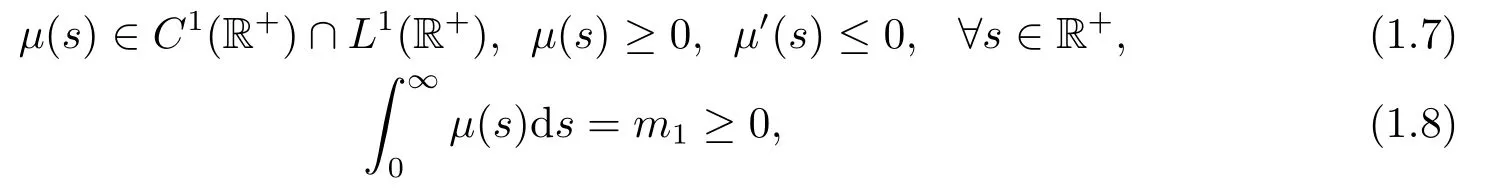
ρ是一个正常数.非线性项函数f ∈C1(R), f(0)=0,满足以下增长条件

和耗散性条件

其中λ1是算子A=−∆在空间Ω)中的第一特征值.

模型(1.1)是对一类粘弹性固体的描述, 其由于周围介质的粘性阻力而具有衰退记忆和耗散性特征.

对于问题(1.1), 当ε是一个与t无关的常数时, 首先, 汪璇, 任利宁在文[1]中讨论了有界域Ω ⊂R3上带衰退记忆的方程

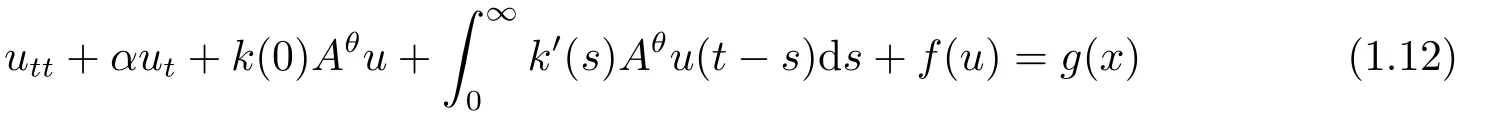
全局吸引子的存在性; 在文[1]的基础上, WANG等人[2]研究了有界域Ω ⊂Rn上该方程解的渐近行为.

当ε为关于t的函数时, 此时问题变得更加复杂.这是因为即使外力项与时间t无关, 方程仍然需要在非自治框架下考虑, 这意味着采用经典的半群理论已经不能准确描述系统的耗散机制.为了解决这一问题, 在文[3]中, Conti等人根据拉回吸引性中的最小性提出了时间依赖吸引子的概念, 并基于Plinio等人的理论[4], 构造了一个证明时间依赖吸引子存在的充分条件.进一步, 他们研究了时间依赖空间上吸引子的渐近结构[5].基于这些理论, 胡弟弟, 汪璇[6]讨论了记忆型无阻尼抽象发展方程时间依赖吸引子的存在性.

最近, MENG和ZHONG等人[7]研究了具有非线性阻尼g(ut)的波方程在时间依赖空间上解的长时间行为, 他们通过定义压缩函数证明过程的渐近紧.随后在文[8]中, MENG, LIU提出了时间依赖吸引子存在的充要条件.MA等人[9−10]研究了带非线性阻尼的记忆型波方程和Plate方程解的长时间行为.

目前, 还没有人对带非线性阻尼和衰退记忆的模型(1.1)进行讨论和研究.一方面, 研究问题的吸引子, 最关键的是获得过程的紧性.考虑到方程(1.1)中含有记忆项, 故文[8]中的方法有了局限性.另一方面, 临界非线性阻尼项的存在意味着算子分解方法不再适用.为此, 本文中先构造一个三元解空间, 在其上做先验估计, 然后利用压缩函数理论获得了过程的渐近紧, 由此证明了方程(1.1)时间依赖吸引子的存在性.

为了估计的方便, 文中出现的C和Ci均表示正常数, 在不同之处可表示不同的估计值.

2.预备知识和准备工作

引入变量η = ηt(x,s) = u(x,t)−u(x,t −s), 设µ(s) = −k′(s), k(∞) = 1, 方程(1.1)可以转化为

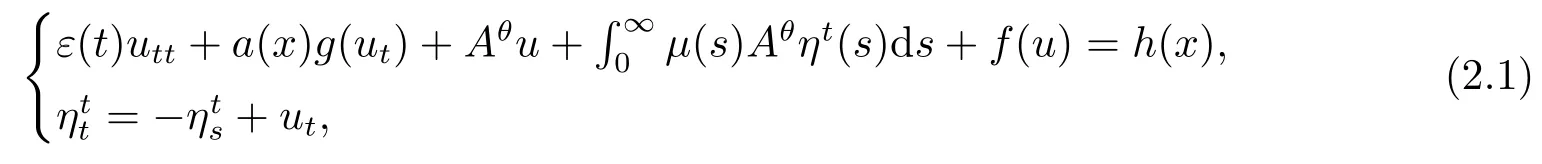
对应的初边值条件为

3.适定性和时间依赖吸收集

其中η是充分小的正常数, 具体范围见后文.

现在, 用ut+δu乘(2.1)式并在Ω上积分, 有

记Eδ(t)=E1(t)+δε(t)(ut,u), 后面其余部分记为W(t), 则有

4.先验估计

这一部分主要是为了获得估计(4.12)-(4.14), 用于证明过程的渐近紧.

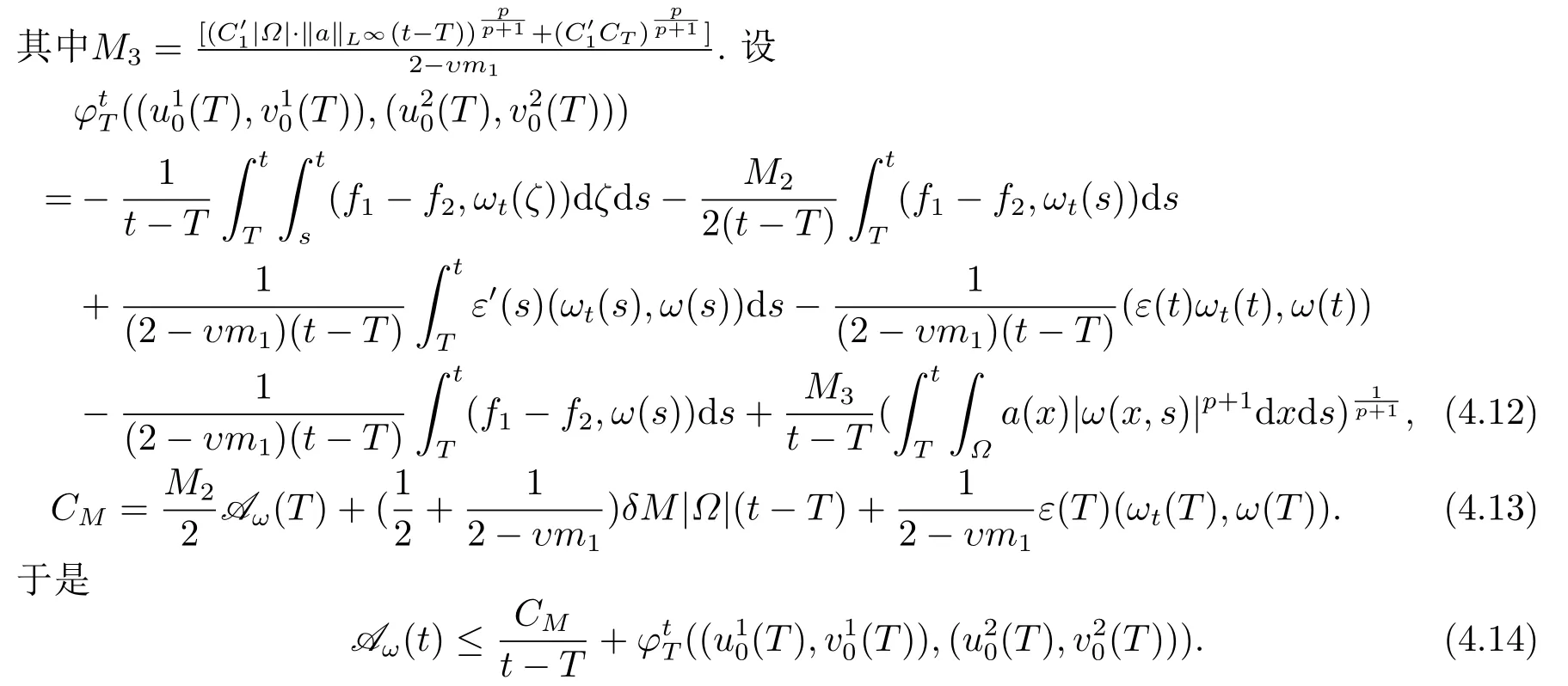
5.渐近紧

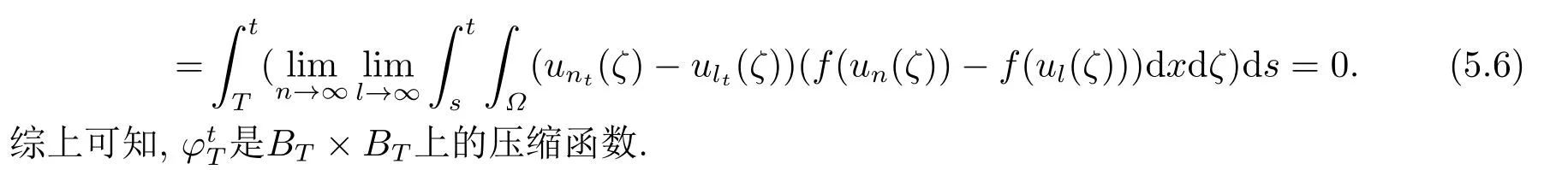
6.时间依赖全局吸引子的存在性

定理6.1假设条件(1.2)-(1.11)成立, 由方程(1.1)产生的过程U(t,τ):Hτ→Ht拥有不变的时间依赖全局吸引子U ={At}t∈R.

证根据引理2.2, 引理2.3, 引理3.1和定理5.1可得, 存在唯一的时间依赖全局吸引子U ={At}t∈R.进一步, 由引理3.2中过程的强连续性证明知, U 是不变的.