城市型水库溃坝生命损失估算研究

杨德玮，周克发，董 凯，张雄杰

（1.南京水利科学研究院，江苏 南京 210029； 2.水利部 大坝安全管理中心，江苏 南京 210029）

我国已建成各类水库大坝98822 座，总库容约为8953 亿m3［1］。 大坝溃决是典型的突发公共安全事件，如1975年强台风暴雨洪水导致板桥和石漫滩两座水库溃坝，直接导致22564 人死亡并造成严重的生态环境破坏［2-3］。 通常水库地理位置多处于远离城市的山区，水库下游洪水下泄范围内人口较少。 城市型水库［4］是指为满足城市的供水防洪需要建设的水库或者因城市逐渐发展和城区扩张而被纳入城市边缘的水库，如广东省深圳市龙口水库、河南省郑州市常庄水库等。 城市型水库主坝如果发生溃坝险情，则大量水体倾泻向人口等高度集中的城区，其产生的灾害严重性远大于一般水库［5-6］，因此溃坝生命损失估算对于城市型水库的运行和管理更为关键。

溃坝生命损失模型自20 世纪80年代提出，目前国外应用的生命损失计算方法主要有Brown ＆Graham 法、 Dekay ＆ McClelland 法、 RESCDAM 法等［7-8］，考虑的溃坝生命损失影响因素如下：风险人口、预警时间、洪水强度、风险人口死亡率、洪水严重程度影响系数和修正系数等［9］。 由于我国与发达国家在社会因素与经济环境方面存在很大差异，因此国外的研究成果并不完全适用于我国实际情况。 国内学者基于我国溃坝资料提出许多适用性更好的研究成果，如周克发等［10］基于8 座水库溃坝资料建立了我国水库溃坝的风险人口死亡率表，提出了符合我国实际溃坝情况的生命损失评价模型。 随着现代数学的发展和应用，诸多学者将新的数学模型应用到溃坝生命损失估算中，如模糊数学［11-12］、区间理论［13］等。

以往学者提出的估算模型中计算参数的选取大多针对偏远山区的水库大坝，对于城市型水库的适用性少有涉及。 笔者以DP-DFY 城市型水库为例开展溃坝生命损失估算研究，通过分析Dekay ＆ McClelland法和李-周法估算结果的合理性，分析已有估算方法对于城市型水库的适用性，以期为城市型水库溃坝生命损失估算参数取值提供支持。

1 工程概况

1.1 城市概况

甲市地貌以丘陵岗地为主，总面积超过1 万km2，下辖4 个区、4 个县、1 个县级市以及4 个经济开发区。截至2019年年底，全市常住人口818.9 万人，其中城镇人口占比76%。 城区区划与市区水系情况如图1 所示。 该市所处流域内洪水随暴雨呈现季节性规律，主要集中在夏季，其他月份出现洪水的概率低且峰值小。

图1 甲市城区区划及水系分布

1.2 水库工程概况

甲市共有两座城市型水库，Ⅰ、Ⅱ水库均位于B区，为城市提供防洪和供水功能，同时兼顾生态补水功能。

（1）Ⅰ水库。 水库枢纽由主坝、泄洪涵洞、溢洪道和连通输水隧洞等组成。 主坝为均质土坝，坝轴线近南北向，全长2876 m，坝顶高程36.00 m，最大坝高26.0 m。 大坝上游坡采用干砌块石护坡，高程33.10 m以下坡比1 ∶3，高程34.30 m 以上坡比1 ∶2；大坝下游坡采用草皮护坡，高程27.50 m 以上坡比1 ∶2，高程27.50 m 以下坡比1 ∶2.5。 总库容2.42 亿m3，防洪标准为1000 a 一遇，按可能最大洪水（PMF）校核，洪水过程线见图2。

图2 PMF 洪水过程线

（2）Ⅱ水库。 水库枢纽由主坝、泄洪涵洞、正常溢洪道、非正常溢洪道和连通输水隧洞等组成。 主坝为均质土坝，全长2134.8 m，坝顶高程34.00 m，最大坝高24.5 m。 上游坡采用混凝土正六边形预制块护坡，坡比1 ∶3；下游坡采用草皮护坡，坡比1 ∶2.5。 总库容1.77 亿m3，防洪标准为500 a 一遇，按可能最大洪水（PMF）校核。

2 溃坝洪水严重性和风险人口

2.1 溃坝洪水流量分析

根据工程设计与水库控制运用原则，结合防洪工程与流域内最大暴雨洪水量级，分析判断两座水库基本不会出现漫顶溃坝，但存在管涌破坏的可能。 主要考虑超标准洪水或不均匀沉降造成上下游压力差过大，导致渗透破坏，最终引发管涌溃坝。 因此，本研究假设最危险工况为：遭遇PMF 洪水，水库初始水位为汛限水位28.00 m，入库流量为PMF 洪水过程，水库按照防洪调度原则进行泄洪，当坝前水位到达最高水位时，Ⅰ、 Ⅱ水库主坝同时发生管涌溃坝。 采用BREACH 模型［14-15］计算溃口洪水，获得溃坝洪水流量。

2.1.1 计算参数的选取

根据水库大坝的工程资料，确定溃口计算所需的输入参数，见表1。 根据水库水位与库容、面积等资料绘制Ⅰ、Ⅱ水库水位—库容—面积关系，如图3 所示。

图3 水库水位—库容—面积关系

表1 水库溃口计算输入参数

2.1.2 计算结果

Ⅰ水库溃坝时库水位34.5 m，主坝于坝高7.65 m处发生管涌溃坝，最终溃口深26.0 m、宽50.7 m；Ⅱ水库溃坝时库水位33.64 m，主坝于坝高10.7 m 处发生管涌溃坝，最终溃口深24.5 m、宽38.3 m。 将两个水库溃口流量按时间对应叠加，绘制总体溃口流量过程线，见图4。 计算结果显示，溃口流量在0 ～3 h 内迅速增大，约在第4.25 h 达到峰值8251 m3／s，而后随溃口流量逐渐减小，总水量为49753.64 万m3。

图4 水库主坝同时溃坝流量过程线

2.2 溃坝洪水淹没范围

本研究采用二维水动力模型进行洪水演进模拟，采用非结构化网格对地形重构剖分，结合研究区域的河道数据与地形数据，构建网格模型，确定上下游边界。 设定上游边界条件为BREACH 模型计算得到的Ⅰ、Ⅱ水库溃坝溃口洪水过程线；下游边界条件为X湖多年平均最高水位。

通过求解二维浅水方程的数值近似解［16］，得到溃坝洪水演进过程，以及洪水的峰值流量、流速、水深和过水断面宽度。 图5 为溃坝洪水演进模拟过程，溃坝洪水自坝址沿河道向下游演进，淹没城市面积共127 km2。 图6 为溃坝洪水演进区域内最大流速分布，Ⅰ、Ⅱ水库坝址处最大流速分别为26、28 m／s，溃坝后演进速度极快。

图5 溃坝洪水演进模拟结果

图6 溃坝洪水最大流速分布

根据计算结果可知，城市型水库溃坝洪水抵达人口密集区时间较短。 洪水携带巨大动能，会对下游居民生命和财产造成重大损失。

2.3 溃坝洪水严重性计算

2.3.1 计算公式

溃坝洪水严重性（Sd）反映洪水风险范围内公众和社会财产受到洪水灾害的破坏程度。 溃坝洪水严重性可用溃坝洪水在计算区域内的水深D和对应点洪水的平均流速V的乘积来表示，但实际应用中往往采用某个计算断面水深与流速平均值的乘积DV值来表示Sd，计算公式如下：

式中：Qdf为溃坝所引起的某个计算断面的流量，m3／s；Q2.33为同断面下的年均流量，m3／s，一般取Q2.33=0；Wdf为同断面溃坝所引起的最大洪水泛滥宽度，m。

DV值判别溃坝洪水严重性关系对照见表2［17］。

表2 DV 值判别溃坝洪水严重性关系对照

2.3.2 代表性区域选取

本研究选取各乡镇、街道的代表性区域进行洪水严重性计算，以代表各乡镇、街道总体洪水严重性情况。 针对城市型水库的特点，提出选取原则：综合考虑各区域的淹没水深和到达时间，选取淹没区域的居民小区或者村庄，如果区域内无村庄、小区，则合理选择受灾影响较大的工厂或者农田作为代表性区域。 由此确定各代表性区域分布如图7 所示。

图7 各乡镇、街道代表性区域分布

2.3.3 计算结果

根据式（1）计算得到各代表性区域的洪水严重性数据见表3。 由表3可知，在研究区域内存在5 个高度严重受灾区域，分别为B1 镇、B4 街道、B10 街道、C1街道和B8 街道。 B1 镇与B4 街道是城市内遭受洪水灾害程度最为严重的区域，B1 镇DV值为168.34 m2／s、B4 街道DV值为88.18 m2／s，而其他高度严重区域的DV值均在8～12 m2／s 内。

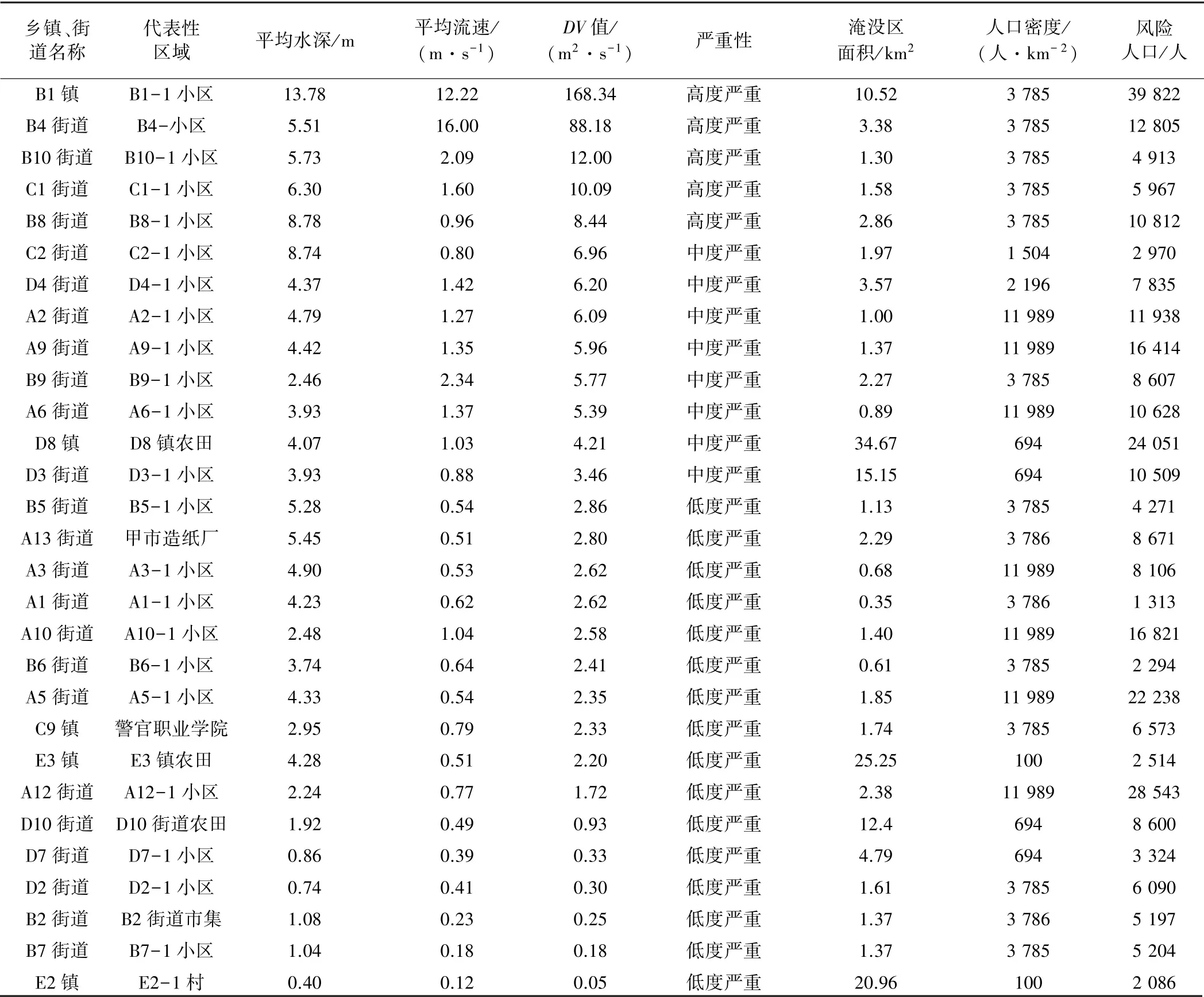
表3 洪水严重性及风险人口计算结果

2.4 城市风险人口计算

3 溃坝生命损失估算

生命损失LOL是指溃坝洪水向下游演进过程中造成的死亡人数，估算结果反映溃坝洪水灾害的严重程度。 本研究采用Dekay ＆ McClelland 法（以下简称D＆M 法）和李-周法进行溃坝洪水的生命损失估算。

3.1 D＆M 法

D＆M 法考虑警报时间对溃坝洪水造成生命损失的影响以及生命损失和风险人口之间的非线性关系，计算公式如下：

式中：F为溃坝洪水严重性Sd的函数符号，对于高度严重洪水F=1，低度严重洪水F=0，中度严重洪水F=0.5；WT为警报时间，代表洪水险情发生后政府向公众发出警报到最终洪水流经区域的时间，h。

为便于计算，式（2）通常简化为

3.2 李-周法

李-周法［19］是更符合我国实际溃坝情况的生命损失评价方法，计算公式如下：

式中：f为风险人口死亡率，按照特定的风险人口死亡率（见表4），结合具体情况选取；a为对下游造成灾难严重性程度系数，即风险人口死亡率修正系数。

表4 李-周法风险人口死亡率推荐

在实际计算时，式（4）通常简化为

本研究在进行计算时，对李-周法进行一定的简化，在选取死亡率时忽略其是否为夏天、晴天、白天或冬天、雨天、夜间，统一取推荐值进行初步计算。

第一,健康教育宣导。护理人员可利用医院相关宣传册、黑板报、网上视频教学等宣传手段让孕妇充分了解妊娠的具体过程,并使孕妇及其家属充分了解整个孕期中孕妇所应注意的各种问题。同时,护理人员应注意将相关分娩知识教予孕妇,让孕妇对于分娩过程有一个直观的了解,以提高孕妇顺利分娩的成功率,缓解孕妇的紧张和焦虑。此外,护理人员还应对孕妇及其家属进行血糖控制知识教育,避免并发症的产生。

3.3 生命损失估算结果

本研究选定警报时长为WT=0.25 h、WT=0.5 h、WT=1 h 和WT=2 h，采用两种方法进行溃坝生命损失估算。 李-周法分别考虑了风险人口对溃坝洪水严重性的理解程度UD模糊与明确两种情况，最终计算结果见表5。

表5 生命损失估算结果 人

两种方法估算得到的生命损失总体上偏差较大，当警报时间WT= 0.25 h，D＆M 法估算生命损失达2151人，而李-周法（UD为模糊）估算生命损失超过10 万人。 仅当警报时间较长、风险人口对洪水严重性的理解程度UD为明确时，估算结果较为接近。 通过对比以往学者采用的溃坝洪水生命损失估算案例［20］，本研究估算结果中WT≥1 h 时D＆M 法和李-周法（UD为明确）较为合理，具有一定的参考意义。

3.4 估算结果合理性分析

（1）D＆M 法考虑因素有洪水严重性、风险人口、警报时间，忽略了风险人口对洪水严重性的理解程度、溃坝气候和时间条件，估算结果与实际情况可能存在一定偏差。 但比较本研究的生命损失估算结果，D＆M法估算结果相对而言是合理的。 在资料有限的情况下D＆M 法适用性较强，结果具有一定的参考价值。

（2）李-周法在划定警报时间时，警报时间在0.25～1 h 之间，其他影响因素一定时，风险人口死亡率为定值，因此本研究选定的WT=0.5 h 与WT=1 h 估算结果相同，但是实际上警报时间越长，生命损失应当有所减少，此处计算结果是不合理的。

（3）在城市夜间照明良好、交通方便、信息传播方式多样的情况下，风险人口对溃坝洪水严重性的理解程度更偏向于“明确”，由估算结果也可以看出，李-周法中UD为模糊时，生命损失过于严重而失真，而UD为明确时估算结果相对合理。

（4）本研究为了方便估算，警报时间取统一值，而实际中溃坝洪水自上游向下演进需要一定时间，即距离坝址越远预警时间越长，因此本研究估算结果整体上是偏保守的。

4 结语

（1）城市型水库溃决时，城市内人们可以前往结构牢固、设计合理的钢筋混凝土高楼内躲避洪水，大多数建筑物会起到有效的防洪避险作用，因此在城市型水库溃坝后果估算中，风险人口死亡率和洪水严重性参数确定都应当考虑此因素，合理取值。

（2）两种方法的估算结果均表明，警报时间极大程度影响最终生命损失估算结果。 因此，应当构建科学的城市防洪预警机制，提高洪水风险和溃坝风险的识别能力，尽可能提高警报识别准确度和延长警报时间。

（3）由李-周法的两种估算结果可知，风险人口对溃坝洪水严重性的理解程度对于估算结果影响是巨大的。 应当加强大坝安全宣传教育，普及洪水避险自救相关知识，设法提高风险人口对溃坝洪水的理解程度。

（4）当WT≥1 h 时，本研究估算的最终生命损失人数D＆M 法为363 人，李-周法（UD为明确）为228人。可见由于城市型水库下游人口密集，因此水库一旦溃坝后果十分严重，应当加强防洪决策人员及水库管理人员的风险意识，认真做好平时的管理和调度工作，防止灾害的发生。