基于串级PID的机器鱼位姿控制算法
2022-07-07宋英杰唐武生
王 刚, 宋英杰,, 唐武生, 赵 强
(1. 白城师范学院 机械与控制工程学院, 吉林 白城 137000;2. 长春大学 机械与车辆工程学院, 长春 130022)
近年来, 仿生机器鱼在管道巡护和水质监测等领域应用广泛. 机器鱼的位姿(位置和方向统称为位姿)控制要求机器鱼在游动过程中, 能克服各种干扰以到达指定目标点. 位姿控制的质量直接影响仿生机器鱼循迹、 避障、 搬运和编队的完成效果. 刘安全等[1]提出了基于改进比例导引的机器鱼位姿控制算法, 将机器鱼位姿误差中的方向角项和纵坐标项用于机器鱼角速度控制律, 横坐标项和纵坐标项用于机器鱼线速度控制律, 从而实现机器鱼的位姿控制; 肖权等[2]提出了基于轨迹生成法的机器鱼位姿控制算法, 以机器鱼行为机制理论为基础, 构建起始位姿到目标位姿的距离和方向角与视线角差值组成的矢量矩阵, 以切线和圆弧长度总和最小为最优轨迹研究机器鱼位姿控制; 韩虹飞[3]根据机器鱼波动推进特性, 在目标位姿圆切线基础上添加10 cm假定后退距离, 利用切线圆与目标方向信息寻找最佳目标位置点并调整机器鱼的方向实现机器鱼的位姿控制; 李庆春[4]以目标位姿的方向线为滑模曲线, 运用模糊滑模轨迹控制法, 根据全局摄像机反馈的机器鱼位姿信息, 实时调整机器鱼的运动方向和速度, 利用实验平台原始的点到点模糊控制算法跟踪滑模曲线上的一系列虚拟目标点, 使机器鱼能够在滑模曲线上稳定运动, 最终到达目标位姿; 潘想[5]将轮式机器人稳定位姿轨迹跟踪的控制器----滑模控制算法应用到机器鱼位姿控制实验, 有效解决了其误差大、 用时长的问题; Li等[6]提出一种改进的比例导引控制算法和自抗扰控制算法相结合的高精度控制器, 将其用于机器鱼从任意位姿到目标位姿的运动; Yu等[7]利用基于无模型强化学习的控制方法实现了机器水母姿态的自主调节, 提高了结构灵活性和偏航机动性; Zheng等[8]提出人工侧线系统和惯性测量单元集成的双传感器融合方法, 利用人工神经网络实时感知流量信息, 实现机器鱼在来流中的动态运动; Cafer等[9]用CPG(central pattern generator)和模糊逻辑控制器作为机器鱼的决策机制, 提出有限状态机(finite state machine, FSM)算法, 实现机器鱼的多场景自主巡航和避障等游动性能.
仿生机器鱼依靠鱼体和鱼鳍等与水相互作用产生流体动力, 由于水环境的干扰和动力学的非线性, 因此仿生机器鱼位姿控制的精准度较低. 本文以北京大学智能仿生实验室开发的仿鲹科三关节机器鱼为研究对象, 研究仿生机器鱼的位姿控制问题.
1 三关节仿生机器鱼
三关节仿生机器鱼包括刚性头部(含静止橡胶材质胸鳍)、 柔性鱼体(3个舵机串联组成)和具有尾柄的尾鳍3个部分, 如图1所示. 机器鱼的刚性头部无动力, 可有效抵御池壁的碰撞, 内部配重片可保证机器鱼的鱼体在水中直立. 柔性鱼体由舵机、 串联金属骨架和橡胶鱼皮组成, 柔性鱼体和尾鳍通过各舵机驱动所对应的金属骨架周期性摆动使机器鱼拟合鱼体波曲线运动, 模仿真鱼借助击水产生有效的反作用力推动机器鱼前进.

图1 仿生机器鱼Fig.1 Biomimetic robotic fish
仿生机器鱼采用CPG运动控制, 通过在线调整参数, 实现其多模态游动之间的平滑过渡[10-11]. 图2为机器鱼的CPG运动控制框图[12].

图2 机器鱼的CPG运动控制框图Fig.2 CPG motion control block diagram of robotic fish
CPG控制器的数学描述[12]如下:

(1)

(2)

(3)
θi(t)=xi(t)+ri(t)sin(φi(t)),
(4)
其中i=1,2,3, 运动控制参数ri(t),xi(t)和φi(t)分别为第i个振荡器的振幅、 偏移和相位,Ri,Xi和ν分别为第i个振荡器的期望幅值、 期望偏移和期望频率,φij为振荡器i和振荡器j之间的期望相位差,θi为第i个振荡器对应关节的输出角,α′,β′,μ为系统结构参数, 决定系统的收敛速度,N为振荡器的总数, 对应机器鱼的3个摆动关节. CPG模型的输出为各关节对应的周期性变化摆角值, 经STM32核心板解析为驱动舵机的脉冲宽度调制(pulse width modulation, PWM)波信号. 在线调节CPG网络模型间的连接权值参数以实现各关节之间的协调运动, 使机器鱼自然协调游动.
2 位姿误差模型


图3 机器鱼位姿误差模型坐标系Fig.3 Posture error model coordinate of robotic fish

(5)


图4 机器鱼位姿控制模型流程Fig.4 Flow chart of posture control model of robotic fish
3 串级PID控制算法
位姿控制算法具有一定的局限性, 需假设机器鱼在前进过程中无障碍及目标位姿在水环境的干扰下相对固定等. 为减少水环境干扰及时延对机器鱼位姿控制精度的影响, 提高机器鱼的适应能力, 对其位姿控制采用串级控制系统, 串级比例-积分-微分(PID)控制系统结构如图5所示. 串级PID控制系统由两个PID控制器串联组成, 将外环PID控制器的输出作为内环PID控制器的输入, 内环PID控制器的输出作为控制量[16].Gc1(s)和Gc2(s)分别为主调节器传递函数和副调节器传递函数,G1(s)和G2(s)分别为主对象特性和副对象特性, 所处外环和内环分别作为主回路(PID1)和副回路(PID2),D(s)为系统中存在的干扰. 先计算PID1, 再计算PID2, 控制参数的整定顺序相反.

图5 串级PID控制系统结构Fig.5 Cascade PID control system structure
机器鱼系统对基本控制通道的控制存在非线性因素且机器鱼作业环境具有时变性, 由于全局摄像机采集的机器鱼信息与实际状态信息存在实时性误差, 因此, 单级PID控制无法满足机器鱼位姿的控制精度, 采用串级PID可提高对机器鱼的位姿控制, 即将响应速度快的线速度控制器和角速度控制器作为内环, 响应速度慢的距离控制器和方向角角度控制器作为外环[17]. 基于串级PID的仿生机器鱼位姿控制原理如图6所示.

图6 基于串级PID的仿生机器鱼位姿控制原理Fig.6 Posture control principle of biomimetic robotic fish based on cascade PID
3.1 角速度控制器设计
角速度控制器的外环角度PID控制器和内环角速度PID控制器均采用增量式PID算法, 角速度控制器的外环角度PID控制器的输入为实际方向角与期望方向角的角度误差和视线角之和, 外环角度PID控制器的输出为
其中:eθ(k)=θr-θc(k)+θs(k),θr-θc(k)为机器鱼期望方向角与实际方向角之间的差值,θs(k)=arctan[(yr-yc(k))/(xr-xc(k))]为机器鱼的视线角;kpo1,kio1和kdo1分别为角速度控制器的外环角度PID控制器的比例、 积分和微分系数;k为采样时刻.
以外环角度PID控制器的输出为内环角速度PID控制器的输入, 内环角速度PID控制器的输出为
其中:ew(k)=wr(k)-wc(k),wc为多水下机器人协作控制系统平台的全局摄像机采集的机器鱼角速度信息;kpi1,kii1和kdi1分别为角速度控制器的内环角速度PID控制器的比例、 积分和微分系数,k为采样时刻.
3.2 线速度控制器设计
线速度控制器的外环距离PID控制器和内环线速度PID控制器均采用增量式PID算法, 线速度控制器的外环距离PID控制器的输入为实际位置与期望位置的距离误差, 外环距离PID控制器的输出为

以外环距离PID控制器的输出为内环线速度PID控制器的输入, 线速度控制器的内环线速度PID控制器的输出为
其中:ev(k)=vr(k)-vc(k),vc为多水下机器人协作控制系统平台的全局摄像机采集的机器鱼速度信息;kpi2,kii2和kdi2分别为线速度控制器的内环线速度PID控制器的比例、 积分和微分系数.
受舵机和鱼皮等硬件结构的约束, 实验中所用的机器鱼巡游和机动能力有限, 仅能完成左右转弯和向前直游等动作, 不能向后倒游和达到目标位姿后立即静止. 基于串级PID的仿生机器鱼位姿控制算法中, 角速度指令和线速度指令连续, 由于在多水下机器人协作控制系统平台中, 基本控制通道已固化为有限的档位, 因此需将角速度指令和线速度指令进行离散化处理, 即分别将某个区间内的角速度指令和线速度指令变换为对应的速度档和方向档.
4 仿真结果与分析
4.1 仿真结果
在保证验证算法的有效性前提下, 尽可能减少仿生机器鱼下水次数, 避免机械疲劳以完成机器鱼位姿控制算法中控制参数的整定. 以URWPGSim2D环境下的非对抗性二维仿真花样游泳竞赛项目的6号仿真机器鱼为验证位姿控制算法的模型. 为便于区分, 将6号仿真机器鱼的颜色设置为绿色, 其中1号黄色仿真机器鱼可随机在场地游动, 不受策略控制. 为防止其他仿真机器鱼对6号机器鱼运动干扰, 将剩余红色仿真机器鱼置于左上角, 且不赋予任何动作, 即除碰撞外处于静止状态, 如图7所示. 坐标系定义为: 以仿真场地中心为原点,x轴向右,z轴向下, 负x轴顺时针转回负x轴角度范围为[-π,π].策略编写系统和仿真机器鱼的运动参数以毫米为单位.

图7 URWPGSim2D环境下的仿真机器鱼模型Fig.7 Robotic fish model in URWPGSim2D simulation environment
在机器鱼的位姿控制中, 控制参数的选择较复杂, 由于机器鱼一直处于游动状态, 系统稳态误差影响较小, 因此最后确定积分参数.先将微分参数固定为零, 从小到大改变比例参数至满足响应速度要求, 再固定比例参数, 从小到大改变微分参数, 使机器鱼稳定游向目标位姿, 利用“控制变量法”经多次仿真实验整定得到串级PID算法的控制参数, 结果列于表1. 仿真实验任务为仿真机器鱼从初始位姿(-800 mm,500 mm,-π/2 rad)游到目标位姿(600 mm,-600 mm,π/6 rad).

表1 仿真实验控制参数
4.2 仿真分析
图8为URWPGSim2D环境下基于串级PID控制律以5 s为间隔的仿真程序视频序列图. 由图8可见, 到达目标位姿所用时间为31 s. URWPGSim2D中的PoseToPose函数称为位姿到位姿控制函数, 采用的时变反馈控制律为

图8 URWPGSim2D环境下的视频序列Fig.8 Video sequences in URWPGSim2D simulation environment
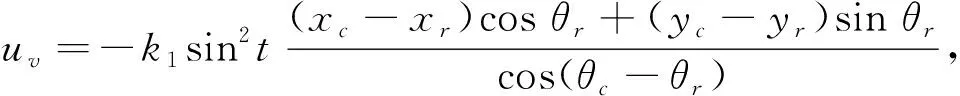
(10)
其中k1,k2和k3为时变反馈控制律的控制参数,t为时间变量.
计算相同仿真任务下时变反馈控制律与串级PID控制律仿真机器鱼位姿的绝对误差. 图9和图10分别为时变反馈控制律与串级PID控制律的位置和方向角误差对比结果. 由图9和图10可见: 仿真机器鱼采用时变反馈控制算法的误差为(29 mm,18 mm,0.111 1 rad), 到达目标位姿所用时间为27 s; 仿真机器鱼采用串级PID控制算法的误差为(7 mm,5 mm,-0.035 8 rad), 到达目标位姿所用时间为31 s. 相对时变反馈控制算法, 本文算法到达目标位姿所用时间增加, 存在角度变化跳动现象, 但位置误差和方向误差均减小, 提高了位姿控制精度, 在某些实际场合更符合应用需求.

图9 位置误差对比Fig.9 Comparison of position error

图10 方向角误差对比Fig.10 Comparison of direction angle error
5 结果与讨论
在多水下机器人协作控制系统平台下, 导入根据串级PID控制律编写的策略进行仿生机器鱼位姿控制实验, 策略编写系统和仿生机器鱼信息采集系统以像素为单位, 即用像素单位描述位置. 仿生机器鱼从初始位姿(100像素,330像素,-π/2 rad)游到目标位姿(560像素,120像素,0)作为实验任务, 以两个直径为95像素的半圆形黑色橡胶为初始点和目标点的标记点, 假设初始位姿至目标位姿途中无障碍, 机器鱼方向与x轴方向相同, 沿x轴向y轴旋转为0~π rad, 反方向旋转为0~-π rad. 多水下机器人协作控制系统中的仿生机器鱼与URWPGSim2D中的仿真机器鱼存在差异, 通过实验确定仿生机器鱼的实体实验控制参数列于表2.

表2 实体实验控制参数
目标位姿的方向角为0, 仅计算仿生机器鱼从初始位姿到达目标位姿过程中实际位姿与目标位姿之间的绝对误差. 图11为多水下机器人协作控制系统平台环境下以2 s为间隔的视频序列图.

图11 多水下机器人协作控制系统平台环境下的视频序列Fig.11 Video sequences in multi-underwater robots cooperative control system platform environment
图12~图14分别为仿生机器鱼在到达目标位姿过程中的横坐标误差、 纵坐标误差和方向角误差. 由图11~图14可见, 仿生机器鱼到达目标位姿所用时间为14.4 s, 误差为(-3像素,-4像素,0.062 rad), 基本满足仿生机器鱼的循迹和搬运等实际应用要求, 表明了算法的有效性, 由于采用固定的比例、 积分和微分参数, 因此仿生机器鱼的方向角易跳动.

图12 横坐标误差Fig.12 Abscissa error

图13 纵坐标误差Fig.13 Ordinate error
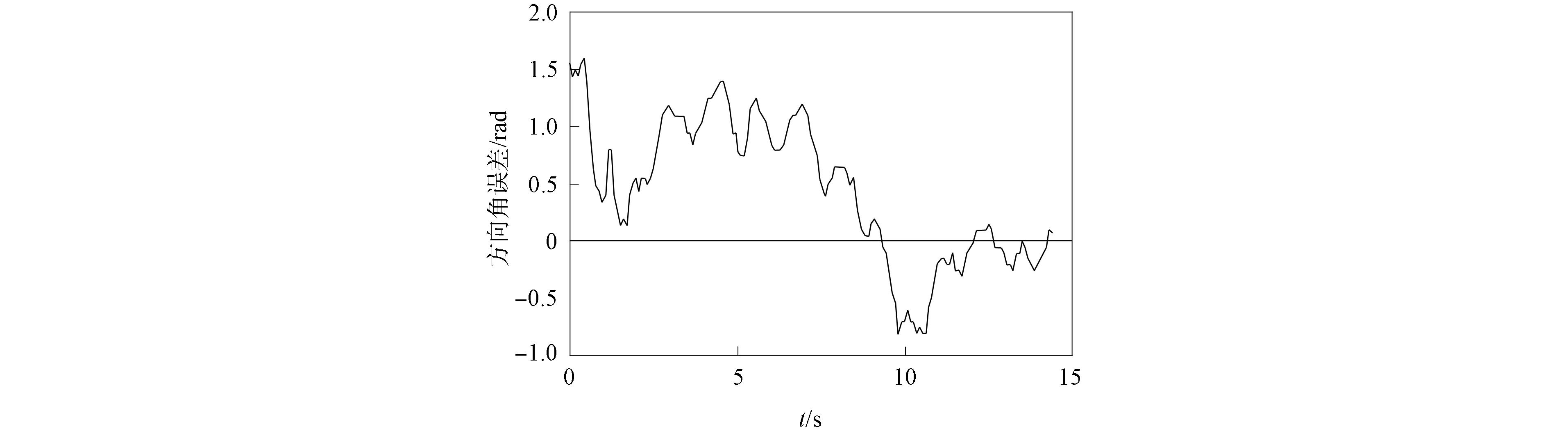
图14 方向角误差Fig.14 Directional angle error
综上, 本文基于期望位姿建立坐标系构建机器鱼的位姿误差模型, 针对机器鱼的位姿控制问题, 利用串级PID控制算法与时变反馈控制算法在URWPGSim2D环境下进行仿真实验, 仿真结果表明, 在一定的误差范围内, 与时变反馈控制律相比, 串级PID控制律达到期望位姿所用时间增加, 且存在方向角角度变化跳动现象, 但位置误差和方向误差均减小, 提高了位姿控制精度. 利用Microsoft Visual Studio 2010编写相应策略, 将其分别应用到URWPGSim2D软件的仿真平台和多水下机器人协作控制系统平台上, 证明本文算法合理且有效.
