一种基于Gray码规则的彩色图像量子隐写方案
2022-07-07陈欣燕
肖 红, 陈欣燕
(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)
量子计算[1]作为一种新的计算方法以其高度的并行性受到广泛关注, 例如量子人工智能[2]、 量子机器学习[3]和量子图像处理[4]等. 目前量子图像处理的研究主要包括两方面: 量子图像表示和量子图像处理算法. 对于量子图像表示目前已有许多方法, 如Qubit Lattice模型[5]、 Real Ket模型[6]和FRQI(flexible representation of quantum images)模型[7-8]. 这3个模型是量子图像表示的基础模型, 其他各种模型都是对这3个模型的修改或扩展. 文献[9]给出了量子图像表示的发展过程. 量子图像处理算法包括几何变换、 色彩处理、 特征提取、 图像分割、 图像置乱、 图像加密、 信息隐藏和数字水印等, 其中图像信息隐藏技术目前已成为量子图像处理领域的一个研究热点.
在灰度载体图像隐写方面, 文献[10]提出了一种基于Moire Pattern的水印算法; 文献[11]提出了一种基于LSB(least significant bit)的信息隐藏算法; 文献[12]提出了两种盲LSB隐写算法, 一种使用消息位直接代替像素的LSB, 另一种将消息位嵌入到一个图像块的多个像素中; 文献[13]提出了一种同时采用LSB和MSB(most significant bit)的量子隐写算法, 该算法实际上只有50%秘密信息嵌入到载体图像中, 其余50%作为密钥. 上述算法的嵌入容量均不超过每像素1 bit. 文献[14]提出了一种基于Arnold置乱和LSB的隐写算法, 该算法将经Arnold置乱后的图像嵌入到载体的图像LSB中, 嵌入容量达到每像素2 bit. 在彩色载体图像隐写方面, 文献[15]提出了一种量子图像LSB信息隐藏算法, 虽然该方法的嵌入容量达到每像素3 bit, 但其安全性较低; 文献[16]研究了3种基于LSB的量子彩色图像隐写算法, 其中前两种嵌入容量为每像素1 bit, 第三种为每像素2 bit; 文献[17]提出了一种新的基于量子LSB的彩色图像Gray码隐写方法, 该方法中Gray码的优势并未得到充分利用, 且嵌入容量仅为每像素2 bit.
针对上述问题, 本文提出一种新的彩色载体图像量子隐写算法. 该算法将秘密信息划分为多个3 bit段, 每个3 bit段根据其自身的值和Gray码映射规则嵌入到载体图像的LSB中. 最后采用不同的秘密图像和载体图像作为实验对象, 并与其他方法进行对比, 结果表明, 该算法在嵌入容量和安全性方面均有提升.
1 预备知识
1.1 彩色图像的量子表示
本文基于QRMW(quantum representation of multi wavelength images)提出一种新的彩色图像量子表示方法, 该模型同样使用3组纠缠量子位序列, 分别对每个像素的颜色、 通道、 位置信息进行编码. 第一量子位序列用于编码像素的颜色值, 需要8个量子比特; 第二量子位序列用于编码RGB通道, 需要2个量子比特, 这2个量子比特处于3个基态|00〉,|01〉,|10〉(分别表示R,G,B三通道)的均衡叠加态中, 量子线路如图1所示; 第三量子位序列用于编码像素位置.

图1 2个量子比特产生3个均衡叠加态的量子线路Fig.1 Quantum circuits that two qubits produce three equilibrium superposition states
因此描述一个大小为2n×2n、 颜色范围为(28,28,28)的彩色图像, 仅需要(2n+10)个量子比特.一张2n×2n的彩色图像可表述为
其中
一张2×2的彩色图像及其对应的量子描述如图2所示.

图2 一张2×2的彩色图像及其模型的表示方式Fig.2 Color image of 2×2 and its model representation
1.2 Gray码及其在LSB隐写中的应用
在Gray码中, 任何两个相邻的代码只有一个不同的二进制数. 此外, 由于最大码与最小码之间只相差一位数字, 即首尾相连, 因此它也被称为循环码或反射码[18].
二进制码bnbn-1,…,b1与其Gray码gngn-1,…,g1之间的相互转换[18]为

(2)

(3)
以4位Gray码为例(其他情况类似), 实现二进制码和Gray码转换的量子线路如图3所示.

图3 实现二进制码和Gray码互相转换的量子线路Fig.3 Quantum circuits that implement conversion between binary code and Gray code
文献[18]研究了Gray码在LSB图像隐写中的应用, 采用灰度图像作为载体, 按照Gray码规则嵌入秘密信息. 该方案的优点是其遵循变换规则, 隐写图像的LSB并不总等于秘密位, 实验结果表明二者的差异几乎达到50%. 但其嵌入容量仅为每像素1 bit.
2 彩色图像的量子隐写算法
本文提出的隐写方案包括分割、 嵌入、 提取和恢复4个过程, 如图4所示.

图4 本文隐写方案的流程Fig.4 Flow chart of proposed steganography scheme
2.1 秘密图像的像素比特分段
为便于描述, 本文中秘密信息(即需要嵌入载体彩色图像|CI〉中的信息)是指大小为2u×2v且灰度范围为28的灰度图像|SI〉.将秘密消息嵌入载体图像的基本思想: 首先将|SI〉中的量子比特序列视为3 bit段序列, 然后将每段嵌入到载体像素RGB通道的LSB中, 如果最后一段小于3 bit, 则用对应位置载体图像的像素比特填充. 因此, 为将|SI〉嵌入到大小为2n×2n的|CI〉中, 首先需要将|SI〉转换成大小为2u+v+2-n×2n、 灰度范围为23的图像, 其中u+v+2≤2n.分段后的秘密图像与载体图像的列数相同, 行数小于等于载体图像的行数.经过像素比特分段后的秘密图像通常含有一些冗余像素, 本文将这些冗余像素的灰度值设为|0〉.下面给出一个嵌入实例.
假设载体图像的大小为4×4, 原始秘密图像大小为2×2, 则秘密图像包含2×2×8=32个秘密比特, 这些秘密比特可视为11个3 bit段, 其中最后1位段只有2 bit, 此时可用载体图像对应位置的像素比特填充. 这11个3 bit段可视为一个大小为3×4且灰色范围为23的图像, 显然需要4 bit实现位置编码, 因此会导致有5个冗余像素, 如图5所示.

图5 一个原始秘密图像及其分割后图像的实例Fig.5 An example of original secret image and its segmented image
2.2 秘密图像的嵌入过程

图7 在载体图像中嵌入单个秘密像素的量子线路Fig.7 Quantum circuits for embedding a single secret pixel in carrier image
2.3 秘密图像的提取过程
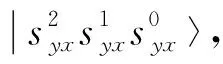
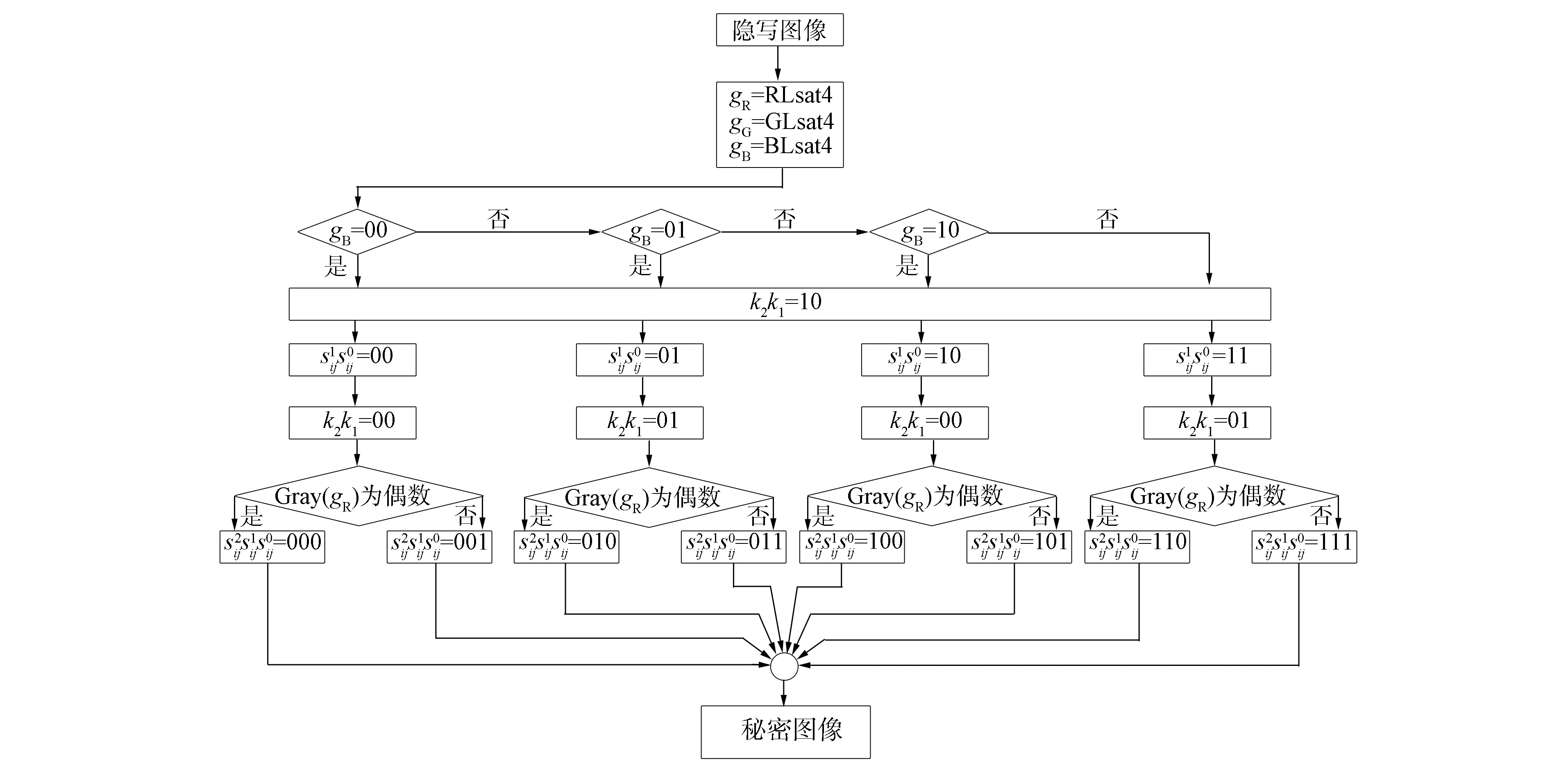
图8 秘密图像的提取方案Fig.8 Extracting scheme of secret image

图9 在载体图像中提取单个秘密像素的量子线路Fig.9 Quantum circuits for extracting a single secret pixel in carrier image
为便于理解, 本文给出一个实例, 它描述了3个秘密比特是如何嵌入到一个载体像素并提取出来的. 假设载体像素的三通道颜色值为
P=(|rij〉,|gij〉,bij〉)=|01100110〉 |10110101〉|00110011〉,


3 复杂度分析
在量子图像处理中, 量子线路的复杂性主要根据通用逻辑门(Hadamard门, 非门, 受控非门(Controlled-NOT gate, CNOT)以及任意2×2酉算子)的数量决定. 下面从分析每个子模块的复杂性开始, 逐步确定整个线路的复杂性.
1) 量子比较器、 Gray码的转换. 由文献[19]可知, 量子比较器的复杂度不超过O(n2), 由图2可知, Gray码转换的复杂度为O(3).
2) 秘密图像的像素分段.该线路由2u+v+3个(2u+2v+3)-CNOT门组成.根据文献[20], 一个k-CNOT门可由(4k-8)个2-CNOT门和一些辅助比特实现.由u+v+2≤2n可知, 该模块的复杂度不超过O(22n+1n).
3) 嵌入单个秘密像素线路. 由图7可知, 该线路由两个Gray码转换、 9个Toffoli门、 8个6-CNOT门、 16个5-CNOT门组成, 因此该线路的复杂度为与图像大小无关的常数.
4) 秘密图像嵌入线路. 该量子电路由两个量子比较器和一个单像素嵌入模块组成, 因此该线路的复杂度不超过O(n2).
5) 提取单个秘密像素线路.由图9可知, 该线路由两个Gray码转换、 8个Toffoli门和4个3-CNOT门组成, 因此该线路复杂度也为与图像大小无关的常数.
6) 秘密图像提取线路. 该线路由两个量子比较器和一个单像素提取模块组成, 因此这种电路的复杂度不超过O(n2).
7) 秘密图像恢复.该线路的复杂度与秘密图像分段线路相同.
因此, 如果不考虑秘密图像的像素分段和恢复过程, 则隐写方案的复杂度不超过O(n2); 如果考虑所有过程, 则复杂度为O(22n+2n+n2).
4 经典计算机上的仿真实验与分析
由于目前量子计算机尚未普及, 因此在经典计算机上对几种彩色图像的隐写方案进行仿真.仿真硬件环境为配置Intel(R)Core(TM)i7-10700CPU@2.90 GHz, 8.00 GB RAM和64位Win10操作系统的台式计算机. 软件环境为MATLAB2019a. 为验证本文隐写方案的优点, 将本文方案与文献[15-17]中的隐写方案进行比较. 仿真中使用4个512×512的彩色载体图像如图10所示.

图10 实验中使用的4张载体图像Fig.10 Four carrier images used in experiments
由于文献[16]和文献[17]的嵌入容量是每像素2 bit, 即最多可嵌入512×512=256×256×4个秘密比特, 因此嵌入的秘密图像最大为256×256. 同理, 文献[15]和本文中的隐写方案嵌入容量为每像素3 bit, 即最多可嵌入512×512×3=384×256×8个秘密比特, 因此嵌入的秘密图像最大为384×256. 两个大小为256×256和两个大小为384×256的灰度图像(作为秘密图像)如图11所示.

图11 实验中使用的4张秘密图像Fig.11 Four secret images used in experiments
4.1 4种隐写方案的PSNR比较
令C是大小为2n×2n的彩色载体图像,S是嵌入秘密信息后的隐写图像, 则PSNR可定义为

(4)
将图10中的4张载体图像分别嵌入图11中的4张秘密图像后, 本文方案和其他3种方案的PSNR对比结果列于表1. 由表1可见, 当嵌入相同大小的秘密图像后, 与其他方案相比, 本文方案的PSNR仅降低了0.5~3 dB. 当达到最大嵌入容量时, 与文献[16]和文献[17]的方案相比, 虽然PSNR降低了2~4 dB, 但嵌入容量增加了1/3; 与文献[15]的方案相比, 虽然PSNR降低了约3 dB, 但后续实验结果表明, 本文嵌入方案更安全. 此外, 本文方案在达到最大嵌入容量后, PSNR值仍大于48 dB, 这在一般情况下可以接受.

表1 秘密图像和载体图像不同组合下4种隐写方案的PSNR对比
将图11(C)中的秘密图像嵌入到所有载体图像中, 该方案的视觉效果如图12所示. 由图12可见, 原始的载体图像和对应的隐写图像仅用肉眼无法区分, 这也在一定程度上验证了本文方案的安全性.

图12 秘密信息嵌入载体图像前后的视觉效果Fig.12 Visual effect before and after secret information is embedded into carrier image
4.2 直方图分析
图13为两张原始载体图像和嵌入图11(B)中秘密图像后的隐写图像直方图. 由图13可见, 与原始载体图像的直方图相比, 虽然隐写图像的直方图有轻微抖动, 但仍保持了高度的一致性.

图13 隐写图像的直方图Fig.13 Histogram diagram of steganography images
4.3 安全性


图14 两种方案直接提取隐写图像中RGB三通道的LSB得到的秘密图像Fig.14 Secret images obtained by directly extracting LSB of RGB three-channel in steganography image for two schemes

(5)



表2 原始秘密图像与直接提取隐写图像的LSB得到的秘密图像相似性
由表2可见, 对于不同载体图像和秘密图像的组合, 本文方案的相似度为0.498 1~0.500 9, 因此具有更好的安全性. 对于文献[15]的方案, 提取的图像与原始秘密图像完全相同(即相似度等于1), 因此根本不存在安全性.
4.4 鲁棒性
为评估该隐写方案在信道噪声情况下的鲁棒性, 本文分别考察了3种噪声: 均值为0、 方差为0.01的高斯噪声; 密度为0.1的椒盐噪声; 翻转概率为0.01的量子比特翻转噪声. 首先在隐写图像中分别混入上述3种噪声中的一种, 然后考察秘密图像的提取效果, 并将本文方案与文献[15-17]的方案进行比较, 进一步验证本文方案的有效性.
仿真结果表明, 几种方案的鲁棒性能相似. 对椒盐噪声和量子比特翻转噪声都具有良好的适应性, 而对高斯噪声的鲁棒性较差. 为定量比较4种方案的鲁棒性, 定义两张图像间的相关系数为

(6)
其中E(x)和D(x)分别为图像x像素灰度值的数学期望和方差.
利用式(6)将x作为原始秘密图像,y作为从叠加噪声的隐写图像中提取的秘密图像.4种方案在不同噪声下的相关系数比较分别列于表3~表5.

表3 4种方案在高斯噪声下的相关系数比较
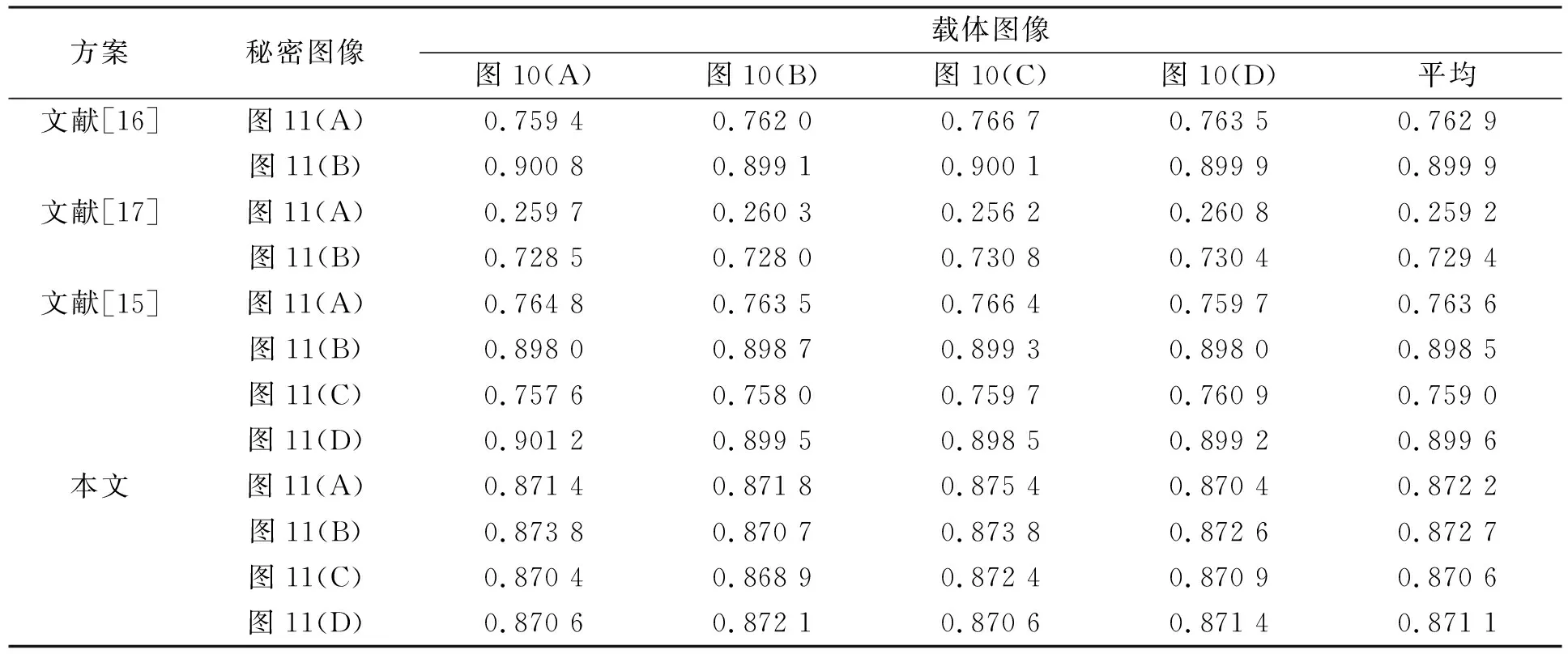
表4 4种方案在椒盐噪声下的相关系数比较

表5 4种方案在量子比特翻转噪声下的相关系数比较
由表3~表5可见: 4种方案对高斯噪声的鲁棒性较差; 对椒盐噪声和量子比特翻转噪声, 本文方案的鲁棒性与文献[15]和文献[16]中方案大致相同, 优于文献[17]中方案.
4.5 嵌入容量
对于隐写方案的嵌入容量, 文献[10]将其定义为秘密图像量子比特数与载体图像像素数之比:

(7)
根据该定义, 本文方案的嵌入容量为C=(3×2n×2n)/(2n×2n)=3 bit/像素. 文献[15]中方案的嵌入容量为3 bit/像素, 而文献[16]和文献[17]中方案的嵌入容量仅为2 bit/像素. 由上述实验结果可见, 本文方案不仅具有可接受的峰值信噪比、 较高的嵌入容量和更好的安全性, 而且在存在信道噪声的情况下具有更好的鲁棒性能.
综上所述, 隐写是一种在数字媒体(如数字图像、 音频或视频)中隐藏秘密信息的科学, 在经典计算机上已进行了较深入的研究, 而关于量子计算机的类似研究报道较少. 本文给出了基于LSB替代的彩色图像隐写在量子计算机上的实现方案, 该方案不直接用秘密比特替换载体图像的LBS, 而是通过Gray码规则将秘密信息间接嵌入到载体像素的LBS中, 提高了隐写图像的安全性. 与现有的几种彩色图像量子隐写方案相比, 该方案不仅具有可接受的峰值信噪比, 较高的嵌入容量和更好的安全性, 而且在存在信道噪声的情况下具有更好的鲁棒性.
