基于经典线性码构造的纠缠辅助量子码
2022-07-07林晶晶唐西林
林晶晶, 唐西林
(华南理工大学 数学学院, 广州 510640)
量子纠错码在量子信息和量子计算中具有重要作用. 目前, 关于量子码[1-2]的研究已得到广泛关注. 许多具有良好参数的量子码都是由包含其Euclide对偶码的经典线性码构造的. Brun等[3]提出了一种简单而基本的量子码, 称为纠缠辅助量子码(简称EAQECC). 通过放松对偶性条件并增加量子纠缠辅助位, 可从经典线性码(包括对偶包含和非对偶包含的经典线性码)出发构造纠缠辅助量子码. 这些纠缠辅助量子码具有纠缠辅助和量子纠错的双重优点. 此外, 纠缠辅助量子码可从任意的经典码中通过共享量子纠缠比特得到. 近年来, 对纠缠辅助量子码的构造研究得到广泛关注, 已构造了各种不同类型的纠缠辅助量子码[4-8]. 文献[9]利用常循环码构造了参数较灵活的纠缠辅助量子码; 文献[10-11]利用广义RS(Reed-Solomon)码构造了具有灵活参数c的新的纠缠辅助量子MDS(maximum-distance-separable)码. 本文通过经典的线性码构造码长和最小距离更灵活的两类纠缠辅助量子码.
1 预备知识

假设C是Fq上长度为n的线性码, 则C的Euclide对偶码定义为
若C满足C⊥⊆C, 则称C为Euclide对偶包含码; 若C满足C⊆C⊥, 则称C为Euclide自正交码; 若C满足C=C⊥, 则称C为Euclide自对偶码.称C∩C⊥为C的Euclide Hull, 记为Hull(C).
GRS(generalized Reed-Solomon)码是常被用于构造纠缠辅助量子码的经典线性码.假设a1,a2,…,an是Fq上n个不同的元素,v1,v2,…,vn是Fq上n个非零元素, 则关于向量a=(a1,a2,…,an)和v=(v1,v2,…,vn)的GRS码定义为
GRSk(a,v)={(v1f(a1),v2f(a2),…,vnf(an)):f(X)∈Fq[X]k},
其中Fq[X]k表示Fq上所有次数小于k的多项式集合.选取Fq[X]k的一组基{1,x,…,xk-1}, 则GRSk(a,v)的生成矩阵为
GRSk(a,v)是一个参数为[n,k,n-k+1]q的MDS码.
定义1[12]假设C是Fq上的一个线性码, 若Hull(C)=C∩C⊥={0}, 则称C为Fq上的一个线性互补对偶(linear complementary dual)码, 简称LCD码.
性质1[12]假设C是Fq上的一个线性码, 并且G和H分别为C的一个生成矩阵和校验矩阵, 则下列性质等价:
1)C是一个LCD码;
2) 矩阵GGT非奇异;
3) 矩阵HHT非奇异.
性质1给出了LCD线性码与线性码的生成矩阵和校验矩阵之间的关系.
Wilde等[13]证明了纠缠辅助量子码可由经典的线性码构造, 得到如下结果.
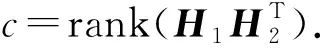
下面引入纠缠辅助量子码的Singleton界.
性质3[3]一个参数为[[n,k,d;c]]q的纠缠辅助量子码满足:
n+c-k≥2(d-1),
其中0≤c≤n-1.
如果一个参数为[[n,k,d;c]]q的纠缠辅助量子码能达到纠缠辅助量子Singleton界, 即2(d-1)=n-k+c, 则该纠缠辅助量子码称为极大距离可分纠缠辅助量子码, 简称MDS EAQECC.如果c=n-k, 则该纠缠辅助量子码称为极大纠缠的纠缠辅助量子码.
性质4[8]假设C是一个参数为[n,k,d]q的线性码, 并且H和G分别是C的校验矩阵和生成矩阵, 则
rank(HHT)=n-k-dim(HullE(C))=n-k-dim(HullE(C⊥)),
rank(GGT)=k-dim(HullE(C))=k-dim(HullE(C⊥)).
性质4表明, rank(HHT)独立于线性码C的校验矩阵H, 且可通过HullE(C)的维数求得.
2 构造第一类纠缠辅助量子码
下面将构造一些新的纠缠辅助量子码.假设C是一个参数为[n,k,d]q的经典线性码,h∶=dim(HullE(C)),M(Fq,k×k)表示由Fq上k×k矩阵构成的集合.
情形1)q=pe, 其中p为奇素数,e≥1为正整数.
引理1[14]假设q是一个奇素数幂, 则对任意的对称矩阵A∈M(Fq,k×k), 存在一个非奇异矩阵Q∈M(Fq,k×k), 使得QTAQ是Fq上的k×k阶对角矩阵, 即QTAQ=diag{λ1,λ2,…,λk}, 其中λi∈Fq, 1≤i≤k.
下面给出一种利用引理1获得LCD线性码C的一组正交基方法.
引理2假设q是一个奇素数幂,C是一个参数为[n,k]q的LCD线性码, 则存在C的一组基{c1,c2,…,ck}, 使得对任意的i,j∈{1,2,…,k}, 均有
证明: 假设G是码C的一个生成矩阵.由于C是一个LCD码, 则由性质1可知GGT是Fq上k×k阶非奇异对称矩阵.再根据引理1可知: 存在一个非奇异矩阵N∈M(Fq,k×k), 使得
NGGTNT=NG(NG)T=diag{λ1,λ2,…,λk},


引理3假设C是一个参数为[n,k]q的经典线性码, 0 证明: 假设B={c1,c2,…,ch}是线性码HullE(C)的一组基, 将B扩充成为线性码C的一组基{c1,c2,…,ch,ch+1,…,ck}. 因此,x∈C⊥. 由于x∈C⊥,x∈C′⊆C, 因此x∈HullE(C).又因为Hull(C)∩C′={0}, 所以x=0.于是C′是一个参数为[n,k-h]q的LCD码.证毕. 综上所述, 首先可通过引理3找到经典线性码C的一个参数为[n,k-h]q的LCD线性子码C′, 然后再通过引理2找到线性子码C′的一组正交基, 最后利用这组正交基可构造具有如下参数的新的纠缠辅助量子码. 命题1假设q=pe>3,p是一个奇素数, 并且C是一个参数为[n,k,d]q的经典线性码, 记h∶=dim(HullE(C)), 则对于满足0≤l≤k-h的任意l, 均存在一个参数为[[n+l,k-h,d′;n-k-h+l]]q的纠缠辅助量子码, 这里d≤d′≤d+l. 证明: 1) 当l=0时, 根据性质2和性质4, 结论显然成立. 2) 首先考虑1≤l≤k-h并且h>0. 如果h>0, 则根据引理3, 存在C的一个线性子码C′, 使得C′是一个参数为[n,k-h]q的LCD码.再根据引理2, 存在C′的一组基{x1,x2,…,xk-h}, 使得对于任意的i,j∈{1,2,…,k-h}, 均有 其中H是码C的校验矩阵.此时 其次, 当h=0时,C是LCD码, 结论仍成立. 由命题1可得: 推论1假设q=pe>3,p是一个奇素数, 并且C是一个参数为[n,k,d]q的Euclide对偶包含线性码, 即C⊥⊆C, 则对于满足0≤l≤2k-n的任意c, 均存在一个参数为[[n+l,2k-n,d′;l]]q的纠缠辅助量子码, 这里d≤d′≤d+l. 推论2假设q=pe>3,p是一个奇素数, 并且Ck是Fq上一个参数为[q,k,q-k+1]q的GRS码, 其中a=(a1,a2,…,aq),a1,a2,…,aq是Fq上q个不同的元素,v=(1,1,…,1), 则对于1≤k≤q-1且2k>q, 存在一个参数为[[q+1,2k-q,q-k+2;1]]q的MDS纠缠辅助量子码. 情形2)q=2. 定理1[15]假设A∈M(F2,k×k)是秩为t的对称矩阵, 则: 1) 如果A的所有对角元素都为0, 则t为偶数, 并且存在一个非奇异矩阵Q∈M(F2,k×k), 使得 2) 如果A的对角元素至少有一个不为0, 则存在一个非奇异矩阵Q∈M(F2,k×k), 使得 利用定理1, 可对F2上的LCD线性码C的生成矩阵分两类进行讨论, 进而对不同类的生成矩阵可得到相对应的两类不同的基. NGGTNT=NG(NG)T=diag{1,1,…,1}. 假设G′=NG, 则G′也是码C的一个生成矩阵.用ci表示矩阵G′的第i行, 这里1≤i≤k.由于 G′G′T=NG(NG)T=diag{1,1,…,1}, 因此{c1,c2,…,ck}即为希望得到的一组基.证毕. 于是, 首先可通过引理3找到经典线性码C的一个参数为[n,k-h]2的LCD线性子码C′, 然后对线性子码C′的生成矩阵进行分类, 再通过引理4和引理5找到线性子码C′相对应的一组基, 最后利用找到的基构造具有如下参数的新的纠缠辅助量子码. 命题2假设C是参数为[n,k,d]2的经典线性码, 如果h=dim(HullE(C)), 则对于满足0≤l≤k-h的任意l, 均存在一个参数为[[n+l,k-h,d′;n-k-h+l]]2的纠缠辅助量子码, 其中d≤d′≤d+l. 证明: 1) 当c=0时, 根据性质2和性质4, 结论显然成立. 2) 考虑1≤l≤k-h且h>0. 根据引理4, 存在C′的一组基{x1,x2,…,xk-h}, 使得对于任意的i,j∈{1,2,…,k-h}, 均有 (i) 当l=1时, 此时有 (iii) 当l=2或l≥4时, 其中 此时有 (i) 当l=1时, 此时有 (ii) 当l=2时, 此时有 由命题2可得: 推论3假设C是一个参数为[n,k,d]2的Euclide对偶包含线性码, 即C⊥⊆C, 则对于任意的0≤l≤2k-n均存在一个参数为[[n+l,2k-n,d′;l]]2的纠缠辅助量子码, 这里d≤d′≤d+l. 推论4假设C是一个参数为[2n,2n,1]2的线性码,C的生成矩阵为E2n, 则存在一个参数为[[2n+1,2n,2;1]]q的纠缠辅助量子码. 命题3假设q≥2是一个素数幂,C是一个参数为[n,k,d]q的Euclide对偶包含线性码, 即C⊥⊆C, 则对于满足l≤n-k的任意l, 均存在一个参数为[[n+l,2k-n+l,d′;2l]]q的纠缠辅助量子码, 这里d≤d′≤d+l. 综上可见, 从基于Euclide对偶包含线性码的对称量子码的CSS构造[16-17]出发, 当且仅当存在一个Euclide对偶包含线性码[n,k,d]q时, 可以构造一个参数为[[n,2k-n,d]]q的量子码.结合上述命题可知, 如果存在一个参数为[[n,2k-n,d]]q的量子码, 则可构造出具有下列参数的纠缠辅助量子码: 1) [[n+l,2k-n,d′;l]]2, 其中0≤l≤2k-n,d≤d′≤d+l; 2) [[n+l,2k-n+l,d′;2l]]q, 其中l≤n-k,d≤d′≤d+l.

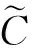
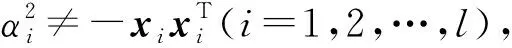


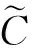










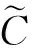

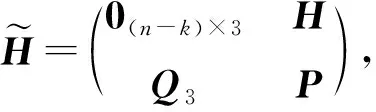


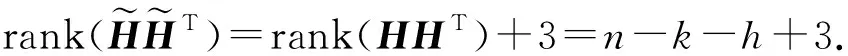














3 构造第二类纠缠辅助量子码