基于改进鲸鱼算法的长江经济带配送问题研究
2022-07-07朱光福朱云波
朱光福 朱云波
(重庆城市管理职业学院商学院 重庆 401331)
0 引 言
长江经济带统辖11个省市,覆盖长三角、长江中游和成渝三大城市群,横跨东部、中部和西部三大经济区,不仅幅员面积占国土面积21%,经济总量占全国45%,而且货运量占全国53%,在我国物流发展中具有显著地位[1-2]。从某种程度上讲,长江经济带物流配送问题直接影响着我国物流成本和企业竞争力。
近年来,学者们纷纷对物流配送问题进行深入研究,提出了大量求解算法。比如,文献[3]和文献[4]分别提出了求解配送路径优化问题的遗传算法(GA)和粒子群算法(PSO),文献[5]则根据配送路径优化问题的特点,对传统植物算法进行改进优化,提高了算法求解性能。分析可知,上述文献提出的智能算法,虽然一定程度上优化了配送方案,但仍然存在不足,比如:GA计算量较大,PSO进化后期容易陷入局部最优解,而且过度依赖于参数设置,这些都会对配送方案的高效性造成影响。
鲸鱼算法(Whale Optimization Algorithm,WOA)是模拟鲸鱼捕食机制而设计的一种新型智能群算法,最初由Mirjalili于2016年提出[6-7],其优点在于搜索机制简单,能够大大减少算法计算量,加快算法收敛速度;控制参数少,且参数设置情况不会对算法最终求解结果造成过大影响。其缺点在于,由于寻优机制简单,导致算法在处理一些规模较大的非线性优化问题时容易陷入局部最优解。
基于上述分析,本文对长江经济带物流配送问题的求解算法进行研究。在标准WOA中分别引入混沌机制、自适应惯性权重、蛙跳算法和模拟退火算法,提出了求解配送问题的IWOA,并利用长江经济带企业配送实例和国际标准算例对算法求解性能进行验证,为改善配送方案提供了新的思路。
1 长江经济带配送问题的数学模型
长江经济带配送问题可以描述为[8]:已知位于长江经济带的物流公司位置、配送车辆载重量、客户位置及需求量,需要在满足以下假设条件的情况下,合理安排配送线路使总体配送成本最小。
假设1:每个客户都有且只有一辆车辆进行配送。
假设2:每辆车辆均不能超载。
假设3:车辆油耗与车辆载重成正比。
假设4:物流公司拥有足够的同类型配送车辆。
pi=qi/Q
(1)
式中:qi表示车辆第i段运输路径上的实际载重;Q表示车辆最大载重;式(1)为车辆在第i段运输路径上的实载率。
(2)
式中:e1表示车辆空载情况下行驶单位距离的油耗成本;e2表示车辆满载情况下行驶单位距离的油耗成本。式(2)为第i段运输路径上车辆行驶单位距离的油耗成本。
C=si[e1+pi(e2-e1)]
(3)
式中:si表示运输距离。式(3)为车辆的总油耗成本。
根据车辆载重量和企业需求量可以预先估计为:
(4)
式中:m表示完成配送任务需要车辆数;[]表示取整函数;n表示客户数量;gi表示客户i的需求量;∂表示车辆装载系数,与装车复杂程度和车辆约束条件有关。
根据企业配送实际情况,构建以车辆固定使用成本和油耗成本最小为优化目标的车辆调度模型,设决策变量为:
则有:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
xijk(xijk-1)=0
(12)
yik(yik-1)=0
(13)
X=(xijkr)∈S
(14)
式中:0表示物流公司;F表示车辆固定使用成本;sij表示客户i到j的距离;pijk表示车辆k从客户i到j的载重率;S表示支路消去约束集合。
式(5)表示总体配送成本最小的目标函数;式(6)表示车辆k从客户i到j的载重率;式(7)表示车辆载重约束;式(8)表示每个客户由且只由一辆车配送;式(9)配送中心约束;式(10)和式(11)表示两个变量之间的关系;式(12)和式(13)表示0-1变量约束;式(14)表示消除不完整的子路径集合。
2 标准鲸鱼算法
在WOA中,鲸鱼按照螺旋方式进行捕食,主要包括包围猎物、螺旋捕猎和随机搜索三个阶段[9-10]。
2.1 包围猎物
如式(15)-式(16)所示,鲸鱼在捕食时首先会包围猎物。
D1=|CX*(t)-X(t)|
(15)
X(t+1)=X*(t)-A·D1
(16)
式中:t表示当前迭代次数;X*(t)表示历史最优鲸鱼位置向量;X(t)表示当前鲸鱼位置向量;A、C表示学习因子。
A=2α×rand-α
(17)
C=2×rand
(18)
α=2-2×t/T
(19)
式中:rand表示(0,1)之间的随机数;T表示最大迭代次数;α表示[0,2]之间线性下降的控制参数。
2.2 螺旋捕猎
鲸鱼包围猎物后,通常以螺旋方式进行捕食,对应数学模型为:
X(t+1)=X*(t)+D2·eb·rand′·cos(2π·rand′)
(20)
D2=|X*(t)-X(t)|
(21)
式中:D2表示鲸鱼和猎物之间的距离;b表示螺线形状的常数;rand′表示(-1,1)之间的随机数。实际上,鲸鱼螺旋捕猎的同时,还在不断缩小包围圈,两者是一个同步行为。如式(22)所示,假设有pi的概率选择缩小包围圈,则选择螺旋捕猎的概率则为1-pi,通常取pi=0.5。
(22)
分析可知,鲸鱼越靠近猎物,α的值就越小,A也就随之减小。由于α从2到0线性下降,所以A取值在[-α,α]之间。当A在[-1,1]之间时,鲸鱼下一个位置可以是它现在位置和猎物位置之间的任意位置。
2.3 搜索猎物
如式(23)-式(24)所示,标准WOA中,鲸鱼通过随机个体来搜索猎物:
D3=|CXrand-X(t)|
(23)
X(t+1)=Xrand-A·D3
(24)
式中:Xrand表示随机生成的位置向量。为增强算法全局寻优能力,当A≥1时,算法将随机搜索一个鲸鱼个体,并通过该个体更新其他鲸鱼位置,从而使算法跳出当前猎物,寻找更加优秀的猎物。
3 改进鲸鱼算法在长江经济带配送问题中的应用
3.1 构造解向量
对m辆车配送n个客户的路径优化问题,用m+n-1维实数向量X=(x1,x2,…,xm+n-1)表示鲸鱼个体,具体解码方式如下:
3.2 构造适应度函数
为方便算法编程,本文将车辆不能超载的约束条件整合到路径最短的目标函数中,得到算法适应度函数为:
(25)
式中:M表示非常大的正实数。分析可知,如果有任一配送车辆超载,则适应度函数值会变得很大,在算法进化过程中自然会被淘汰。
3.3 引入混沌机制
根据文献[11]可知,初始种群质量直接影响算法收敛速度和最终求解精度。标准WOA通过随机方式生成初始种群,不能保证鲸鱼个体在解空间均匀分布,对算法求解性能造成一定影响。对此,本文采取Logistic混沌映射随机生成初始鲸鱼个体,提高算法初始种群随机性和遍历性,具体公式如下所示:
Xn+1=μXn(1-Xn)n=0,1,2… 0≤μ≤4
(26)
3.4 引入自适应惯性权重
根据文献[12]可知,较大的惯性权重有利于提高算法全局搜索能力,较小的惯性权重有利于增强算法局部搜索能力。理想的惯性权重应该随着算法进化由大变小,这样就能够较好地平衡算法全局探索和局部开采能力。标准WOA中,惯性权重始终为1,一定程度降低了算法效率。因此,本文引入自适应惯性权重ω如下:
(27)
式中:f(X)表示鲸鱼X的适应度值;f(X*(1))表示第1次迭代中最优鲸鱼个体适应度值。改进后的鲸鱼个体更新公式为:
(28)
3.5 引入蛙跳算法
蛙跳算法是Eusuff和Lansey模拟青蛙觅食过程而提出的一种智能亚启发式算法[13-14],引入到标准WOA中能够有效增强算法局部寻优能力。核心思想在于,将鲸鱼种群随机分成L个子群,各子群个体根据式(29)-式(31)进行局部搜索,直到达到子群最大迭代代数为止。然后,所有子群重新融合。
Step=rand×(Xbl-Xwl)
(29)
Xwl_new=Xwl+Step
(30)
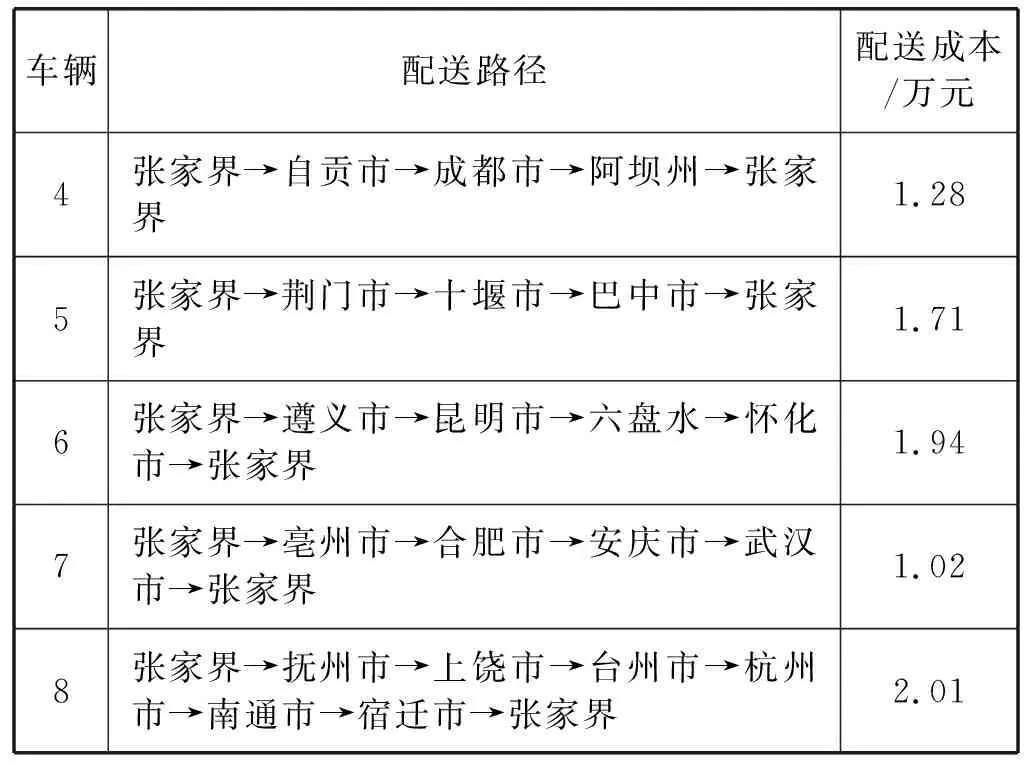
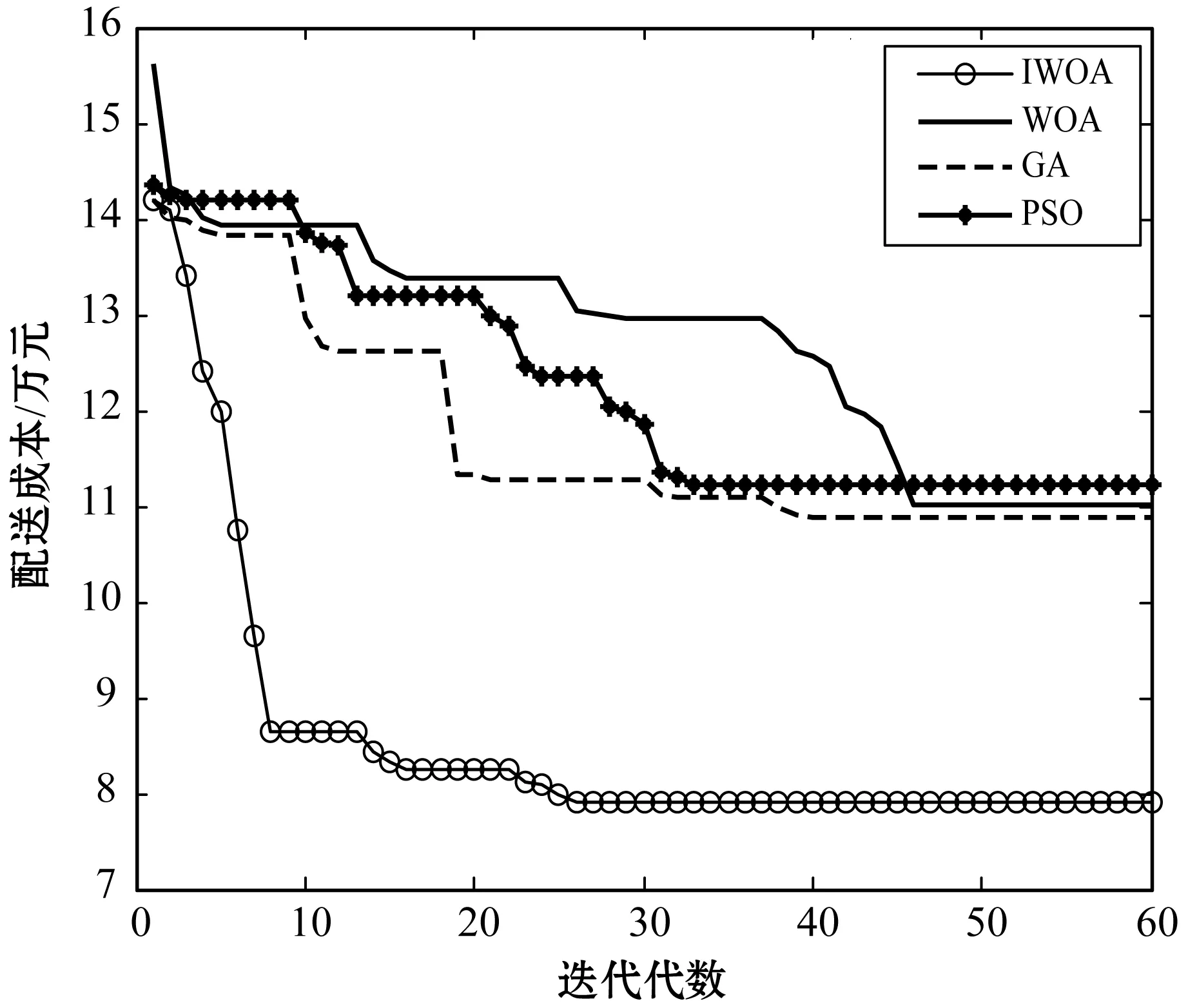
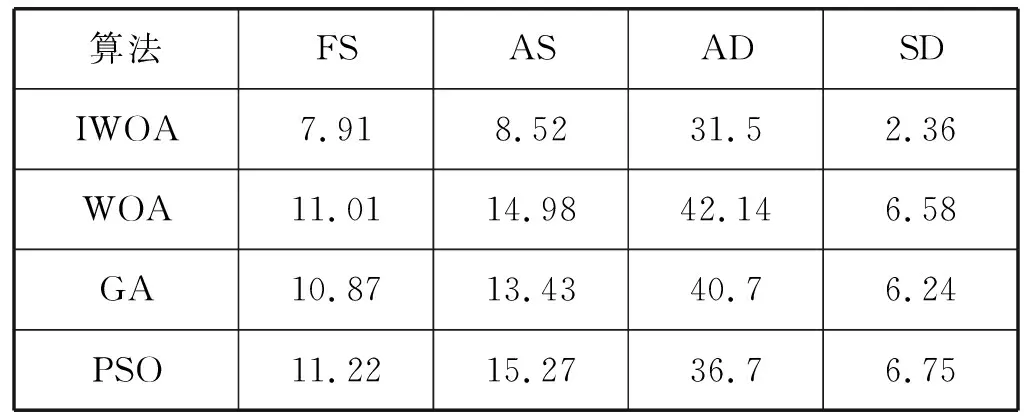
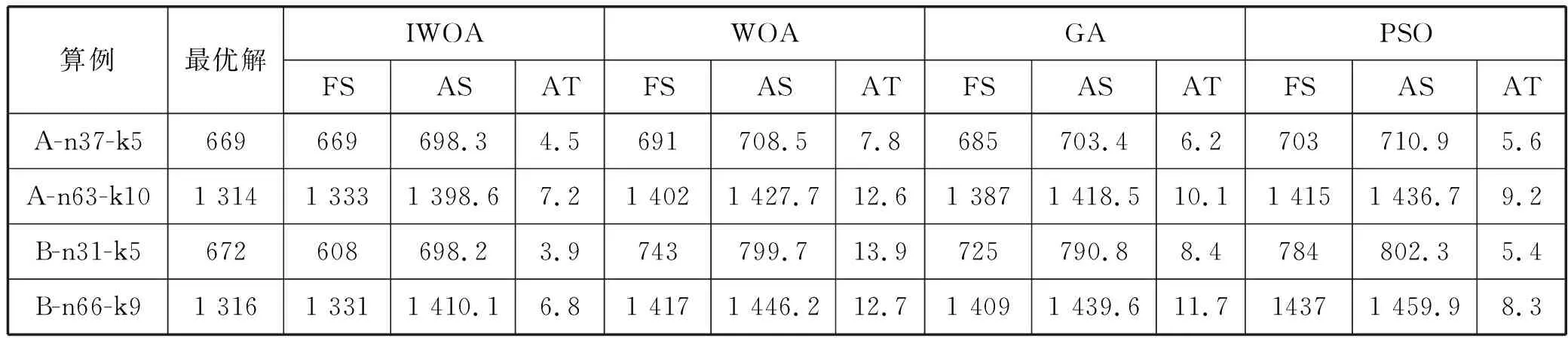
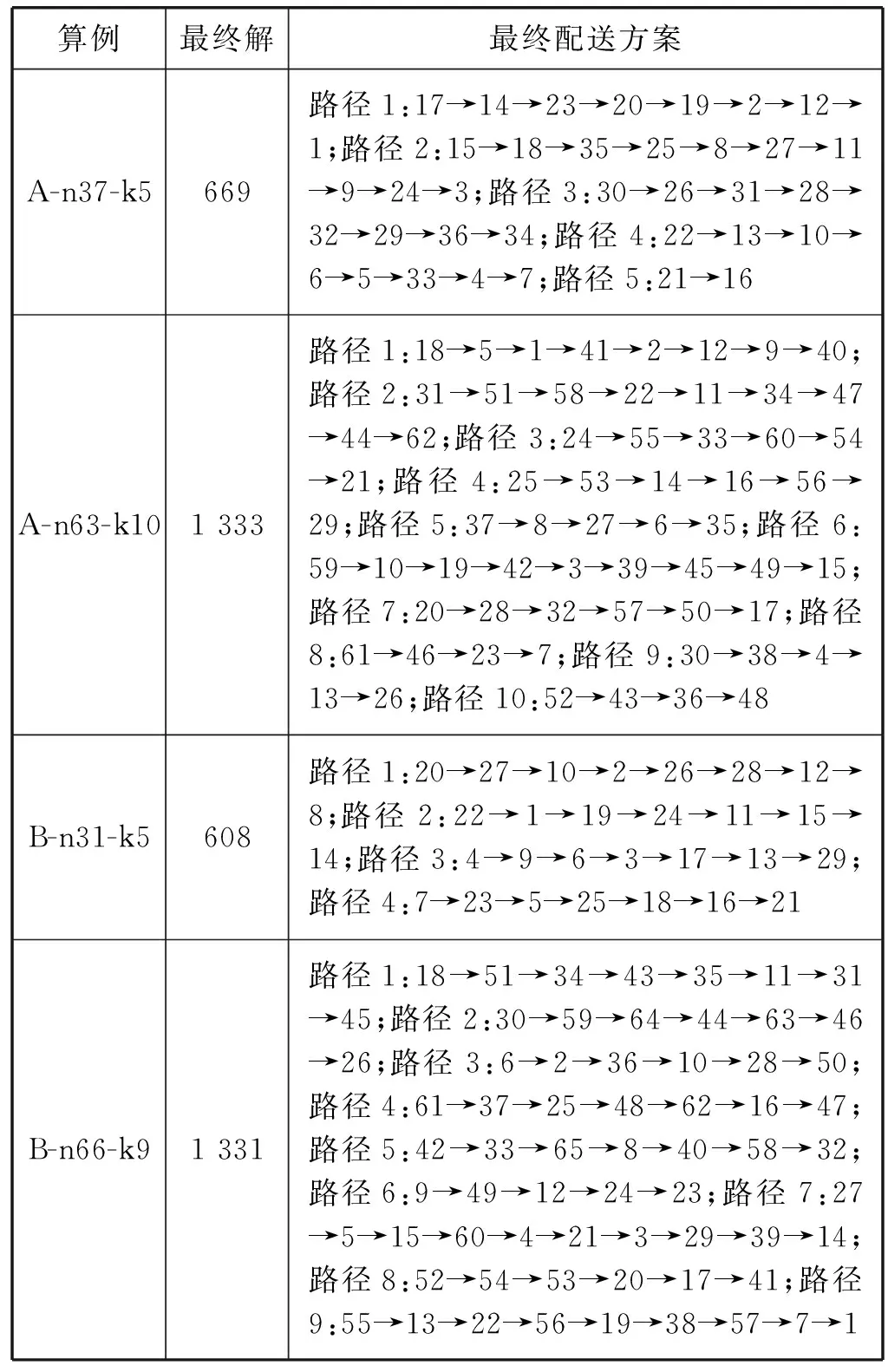
-Smax (31) 式中:Xbl、Xwl分别表示第l个子群中的最优和最差鲸鱼个体;Step表示鲸鱼局部搜索半径;Smax表示鲸鱼最大跳动步长。局部搜索后,如果f(Xwl_new) 模拟退火算法是Metropolis根据固体退火降温机制而设计的一种随机寻优算法,最大特征在于能够以一定概率接受劣质解,进而帮助算法跳出局部最优解,提高全局寻优能力[15]。所以,本文在标准WOA中针对性引入模拟退火思想,以进一步提高WOA的全局搜索能力。 根据Metropolis准则,当物体温度为Γ时,物体达到平衡的概率为exp(-ΔE/KΓ)。其中:E表示物体内能,ΔE表示内能变化量,K表示玻尔兹曼常数。根据WOA特点,本文将鲸鱼个体达到平衡的概率设置为: (32) 式中:f(X(t))表示第t次迭代中鲸鱼个体的适应度值;Γ表示第t次迭代的温度,初始温度为初始鲸鱼种群最大适应度值与最小适应度值之差。当f(X(t+1)) 根据前文所述,IWOA求解长江经济带配送问题的流程如下: 设置种群规模N、最大迭代次数T、子群最大迭代次数T1、最大跳动步长Smax等参数; 随机生成一个(0,1)之间的n+m-1维鲸鱼个体,并根据式(26)和式(27)生成其他N-1个个体,组成初始鲸鱼种群{X1,X2,…,Xi,…,XN}; 根据式(25)计算种群所有个体适应度值,将种群最优个体记为历史最优个体,同时记录模拟退火算法初始温度; while(t fori=1 toN 根据式(17)至式(19)计算A的值。 如果A≥1,根据式(23)和式(24)更新个体i位置;否则,根据式(15)、式(21)、式(27)和式(28)更新个体i位置; end for 将鲸鱼种群随机划分为规模相同的L个子群体; forl=1 toL forq=1 toT1 选出第l个子群的最优个体Xbl和最差个体Xwl; 根据式(29)-式(31)计算得到Xwl_new;如果f(Xwl_new) end for end for 将所有子群融合; fori=1 toN end for 按照Γ=0.99Γ进行退温操作; 计算种群所有个体适应度值,对比种群最优和历史最优个体适应度值,择优更新历史最优个体位置。 t=t+1 end while 输出历史最优个体,即为最优调度方案。 为验证IWOA性能,本文分别采用长江经济带企业配送实例和国际标准算例进行仿真测试。IWOA参数为:种群规模N=100、最大迭代次数T=60、子群个数L=5、子群最大迭代次数T1=20、最大跳动步长Smax=1。WOA、GA和PSO参数按相应文献设置。 已知位于张家界的物流公司(经度110.550 42°,纬度29.345 89°)要向长江经济带其他30个城市进行配送服务,各城市地理位置和需求量如表1所示。配送车辆为最大载重180 t的大型挂车,固定使用费用为F=1 230元/次,空载情况下行驶单位距离油耗成本为e1=0.56元/(km·t),满载情况下行驶单位距离油耗成本为e2=1.58元/(km·t)。 表1 长江经济带配送网络 利用IWOA对上述实例进行50次求解,最终配送方案如表2所示。 表2 IWOA最终配送方案 由表2可知,完成配送任务需要8辆车,其中车辆1为长沙市、赣州市和衡阳市3个城市服务;车辆2为武汉市、合肥市、宿迁市和亳州市4个城市服务;车辆3为安庆市、南通市、杭州市、台州市、上饶市和抚州市6个城市服务;车辆4为凉山州、丽江市和昆明市3个城市服务;车辆5为阿坝州、成都市和自贡市3个城市服务;车辆6为文山州、西双版纳、保山市和六盘水4个城市服务;车辆7为怀化市、遵义市和昭通市3个城市服务;车辆8为广安市、巴中市、十堰市和荆门市4个城市服务。所有车辆均从张家界物流公司出发,配送完成后全部返回物流公司,整体配送成本为7.91万元。 为对比验证IWOA求解性能,分别采用WOA[10]、GA[3]和PSO[4]对上述实例进行50次求解,求得最终配送方案如表3、表4和表5所示。分析可知,WOA、GA和PSO均需要8辆车才能完成配送任务,最终配送成本分别为11.01万元、10.87万元和11.22万元,均大于IWOA求解结果。如图1所示,IWOA在第27代时收敛,WOA在第45代收敛,PSO在第32代时收敛,而GA在第40代时收敛。由此可知,WOA全局寻优能力优于PSO,但也非常容易陷入局部最优解,且收敛速度慢于GA和PSO。经过本文改进后,IWOA全局寻优能力和收敛速度全面提升,均优于PSO和GA。 表3 WOA最终配送方案 表4 GA算法最终配送方案 表5 PSO算法最终配送方案 续表5 图1 各算法收敛对比图 统计各算法50次求解的最终解(FS)、平均值(AS)、平均收敛代数(AD)和标准差(SD)等指标如表6所示。 表6 各算法求解结果对比 (单位:万元) 根据表6,IWOA的平均值和标准差最小,分别为8.52万元和2.36万元;GA次之,分别为13.43万元和6.24万元;WOA较大,分别为14.98万元和6.58万元;PSO最大,取值为15.27万元和6.75万元。由此可知,WOA稳定性优于PSO但弱于GA。经过本文改进,IWOA稳定性有效提升,依次优于GA、WOA和PSO算法。 为进一步验证IWOA的求解性能,分别利用IWOA、WOA、GA和PSO对VRP国际标准算例进行50次求解,统计求得最终解(FS)、平均值(AS)和平均运行时间(AT)如表7所示,IWOA求得最终配送方案如表8所示。 表7 各算法标准算例仿真结果 表8 IWOA最终配送方案 如表7所示,IWOA能够求得小规模算例A-n37-k5最优解,更新算例B-n31-k5最优解,且求得最终解与大规模算例A-n63-k10、B-n66-k9最优解相差仅为1.4%和1.1%,而GA、WOA和PSO不能求得任一算例最优解。IWOA平均运行时间最短,PSO和GA次之,而WOA运行最慢。同时,IWOA求得平均值最小,GA和WOA次之,而PSO求得平均值最大。 综上分析可知,WOA全局寻优能力和稳定性优于PSO、弱于GA,且收敛速度最慢。但经过本文改进后,IWOA在全局寻优能力、收敛速度和稳定性方面大幅度提升,明显优于WOA、GA和PSO。所以,虽然IWOA在参数设置难度上有所增加,但却能够大幅提高算法求解性能,进而大规模降低企业配送成本,这对于以利润最大化为追求的企业来说显然是值得的。 本文主要对长江经济带配送问题的求解算法进行了研究。针对标准WOA容易陷入局部最优解的问题,本文首先采用混沌机制生成WOA初始种群,然后先后引入自适应惯性权重、蛙跳算法和模拟退火算法对WOA进行改进,进而提出了求解长江经济带配送问题的IWOA。基于长江经济带配送实例和国际标准算例的仿真实验表明,改进后的IWOA求解性能优于标准WOA、GA和PSO,为长江经济带配送问题的求解提供了一种新思路。3.6 引入模拟退火算法
3.7 改进鲸鱼算法在长江经济带配送问题中的实现步骤
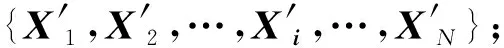

4 实例分析
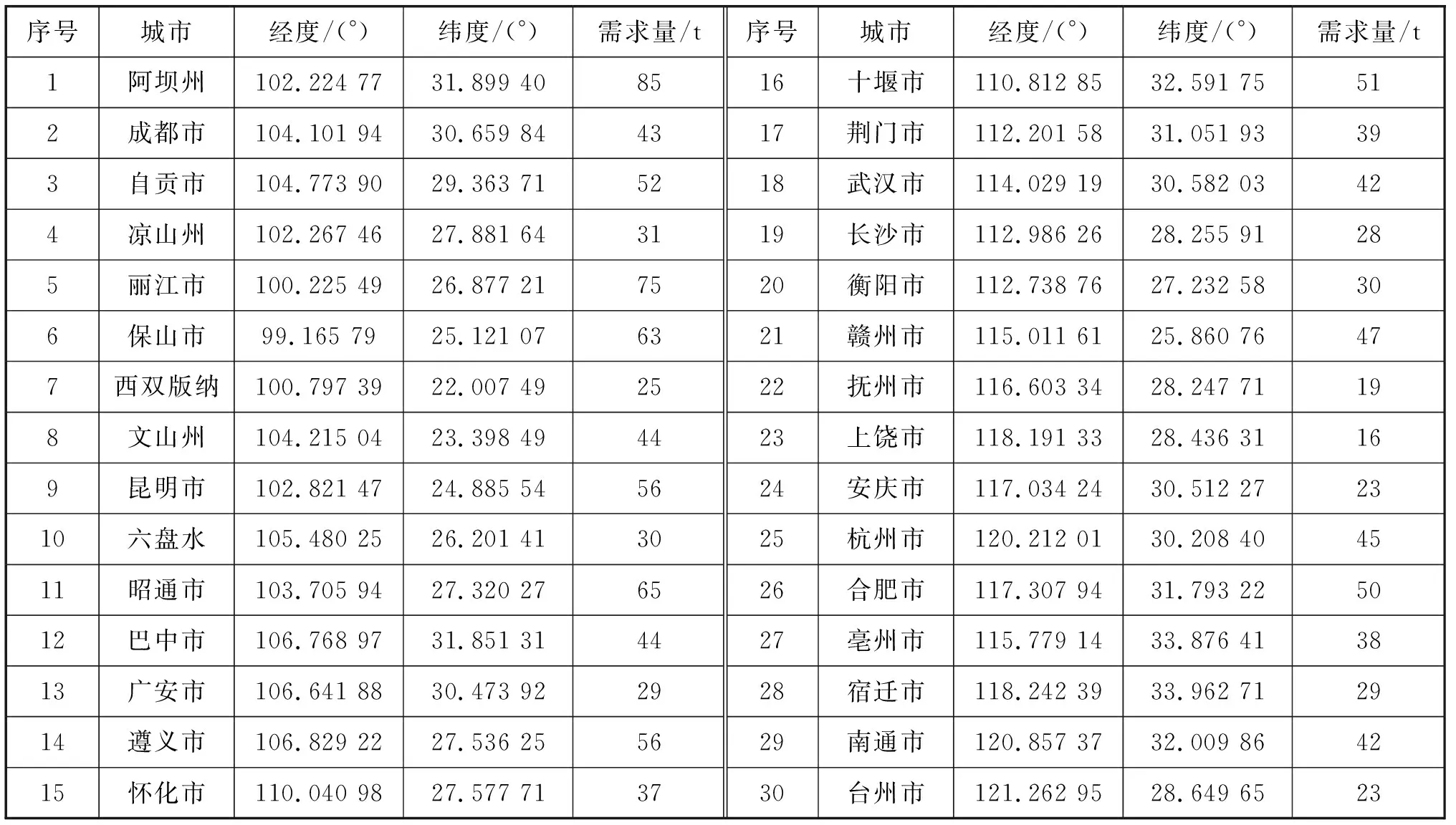
4.1 长江经济带企业配送实例

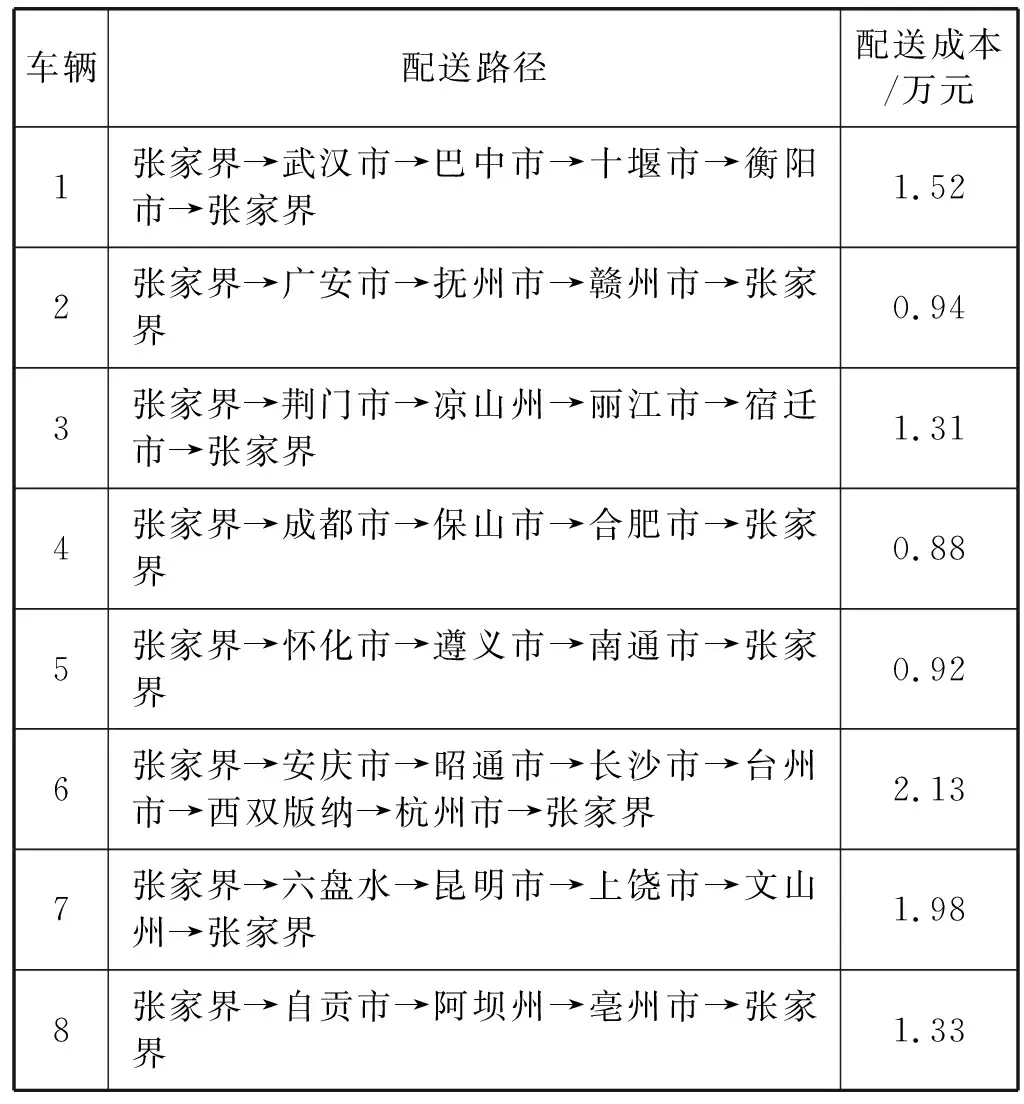
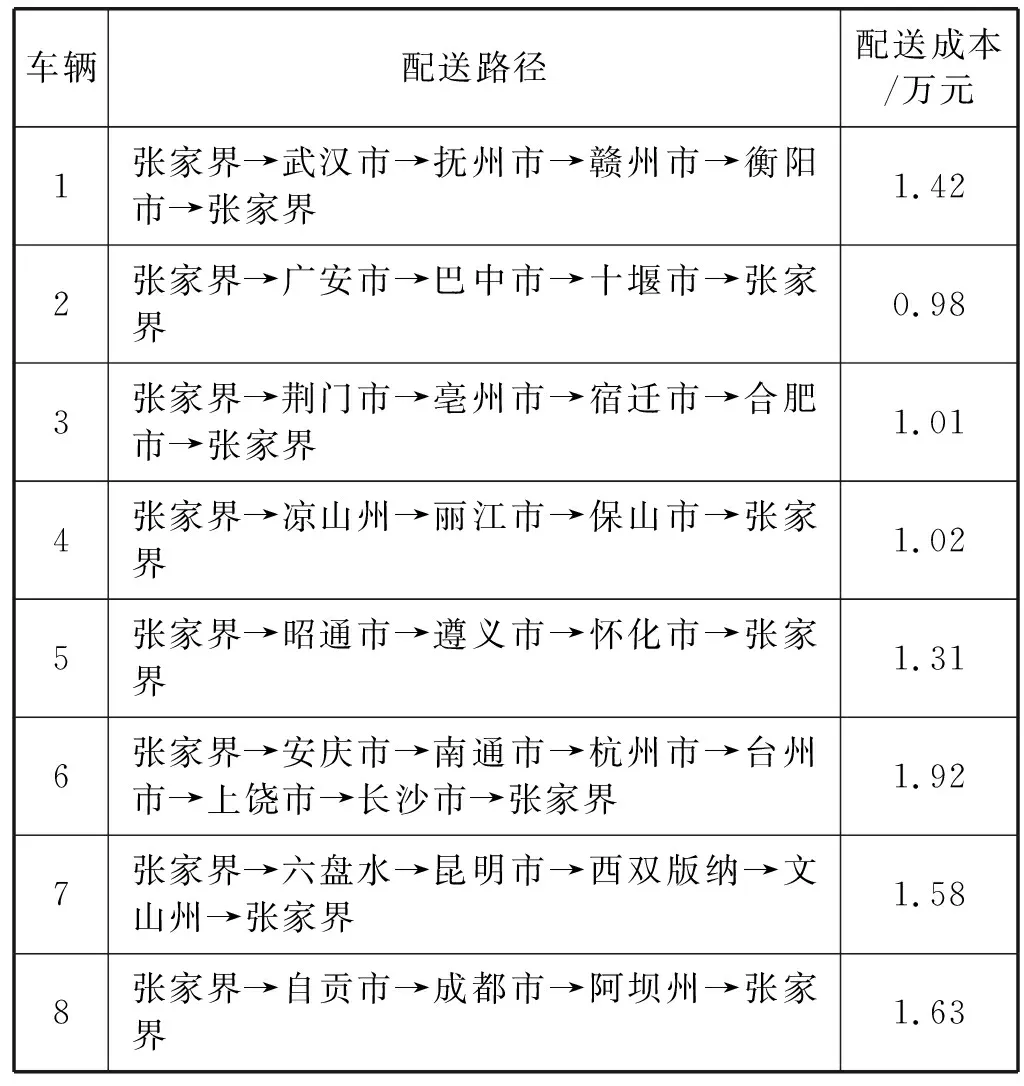

4.2 标准算例
5 结 语
