基于模方迭代算法的惯组参数辨识研究

李金钊 莫营 李渤通

（1.中国科学院长春光学精密机械与物理研究所 吉林省长春市 130000）

（2.国家计算机网络应急技术处理协调中心吉林分中心 吉林省长春市 130000）

1 引言

作为重要的导航方式之一的惯性导航系统，在飞机、舰船等载体上与其他系统无信息的交互，具有高可靠性、高自主性以及全天候运行等特点。惯导系统被应用的领域是非常广泛的，其发展前景也是备受瞩目。

在惯导系统的外场应用中，装载在飞机、舰船等运载体上的光纤捷联惯组系统，伴随着时间的推移与外部环境（温度、湿度）的变化，其内部结构也会随之发生变化，如陀螺光纤环光路的改变等原因，均会改变光纤陀螺误差模型的各组参数。同理，加速度计的误差模型参数也会发生改变。于是，光纤捷联惯组系统在工作一段时间后，应该对其内部的陀螺以及加速度计误差参数重新标定。

针对以上不足，在国内方面，王岩探索了沿X，Y,Z轴依次对光纤陀螺进行正转、反转操作辨识误差参数的方法以及经惯组系统沿三个轴向转动24个位置辨识出加速度计的各误差参数的方法。赵桂玲、卿立等人用经惯组系统转动6个位置的方式计算出惯组系统的各误差参数。康航宇提出了经惯组系统转动12个位置的方式计算出惯组系统的各误差参数，周章华提出了经惯组系统转动10个位置的方式计算出惯组系统的各误差参数。国外方面，Hung.J.C.等人探索了将惯组系统固定在十二个位置静态测试的实验，计算出加速度计各误差参数的方法，Mark.J.等人首先建立惯组系统的误差模型，然后研究了参数辨识中转台误差的影响，其着重记录了转台的稳定性数据以及指向性数据，证明了转台精度越高，惯组系统的误差参数计算精度越高。综上所述，国内外专家探索的惯组误差参数标定方法均为惯组系统在一段时间后从载体上分离出来，再利用转台等设备对其重新标定，这种方法不但会使设备的维护成本增加，而且会增加设备的损耗。为了完成惯组系统在实际工程中长时间使用的要求，研究无需高精度转台辨识惯组误差参数的算法成为必然。

探索在外场快速辨识惯组误差参数的方法已经成为当今热点问题之一。本文所探索的模方迭代参数辨识法是不同于以上利用高精度转台在实验室标定辨识参数的方法。其是基于在光纤捷联惯组在静态条件下，光纤捷联惯组的理想输入值依次为地球的自转角速度和重力加速度，并以陀螺和加速度计输入输出的模方相等为约束条件，来完成对于捷联惯组的判定，利用上述数据以及惯组器件的误差模型计算出各参数项、进而分析各参数精度指标。本方法对三轴转台的精度基本无要求，甚至可以在飞机、舰船载体上直接标定，这样就隔离了转台的误差对误差模型各参数的影响，这样就可以实现外场惯组误差参数的标定，具有较高的发展潜力。

2 参数辨识的误差模型

2.1 光纤陀螺误差模型的简化

因为光纤陀螺的线性度好的原因，所以在解算其误差参数时，选择以下4个参数作为误差模型的参量：

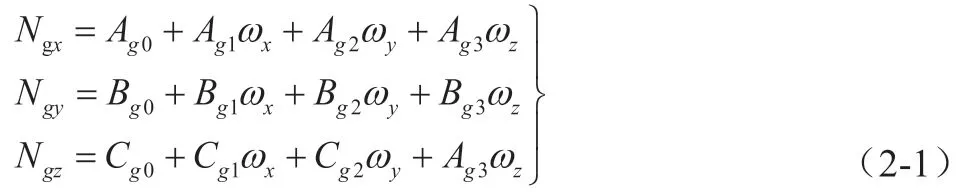
其中，N、N、N依次是惯组系统中x、y、z轴陀螺的输出值；A、B、C依次是惯组系统中三轴陀螺的零偏；A、B、C依次为三轴陀螺的刻度因数；A、A、B、B、C、C依次是三轴陀螺的安装误差和刻度因数的乘积，即A=KE。

因为模仿迭代法主要应用与外场惯组器件的标定实验，所以需要对其误差模型进行简化处理。

光纤陀螺作为惯组系统的主要元件有很多的优点，如其有反馈控制元件，当旋转角度变化的时候，由于干涉光波的作用，总可以保证相位不变，这就可以使其有好的线性值。上述优点，即简化了误差参数的辨识实验，又可以兼顾解算过程。因此，选取包含2个误差参数的数学模型，其形式简化如下：

把式（2-2）写成矩阵形式为：

其中：

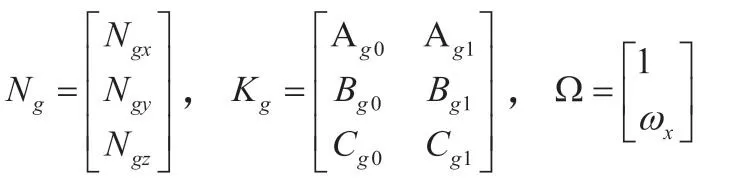
利用式（2-3）所表示的误差模型，即可以方便的表达出每个误差参数和光纤陀螺输入输出的关系，也可以在迭代求取误差参数的过程中减少计算量，使误差参数辨识的效率得到提高。

2.2 加速度计误差模型的简化

由理论推导可以发现，含有参数项多、阶次高可以使误差模型精确度更高，有利于对于误差的补偿，所以选择5个误差项。但在误差项增多后解算的工作量会很大，不利于效率的提高。因此，在实际工程应用中，会将二次耦合项去掉，得出加速度计的误差模型如下所示：

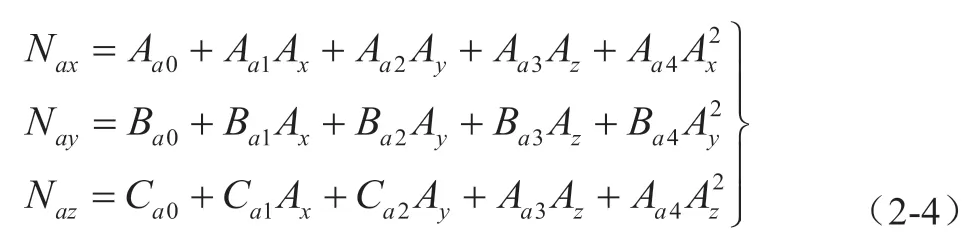
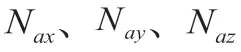
将式（2-4）转化为式（2-5）的形式，便于矩阵运算。

其中：

因为石英挠性加速度计具有的特性以及外场标定的实际状态，对上述加速度计的误差模型可以做更简洁的处理，如（2-5）式的加速度计静态误差模型去掉其它两轴以及耦合含有的误差项。这样，模方法辨识参数时的误差模型就构建出来了，如下所示。

把式（2-6）写成参数辨识中使计算变得简洁的形式为：

其中：

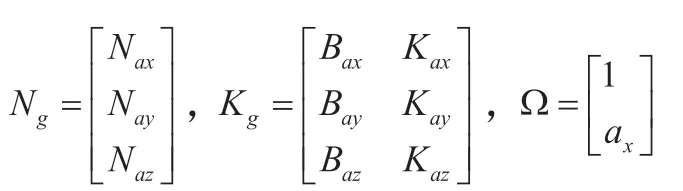
3 模方迭代法参数辨识

3.1 加速度计误差模型的简化

光纤捷联惯组系统的模方迭代参数辨识法，其具体判定方法是依据于当光纤捷联惯组在静态条件下，光纤捷联惯组的理想输入值依次为地球的自转角速度和重力加速度，并以陀螺和加速度计输入输出的模方相等为约束条件，来完成对于捷联惯组的判定。此方法为评估惯组标定精度的准确性提供了重要依据。

在静止状态下，惯性器件的输出向量满足以下方程：

根据式（3-1），对陀螺仪以及加表的实际测量输出值进行依次取模处理，得：

公式（3-2）和（3-3）表明，静止状态时，由于陀螺仪的输入激励为地球自转角速度而加表的输入激励为重力加速度由此可以看出其激励是确定的，与惯性测量单元的姿态无关，所以可以将陀螺和加表输出量的模作为判定量，可以计算出加速度计和陀螺误差模型的参数。

由（3-2）和（3-3）式以及惯性测量单元的输入输出模方相等的判据，在理想状态下，三轴陀螺以及加速度计的输出一定符合下式：

而从式（3-4）和（3-5）可以获得光纤陀螺以及加速度计的各轴输入值为：

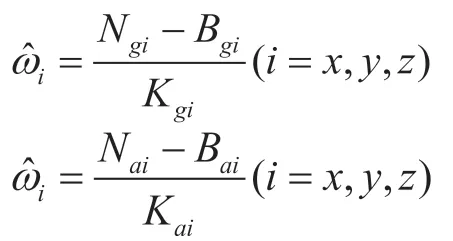
由于在实际量测时，会产生各种误差对系统造成影响，导致陀螺仪输入的实际计算值和地球自转角速率并不相等，因此列写如下的模方误差方程：

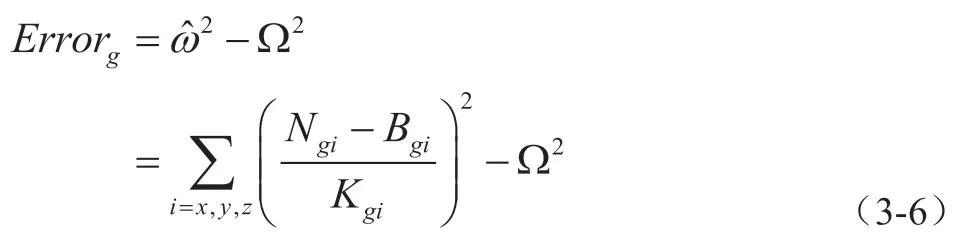
同理，列写加速度计的模方误差方程如下：

当模方误差最小时，其中零偏与刻度因数的值就可以达到最优，所以在其中可以引入迭代逼近系数，用以校正惯性器件的零偏和刻度因数，使得逼近后的模方误差值逐渐趋于零。

可以用式（3-8）和（3-9）分别代表惯性测量单元刻度因数与零偏迭代逼近的过程：

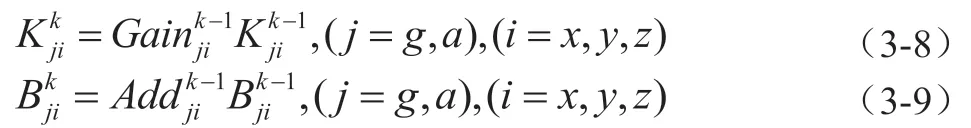
3.2 加速度计误差模型的简化

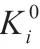
在进行次迭代逼近后，得到如下的形式：

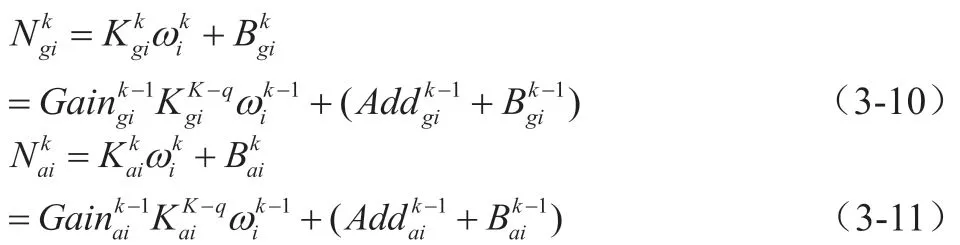
可根据上式推导出陀螺以及加速度计的迭代误差方程如下：

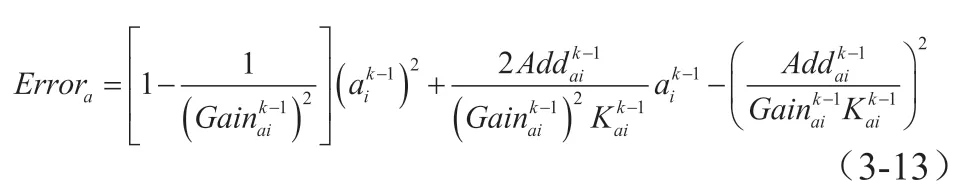
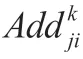
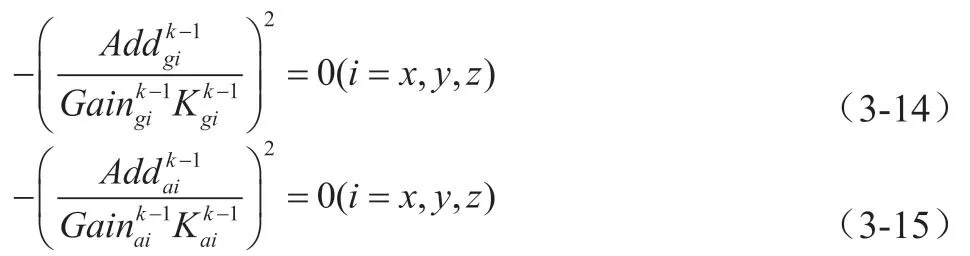
将式（3-14）和（3-1）分别代入式迭代误差方程中，可得：

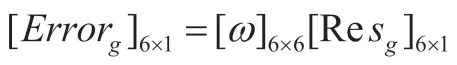
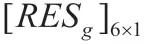
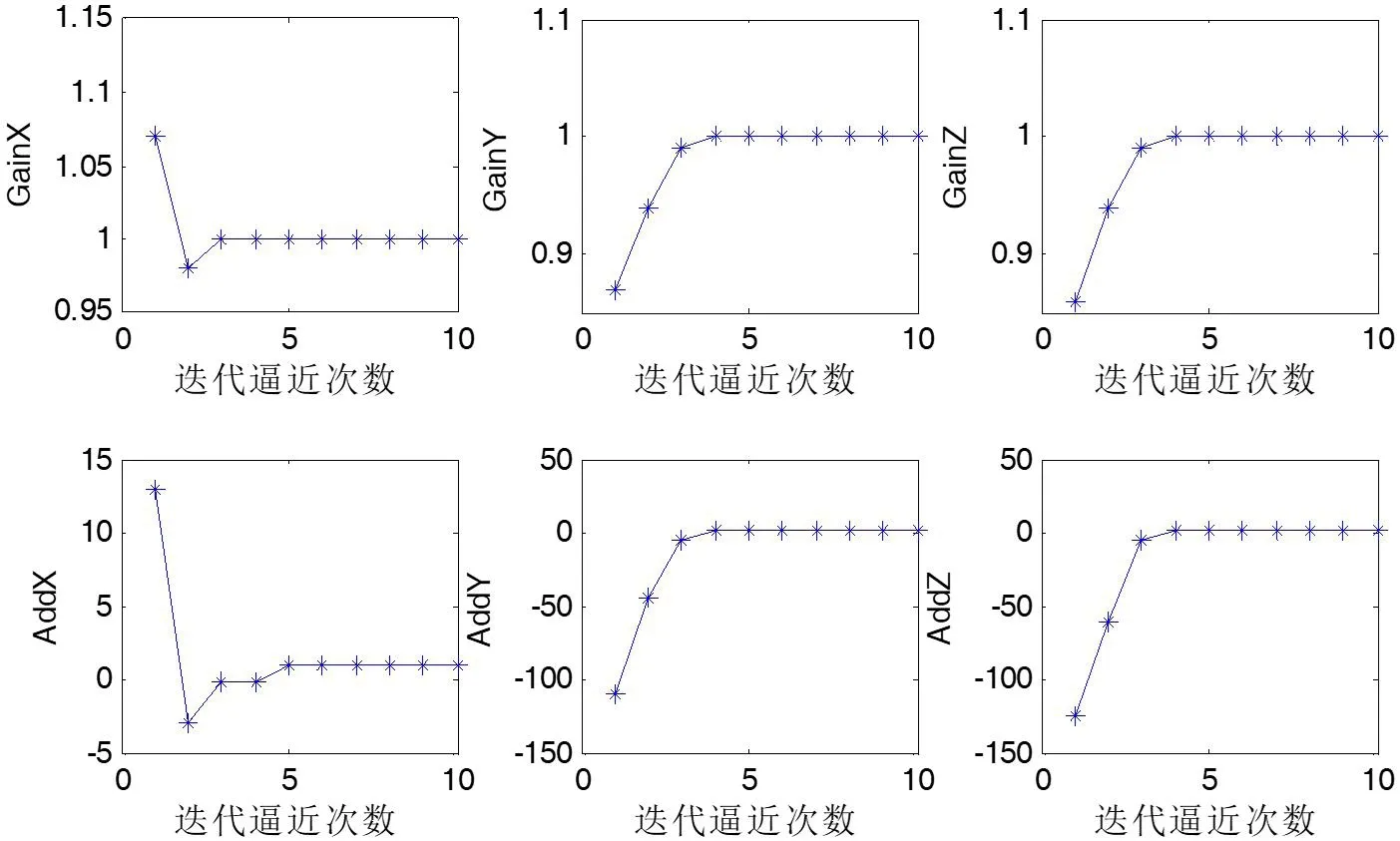
图7：陀螺仪迭代过程图7：陀螺仪迭代过程

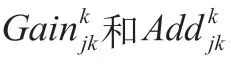
4 模方迭代法标定实验、仿真以及分析

4.1 速率/24位置法标定试验

本实验的参数辨识对象为如图1所示的惯组器件，测试转台为如图2所示的设备，其具有精度高、操作简便等特点。

图1：惯组设备

图2：SGT-3型三轴转台

利用图2所示的转台，利用24位置法与速率法依次对式(2-2)和式(2-6))中的误差参数进行辨识，对陀螺和加速度计的参数辨识实验方法如下所示。

以下为速率实验具体操作步骤：

（1）将固定在转台上的惯组系统的X轴与转台的中框重合，Y轴与转台的内框重合，Z轴与转台的外框重合；

（2）依据图3所示的陀螺位置，将陀螺的z、y、x轴依次指向天向。

图3：光纤陀螺位置实验初始编排

（3）以固定速度正向、逆向转动转台，记录转动n圈惯组系统的数据。（n为整数）

以下为24位置法实验具体操作步骤：

（1）将固定在转台上的惯组系统的X轴与转台的中框重合，Y轴与转台的内框重合，Z轴与转台的外框重合；

（2）以图4所示为惯组的初始位置，控制转台，将其X,Y,Z轴分别指向天向；

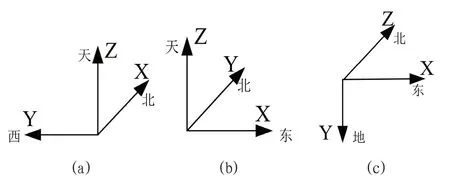
图4：位置实验惯组初始位置

（3）将上述的每组实验中的惯组系统沿北向轴旋转45°，转动7此后，形成24个位置，记录惯组的输出数据。

经速率实验以及24位置实验后，惯组系统的各项参数辨识结果如表1、表2所示。

表1：陀螺参数辨识结果

表2：加速度计参数辨识结果

4.2 模仿迭代算法的仿真及实验验证

当利用模方迭代逼近法辨识所有的误差参数时，应获得惯性测量单元6个位置的输出数据，其位置设计如图5所示，以及陀螺对应6个参数如表3，实验设备和控制上位机界面如图6所示。

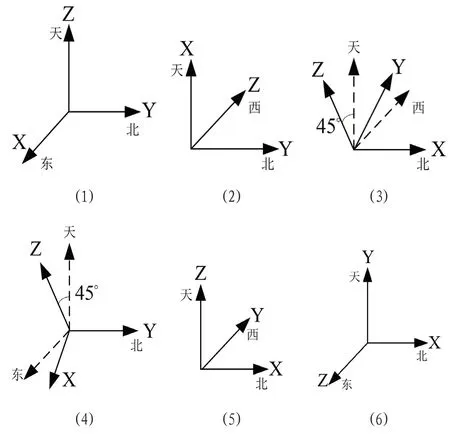
图5：位置编排

图6：实验设备和上位机界面

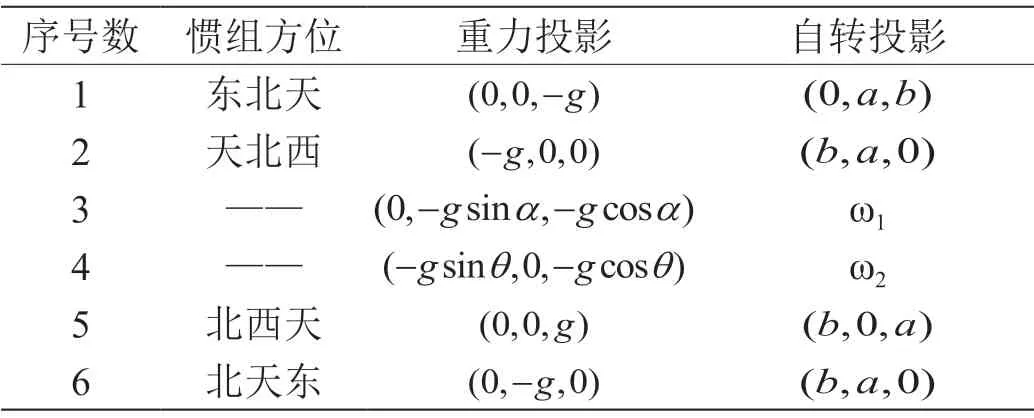
表3：实验参数设置

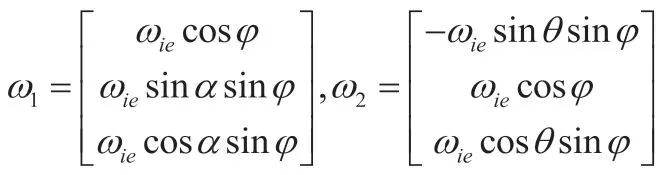
按照上述的陀螺与加速度计的简化模型和以传统标定方法的结果作为迭代初始值，陀螺与加速度计的三轴迭代过程如图中7和8所示。

图7：陀螺仪迭代过程图7：陀螺仪迭代过程

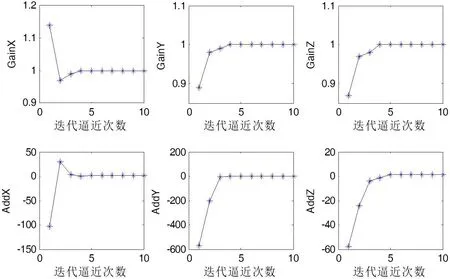
图8：加速度计迭代过程

从以上两图可看出，陀螺的各项参数在迭代逼近7次后达到理想值，加速度计的各项参数在迭代逼近4次后就达到了最优值，这表明使用模方迭代法时，加速度计的迭代效率要比陀螺的效率高。

得到的标定结果如表4所示。

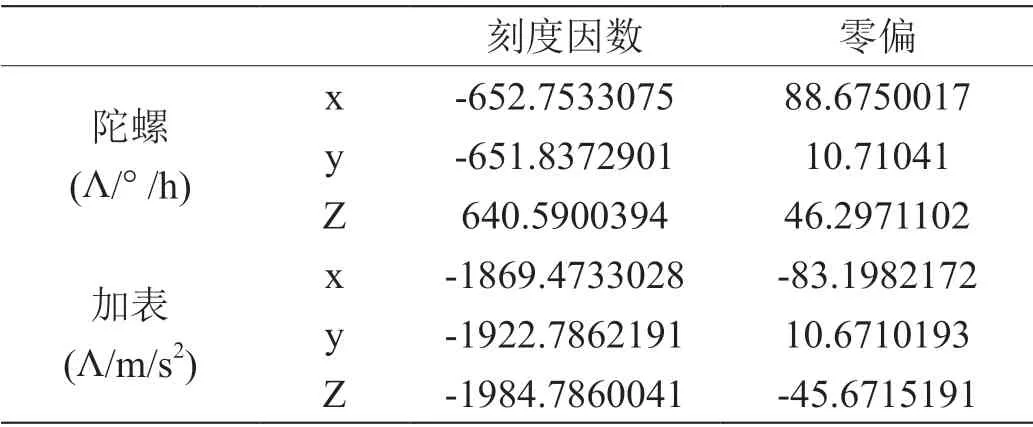
表4：模方法参数辨识结果

由表4分析可知，基于出场误差参数，可利用模方迭代法快速辨识惯组系统的各误差参数。对比表4以及表1、表2可知，在参数辨识过程中，模方迭代参数辨识法与传统标定方法精度大致相同。但模方迭代法可以脱离转台在实际工程现场通过翻转惯组的位置即可以实现标定。由实验可知，本方法即可以保证精度，又可以使标定时间、标定成本明显降低，有更好的实际使用价值。

5 结论

由于工程现场惯组器件标定的重要性，本文使用模方迭代算法对惯组器件的参数进行辨识，首先建立惯组器件(陀螺、加速度计)误差的简化模型，以便外场能更高效的辨识惯性系统的参数；然后利用模方迭代算法的原理推导标定公式，其本质上就是参数修正“迭代”的过程，当参数为常值时，此时的结果就是标定的最优解。最后，利用逐次逼近迭代的方法对模方法进行验证，说明这种方法在野外具有较高的应用价值。