填充床熔盐蓄热器的动态温度与应力特性

聚光型太阳能热发电(concentrating solar power，CSP)技术是利用太阳能的有效方式之一，近年来得到了非常广泛的应用

。然而，由于昼夜循环和云层遮挡引起太阳能资源时空间歇性不稳定，使得热发电站发电和用电周期具有不匹配的运行特性，因此CSP 系统急需解决蓄热问题，以提高系统运行的稳定性，从而更灵活地满足发电的需求

。目前，已商业化运行的电站均采用双罐熔盐蓄热系统，其中熔盐既充当换热流体又充当蓄热介质，成本比较高。采用单罐熔盐填充床蓄热系统不仅可以利用廉价易获取的固体材料代替昂贵的熔盐作为蓄热工质，而且结构简单，与传统双罐蓄热系统相比可降低30%的投资成本

。然而，填充床蓄热器在运行的过程中仍会面临如下问题：①蓄-放热过程中，由于罐体内外壁面存在温度梯度，造成罐壁应力损伤，经过多个蓄-放热循环周期后，动态应力损伤累积致使蓄热器壁面产生低周(应力幅高于屈服强度)或者高周(应力幅低于屈服强度)疲劳断裂失效现象，严重影响蓄热器的使用寿命；例如，美国Crescent Dunes、西班牙GemaSolar 与摩洛哥NOOR III 塔式熔盐电站的蓄热罐体就产生了应力导致的熔盐漏露事故，并造成了较大经济损失；②在长周期的蓄-放热循环中，若壁面温度高于材料的蠕变温度阈值，罐体还会进一步产生缓慢塑性变形的高温蠕变现象，增加蓄热器的失效风险；③在疲劳与蠕变的交互作用下，填充床蓄热罐体的断裂失效速率加快，从而给CSP 系统的安全运行带来极大挑战。

近年来国内外研究人员针对填充床蓄热器已开展了大量的研究工作。在流动换热方面，Pacheco等

对蓄热量为2.3 MWht的单罐蓄热器进行了理论分析和实验研究，结果表明了单罐熔盐填充床蓄热系统的可行性。尹辉斌等

建立了单罐斜温层系统的二维数值模型，研究了多孔填充床内斜温层的蓄放热过程。结果表明斜温层的存在会降低系统的蓄热效率。Xu 等

建立二维、瞬态、非热平衡模型，探讨了运行与结构参数对填充床熔盐蓄热器放热性能的影响。为了提高填充床蓄热器的蓄热效率，Li等

提出了一种三层的填充床蓄热结构(石英岩-铸铁-高温混凝土)以提高系统的有效蓄热量。同时，Zhao 等

数值分析了填充床构型(相变-显热-相变)对蓄热性能的影响情况，并给出了成本最优的填充结构样式。

应力特性研究方面，Flueckiger 等

首先建立单罐蓄热系统的非热平衡模型，在此基础上获得了蓄热器热性能，接着采用静力学应力-应变模型研究了罐壁和保温层厚度对应力的影响情况。同时，Wang 等

也探讨了不同参数对填充床蓄热器应力特性的影响。结果表明，采用低孔隙率、小直径、低导热系数的填充材料有助于降低壁面的应力水平。另外，张晓明等

同样利用有限容积法对高温熔盐储罐的热性能进行了模拟研究，并对其进行了静力学分析，结果显示罐体最大应力位于大角焊缝内侧底部区域。Wan等

利用有限容积法模拟得到双罐蓄热系统中高温熔盐储罐在不同蓄热水平下的热损失与罐壁的温度分布，接着采用有限元方法探讨了储罐在不同条件下的力学性能。

综上可知，由于蓄-放热循环下壁面温度与应力的动态变化规律是影响填充床蓄热器在寿命期内是否产生应力疲劳与高温蠕变的关键因素，而目前针对填充床蓄热器应力特性的研究主要集中在采用有限容积法和有限元法讨论不同运行与结构参数对罐体应力特性的研究方面，同时，经历多个蓄-放热循环下壁面动态温度与应力变化的研究也鲜有报道。因此，本文利用有容积法与有限元法建立了填充床蓄热器的热-力耦合数值模型，模拟研究了多次蓄-放热循环工况下蓄热罐体的温度与应力的动态变化规律，并获得了蓄热器产生塑性屈服与高温蠕变的失效区域。本文的工作可为接下来开展单罐填充床蓄热器的寿命预测研究提供有效的参考依据。

1 物理模型和数值模型

1.1 物理模型

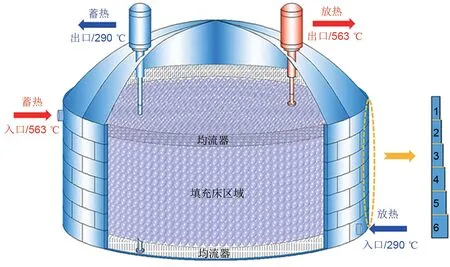
本文选用塔式熔盐CSP 电站中的高温熔盐储罐作为所建立模型的参考依据，罐体内径(

)为25 m，高度(

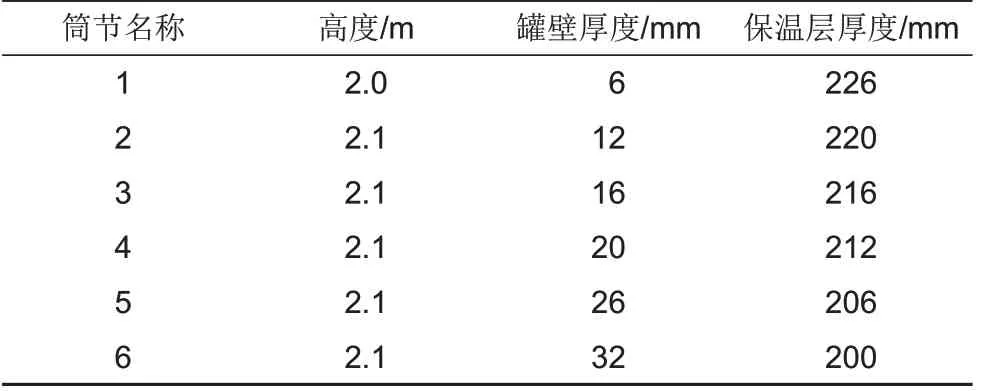
)为12.5 m，特别地，罐体壁面由逐级增厚的阶梯状变截面壁板组成

，共分为6 段筒节，具体结构如图1所示。其中，壁面与保温层的厚度以及每层筒节的高度如表1所示。此外，填充床区域由球形固体颗粒组成，颗粒直径(

)为19.05 mm，孔隙率(

)为0.22。

1.2 材料特性

用应力表示的变形协调方程：

1.3 控制方程

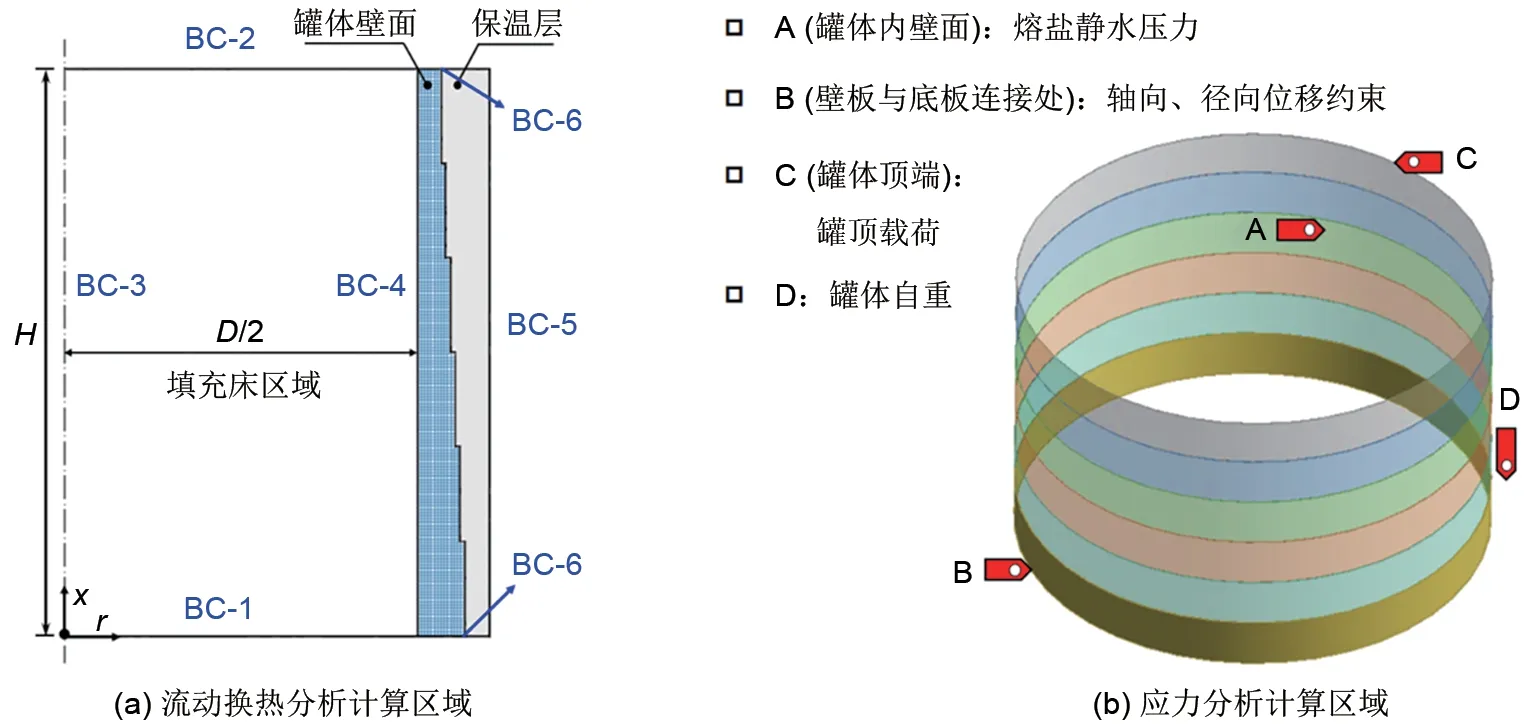
针对以上物理模型，建立了二维、瞬态、轴对称的多孔介质非热平衡数值模型，为简化计算，选用图2(a)所示的填充床区域为计算区域，并作以下假设：①计算区域入口和出口流速均匀分布；②流体在填充床区域为不可压的层流状态；③固体填料为连续、均质的多孔介质；④固体填料为等直径的球状颗粒。

此外，为了精确得到罐体壁面的动态应力变化规律，根据表1给出的罐体结构参数建立了图2(b)所示的三维数值模型。特别地，由于保温层只起到减少热损失的作用，不参与结构承载，因此在进行应力分析时未考虑保温层对结构力学特性的影响。

大数据可以控制教学进度，指导教师掌握教学中的侧重点，提高学生的学习能力，在大数据的影响下教师可以最大程度地发掘出学生们的学习潜力，从而提高学生们的学习成绩。可以根据大数据对教学制度、教学结构进行分析。对学术进行分析，让资源合理分配。最重要的是对学习者进行分析，充分了解学习者学习情况。

针对上述假设，建立了如下的控制方程。

运用映照的修辞修辞格，将年幼时的“我们”与现在经历事件而走向不同的“我们”进行对照，展现岁月终使“我们”走向分离的残酷。

罐体自身结构和安装方式决定了应力分析的边界条件，如图2(b)所示。由于罐体壁板与底板采用槽钢进行焊接固定，使得壁板底端无法在径向与轴向上收缩变形，因此应力分析时设置了位移约束。值得注意的是，熔盐液位对内壁面引起的侧向水压力，可视为孔隙水静压施加在罐体内壁面上，其中，静水压力可由公式(23)与(24)计算获得

。此外，罐体壁板顶端施加拱顶载荷，同时，应力分析模型中也考虑了罐体的自重荷载。

1.3.1 流动换热分析控制方程

熔盐连续性方程：

式中，

为蓄热罐中填充床的孔隙率；

为固体颗粒的直径，m；下标f 代表熔盐；

与

分别为多孔介质的黏性阻力系数与惯性阻力系数。

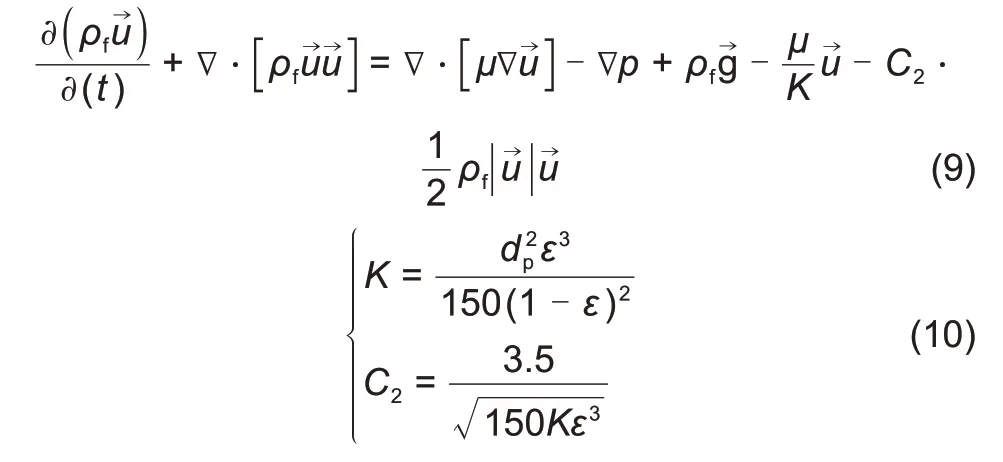
熔盐动量方程：

罐体壁面和保温层的能量方程：

信息化是内部控制的重要手段和落地方式，通过建立绩效管理系统实现预算绩效管理信息化覆盖，加强采集预算绩效信息的工作，定期监控与跟踪预算绩效信息，确保能够及时反映预算绩效管理情况。各预算单位要增强财务处理与信息处理能力，信息技术的应用也可以极大地减少人为干预，更有力地落实职责分离要求，为预算绩效监督提供更加真实可靠的信息平台，使监督反馈的结果更加准确和符合单位实情。

熔盐能量方程：

固体填料能量方程：

染料木素甲氧基封端的聚乙二醇-乳酸羟基乙酸共聚物胶束在小鼠体内的组织分布研究 ………………… 何 礼等（11）：1496

式中，下标s与eff分别表示填料与有效值，

表示蓄热器中填料与熔盐之间的对流换热系数，W/(m

·K)；

和

分别为熔盐和填料的有效导热系数，W/(m·K)。

伴随着课程改革的逐步推进，自主、合作、探究的学习模式已经成为大势所趋，并成为教师们教育教学中的要点所在。而借助于小组合作这一模式的引入，就可以帮助教师达成这一目标，以进一步地推动学生的发展，使其深切地感受到知识形成的整个过程，这对于课程改革的推进，将有着非常重大的意义。

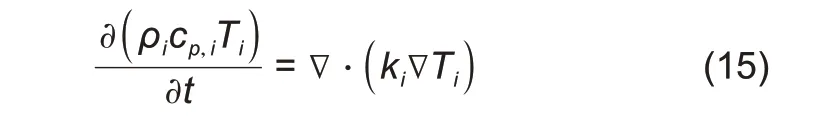
下标

表示罐体壁面和保温层。

1.3.2 应力分析控制方程

在蓄-放热循环中，由于罐体壁面既受到由温度梯度导致的热应力影响，也受熔盐流体静水压力的作用，因此，应力、应变与位移等参数可基于热弹性力学方法进行求解。基于热弹性力学理论，变温条件下应力分析模型的控制方程主要包括：①反映应力与应变关系的物理方程；②反映应力与体力关系的平衡(运动)微分方程；③反映应变分量之间关系的应力协调方程

。

二○一八年二月十四日，我，把自己活成了当初你喜欢的模样。但是亲爱的，这是你现在想要的模样吗？是不是活成一朵花的模样，就很美好——不再遗失的美好？

4.对配电装置进行设计时以及对电器以及导体的最大风速进行选择时，一般采用离地10m高，在对屋外的配电装置进行布置时，一般应降低电气设备的安装高度，还应该对基础以及设备的固定进行加强。

用应力表示应变的物理方程：

用位移表示的平衡微分方程：

政府择优确定合作保险公司，在合作期间，政府为农户向保险公司缴纳政策性保险，以调动保险公司积极性，保险公司为借款人办理还款保证保险。当单笔贷款发生损失时，由县担保中心、银行和保险公司按1∶1∶8比例共同承担损失，偿付贷款本息。其中，政府承担风险上限为资金池内总额，银行承担风险上限为年度全部小额贷款总额的3%，保险公司赔偿上限为年度全部小额贷款保证保险保费总额的120%和农业政策性保险三年累计保费总额的70%与已实际赔付金额的差额部分。

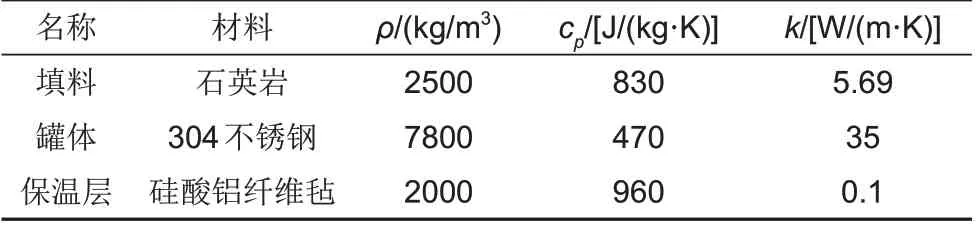
传热流体采用二元熔盐[60%(质量分数，余同)NaNO

和40% KNO

的混合物]，按变物性考虑

，具体物性见公式(1)～(4)。固体填充材料、罐体和保温层的物性参数如表2所示

，其中，罐体选用304不锈钢材质，线性膨胀系数

(K

)、弹性模量

(Pa)与屈服强度

(Pa)等力学性能见公式(5)～(7)

。

其 中，

=

(

/

)

+ 0.5

；m = 0.28 - 0.757log

- 0.057log(

/

)

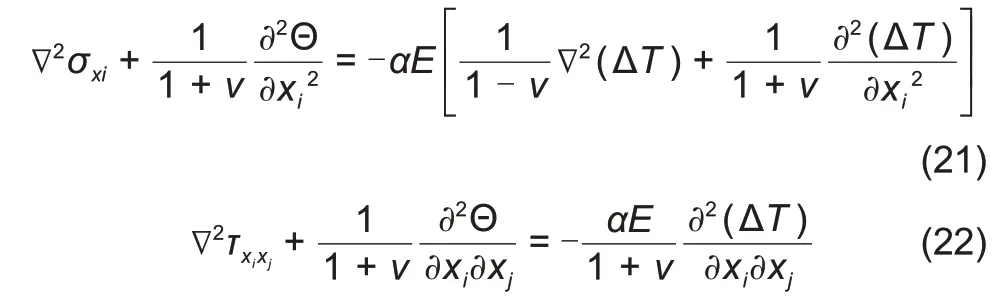
式中，

为剪切弹性模量，Pa；Δ

为内外壁面的温度梯度，K；

为体积应力，Pa；

为体积应变；

为拉梅常数。

1.4 边界条件

1.4.1 流动换热分析边界条件

对填充床蓄热器进行流动换热模拟分析时，边界条件包括入口边界(BC-1)、出口边界(BC-2)、轴对称边界(BC-3)、内壁面边界(BC-4)、外壁面边界(BC-5)和进出口壁面截面边界(BC-6)，如图2(a)所示，具体定义见表3。特别地，在CSP系统的实际运行过程中，为避免熔盐流体在较低罐体温度下凝固，蓄热罐体在投运前需预热至较高温度(573 K左右)，因此本文模拟时罐体的初始温度设为573 K。

1.4.2 应力分析边界条件

构建和谐企业的主要内容有三个方面：一是企业内部的和谐；二是企业与外部利益相关者的和谐；三是企业与外部环境的和谐。

知识点的教学过程设计是课程设计的基础和关键性工作。对于知识点的教学设计大致分为以下几步：首先，确定知识点名称及其在知识框架中的位置，明确知识点所需要达到的目的与要求。其次，思考如何对知识点进行导入，设计多少个PPT页面对知识点进行不同层次的分析与展示，每个页面内容所需要讲解的要点。最后，从知识点介绍与导入、分析与阐述、巩固与提升等方面，对在线视频内容进行详细设计，实现SPOC课程视频的脚本设计[6]。

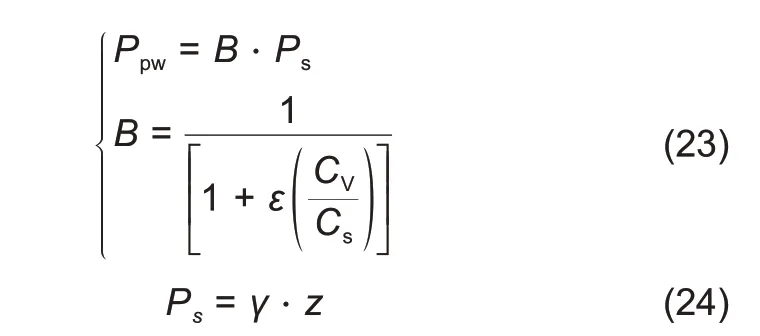
式中，

为孔隙水压力系数；

为液体压缩系数；

为骨架压缩系数；

为液体静水压力，Pa；

为液体容重，N·m

；

为液体深度，m。

2 数值方法和模型验证

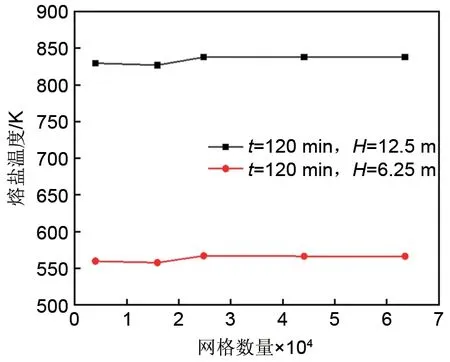
采用有限容积法对流动换热控制方程进行数值求解时，压力-速度耦合方程运用SIMPLEC算法求解，动量方程和能量方程均采用二阶迎风格式进行求解。对时间步长的独立性考核后，本文采用5 s的时间步长进行非稳态迭代计算。最后，对模型所划分网格的独立性进行了考核，图3给出了出口与中线位置(

=7 m、14 m)的熔盐温度变化情况。结果显示，当网格数量为24804时可获得独立解。为了验证本文建立的流动换热模型的可靠性，将模拟结果与文献实验值

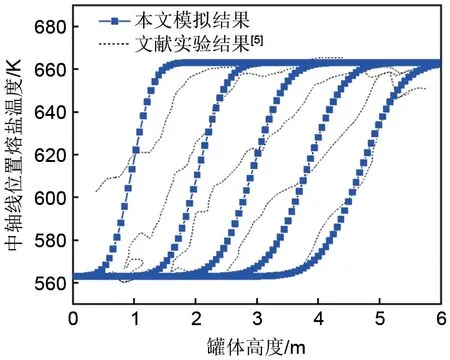
进行了比较，如图4 所示。可以看出，模拟结果与实验结果有很好的一致性，表明本文的数值模型是可靠的。

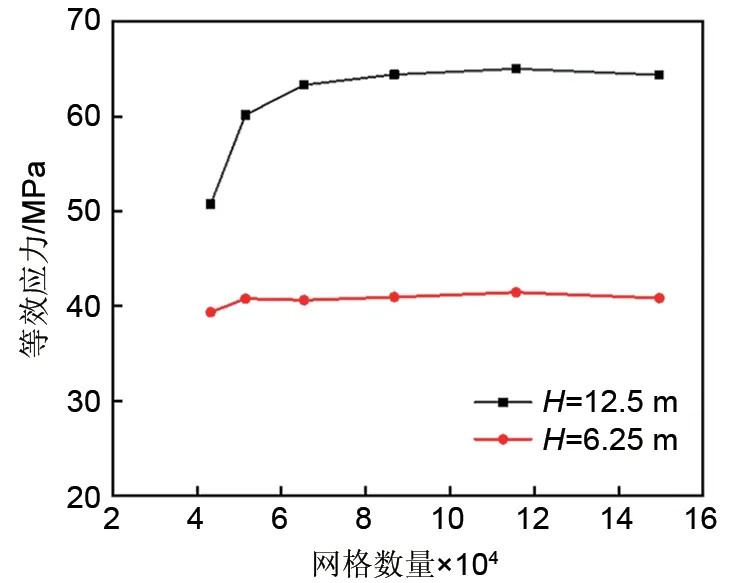
运用ANSYS 有限元软件进行应力分析时，对时间步长的无关性进行了考核，采用5 s 的时间步长进行模拟计算。同时，本文共建立了6套(3200、51480、65400、86760、115680、149640)网格模型。图5 给出了内壁面2 个高度位置处(

=6.25 m、12.5 m)的等效应力变化情况。结果表明，当网格数达到65400时，等效应力的变化幅度小于5%，考虑到计算量和计算精度，本文选用网格数为65400进行应力计算。此外，由于目前针对填充床蓄热器应力分析的实验研究工作还鲜有报道，因此，本文未对应力分析模型的可靠性进行验证。

3 结果与讨论

在CSP 系统中，由于蓄热器的动态应力特性是决定蓄热系统使用寿命的关键因素，因此，为探究蓄热器在高温蓄-放热循环过程中能否安全稳定运行，本文采用热-力耦合方法模拟研究了填充床蓄热器在连续蓄-放热循环过程中的温度与应力的动态变化特性。具体步骤为：首先，建立蓄热器的二维、轴对称、瞬态、非热平衡传热模型，并采用有限容积法模拟获得不同蓄-放热循环下罐体壁面的温度分布规律。接着，利用节点插值方法将二维温度场映射到三维罐体壁面应力分析模型中。最后，将不同蓄-放热循环次数下的动态温度分布作为接下来进行应力分析的温度荷载，然后利用有限元法模拟研究罐体壁面的动态应力分布特性。

3.1 单次蓄-放热循环

3.1.1 温度分布特性

取25 g经国标法检测无沙门氏菌的肉制品加入到225 mL的无菌生理盐水中，制成匀浆液，取9 mL加到离心管（10 mL） 中，分别将10倍梯度稀释的菌悬液（5.1×107～5.1×102CFU/mL） 各1 mL加到上述离心管中，混匀，得到不同浓度的菌液匀浆。用1.2.2中所述热裂解法提取基因组DNA，并用RF-LAMP方法验证人工污染肉制品中沙门氏菌的检出限。

图6给出了第1次蓄-放热循环不同时刻下罐体壁面的温度分布云图。可以发现，蓄热时高温熔盐流入、放热时低温熔盐流入的运行方式导致罐壁温度在蓄-放热过程中呈相反的变化趋势。同时，从图6(a)可以看到，由于在蓄热过程中罐体壁面与高温熔盐流体(838 K)换热，且通过导热方式吸收高温固体颗粒的热量，使得壁面温度逐渐升高，在蓄热结束时刻壁面整体温度达到最高。此外，由图6(b)可知，由于放热初始时罐体内固体颗粒温度较高(838 K)，且冷熔盐(563 K)会吸收壁面与填料的热量，使得罐壁温度又逐渐降低，在放热结束时刻壁面整体温度达到最低。

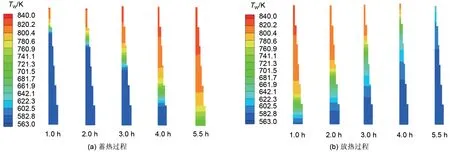
特别地，由于本文模型中304ss罐体材料的蠕变温度为783 K

，因此从图中也可发现，在蓄热过程中罐体壁面的蠕变区域逐渐增多，在放热过程中产生蠕变的筒节数量逐渐减少。

为了更加清晰地了解在蓄-放热过程下罐体壁面的高温蠕变情况，图7 进一步给出了不同蓄-放热时刻下沿罐体高度方向的壁面温度变化情况。从图7(a)可以看到，蓄热1.0 h 时，随着高温熔盐进入罐体，致使筒节1的壁面整体温度高于材料蠕变的温度阈值。蓄热结束时刻(5.5 h)，筒节1～5 的壁面均产生了高温致使的蠕变现象，造成壁面损伤。同时，由图7(b)给出的放热过程下的壁面温度分布可知，罐壁温度经历5.0 h 后均会低于材料的蠕变阈值。

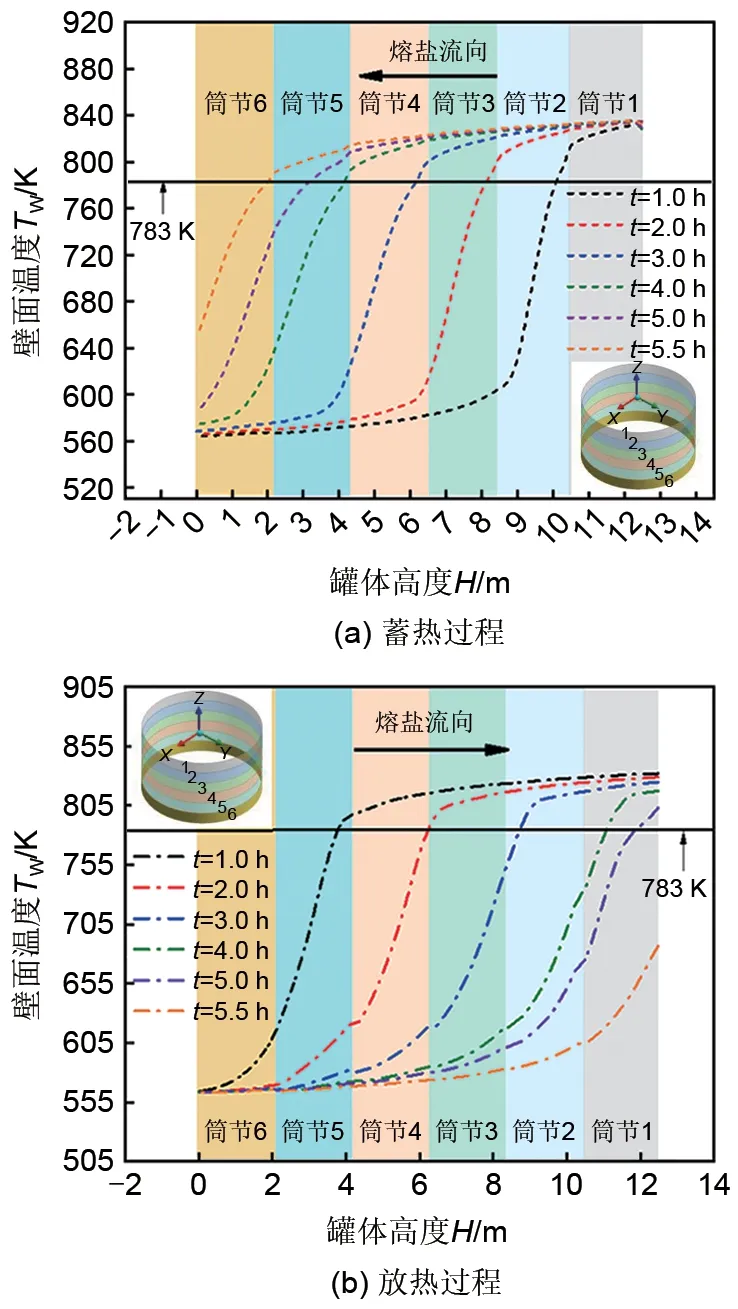
综合图6、图7可知，在蓄-放热过程，罐体壁面的大部分区域都会产生高温致使的蠕变现象。例如：蓄热时，筒节1～5 的壁面均会产生蠕变；由于放热初始与蓄热结束时刻的壁面温度相同，因此在经历5.0 h的放热过程中，筒节1～5的壁面也会产生蠕变损伤。此外，填充床的运行方式使得壁面的最高与最低温度分别出现在罐壁板顶端与底端的位置。

图8 给出了蓄-放热过程中罐体壁面最高温度随着时间的变化趋势。从图中可以看出，对于单次蓄-放热循环而言，壁面温度呈4 个阶段的变化趋势：蓄热时，高温熔盐从顶部流经均流器后进入填充床区域，由于内壁面吸收高温熔盐与固体填料的热量，致使壁面温度先急剧上升至最高温度(阶段Ⅰ)，然后保持不变(阶段Ⅱ)；放热时，冷熔盐从罐底进入填充床，斜温层逐渐向罐顶移动，使得壁面温度缓慢下降(阶段Ⅲ)，当斜温层快到达罐顶时，致使壁温又呈急剧下降的变化趋势(阶段Ⅳ)。

3.1.2 应力分布特性

为进一步了解在连续蓄-放热循环过程中罐体的动态温度变化对其应力特性的影响，本文接下来又通过热-力耦合方法模拟获得了不同蓄-放热循环下罐壁的应力分布情况。图9给出了第1次蓄-放热循环在不同时刻下的罐体壁面应力分布云图。从图中可以看出，在蓄-放热过程中，罐体顶端的应力值最小，最大应力出现在罐体底端区域。这是由于罐体壁面与底板连接位置处的结构形状急剧变化，且在该区域存在刚性约束(径向与轴向约束)，致使该连接位置的应力值最大，进而造成应力集中现象。

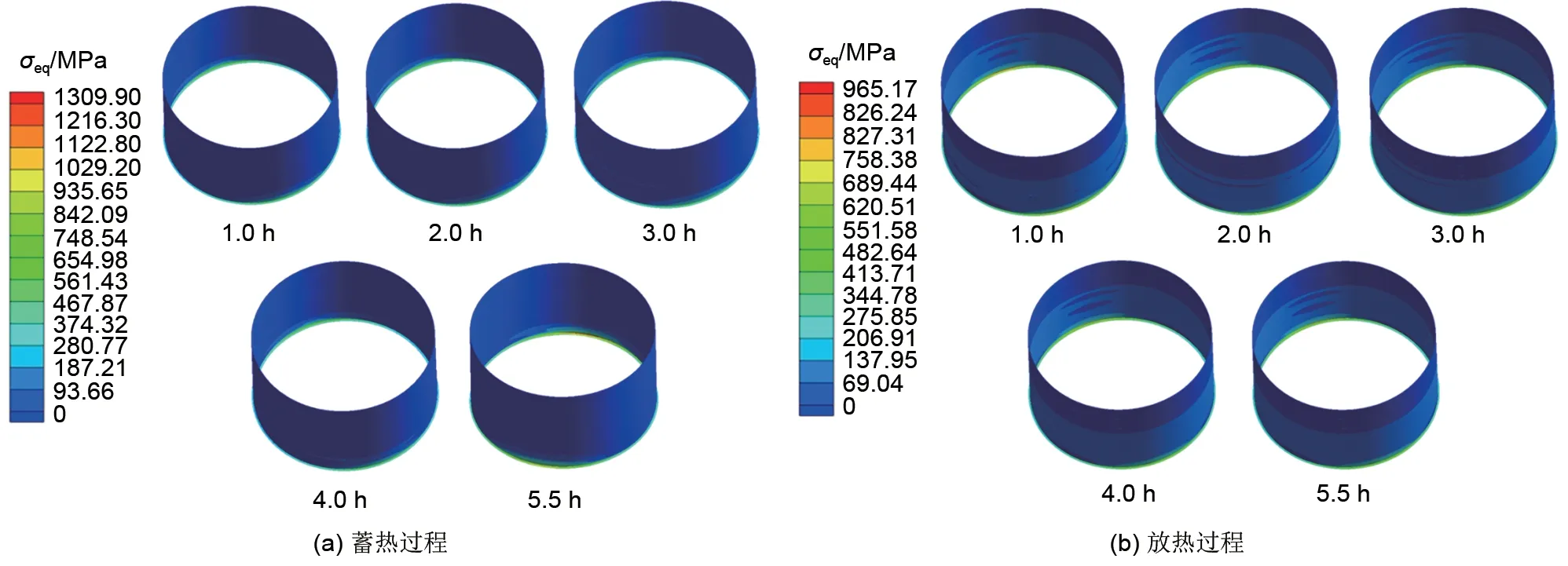
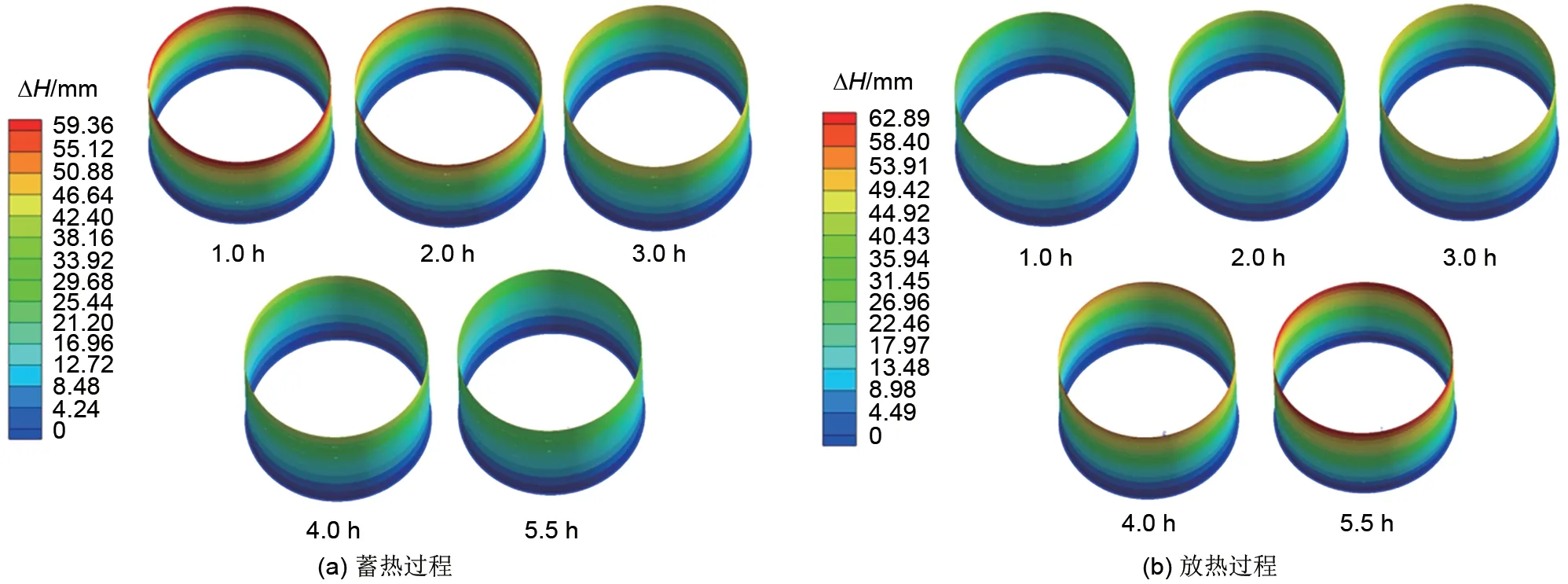
图10 给出了第1 次蓄-放热循环不同时刻的罐体形变分布云图。结合图6可知，罐体形变受温度影响显著，较高的壁面温度会产生较大的热变形。在蓄热初始与放热结束时刻，罐体的形变量最大，约为60 mm。

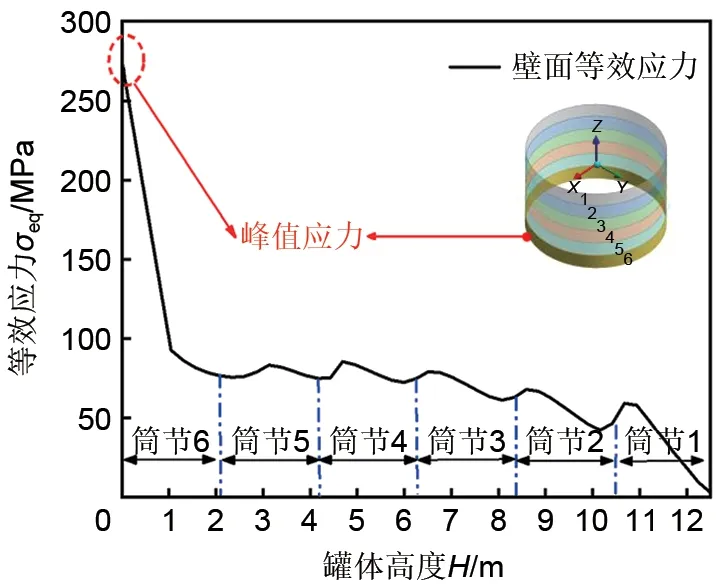
为了更加清晰地认识罐体应力的分布规律，图11进一步给出了第1次循环结束时刻沿罐壁高度方向的应力变化情况。可以看出，由于罐底为刚性约束，热膨胀量无法释放，致使第6筒节与底板连接处存在应力集中导致的塑性屈服现象；随着高度的增加，罐体应力水平逐渐降低，致使第1～5 筒节的壁面仍处于低应力水平(低于90 MPa)的弹性状态。

3.2 多次蓄-放热循环

3.2.1 温度变化特性

①通过肺炎双球菌体外细胞培养实验的结果，发现：在体外连续培养多代的S型菌和R型菌，各亚型S型菌均可突变为相应亚型R型菌（S-Ⅰ突变为R-Ⅰ；S-Ⅱ突变为R-Ⅱ）。综合观察现象和实验一结果，得出结论：R型菌是由S型菌突变产生的，且突变仅发生在同亚型间。

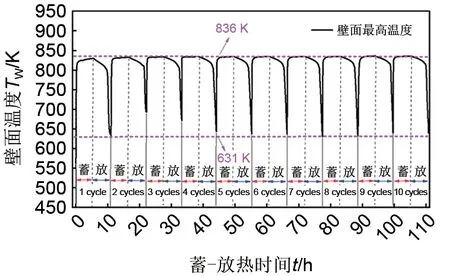
图12 给出了填充床蓄热器经历10 次蓄-放热循环(蓄-放热总时间1100 h)壁面最高温度的变化规律，从图中可以看出，随着循环次数的增加，壁面温度在631˜836 K 呈周期性变化趋势。特别地，结合图7与图11可知，填充床蓄热罐的大部分筒节也会产生周期性的蠕变现象，且随着蓄-放热循环次数的增加，低应力水平的壁面(筒节1～5)还可能会产生高温蠕变导致的断裂现象，从而增加填充床蓄热器的失效风险。

3.2.2 应力变化特性

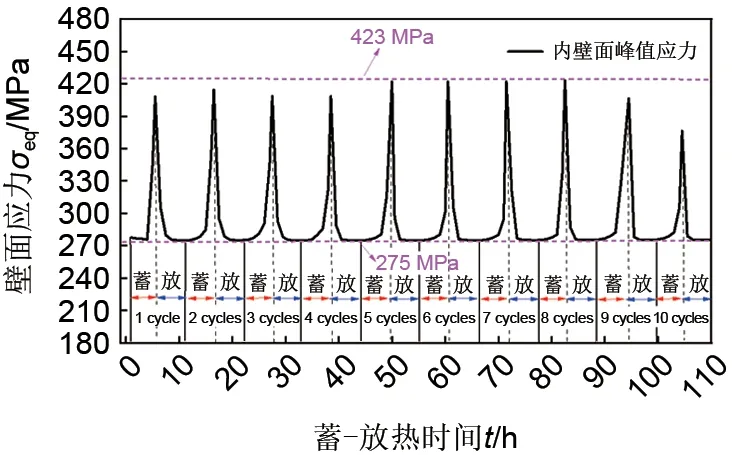
图13 给出了第1～10 次蓄-放热循环下内壁面峰值应力的变化情况。从图中可以看出，受壁面温度影响显著，连续蓄-放热循环下的内壁面峰值应力在275～423 MPa之间也呈周期性变化趋势。特别地，对于单次蓄-放热循环而言，由于蓄热时壁面温度逐渐升高，使得内壁面的峰值应力增大；放热时随着温度的降低，应力值又呈下降的变化趋势。值得注意的是，在连续的蓄-放热循环中，内壁面的峰值应力始终高于罐体材料的屈服强度167 MPa，致使蓄热罐底端的壁板与底板连接处会一直处在塑性区域。随着蓄-放热循环的进行，罐体底部极易产生低周疲劳引起的断裂失效现象，从而导致熔盐流体泄漏，严重影响CSP 系统的安全稳定运行。

4 结 论

针对单罐填充床熔盐蓄热器，利用有限容积法与有限元法构建了热-力耦合数值模型，模拟获得了多次蓄-放热循环下罐体壁面的动态温度与应力变化特性。得到的主要结论如下：

（1）罐壁温度在蓄-放热过程中呈相反的变化趋势，且在单次循环中，罐体壁面温度存在4个阶段的变化趋势：蓄热过程的急剧温升与保持稳定阶段，放热过程的缓慢下降与急剧温降阶段。在蓄热与放热的0～5 h 之内，蓄热罐筒节1～5 的壁面温度均会高于材料的蠕变阈值，进而产生高温导致的蠕变现象。

（2）蓄-放热过程中，罐壁板底端与底板连接位置极易产生应力集中导致的塑性屈服现象，但随着罐体高度的增加，壁面应力水平逐渐降低，筒节1～5 的应力值均低于材料屈服极限，仍处于弹性状态。特别地，罐体形变受安装方式与壁面温度影响显著，但最大形变量始终位于壁板顶端位置，形变最大值约为60 mm。

（3）多次蓄-放热循环中，填充床蓄热罐壁面最高温度在631～836 K 之间呈周期性变化，致使壁面也会产生周期性的高温蠕变；在长周期、低应力与高温蠕变的运行条件下，筒节1～5 的壁面损伤失效的风险增加。

3.1.2 个人出版物的海外传播现状 对于个人出版物来说，作者由于长期在某一国家从事武术教学工作，对该国的语言较为了解，能够保证语言的表达更加准确，但是出版物中的教学内容却缺乏标准。当前，许多在国外从事武术教学的教师，武术习练背景参差不齐，许多没有赴外教学许可的人员也在传播中国武术。由于教学人员自身业务素质的不足，导致其出版的纸质教材或视频影像中，教学内容不标准，动作错误频出，为中国武术的海外传播带来了阻碍。

（4）受壁面温度影响显著，内壁面峰值应力在275～423 MPa 之间也呈周期性变化趋势，且随着循环次数的增加，蓄热罐壁面的塑性损伤累积，给CSP系统的安全运行带来极大挑战。

[1] 何雅玲,杜保存,王坤,等.太阳能腔式熔盐吸热器随时空变化的光-热-力耦合一体化方法、机理分析及其失效准则研究[J]. 科学通报,2017,62(36):4308-4321.HE Y L, DU B C, WANG K, et al. Study on the coupled photonthermal-stress integration method, characteristics with time and failure criterion in the solar molten salt cavity receiver[J]. Chinese Science Bulletin,2017,62(36):4308-4321.

[2] 汪翔, 陈海生, 徐玉杰, 等. 储热技术研究进展与趋势[J]. 科学通报,2017,62(15):1602-1610.WANG X, CHEN H S, XU Y J, et al. Advances and prospects in thermal energy storage: A critical review[J]. Chinese Science Bulletin,2017,62(15):1602-1610.

[3] GAUTAM A, SAINI R P.A review on sensible heat based packed bed solar thermal energy storage system for low temperature applications[J].Solar Energy,2020,207:937-956.

[4] Libby C. Solar thermocline storage systems: Preliminary design study[R].Palo Alto,CA:Electric Power Research Institute,2010.

[5] PACHECO J E, SHOWALTER S K, KOLB W J. Development of a molten-salt thermocline thermal storage system for parabolic trough plants[J]. Journal of Solar Energy Engineering, 2002, 124(2):153-159.

[6] 尹辉斌, 丁静, 杨晓西. 高温熔融盐斜温层单罐蓄热的热过程特性[J].中国电机工程学报,2013,33(26):68-74,1.YIN H B, DING J,YANG X X.Thermal characteristics of the hightemperature molten-salt heat storage process with a thermocline in single tank[J]. Proceedings of the CSEE, 2013, 33(26): 68-74,1.

[7] XU C, WANG Z F, HE Y L, et al. Sensitivity analysis of the numerical study on the thermal performance of a packed-bed molten salt thermocline thermal storage system[J]. Applied Energy,2012,92:65-75.

[8] LI M J, QIU Y, LI M J. Cyclic thermal performance analysis of a traditional single-layered and of a novel multi-layered packed-bed molten salt thermocline tank[J]. Renewable Energy, 2018, 118:565-578.

[9] ZHAO B C, CHENG M S, LIU C, et al. Thermal performance and cost analysis of a multi-layered solid-PCM thermocline thermal energy storage for CSP tower plants[J]. Applied Energy, 2016,178:784-799.

[10]FLUECKIGER S, YANG Z, GARIMELLA S V. An integrated thermal and mechanical investigation of molten-salt thermocline energy storage[J].Applied Energy,2011,88(6):2098-2105.

[11]WANG G, YU S Y, NIU S Q, et al. A comprehensive parametric study on integrated thermal and mechanical performances of molten-salt-based thermocline tank[J]. Applied Thermal Engineering,2020,170:115010.

[12]张晓明,吴玉庭,张灿灿.大型熔盐罐结构设计、温度分布与强度分析[J].北京工业大学学报,2021,47(9):1064-1073.ZHANG X M, WU Y T, ZHANG C C. Temperature distribution and strength analysis of large-scale molten salt thermal storage tank[J].Journal of Beijing University of Technology, 2021, 47(9): 1064-1073.

[13]WAN Z J, WEI J J, QAISRANI M A, et al. Evaluation on thermal and mechanical performance of the hot tank in the two-tank molten salt heat storage system[J].Applied Thermal Engineering,2020,167:114775.

[14]Petroleum Standardization Research Institute. Welded tanks for oil storage: API Std 650 [S]. Washington: American Petroleum Institute,2013.

[15]国家市场监督管理总局, 国家标准化管理委员会. 压力管道规范工业管道 第2 部分:材料: GB/T 20801.2—2020[S]. 北京: 中国标准出版社,2020.Standardization Administration of the People's Republic of China.Pressure piping code—Industrial piping—Part 2: Materials: GB/T 20801.2—2020[S].Beijing:Standards Press of China,2020.

[16]ASME Boiler and Pressure Vessel Committee on Nuclear Power.ASME Boiler and pressure vessel code Ⅱ. Materials Part D Properties (Metric) [S]. New York: The American Society of Mechanical Engineers,2013.

[17]吴家龙.弹性力学[M].北京:高等教育出版社,2001.WU J L.Elasticity[M].Beijing:Higher Education Press,2001.

[18]姚仰平.土力学[M].2版.北京:高等教育出版社,2011.