基于BP神经网络的Stacking模型融合的光谱分类算法

摘  要：文章介绍了Stacking集成学习方法、BP神经网络模型，分别讨论了单分类器的精度，特征提取与单分类器结合的算法的精度、Stacking集成学习算法的精度。实验测试表明，以决策树、LDA、朴素贝叶斯、随机森林为基学习器，以BP神经网络为元学习器所建立的Stacking算法是最佳的光谱分类算法，该算法稳定性强，学习效果好，平均准确率高达94%。

关键词：Stacking模型融合;BP神经网络模型;多分类问题

中图分类号：TP18       文献标识码：A文章编号：2096-4706（2022）04-0091-05

Spectral Classification Algorithm of Stacking Model Fusion Based on BP Neural Network

LIN Miaofang

（South China Normal University， Guangzhou  510631， China）

Abstract： This paper introduces Stacking ensemble learning method and BP neural network model， discusses respectively the accuracy of the single classifier， the accuracy of the algorithm combining feature extraction and single classifier， and the accuracy of the Stacking ensemble learning algorithm. The experimental test shows that the Stacking algorithm established by a base learning machine of the decision tree， LDA， Naive Bayes， random forest， and a meta learning machine of BP neural network， is the best spectral classification algorithm. The algorithm has strong stability， good learning effect， and the average accuracy rate is up to 94%.

Keywords： Stacking model fusion; BP neural network model; multiple classification problem

0  引  言

分類是数据挖掘中的一个重要任务它根据提供的训练样本的辨别性特征将样本数据进行分类[1]。机器学习中的模型如决策树、LDA、朴素贝叶斯、随机森林等是常用的用于解决分类问题的模型，但这些单分类器的精度却难以得到进一步的提高。机器学习领域的分类学习模型组合集成问题已经成为适应分布式计算以及提高分类准确率而需要解决的重要课题。集成学习通过决策优化或覆盖优化等手段将若干弱分类器进行联合，以提高总体的分类性能[2]。理论可以证明，集成学习方法对于集成预测精度较高、相互独立的基学习器有很好的精度提升的效果[3]。

Stacking算法是一类典型的集成学习算法，该算法是由Wolpert提出的一种通用集成技术，也是一个重要的分类器组合模型[4]。Stacking算法将多个分类器通过某种融合策略产生更好的分类，从而实现其优越的泛化性能。在各个领域应用广泛。本文从特征提取、集成学习等多个方面出发，探究出最佳的光谱分类算法。利用光谱数据进行分类测试的结果表明，基于BP神经网络的Stacking算法是最佳的光谱分类算法。

1  Stacking集成学习方法

1.1  Stacking算法思想

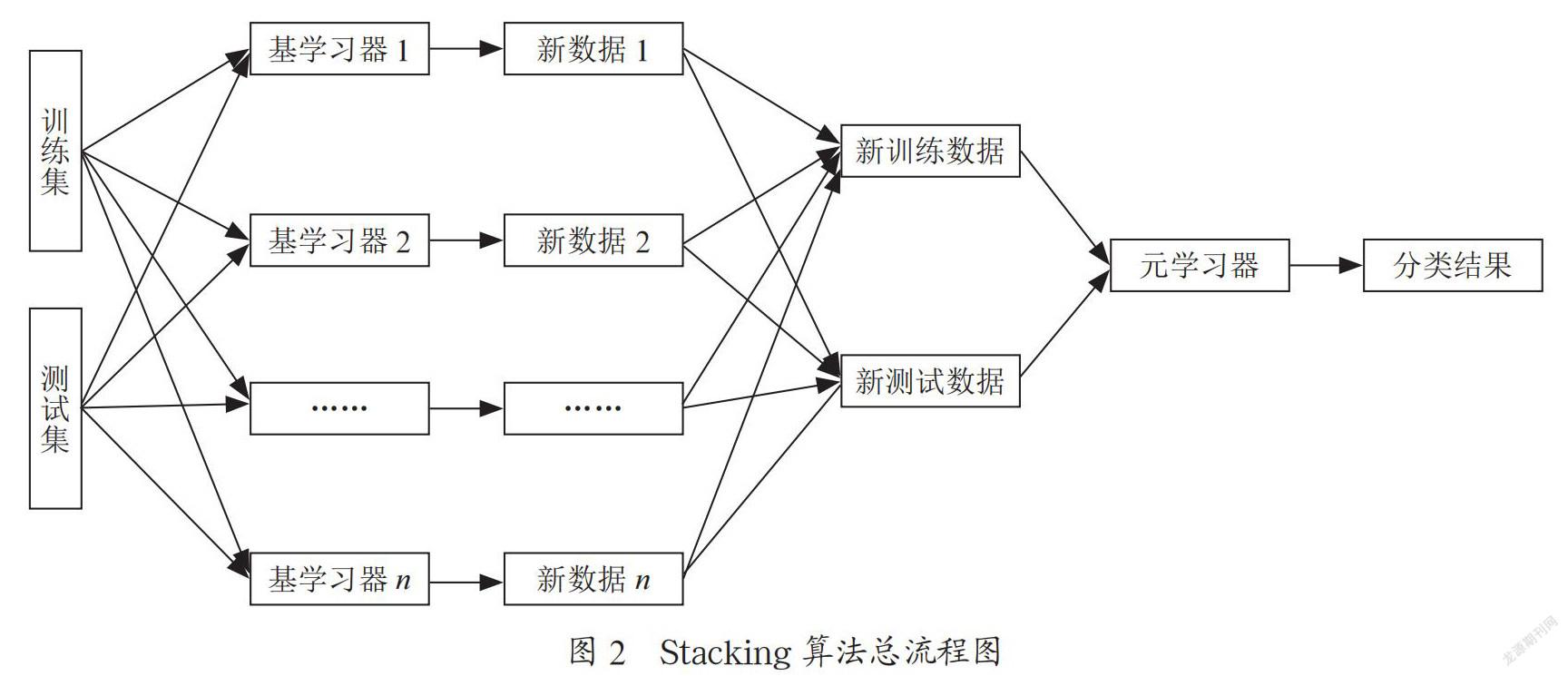
集成学习主要包括Bagging、Boosting和Stacking算法。Bagging和Boosting中的基学习器一般为同类型的学习器，而Stacking集成是异质的[5]。与Bagging和Boosting不同的是，Stacking通过学习的方式结合基分类器，以修正基分类器偏差的方式提高整个分类器的泛化能力。从结构上来看，它是一种多层的分类器的结构。基层（Base Level）的分类器即为基分类器，元层（Meta Level）的分类器称为元分类器。Stacking算法的主要思想是：通过基分类器将数据进行分类，再将基分类器输出的分类结果作为元分类器的输入结果进行分类，从而达到最终的分类结果。

1.2  Stacking算法流程

为了防止过拟合，本文使用交叉验证的方式来训练基学习器。基于光谱数据和Stacking算法的步骤为[3]：

Algorithm 1 Stacking Algorithm

输入：训练数据集（200×481）    测试数据集（159×481）

基学习器Ni（i=1，…，n）元学习器M

分类类别数m

输出：分类结果

（1）对每一个基学习器Ni，利用训练集数据，进行K折交叉验证，获得n个训练集的特征矩阵，将这n个矩阵的信息进行合并，即按列进行合并，得到新的训练集数据D1;

（2）在进行交叉验证的同时，对测试集进行预测，从而得到由一个基学习器学习得到的K种预测数据，将该预测数据取平均，作为基学习器对测试集的最终预测结果。与步骤一类似，我们会得到n个训练集的特征矩阵，将这n个矩阵的信息进行合并，即按列进行合并，得到新的测试集数据D2;

（3）将步骤一和步骤二得到的新的训练数据集D1对元分类器进行训练。再利用新的测试数据D2以及训练好的元分类器，对测试集进行预测，得到最终的分类结果。

在基于Stacking的分类问题中，对于基分类器的输出结果，一般不直接输出分类结果，因为分类的结果并没有办法取平均，或者说，对类别取平均是没有意义的。一个可行的解决方法是，输出对各类别的判断概率。在Python的机器学习模块中，在每个分类器的内部，会计算分类器对样本的每个类别的概率，从而将最大概率所在的类作为结果输出。由此，本文将基分类器对每个样本的各类别的判断概率作为预测的输出结果。

Stacking算法的示意图如图1和图2所示。

2  BP神经网络模型

2.1  BP神经网络定义及结构

BP神经网络的定义是：采用误差反向传播算法（BP：Error Back-propagation Algorithm）的多层前反馈人工神经网络。

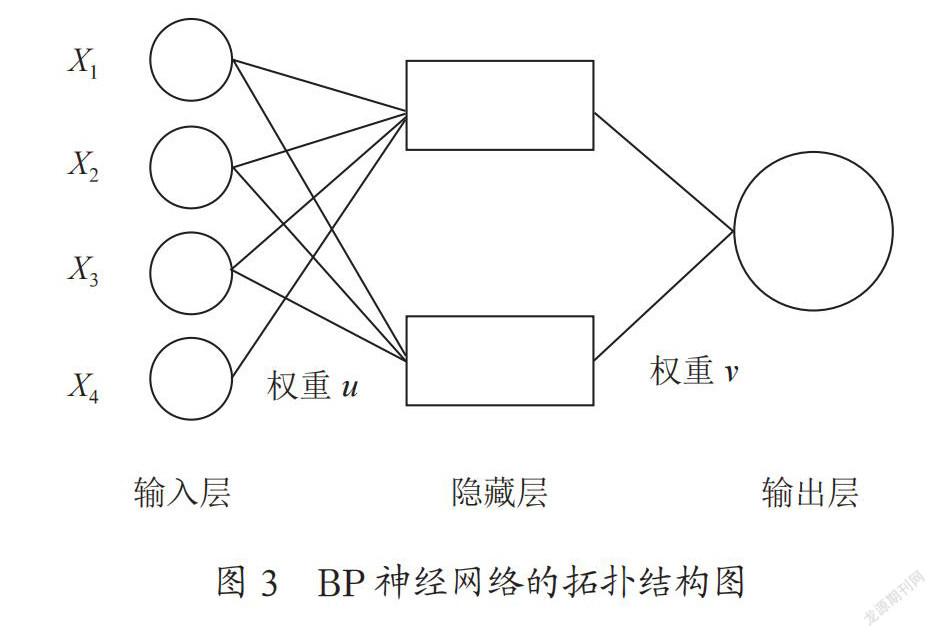
BP神经网络通常由输入层、隐含层和输出层组成，层与层之间全互联，每层节点之间不相连。它的输入层节点取训练样本的特征维数，输出层节点的个数取类别的个数。隐藏层节点目前尚无确定的标准。

具有一个隐藏层的BP神经网络的拓扑结构如图3所示。

2.2  BP神经网络思想

BP算法的基本思想是把学习过程分为两个阶段：第一阶段（正向传播过程），给出输入信息通过输入层经各隐层逐层处理并计算每个单元的实际输出值;第二阶段（反向过程），若在输出层未能得到期望的输出值，则逐层递归地计算实际输出与期望输出之间的差值（即误差），通过梯度下降法来修改权值，使得总误差函数达到最小[6]。

2.3  BP神经网络算法步骤

BP神经网络的算法步骤为[6]：

Algorithm 2 Back Propagation Neural Network

（1）权值初始化：wij=Random（）   wjk=Random（）;

（2）依次输入训练样本集。设当前输入为第p个样本;

（3）依次计算各层的输出：xj，yk，j=0，1， …，n1  k=0，1，…，m-1

（4）求各层的反向传递误差：;

（5）记录已学习过的样本数p。如果p

（6）按权值修正公式修正各层的权值和阈值;

（7）按新的权值在计算xj（p），yk和EA，若对每个p和k都满足|dk（p）-yk（p）|< ε，或达到最大迭代次数，则终止训练。否则转到第二步继续新一轮的学习训练。

设BP神经网络的输入矢量为XRn，其中X=（x1，x2，…，xn）T;隐藏层含有n1个神经元，它们的输出为XRn1，X=（x1，x2，…，xn）T;输出层有m个神经元，输出yRm，y=（y0，y1，… ，ym-1）T。输入层到隐藏层的权值为wij;隐藏层到输出层的权值为wjk。

设训练样本集有P个样本，对应的期望输出（即真实类别）为d（1），d（2），…，d（p），设当所有样本都输出一次后，总误差为EA=（dk（p）-yk（p））2。

BP神经网络算法流程如图4所示。

3  光谱分类最佳算法探究

本文使用光谱数据进行光谱分类。其中，测试集样本共有200条，含有481个特征，训练集样本共有159条，含有481个特征。

3.1  单分类器分类性能

本文选取四种分类算法：LDA线性判别分析算法、决策树算法、随机森林算法、朴素贝叶斯算法。在不进行集成学习的情况下，分别讨论上述四种分类算法对光谱数据分类的准确率。

分别利用Python的sklearn库中的函数，利用训练集和测试集分别进行5次分类预测，将5次的准确率取平均作为单分类器的分类准确率。测试结果如表1所示。

分析测试结果，可以得出结论：随机森林算法的准确率较高。

3.2  基于单分类器的特征维数讨论

由于数据集的特征维数较多，可能导致噪声较大，对分类的效果可能会有影响。因此，本文在单分类器的基础上，对数据进行降维，讨论维数对上述四种分类器的分类性能的影响。

首先，本文利用主成分分析法对数据进行降维。利用Python编写主成分分析法的程序，对数据集进行降维，并生成降维后的新的数据集。

为了能够尽可能减小降维后的主成分损失的信息，本文选取的主成分的累積贡献率规定高于85%。本文摘取一部分数据进行展示，如表2所示，并由此决定我们要将数据降到多少维。

表2  主成分累积贡献率表

接下来，本文将进行以下测试：将光谱数据集分别降到20，25，30，35，…，100维，分别测试四个单分类器的准确率。注意，单分类器的准确率均为多次测量取平均值得到的结果，绘制出准确率随维度的变化趋势图，如图5所示。

分析测试结果，可以得出以下结论：

当使用主成分分析对数据进行降维时，单分类器的准确率的峰值均高于降维前的准确率。若采用基于主成分分析的单分类器对光谱数据进行分类，效果较好的是LDA线性判别分析法和朴素贝叶斯分类法。

3.3  多分类器融合的Stacking算法

在3.1和3.2节，本文分别探讨了单分类器的分类性能以及特征降维后的分类性能。在本节，将讨论多分类器融合的Stacking模型的分类性能。

3.3.1  基学习器的选取

在本文中，选取LDA线性判别分析模型，决策树，随机森林以及朴素贝叶斯分类器作为基学习器。

3.3.2  元学习器的选取

在本文中，分别讨论将LDA线性判别分析，BP神经网络模型作为元学习器的Stacking模型的分类性能。

3.3.3  将LDA作为元学习器的Stacking模型

利用Python实现Stacking算法，并将LDA作为Stacking算法的元学习器，利用未降维的光谱数据进行训练，并对光谱数据进行分类。多次测量分类的准确率从并且取平均值。最终得到的分类准确率为82%。

与单分类器进行对比，可以得出结论：将LDA作为元分类器的Stacking分类器融合模型的分类性能明显高于单分类器。

3.3.4  将BP神经网络作为元学习器的Stacking模型

利用Python实现BP神经网络算法，并将BP神经网络作为Stacking算法的元学习器，对光谱数据进行分类，并且多次测量取平均值。

本文实现BP神经网络时，将Sigmoid函数作为激励函数。由于本文选取了四个分类器作为基分类器，每个基分类器得到的新特征数据的维度为7，因此设置输入节点为28个。并设置隐藏层节点为10个，输出节点为7个。最终得到的分类准确率为94%。

与单分类器和基于LDA的Stacking模型相比，将BP神经网络模型作为元学习器的Stacking模型的分类性能大大提升，达到了94%。因此，基于BP神经网络模型的Stacking模型的分类性能最佳。

3.4  基于BP神经网络的Stacking模型的其他讨论

在3.1节中，本文提到BP神经网络隐藏层节点目前尚无确定的标准。因此本文将在此节探讨最佳的隐藏层节点个数。除此以外，由于光谱数据集特征较多，本文将在此节探讨最佳的特征维数。

3.4.1  隐藏层节点最佳个数的探讨

本文分别测试隐藏层节点为5，6，7…，15的模型的准确率，并绘制变化趋势图，如图6所示。可以看出，当隐藏层节点个数为5时，基于BP神经网络的Stacking模型的分类性能较佳。

3.4.2  最佳特征维数的选取

本文将进行以下测试：将光谱数据集分别降到20，25，30，35，…，100维，设置BP神经网络的隐藏层节点个数为5，分别测试基于BP神经网络的Stacking模型的准确率，并且多次测量取平均值得到的结果。绘制出准确率随维度的变化趋势图，并标出最佳的特征维数，如图7所示，可以得到最佳的特征维数为85。

4  结  论

通过对多种分类算法策略的探究，可以得出以下结论：当使用单分类器时，分类效果较好的是随机森林算法。当对数据进行降维后，各个单分类器的最佳分类准确率均有所上升。此时，分类效果较好的单分类器是LDA模型和朴素贝叶斯分类器。相较于单分类器，将多种分类器融合的Stacking算法效果更佳。当选取LDA模型作为Stacking算法的元学习器时，分类的准确率可达到82%。当选取神经网络作为Stacking算法的元学习器时，分类的准确率可达到94%。在数据未降维的情况下，将BP神经网络的隐藏层节点设置为5个时，Stacking模型的分类准确率最佳，平均可达95.1%。当BP神经网络的隐藏层节点设置为5个时，利用主成分分析法对数据进行降维。当数据维度降至85维时，Stacking模型的分类准确率最佳，平均可达96.2%。综上所述，基于BP神经网络的Stacking算法是最佳的光谱分类算法。

参考文献：

[1] 何丽，韩文秀.用元决策树组合多个分类器的方法 [J].计算机工程，2005（12）：18-19+80.

[2] 秦飛.基于半监督学习的文本分类研究 [D].四川：西南交通大学，2010.

[3] 李昆明，厉文婕.基于利用BP神经网络进行Stacking模型融合算法的电力非节假日负荷预测研究 [J].软件，2019，40（9）：176-181.

[4] 包志强，胡啸天，赵媛媛，等.基于熵权法的Stacking算法 [J].计算机工程与设计，2019，40（10）：2885-2890.

[5] 曹婷婷，张忠林.代价敏感的KPCA-Stacking不均衡数据分类算法 [J].计算机工程与科学，2021，43（3）：525-533.

[6] 孙娓娓.BP神经网络的算法改进及应用研究 [D].重庆：重庆大学，2009.

作者简介：林苗芳（2002.02—），女，汉族，广东汕尾人，本科在读，研究方向：信息与计算科学。