时间尺度上具有次线性中立项的三阶Emden-Fowler时滞动力方程的振动性
2022-07-06仉志余冯瑞华
仉志余, 冯瑞华
(1. 太原工业学院理学系,太原 030008; 2. 中北大学理学院,太原 030051)
0 引言
本文研究时间尺度T 上具有次线性中立项的Emden-Fowler 时滞动力方程
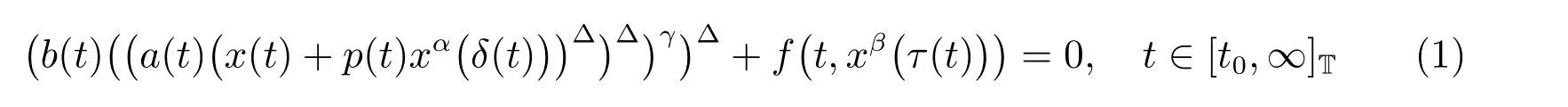
的振动性。除非特殊声明,下面的假设总成立:
(A1)a(t)> 0, b(t)> 0, p(t)≥0, q(t)> 0 是定义在[t0,∞)T= [t0,∞]∩T 上的实值右稠连续函数,连续函数f(t,u)满足f(t,u)/u ≥q(t), u ̸= 0,并有a∆(t)≤0,0≤p(t)≤p<1;
(A2)α、β、γ均为两个正奇数之比的常数且0<α ≤1, γ ≤β;
(A3)δ(t)和τ(t)是定义在[t0,∞)T上的时滞函数,满足τ(t)≤t, δ(t)≤t,且有τ∆(t)>0,limt→+∞τ(t)=limt→+∞δ(t)=∞。
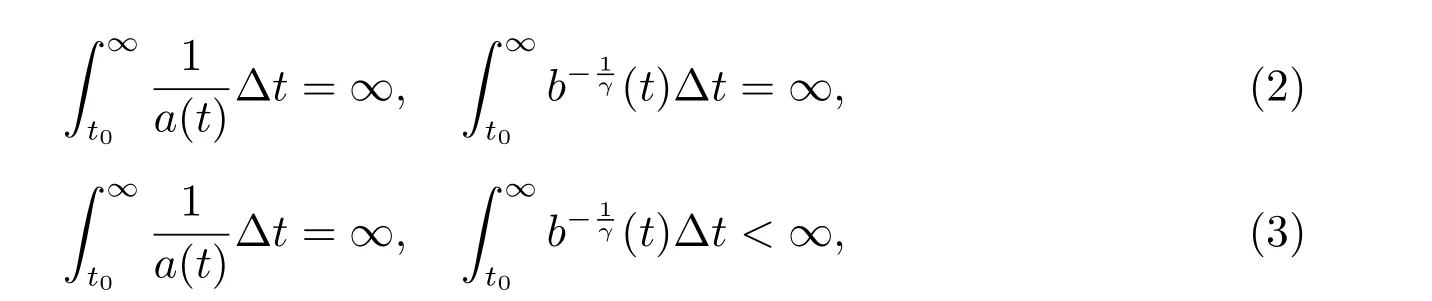
本文将分别在两种情况下建立方程(1)的振动定理。
本文仅考虑方程(1)的非平凡解x(t),即对于一切T ≥Tx ≥t0,使得sup{|x(t)|:t ∈[T,∞)T}>0 的解。因为我们研究的是方程解的振动性,所以假设时间尺度T 是无界的。如果x(t)既不是最终正解,也不是最终负解,则称x(t)为振动的,否则称x(t)为非振动的。如果方程(1)的每一个解都是振动的,则称其为振动的,否则称为非振动的。
人们对于时间尺度上时滞动力方程振动性研究的兴趣经久不衰,这是因为它们有着广泛的工程背景和应用价值,可见文献[1—4]所述。而在科学工程等领域的应用研究中时滞现象是普遍存在的,据文献[2]可知,在研究控制理论、物理学、电动力学以及光学等非线性系统的定性、定量行为时,建立的数学模型都需要考虑“时滞”现象。如在自动控制的装置中,从输入信号到接收到反馈信号,必然要有一段时间滞后;又如生物医学中一些传染病模型等也具有时滞现象;再如桥梁等建筑物体受外力冲击产生的振动和车辆行驶中产生的振动都有时滞现象。因此,需建立中立型时滞动力方程模型进行刻画。除此之外,还需要考虑系统的离散性引起的影响。总之,时间尺度上的动力方程理论就能更好地解决这些困难,使我们更好地理解连续系统与离散系统以及其他复杂系统的本质特征。因此,研究时间尺度上中立型时滞动力方程的振动性具有广泛的应用价值。
关于中立型时滞动力方程及其中立项的类型,一般按其难度是从线性到非线性的。次线性和超线性是非线性的常见类型。具有线性中立项的二阶方程的振动性研究成果已相当丰富[5–9],但具有次线性或超线性中立项的研究成果因受其难度的影响就比较少见[10–14]。例如,2007 年,Lin 和Tang[11]研究一阶具有超线性中立项的微分方程

的振动性。2014 年,Agarwal 等[12]研究了一类具有次线性中立项的二阶时滞微分方程
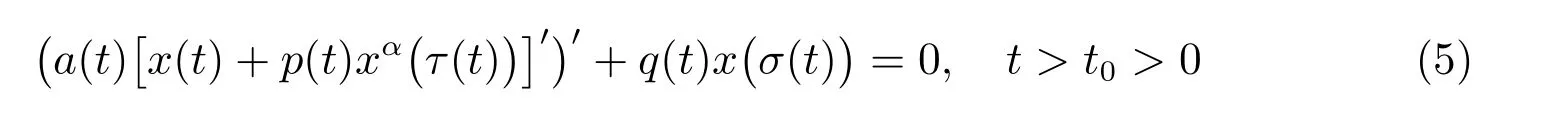
的振动性,这里0<α ≤1 是两个正奇数的比。2017 年,Tamilvanan 等[13]研究了具有次线性中立项的二阶非线性微分方程
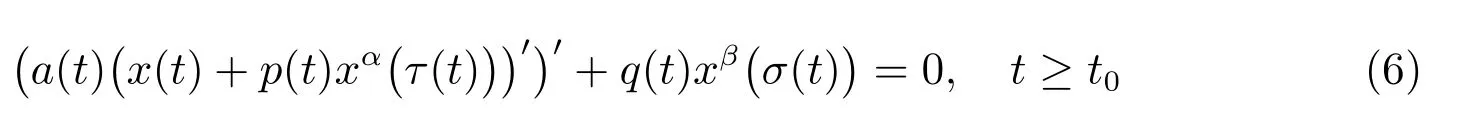
的振动性,这里α和β是两个正奇数的比值。2018 年,Grace 和Graef[14]巧妙地运用了不等式技术也研究方程(6)的振动性,并得到了方程振动的充分条件。
由于三阶中立型动力方程的振动性情形更为复杂,所以其研究成果如文献[3,4,15—22]远没有一二阶的那么丰富,其中具有次线性中立项的也只有文献[21—22],他们研究的是一类具有次线性中立项的三阶时滞微分方程
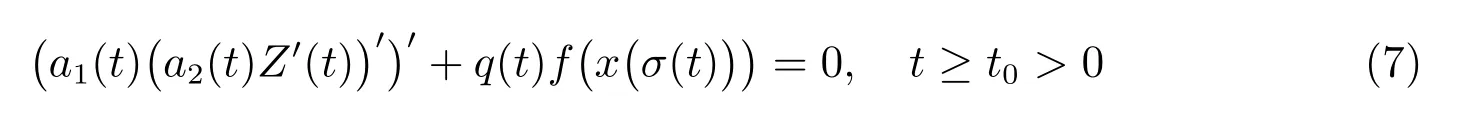
的振动性,其中Z(t) =x(t)+p(t)xα(τ(t)),0<α ≤1 是两正奇数的比。ai(t)(i=1,2)、p(t)、q(t)是正实值连续函数,τ(t)、σ(t)是时滞函数,满足τ(t)≤t, σ(t)≤t且limt→+∞τ(t) = limt→+∞σ(t) =∞。此外,函数f(u)非减且对于u ̸= 0 存在常数k满足uf(u)≥k> 0。他们分别得到了如下两个振动定理,即文献[22]中定理1 和定理2。
定理1 设0 成立。如果存在一个正值函数ϕ ∈C1([t0,∞),R),使得对任意常数M> 0 和所有足够大的t3>t2>t1>t0,有 成立,其中 则方程(7)的每个解x(t)振动或者limt→∞x(t)=0。 定理2 设0 成立。如果存在一个正值函数ϕ ∈C1([t0,∞),R),使得对任意常数M> 0 和所有足够大的t3>t2>t1>t0,有(9)式、(10)式和 成立,其中 则方程(7)的每一个解x(t)振动或者limt→∞x(t)=0。 对于时间尺度上三阶中立型动力方程振动性研究也只见到中立项是线性,即α=1 的情形。如2014 年,Candan[18]研究了时间尺度上具有线性中立项的三阶非线性时滞动力方程 的振动性,这里0≤p(t)≤p< 1, γ ≥1 是两个正奇数的比,r1(t)、r2(t)、p(t)是正实值右稠连续函数,τ(t)、δ(t)是时滞函数满足τ(t)≤t, δ(t)≤t且有limt→+∞τ(t) =limt→+∞δ(t)=∞和δ∆(t)>0 成立。此外,连续函数f:T×R→R 满足对所有u ̸=0 都有uf(t,u)> 0,且存在正实值右稠连续函数q(t),使得|f(t,u)|≥q(t)|uγ|。文献[18]得到了多个振动定理,现将其中定理2.1 和定理2.2 改述为下面的定理。 定理3 设δ(σ(t))=σ(δ(t)),其中σ(t)特指时间尺度T 的右跳算子。如果 成立,其中Q(s)=q(s)(1−p(s))γ,则方程(13)的每个解y(t)振动或limt→∞y(t)=0。 定理4 设δ(σ(t)) =σ(δ(t))且(14)和(15)式成立,若存在一个正实值右稠连续且∆可微函数α(t),使得 则方程(13)的每个解y(t)振动或者limt→∞y(t)=0。 显然,方程(7)和(13)都是方程(1)的特例。受到文献[18]关于处理时间尺度和文献[21—22]关于处理次线性中立项方法的启发,我们利用不同于文献[21—22]的不等式方法研究方程(1)分别在(2)式和(3)式情况下的振动性,拓展并改进上述已有结果。 为了方便引入下面的记号 引理1[5]如果A>0, B ≥0, u>0,则有 而当且仅当B=A时上式等号成立。 引理2 设x(t)是方程(1)的最终正解且(2)式成立,则z(t)有且仅有以下两种情形之一: (I)z(t)>0, z∆(t)>0,(a(t)z∆(t))∆>0,(b(t)((a(t)z∆(t))∆)γ)∆<0; (II)z(t)>0, z∆(t)<0,(a(t)z∆(t))∆>0,(b(t)((a(t)z∆(t))∆)γ)∆<0。 证明 证明过程与文献[18]中的引理1 类似,故省略。 引理3 设x(t)是方程(1)的最终正解且(3)式成立,则z(t)有且仅有(I)、(II)和: (III)z(t)> 0, z∆(t)> 0,(a(t)z∆(t))∆< 0,(b(t)((a(t)z∆(t))∆)γ)∆< 0,三种情形之一。 证明 证明过程与文献[22]中的定理2 类似,故省略。 引理4 设z(t)满足引理2 的情形(I)且a∆(t)≤0 和 所以可得z∆∆(t)>0。 令Z(t)=z(t)−tz∆(t),有 可知Z(t)在[t1,∞)T上是严格单调减的。可以断言,存在t2∈[t1,∞)T,当t ∈[t2,∞)T时,Z(t)>0。否则若Z(t)<0,于是 从而,有z(τ(t))≥Lτ(t)。由于z(t)> 0, z∆(t)> 0, z∆∆(t)> 0,可知z(t)是无界的,所以x(t)也是无界的。于是,存在常数P> 0,使得x(t)≥Pz(t)。进而有x(τ(t))≥Pz(τ(t))。所以将其代入方程(1),得 对上式从t3到t积分,有 可得(21)式成立,从而有 即(22)式成立。 定理5 设(2)式成立,若存在可微函数ρ(t)∈(T,R),使得对任意常数M ∈(0,1](当α=1 或β=γ时,M=1)和所有足够大的t1≥t0>0,均有 则方程(1)的每个解x(t)振动或者limt→∞x(t)=0。 证明 设方程(1)在[t0,∞)T上有一个非振动解x(t),不妨设最终为正(最终为负时,可类似证明),且存在t1∈[t0,∞)T,使得t ∈[t1,∞)T时,有x(t)> 0, x(τ(t))>0, x(δ(t))>0。由引理2 知,z(t)存在两种可能的情形。 假设z(t)满足情形(I),则当t>t1时,有z(t)> 0, z(τ(t))> 0, z(δ(t))> 0。因为z(t)在[t1,∞)T是单调增的,所以有z(t)>M0=min{z(t1),1}∈(0,1],从而有 显然,当α=1 时,在上式中取M0=1 仍成立。从而有 将(25)式代入方程(1),有 定义Riccati 变换 显然,有ω(t)>0,由时间尺度上积与商的求导法则及(26)式、(27)式,可得 从而,有 其中 根据Keller 链锁法则公式(可见文献[4]引理1)并注意到这里z∆(t)>0,有 于是,当β>1 时,有 令 将上式代入(28)式并注意到(22)式和(27)式,则 由z(t)在[t1,∞)T是单调增的,知z(t1) 当0<β ≤1 时,由(29)式知 因此,将上式代入(28)式,有 再将z(τ(σ(t)))>M0代入上式,得 根据c(t)的定义,合并(31)和(32)两式,得 根据不等式(18),在(33)式中令 这与(23)式矛盾。 于是,有x(τ(t))>kz(τ(t)),将其代入方程(1),得 对上式从t到∞积分,并注意到zβ(τ(t))≥lβ,可得 进而,有 再对上式从t到∞积分,得 又对上式从t1到∞积分,有 这与(24)式矛盾,则l=0。故有limt→∞x(t)=0。 注1 由定理5 知,选择不同的函数ρ(t),可得到方程(1)多个不同的振动定理,这里不一一列出了。特别指出,当ρ(t) = 1, α= 1, γ=β时,可得定理3。因此,本文定理5 已包含了文献[18]中的定理2.1。 注2 当α= 1, β=γ时,方程(1)退化为方程(13),即使此时本文定理5 也包含了定理4 即文献[18]中的定理2.2,因为定理4 中的R2(t,t1)就是本文的B(t,t1)。 注3 即使当T=R, γ=β=1,方程(1)退化为方程(7)时,本文定理5 比定理1 即文献[22]中的定理1 更简洁,且这里已将文献[22]中的任意常数M> 0 改进为任意常数M ∈(0,1],γ=β=1 拓展为β ≥γ>0。 定理6 设(3)式、(23)式和(24)式成立。若对于足够大的t1>t0,还有 成立,其中 则方程(1)的每个解x(t)振动或者limt→∞x(t)=0。 证明 设方程(1)在[t0,∞)T上有一个非振动解x(t),不妨设最终为正(最终为负时,可类似证明),则存在t1∈[t0,∞)T,使得t ∈[t1,∞)T时,有x(t)> 0, x(τ(t))>0, x(δ(t))> 0,由引理3 知z(t)存在三种可能情形。假设z(t)满足情形(I)或者情形(II),则与定理5 的证明相同得方程(1)的解x(t)振动或者limt→∞x(t)=0。 假设z(t)满足情形(III),则a(t)z∆(t)> 0, b(t)((a(t)z∆(t))∆)γ在[t1,∞)T上是单调减,所以,对l>t ≥t1,有 从而,有 若令 则有 对V(t)求导并注意到(26)式成立,则得 将上式代入(36)式,得 当0<γ ≤1 时,根据Keller 链锁法则公式(类似于(29)式),有 将上式代入(39)式,得 其中 将(38)式代入上式,并注意到V(t)<0,得 即有 因为z(t)> 0 单调增,B(t)> 0 单调减且趋于0,所以存在t2≥ t1,使得当t ∈[t2,∞)T时,有z(t)≥B(t),从而有 又由(41)和(42)式,可得 将上式代入(40)式,得 当γ>1 时,类似于(43)式的推导,可得 在上式中,以s代替t,两边同乘以Bγ(σ(s)),并对s从t2到t积分,得 对(44)式左边用分部积分,可得 对于上式中的(Bγ(s))∆利用Keller 链锁法则,注意到这时B∆(s)≤0,有 当0<γ ≤1 时,由上式以及(44)和(45)式,同时注意到V(s)<0,可得 根据不等式(18),在(46)式中取 因此,有 将上式代入(46)式,并注意到(35)式,得 显然这与(34)式矛盾。 当γ>1 时,与(46)式证明类似,可得 在(47)式中令 再次利用不等式(18),得 将上式代入(47)式,有 显然这与(34)式矛盾。 注4 同注3 知,当T = R, γ=β= 1 时,(34)式就是(12)式,且M ∈(0,1]更精细。因此,本文定理6 包含并改进了定理2 即文献[21]中的定理1 和文献[22]中的定理2。 例1 考虑时间尺度T 上具有次线性中立项的三阶非线性时滞动力方程 取ρ(t)=1 时,有 亦即(24)式成立。因此,由定理5 知,方程(48)在[1,∞)T上的解x(t)振动或者limt→∞x(t)=0。 但显然定理3 和定理4 对方程(48)无效,因为这里γ ̸=β。 例2 考虑时间尺度T 上具有次线性中立项的三阶非线性时滞动力方程 所以(51)式成立,从而根据定理6 知,方程(50)的解x(t)在[1,∞)上是振动的或limt→∞x(t)=0。 但是,即使当T = R 时,定理2 即文献[21]定理1,文献[22]定理2 以及本文所列文献中的结果均对此例无效。 本文研究了时间尺度上具有次线性中立项的三阶Emden-Fowler 时滞动力方程(1)的振动性,利用Riccati 变换和不等式技巧,分别在正则((2)式)和非正则((3)式)条件下建立了方程(1)的新振动准则定理5 和定理6,所得结果包含和改进了以往文献的相应结果,最后列举应用实例验证了所得理论结果的有效性。 本文主要的创新点或突破点在于将类似于过往文献中Candan 方程(13)的α= 1 拓展到了方程(1)的0<α ≤1,这揭示了具有线性中立项(α= 1)和真次线性中立项(0<α< 1)时方程的振动性对函数p(t)的不同要求。前者只需0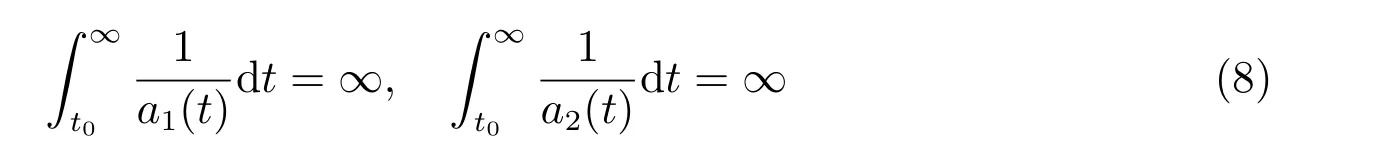

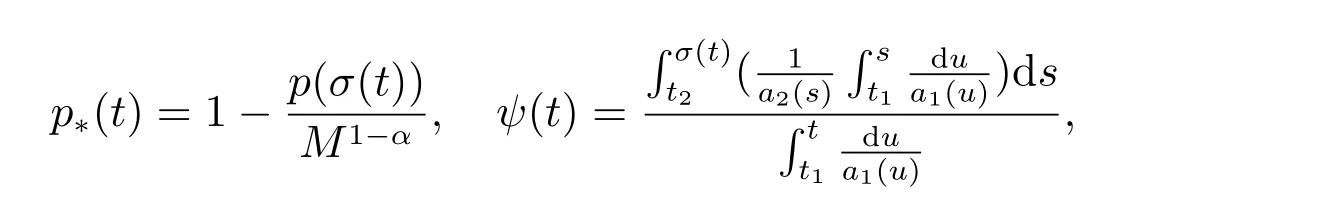
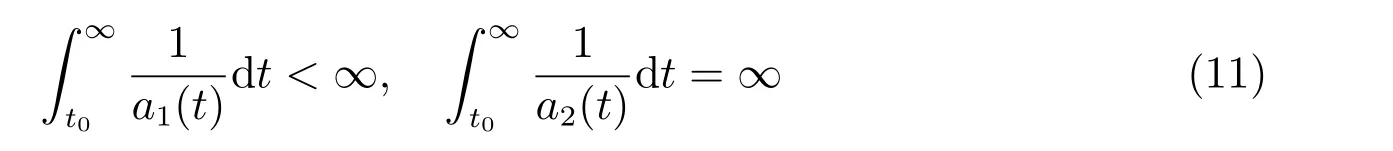

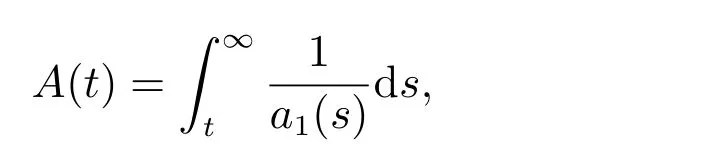
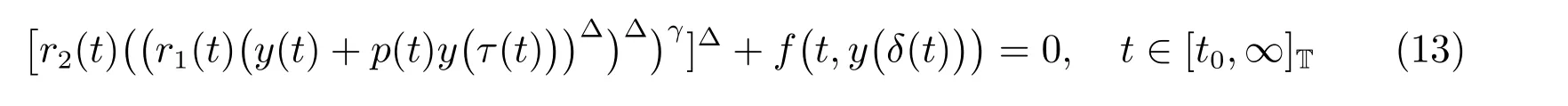


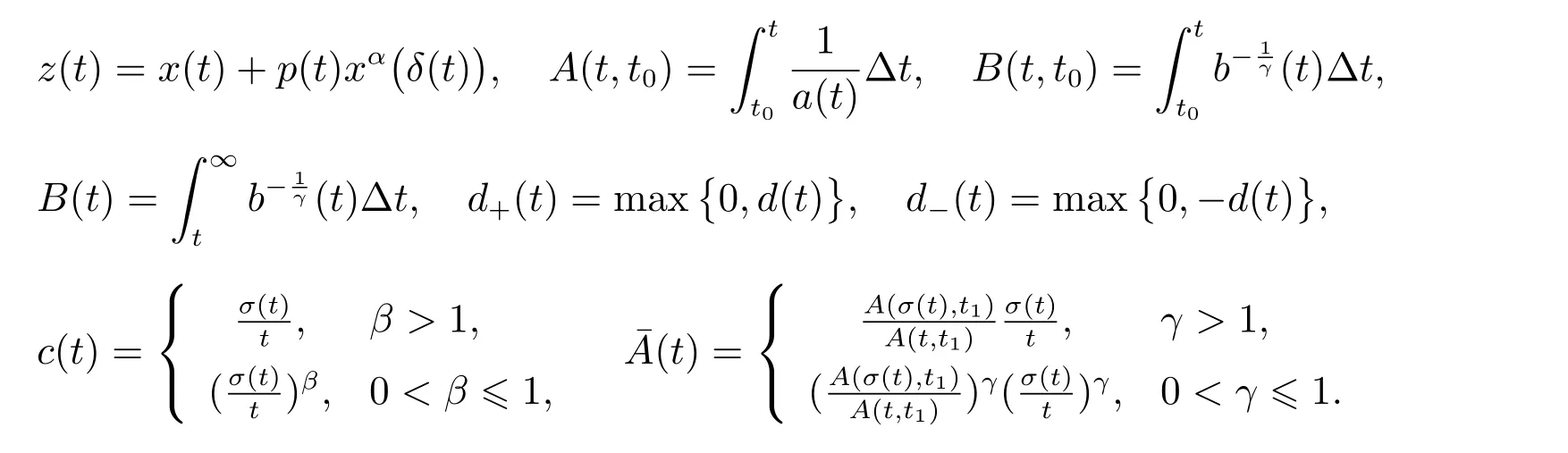
1 重要引理
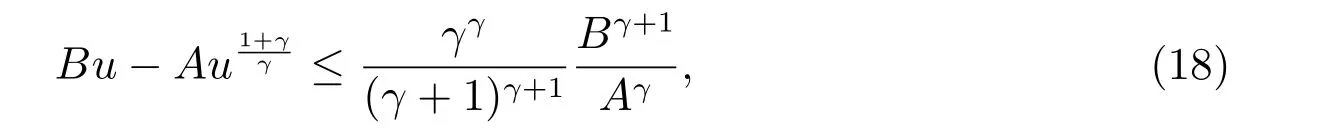
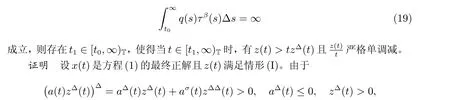
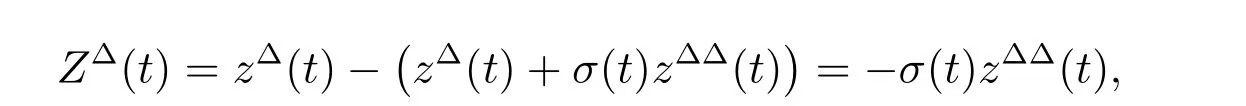



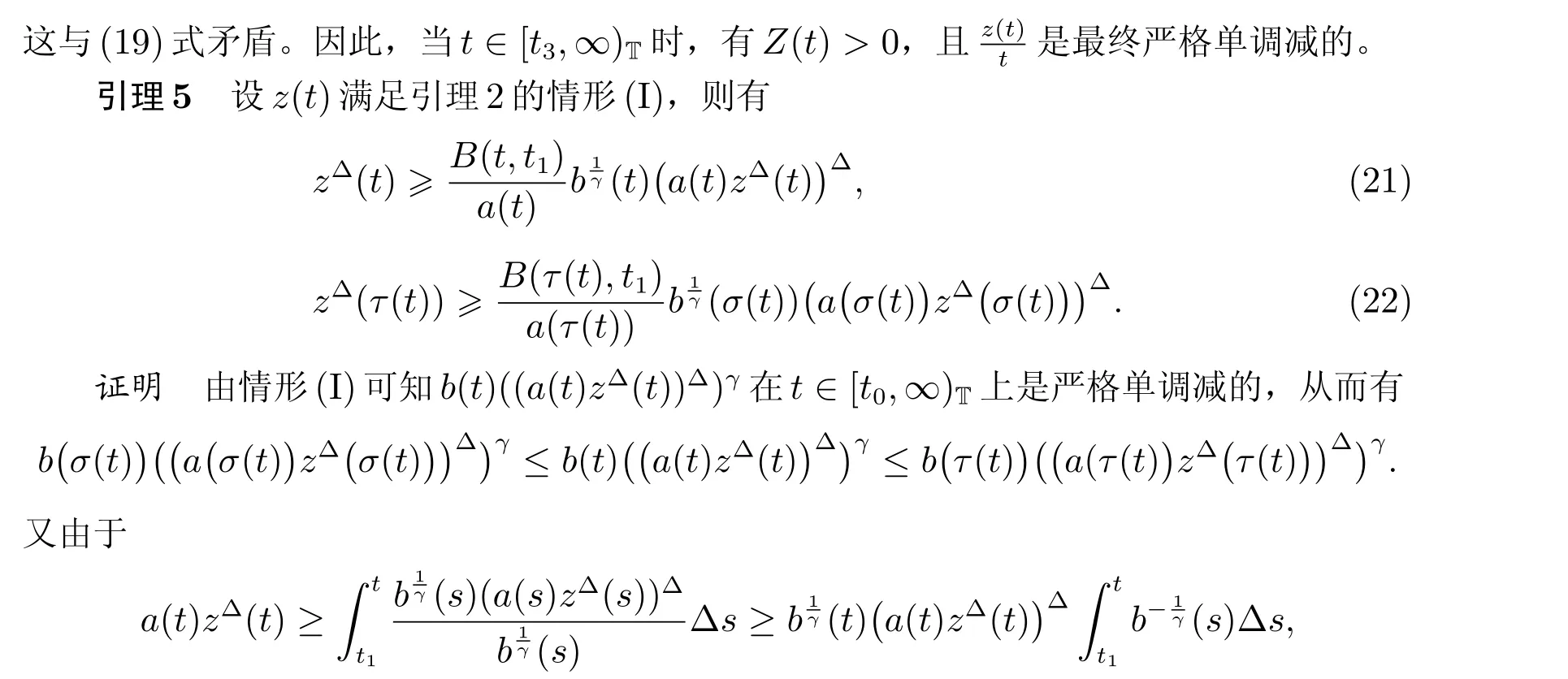
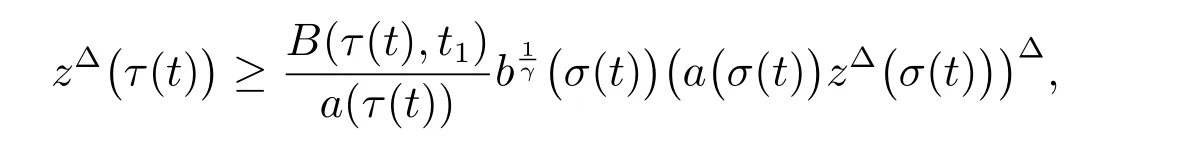
2 主要结果与证明
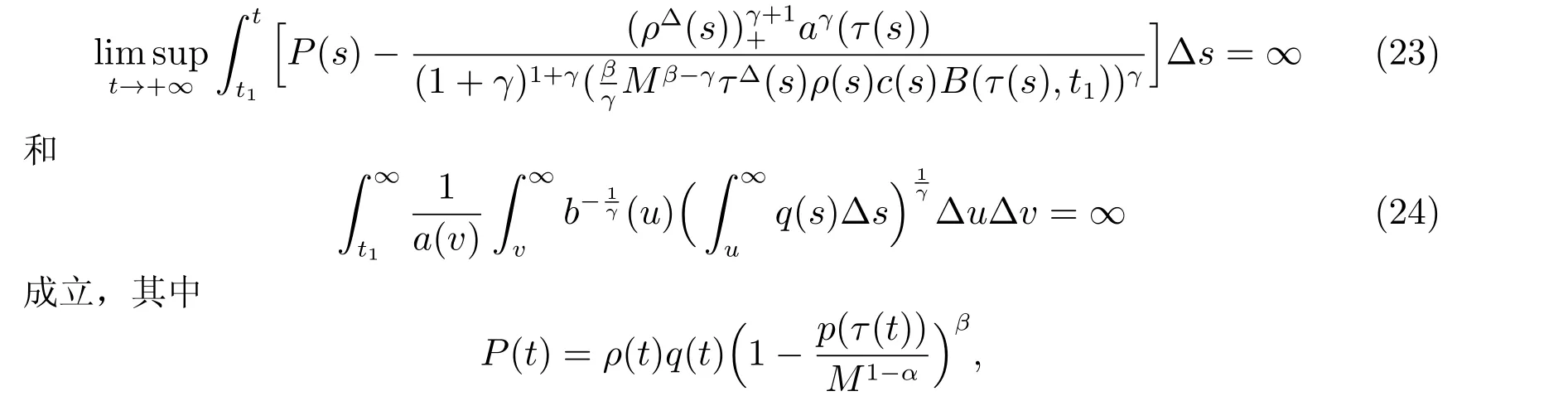

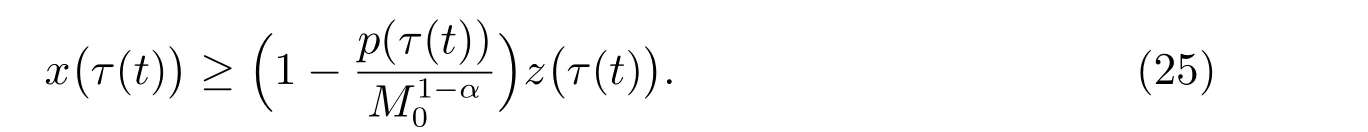
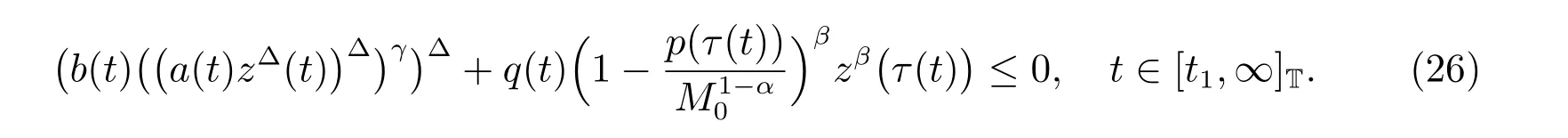
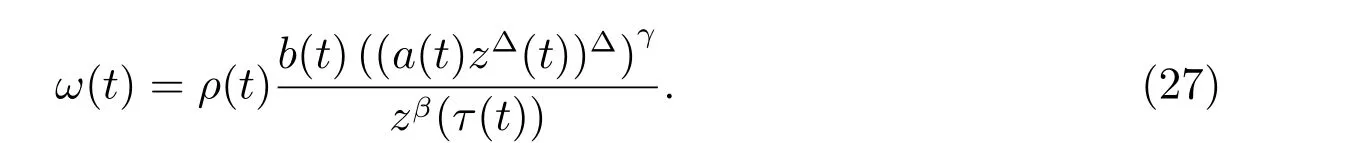
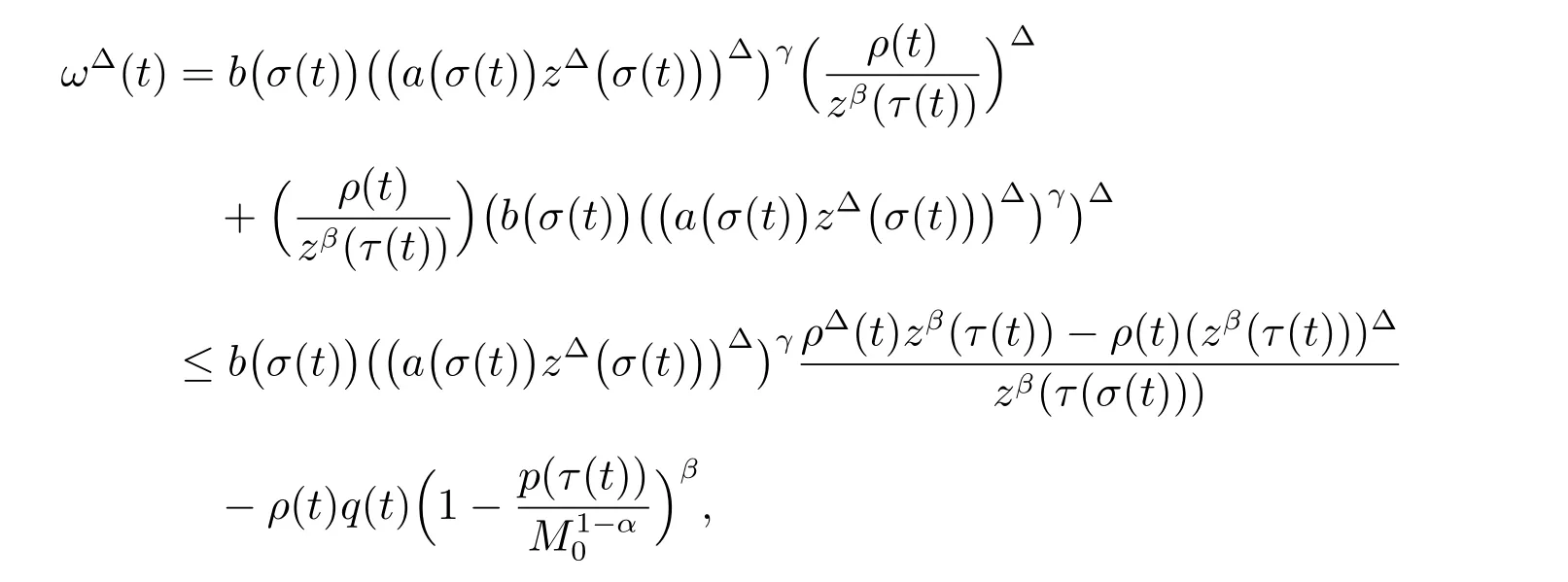
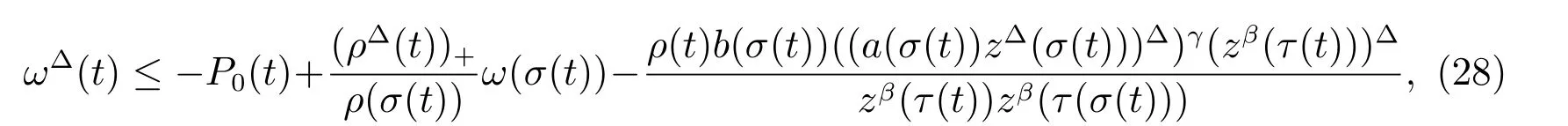
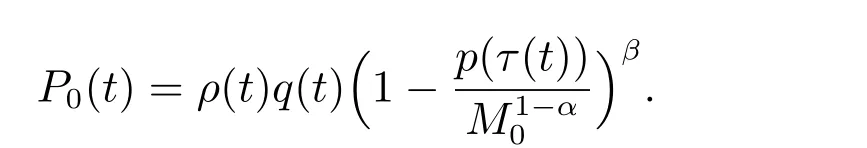
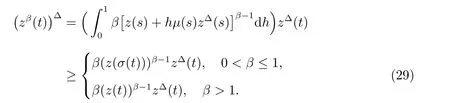
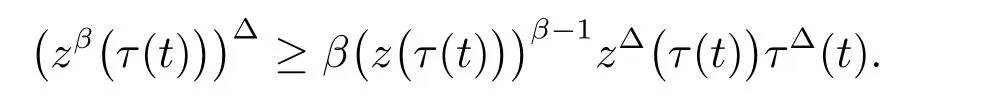

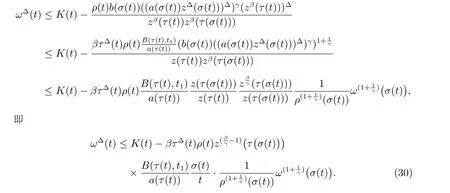
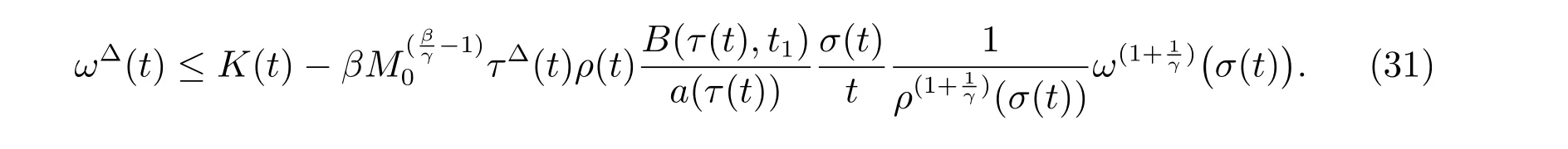

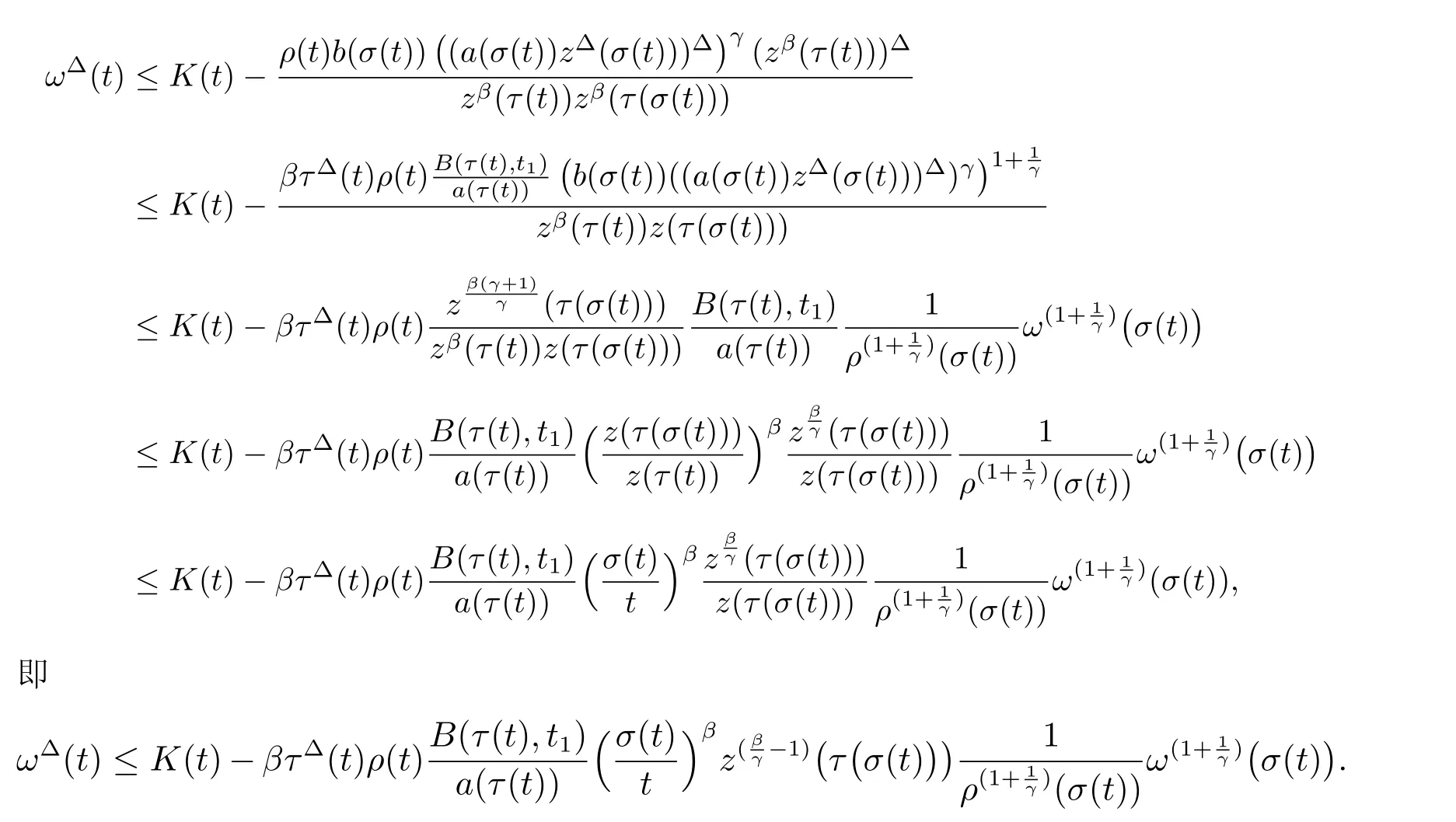
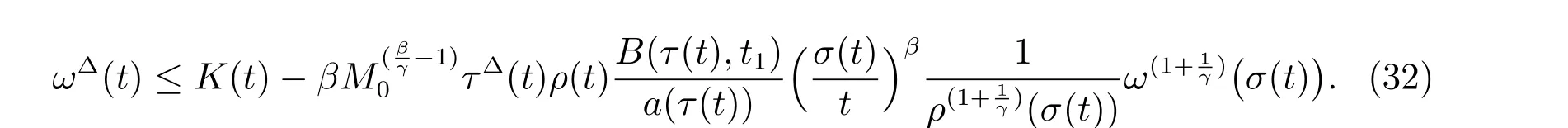
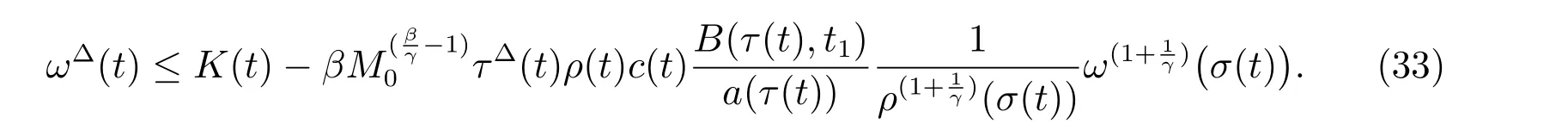
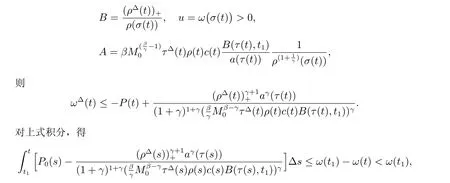


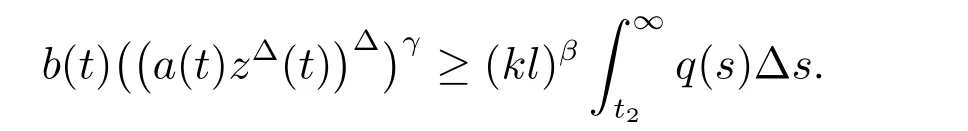

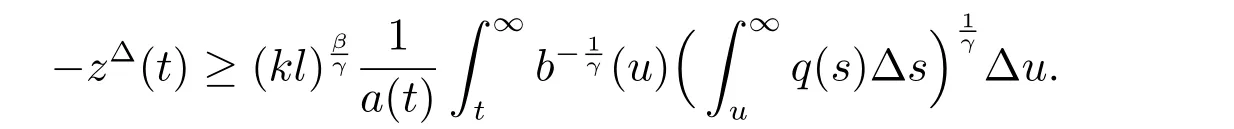
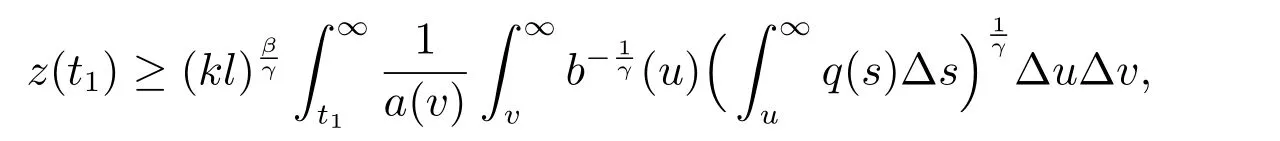
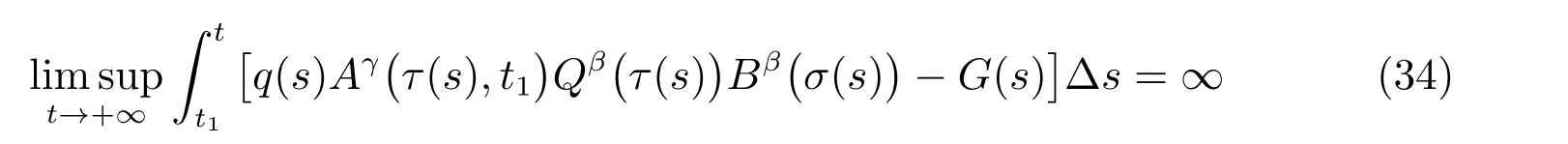



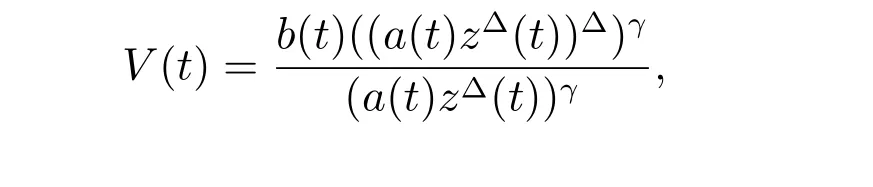
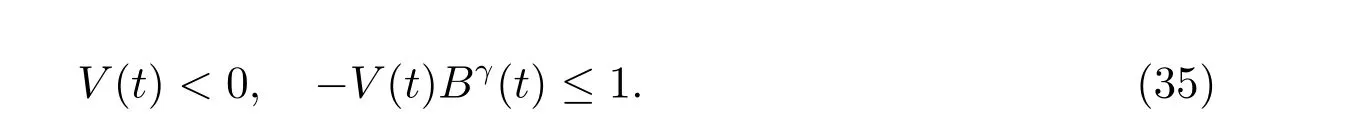
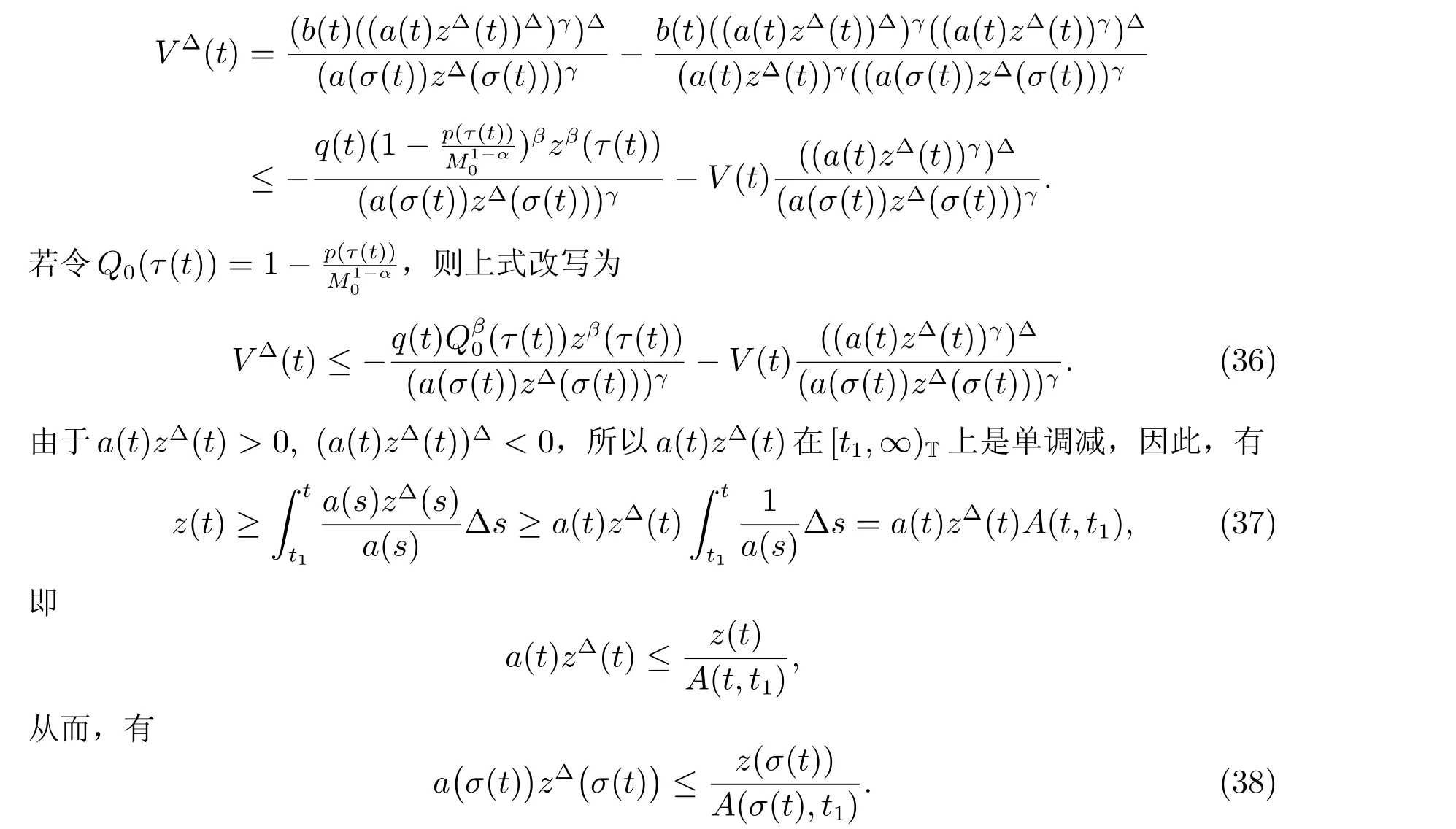
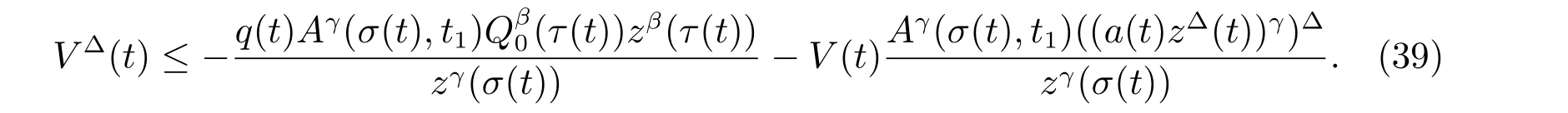

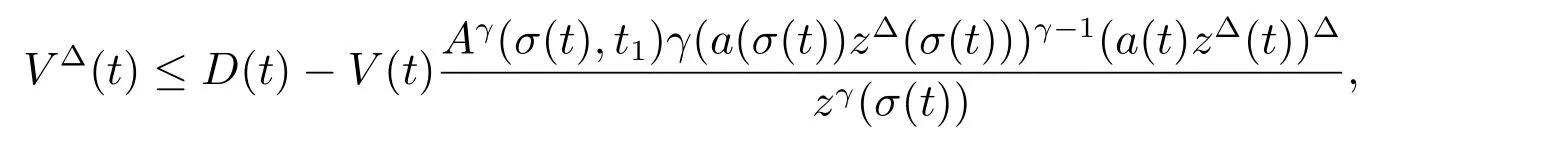

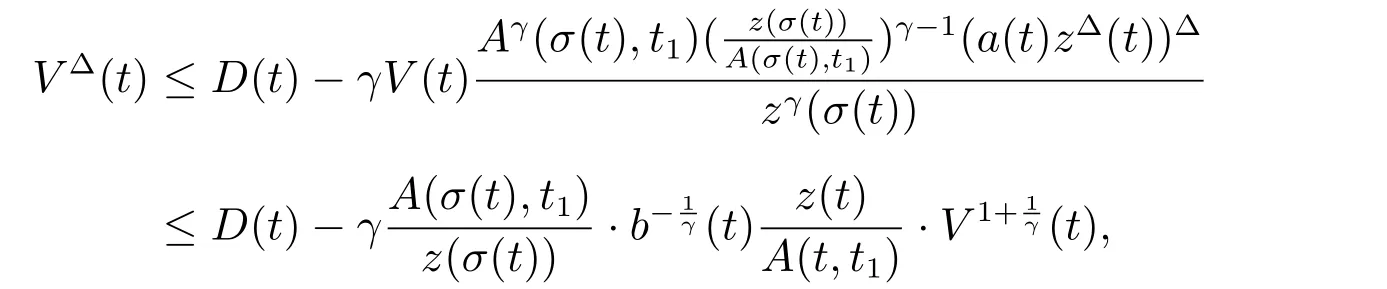
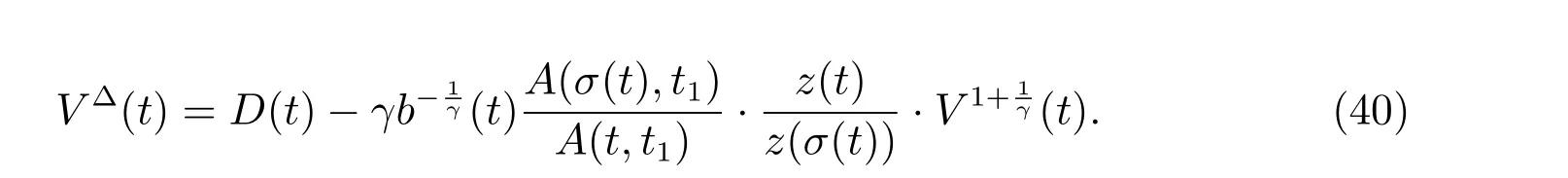
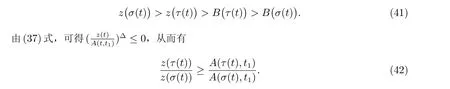
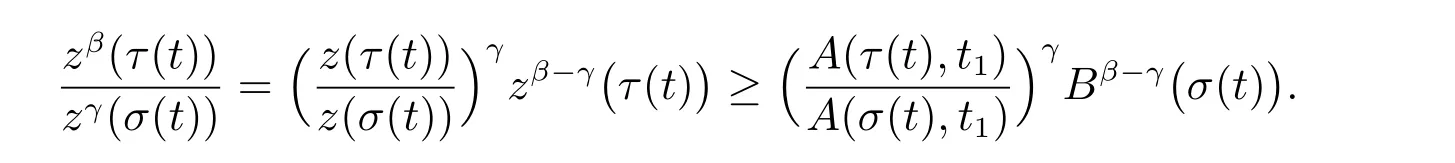
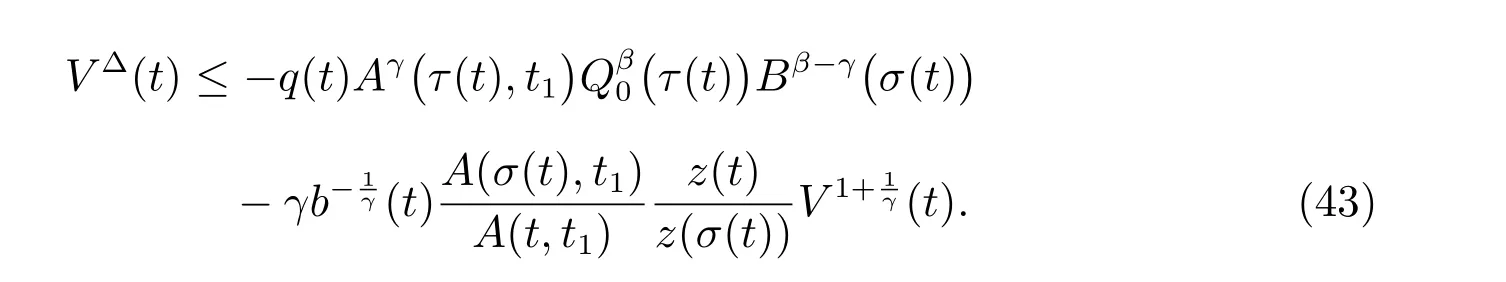

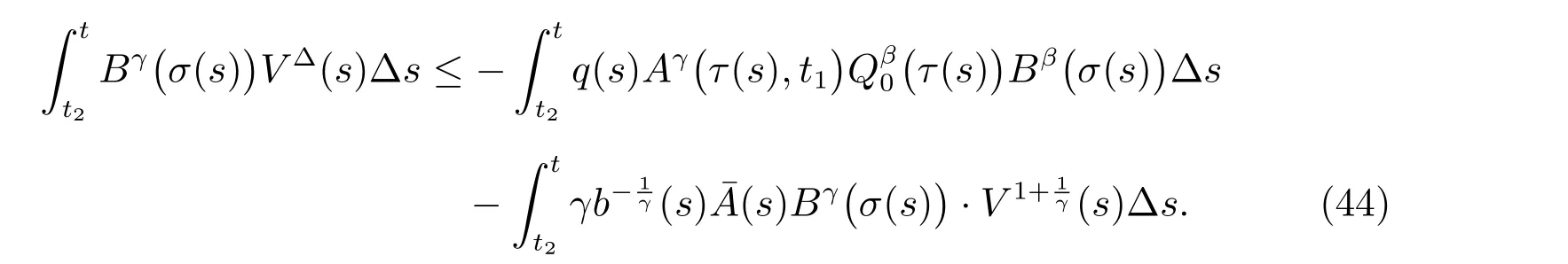

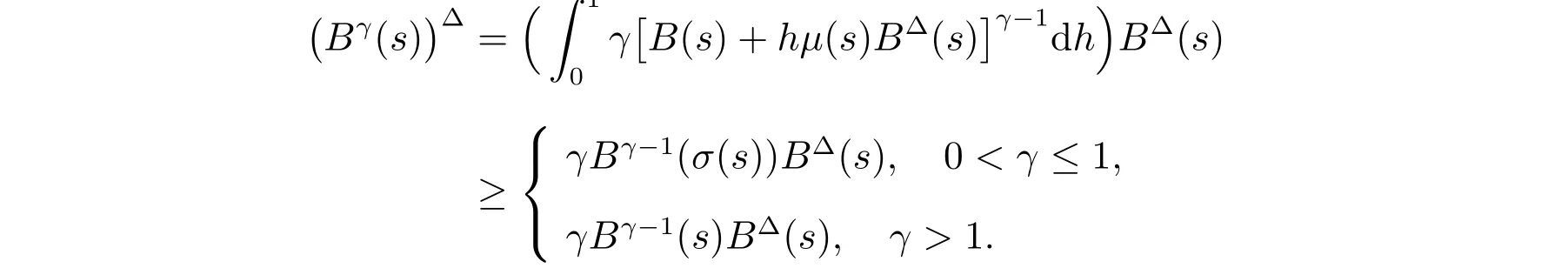
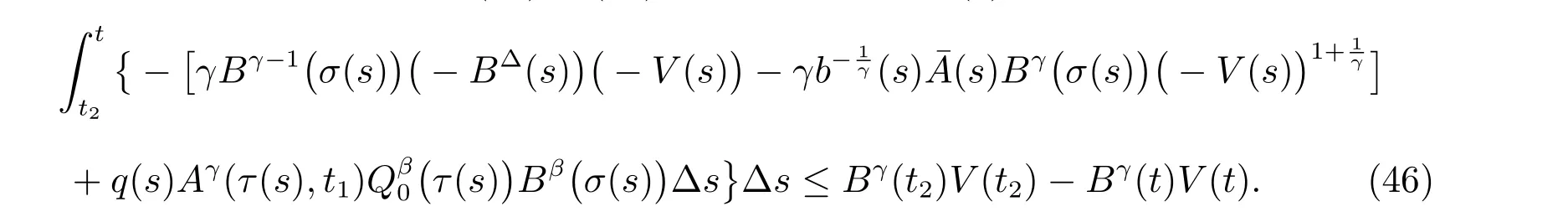
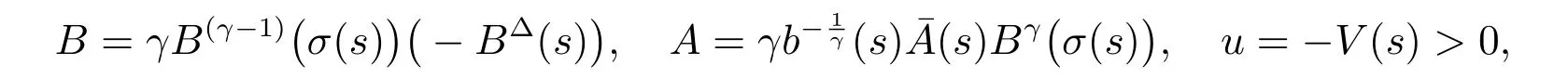
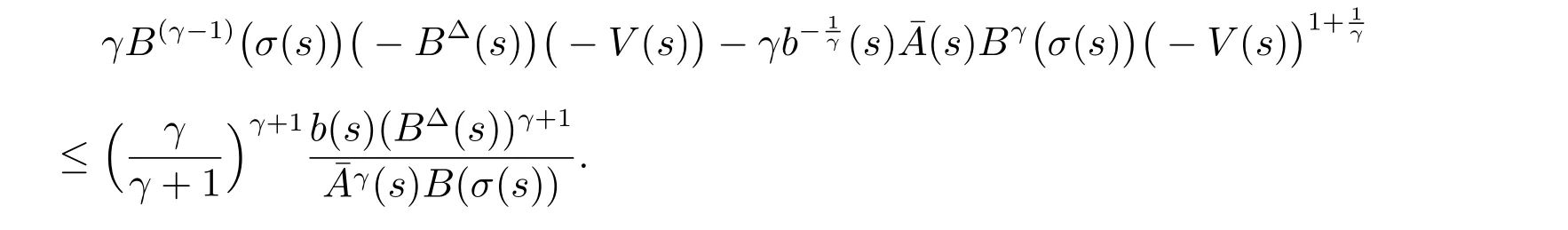

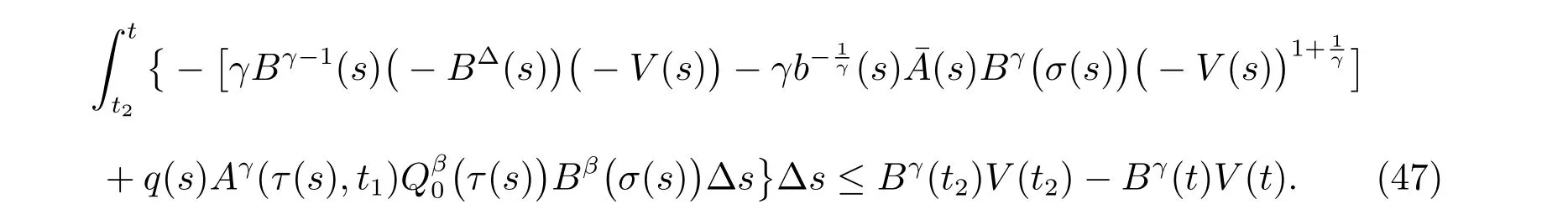

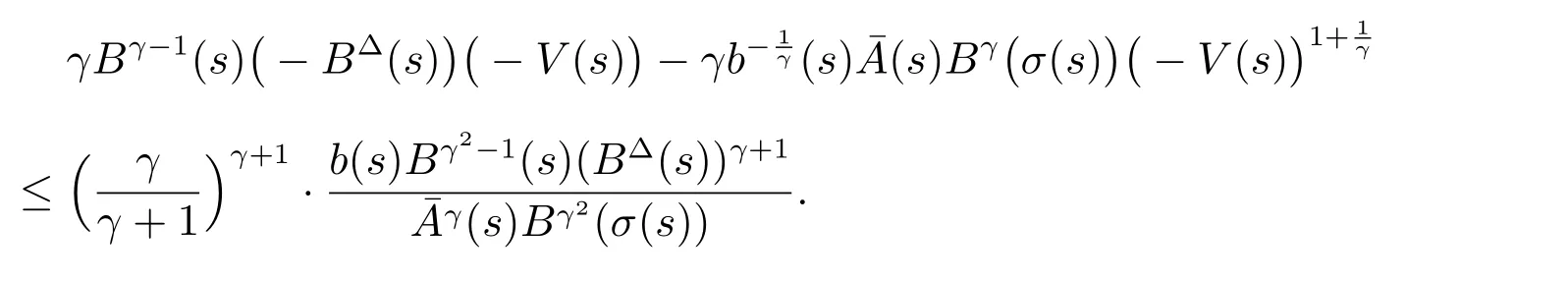
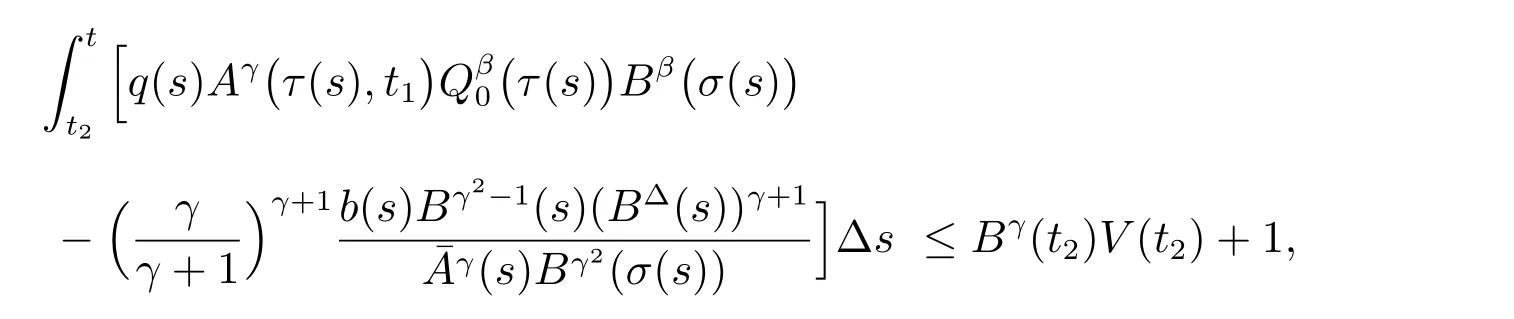
3 应用实例
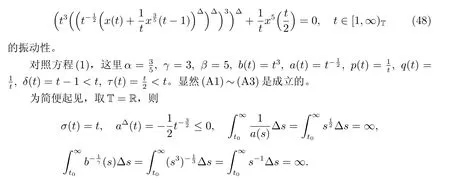


4 结论
