基于不变矩的书法真伪鉴定方法研究

姬 静

(1. 西安交通大学档案馆、博物馆，西安 710049;2. 西安交通大学机械制造系统工程国家重点实验室，西安 710049)

0 引言

我国是四大文明古国之一，五千年的文明为我们留下了丰富的文化遗产，其中书法作品更是历史悠久，源远流长，情况也最为复杂。为了能够更加深入的挖掘书法作品的艺术价值，为历史研究和书法收藏提供有效依据，书法作品的真伪鉴定显得尤为重要，它不仅是书法史以及书法艺术研究的重要课题之一，也是一直以来困扰书法作品收藏界的难题。

一直以来，书法作品的真伪鉴定问题都被归属于艺术领域。专家鉴定法依然是当前主流的书法真伪鉴定方法。其主要做法为：专家根据个人经验，从书法作品的艺术风格、时代风格、个人风格、书法内容、笔法、结构、章法以及题款、印章、材质等方面入手，进行综合判定[1]。由于伪作与真迹会存在局部上的细微差异，专家只能将作品的局部区域与真作一一比对，不要说一些巨幅作品，就是常见的书法作品，要将所有区域进行分别比对，可想而知其工作量是多么庞大，如此繁重工作反而更容易造成鉴定结果准确率的降低，因此，该方法不仅耗时耗力，而且准确率不高。另一方面，该方法主要依靠鉴定专家的个人主观因素，缺乏可以量化的，客观的鉴定指标，对于同一幅书法作品，不同的专家可能会给出截然相反的鉴定结果，容易引起争议。伴随着数字化、智能化时代的到来，国内外一些著名大学及研究机构，例如：澳大利亚昆士兰理工大学、新加坡管理大学、宾夕法尼亚州立大学、浙江大学、北京交通大学、中科院计算所等单位的研究学者已经在中国书法作品的自动分类、自动识别等领域开展了一些探索与研究[2–3]，这些研究使得书法鉴定专家进行书法分类、检索的时间得到了极大节省，可以将其精力及工作的重心放到书法真伪识别与鉴定上。另一方面，基于深度学习的图像识别技术是数字图像研究领域的一个重要分支与研究方向，并且在近几十年来得到了极大的发展，在人脸识别、条形码识别、交通信息化及计算机视觉等诸多领域，该技术均得以应用[4–5]。因此，本文也将基于深度学习的图像识别技术应用于书法真伪鉴定，从多个方面分析其结果并与本文所提出的方法进行比对。

目前常见的书法仿制手段有三种：高仿印刷、临摹和两者混搭。由于书法仿制手段的发展，即使是对相同版面、相同内容的两幅书法作品进行真伪鉴定，依靠人工及肉眼已很难识别，然而，真伪书法作品不可避免的存在形状上细微差异，尽管肉眼难以察觉。本文的研究主要针对上述问题，将模式识别领域中的不变矩应用于书法真伪鉴定，提出了形状真实度的概念，分析比较了七种常用不变矩的形状真实度性能，实验结果表明，由Hu 矩计算的形状真实度性能最佳，能够识别出肉眼不易观察的细节差异。能够为书法鉴定提供科学可靠的辅助手段，具有一定借鉴意义。

1 形状真实度

本文提出的形状真实度概念基于模式识别领域中的不变矩。目前常用的不变矩包括Hu 矩、Zernike 矩、Pseudo-Zernike 矩、Legendre 矩、Fourier-Mellin 矩、Tchebichef矩和Krawtchouk 矩。

1.1 Hu 矩

Hu 矩是一种经典的不变矩，在1962 年由Hu 提出[6]，具有平移、旋转和缩放不变性。对于图像f(x,y)，其p+q阶几何矩的定义为

p+q阶中心距的定义为

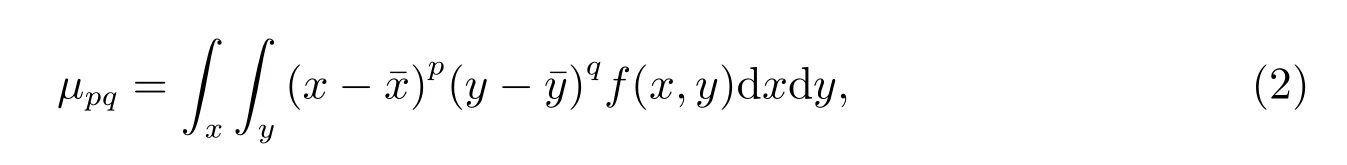
其中(¯x,¯y)为图像的重心坐标，满足

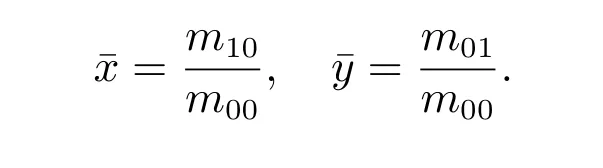
归一化的中心距定义为

Hu 根据归一化的中心距构造了7 个不变矩

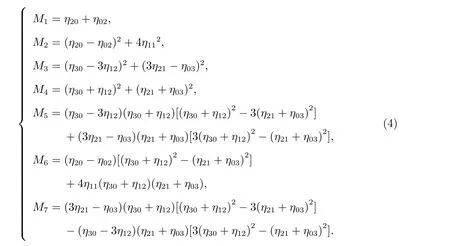
1.2 Zernike 矩

Zernike 矩是一种无信息冗余的连续正交矩，广泛应用于图像重建、目标识别、数字水印、边缘检测、图像检索等领域。对于图像f(x,y)，重复率为q的p阶Zernike 矩的定义为[7]

该式须满足条件(p −|q|)为非负偶数。式(5)中，f(ρ,θ)为图像f(x,y)的极坐标形式；(ρ,θ)为Zernike 多项式Vpq(ρ,θ)的共轭复数，Zernike 多项式的定义为

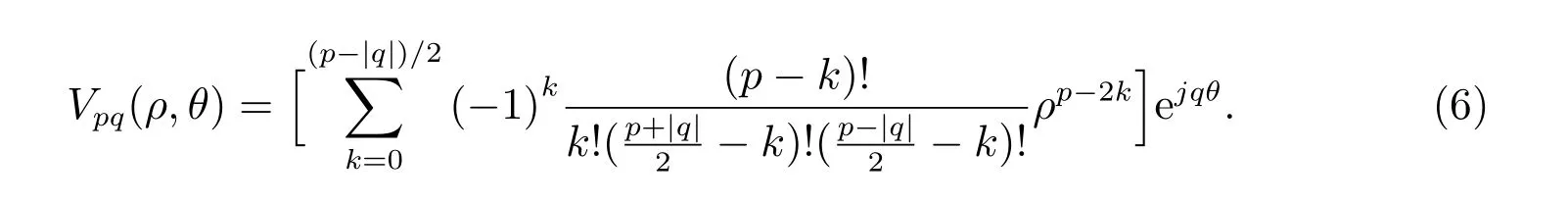
1.3 Pseudo-Zernike 矩

与Zernike 矩相比，Pseudo-Zernike 矩具有更好的特征表现性和噪声稳定性[8]。Pseu do-Zernike 矩的形式与Zernike 矩的形式相似，仅需将Zernike 多项式换为Pseudo-Zernike多项式。Pseudo-Zernike 多项式的定义为[9]

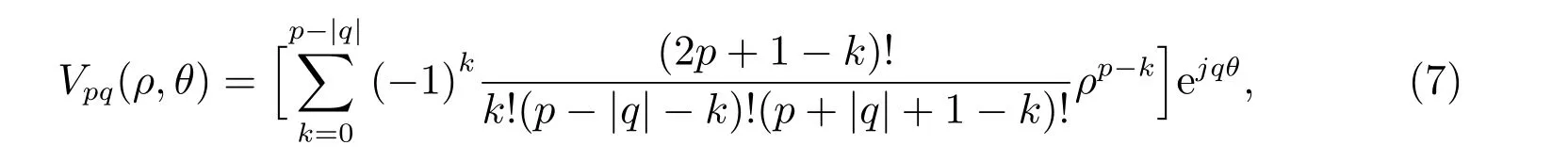
该式只需满足(p −|q|)为非负整数。

1.4 Legendre 矩

Legendre 矩也是一种使用广泛的连续正交矩，(p+q)阶Legendre 矩的定义为[10]

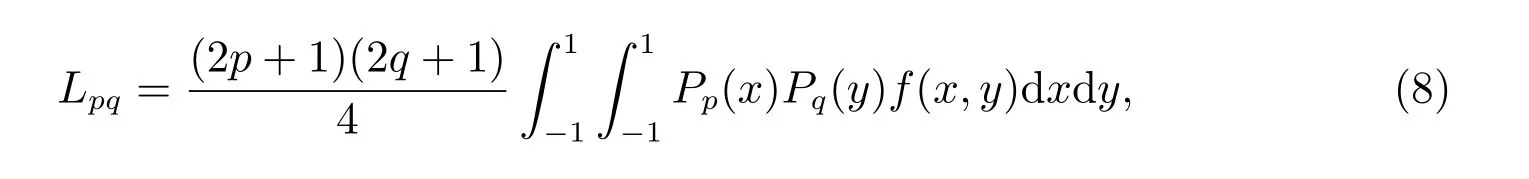
其中Pp(x)为p阶Legendre 多项式，其定义为

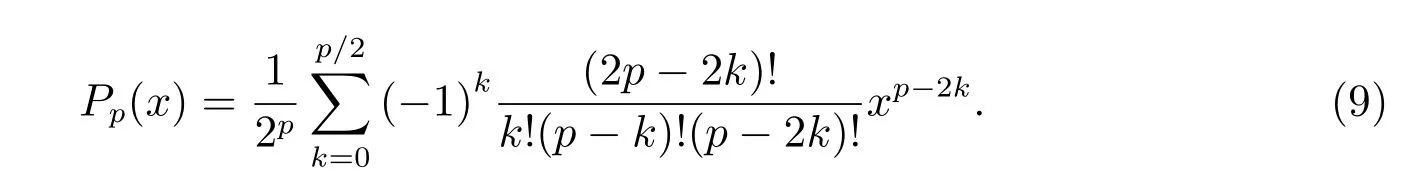
1.5 Fourier-Mellin 矩

正交Fourier-Mellin 矩是一种广泛应用于模式识别、边缘检测等领域的连续正交矩。对于图像f(x,y)，重复率为q的p阶Fourier-Mellin 矩的定义为[11]

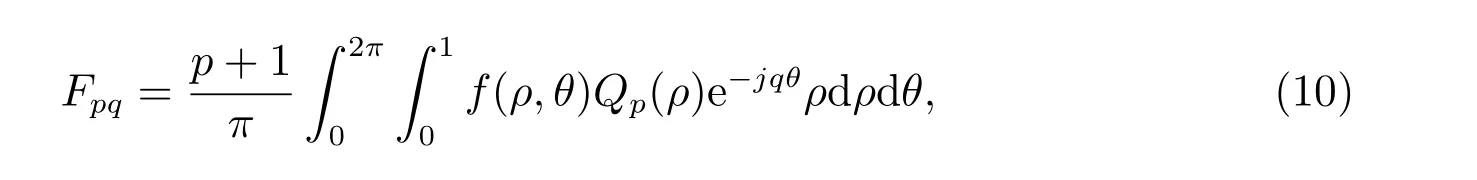
其中Qp(ρ)为ρ的p阶多项式，其定义为

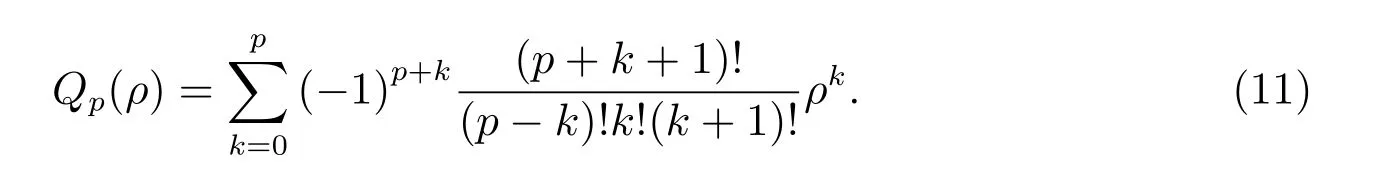
1.6 Tchebichef 矩

Tchebichef 矩是由Mukundan 等人[12]提出的离散正交矩。对于宽度为M、高度为N的图像f(x,y)，(p+q)阶Tchebichef 矩的定义为

该迭代关系的初始值为

˜ρ(p,M)的表达式为

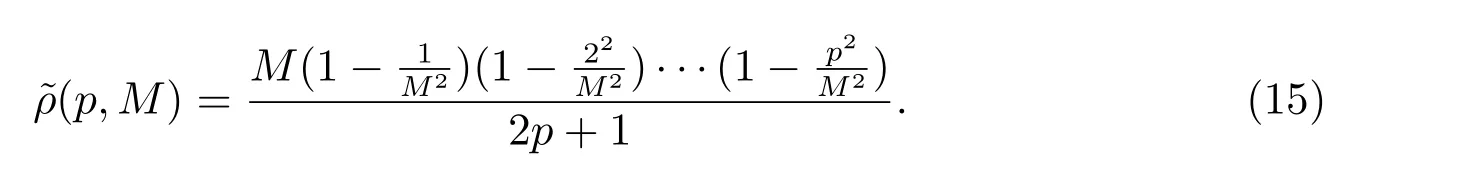
1.7 Krawtchouk 矩

Krawtchouk 矩是由Yap 等人[13]提出的离散正交矩，对于宽度为、高度为N的图像f(x,y)，(p+q)阶Krawtchouk 矩的定义为

该递推关系的初始值为

其中w(x;m,M −1)为加权函数，满足迭代关系

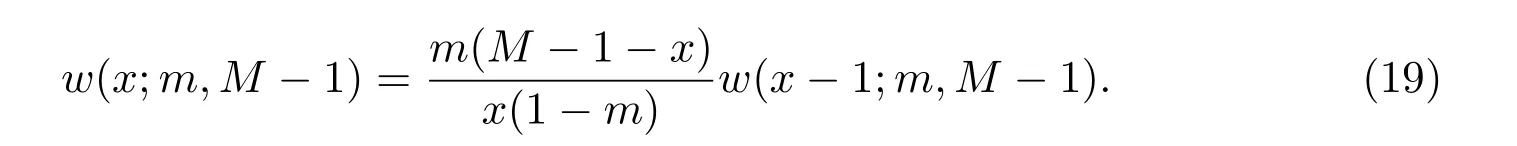
迭代关系的初始值为

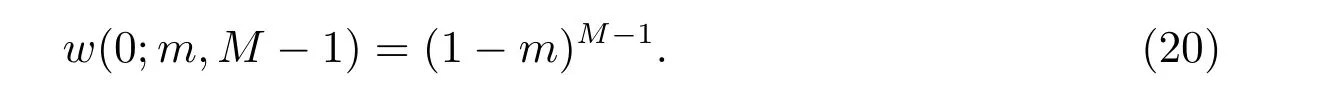
由于不变矩能够描述图像中物体的形状特征[15]，根据两幅图像之间不变矩的差异，定义图像A 中物体相对于图像B 中物体的形状真实度

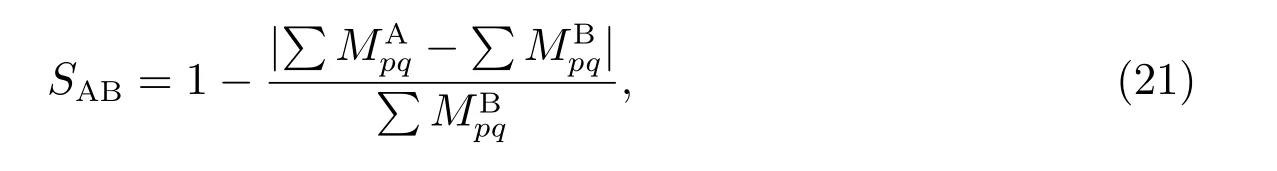
2 书法真伪鉴定方法

本文提出的书法真伪鉴定模型由硬件与软件两个系统构成，硬件装置由本项目组自行研发设计，是专门针对书法作品的高清数字化扫描设备，如图1 和图2 所示。该设备采用了两个对书法作品友好的，发光强度稳定且均匀的白色线型光源，该光源发出的光经过高精密的柱状透镜聚合后，照射到书法作品的同一扫描区域。线阵相机CCD 将该区域所成的像转化为电信号，经过图像采集卡量化处理后，形成数字图像并存储于计算机中，其实现了光信号到电信号再到数字图像的信号转换。

图1 书法作品高清数字扫描设备硬件装置图

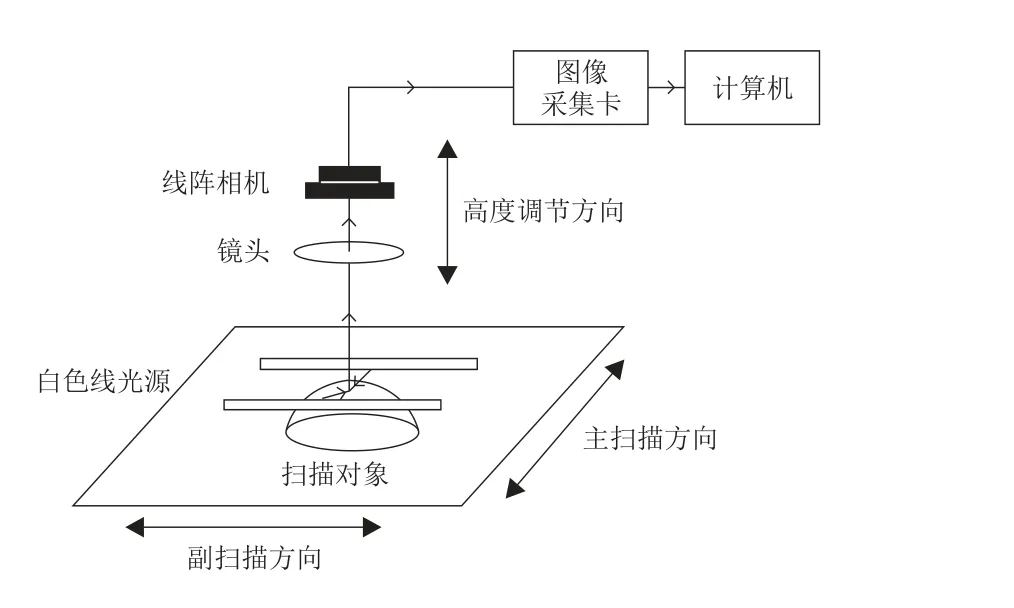
图2 书法作品高清数字扫描设备硬件原理图

由于本系统采用的是CCD 线阵相机，它一次只能采集一行扫描对象的高清晰图像。因此，为了获得一帧图像，光学系统(由光学镜头与线阵CCD 相机组成)需要沿着主扫描方向进行运动以实现对扫描对象的全部数据采集。软件系统的鉴定流程图如图3 所示。

图3 基于形状真实度的书法真伪鉴定方法的流程图

通过扫描设备获取待鉴定书法作品和目标书法作品的图像信息，首先对待鉴定书法作品的图像和目标书法作品的图像进行预处理。由于光学数码设备获取的图像含有镜头畸变，故在预处理过程中需要进行镜头畸变校正[16]。此外，还要消除其他因素如亮度、颜色的影响，本文采取了图像二值化的处理方式。但是我们所采集的书法作品往往年代久远，污渍、破损等情况不可避免，这些大大增加了预处理的困难和麻烦。这是因为污渍及破损区域，通过数字扫描表现在图像上，其灰度值与书法作品本身的文字的灰度值相差不大，使得二值化的效果大大降低。Otsu、Sauvola、Kittler、Niblack、自适应阈值[17–18]都是目前主流的二值化算法。其中，自适应阈值方法是通过灰度直方图来确定二值化阈值的方法。其确定的阈值和最终得到的灰度图像密切相关于不同灰度值图像的像素数目。具体说来，首先计算图像中不同灰度值所对应的像素总数，对书法作品而言，总体上讲基本是白底黑色，但是因为年代久远等因素的影响，存在纸张泛黄等现象，尽管如此，其灰度直方图仍然会存在两个较为明显的峰值，我们将两个峰值中间的最低点的灰度值作为二值化的阈值，大大提升了二值化的效果，这是由于该阈值使得灰度值较大的像素的数目与灰度值较小的像素的数目恰好同时达到最大，这样不仅最大程度地保持了书法笔划的细节特征，并且由于所扫描的文字源图像一般灰度值变化不大，比较平缓，这样的像素点就会统一被处理，在最终获得的二值化图像中，文字边缘不易产生毛刺等现象，作品的纹理特征会更好的呈现出来。综上，本文选取自适应阈值二值化方法。两幅图像经预处理后，计算待鉴定书法作品图像相对于目标书法作品图像的形状真实度，如果该值大于形状真实度的阈值，则判断待鉴定书法作品为真，反之则为假。书法形状真实度阈值的选取通常需要一定的经验，对于不同的书法作品应取不同的阈值，阈值的选取需要考虑平移、旋转和缩放变换对图像形状真实度的影响，具体方法见3.2 节。

3 形状真实度的性能分析

在进行书法真伪鉴定时，由于拍摄条件不可能完全相同，获取的待鉴定书法作品图像和目标书法作品图像之间会存在位置、角度和比例上的差异，即便经过图像变换处理也不能将这种差异完全消除，因此有必要对形状真实度的平移、旋转和缩放不变性进行分析。除此之外，还需讨论形状真实度对书法形状差异的识别能力，识别书法形状差异是实现书法真伪鉴定的依据。本研究分别针对形状真实度的平移、旋转和缩放不变性分析以及形状真实度对于书法差异的识别能力两方面设计了专门的软件系统，用于进行形状真实度的性能分析，以此说明本文所提出的图像形状真实度方法对于书法真伪鉴定的借鉴意义及实用价值。

3.1 平移、旋转和缩放不变性

理想的形状真实度应只与两幅图像的形状有关，而与图像的平移、旋转和缩放变换无关。但在实际应用中，由各矩计算的形状真实度并不具有理想的平移、旋转和缩放不变性。因此，需为形状真实度选取具有平移、旋转和缩放不变性的最佳矩。为测试各矩计算的形状真实度的不变性，设计了如图4 所示的程序框架结构，采用了如图5 所示的实验对象，图5(a)至图5(d)分别为永字行书、永字隶书、勤字行书、勤字隶书的图像。

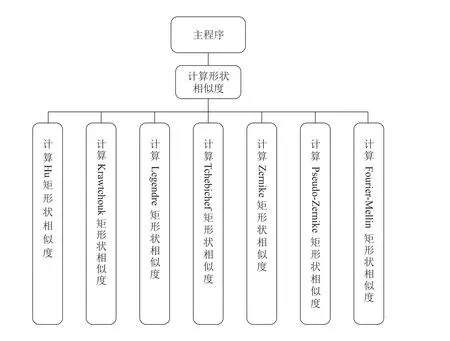
图4 形状相似度计算程序的结构框架

图5 形状真实度不变性测试的实验对象

实验中所有图像的尺寸均为1 000×1 000 像素，平移变换实验中采用的平移向量为(100,0)、(100,100)、(0,100)、(−100,100)、(−100,0)、(−100,100)、(0,−100)、(100,−100)，将这八组平移实验中的最小形状真实度作为衡量平移不变性的性能指标。在旋转和缩放变换实验中，考虑到实际进行书法鉴定时多为用同一数码设备获取的图像，实验采用了小角度旋转和小比例缩放，旋转的角度为±5◦和±10◦，缩放比例为0.9 倍、0.95 倍、1.05 倍和1.1 倍，将旋转和缩放实验中的最小形状真实度作为衡量旋转不变性和缩放不变性的性能指标。

此外，实验还计算了平移、旋转和缩放变换的综合不变性

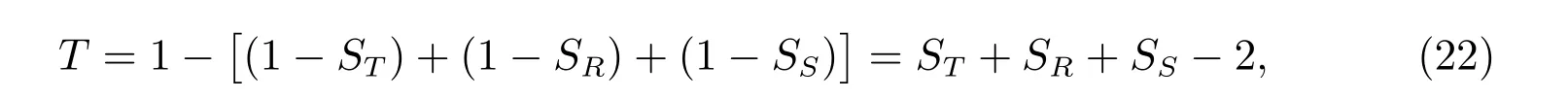
其中ST、SR和SS分别为真品书法图像在平移、旋转和缩放中的最小形状真实度。将三种变换的形状真实度差异累加，即是图像变换中的最大差异，据此可计算出图像在复合变换中的最小形状真实度，以此作为综合不变性的性能指标。综合不变性越趋近于100%，说明平移、旋转和缩放不变性越好。实验中各矩的综合不变性如表1 所示，表中Zer 矩代表Zernike 矩，Pse 矩代表Pseudo-Zernike 矩，Leg 矩代表Legendre 矩，Fou 矩代表Fourier-Mellin 矩，Tch 矩代表Tchebichef 矩，Kra 矩代表Krawtchouk 矩。从表1 可以看出，由Hu 矩计算的形状真实度在各组实验中的综合不变性均能达到99%以上，高于其他矩计算的形状真实度。这意味着由Hu 计算的形状真实度具有最佳的平移、旋转和缩放不变性。因此，Hu 矩是描述形状真实度的最佳矩。

表1 由各不变矩计算的形状真实度的不变性比较

3.2 书法形状差异的识别能力

为测试形状真实度对书法形状差异的识别能力，采用图6 所示的书法对本文提出的形状真实度进行测试。

图6 书法形状差异的识别能力测试对象

从图6 可以看出，真品书法作品与赝品书法作品之间差别很小，不易用肉眼辨别。实验中分别将真品《清静无为》书法作品、赝品《清静无为》书法作品、真品《诫子书》书法作品和赝品《诫子书》书法作品作为待鉴定书法作品，计算待鉴定书法作品图像相对于真品书法作品图像的形状真实度，以及由式(22)计算的平移、旋转和缩放综合不变性，结果如表2 所示。由式(22)计算的综合不变性反映了图像平移、旋转和缩放过程中的最小形状真实度，可将该值作为识别书法形状差异的阈值。当待鉴定书法作品图像相对于目标书法作品图像的形状真实度大于该值时，判断待鉴定书法作品为真；否则，则判断待鉴定书法作品为假。从表2 可以看出，真品《清静无为》书法作品的形状真实度大于综合不变性阈值，鉴定结果为真品；赝品《清静无为》书法作品的形状真实度小于综合不变性阈值，鉴定结果为赝品；真品《诫子书》书法作品的形状真实度大于综合不变性阈值，鉴定结果为真品；赝品《诫子书》书法作品的形状真实度小于综合不变性阈值，鉴定结果为赝品；以上实验结果与实际情况一致。

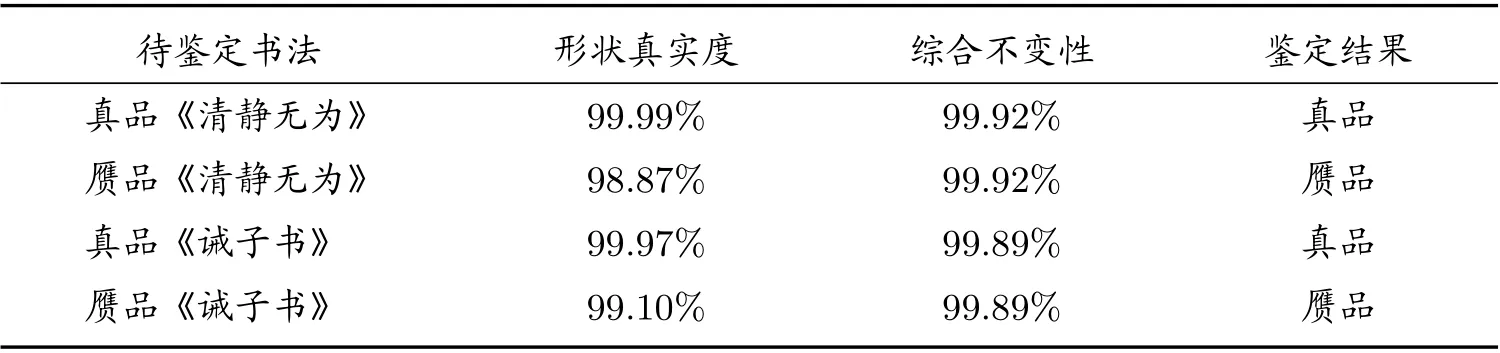
表2 书法形状差异的识别能力的测试结果

进一步，为了验证系统的鉴别能力和系统性能，在测试系统的过程中，我们针对包含真伪的184 幅书法作品，分别使用了专家鉴定法，基于深度学习技术的鉴定方法以及本文提出的方法进行测试比较，在实验中采用的是交叉验证的方法，即：将184 幅样本中的183 幅作为训练集，建立模型，剩余1 幅作为测试集，检验模型。如此分别轮换测试集和训练集，完成对所有样本的训练与检验，测试结果如下。

1) 鉴定准确率

2) 鉴定时间开销

为了说明鉴定系统的效率，我们在上述实验中测试了三种方法的时间开销。测试结果见表4，从表4 中可以看出，本文所提出的方法的平均鉴定时间开销为15.17 ms，与其他两种方法相比，鉴定效率最高，具有明显优势。

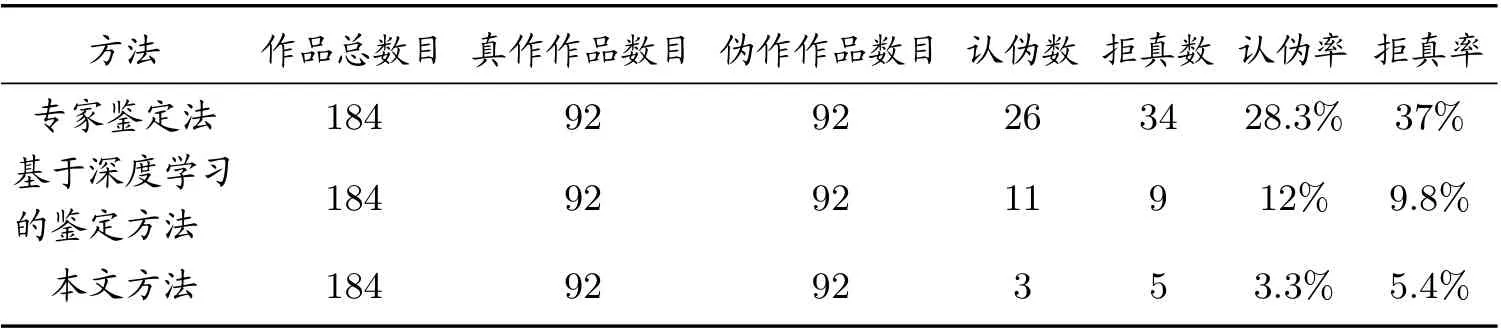
表3 书法作品鉴定准确率验证结果

表4 书法作品鉴定效率验证结果

3) 抗干扰性

为了进一步验证三种方法在鉴定过程中的抗干扰性能，我们对上述测试样本分别添加了随机噪声，使用以上三种方法鉴定真伪，以此来验证并对比三种方法的抗干扰性能。结果如表5 所示，可以看出，本文方法鉴定准确率略有降低，但是影响不大，仍是可接受范围。需要注意的是，由于不变矩不具有理想的平移、旋转和缩放不变性，当一幅赝品书法作品的形状无限接近于真品书法作品时，会存在形状真实度无法区分两幅书法作品形状差异的情况。尽管如此，由Hu 矩计算的形状真实度仍可以识别出肉眼不易观察的书法作品细节差异，具有较好的实用价值。

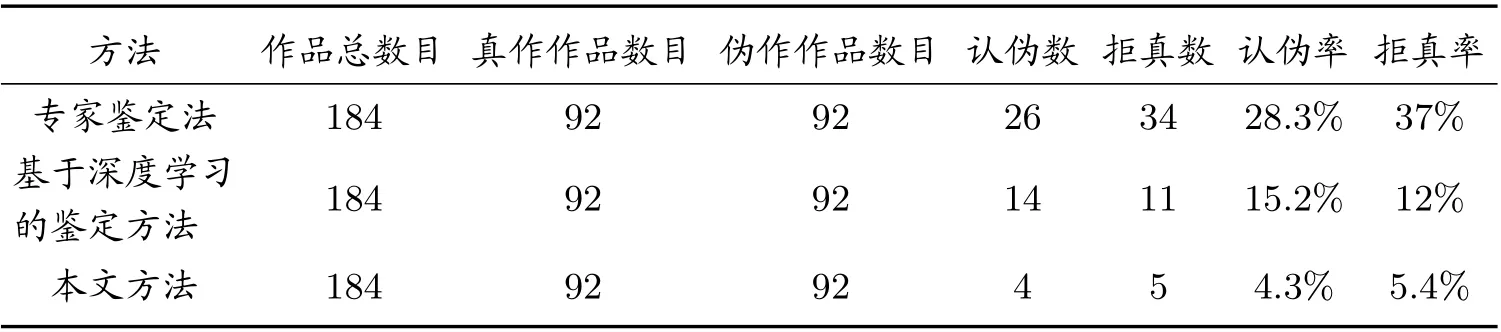
表5 书法作品鉴定抗干扰性能验证结果

4 结论与展望

本文将模式识别领域中的不变矩应用于书法作品真伪鉴定，提出了形状真实度的概念，用该指标衡量待鉴定书法作品图像相对于真品书法作品图像的形状真实程度，通过设定阈值的方法对书法作品的真伪进行鉴定。文中分析比较了Hu 矩、Zernike 矩、Pseudo-Zernike 矩、Legendre 矩、Fourier-Mellin 矩、Tchebichef 矩和Krawtchouk 矩等七种常见不变矩的形状真实度的性能。实验结果表明，Hu 矩是描述形状真实度的最佳矩，并且该系统通过高清晰、高精度、高保真的书法作品的图像采集与处理，进一步保证了鉴定的可靠性，由于不可避免的存在噪声等因素的影响，系统的确存在误判，但是误判率较低，且该系统能够识别出肉眼不易观察的细节差异。通过与主流的专家鉴定方法相比：是鉴定书法作品真伪的辅助依据，可以提高书法作品鉴定的效率与可信性，与基于深度学习的真伪识别方法对比，该方法的鉴定准确率高，鉴定时间开销短，且抗干扰性好。在书法真伪鉴定中具有较好的实用价值。本文将模式识别领域与书法作品真伪鉴定的结合与应用做了一些探讨和尝试，实验证明该方法的可行性，后续可考虑由近及远，对当代及近现代的书法作品，采用高精度的数字化扫描及拍摄手段，建立书法作品数字化数据库，通过本文提出的方法，可对库中的书法特征进行对比与匹配，从而为专家鉴定书法提供一种科学可靠的辅助手段，具有一定借鉴意义。进一步地，应用本文的方法如何解决同一书法风格不同书法作品的真伪鉴定问题，以及书法风格随着年龄而逐渐变化的书法作品的真伪鉴定问题，有待后续下一步的研究与拓展。