活塞内冷油腔中纳米流体振荡流动与传热特性影响因素研究
2022-07-06邓晰文谢光义王金昆雷基林朱蕊东
肖 杰,邓晰文,,谢光义,王金昆,雷基林,,朱蕊东
(1.昆明理工大学云南省内燃机重点实验室,昆明 650500;2.昆明云内动力股份有限公司云南省内燃机高原排放重点实验室,昆明 650200)
0 概述
随着内燃机强化程度的进一步提高,活塞在气缸内承受着更高的热负荷。缸内超过50% 以上的热流传递到了活塞上[1],活塞若得不到有效的冷却,将影响内燃机的整体耐久性及可靠性。内冷油腔振荡冷却是一种有效的活塞冷却方式,冷却油从喷油嘴喷入冷却通道,随着活塞的往复运动,冷却油对高温壁面产生冲击作用,从而显著降低活塞的热负荷。此外,冷却介质的设计也在一定程度上影响着活塞的冷却性能。
1995年文献[2]中提出了纳米流体的概念。由于纳米流体具有良好的悬浮稳定性,应用到内燃机冷却系统中不会出现纳米颗粒沉积、冷却通道堵塞的现象,且纳米流体的导热系数比机油大很多,大量的研究结果表明,纳米流体应用到众多工程领域都展现出了优异的传热性能[3-4]。文献[5-6]中研究了纳米流体对发动机传热摩擦性能的影响,表明加入纳米颗粒可减少发动机机械损失,显著提高换热能力。文献[7]中研究了不同体积分数下Cu 纳米机油和金刚石纳米机油的流动与换热特性,结果表明纳米流体能显著提升油腔的换热能力。文献[8-10]中采用了流体体积(volume of fluid,VOF)方法与Leverl-Set 方法耦合的方式研究了不同体积分数的金刚石纳米颗粒对油腔的瞬态传热影响,结果表明随着体积分数的增加,油腔的换热能力增强。此外还有大量研究表明纳米流体的换热性能明显优于传统工质[11-13]。但以往纳米流体强化内冷油腔传热增强的数值模拟中,并没有详细地探讨纳米流体传热增强的机理。
为了深入研究纳米流体强化传热的规律,本文中采用Fluent 和CFX 软件及相对位移方法[14]建立了纳米流体的振荡传热数值仿真模型,引入了不同种类(Al2O3、CuO、SiO2纳米机油)和不同体积分数的纳米流体的振荡流动特性,进一步研究了纳米流体振荡流动强化换热的机理,为强化活塞冷却提供了一定的理论支撑。
1 内冷油腔的振荡传热理论
在内冷油腔跟随活塞振荡的过程中,冷却油并没有完全充满内冷油腔,气相作为冷却油腔中的另一物理相,使得冷却油腔内部的机油流动呈现为复杂的“摇鸡尾酒”式液体绕壁面运动。冷却机油、空气与内冷油腔壁面之间的传热是周期性瞬态传热、周向对流换热等过程的综合[15]。在建立数值仿真模型时需要合理地简化物理过程,本文中参考文献[15-16]中的简化处理及以下假设来建立计算流体力学模型:(1)假设油腔内部的空气为理想气体;(2)假设纳米颗粒均匀地分散在机油中;(3)假设机油在油腔换热过程中不会蒸发,机油在振荡流动中不可压缩;(4)液相与气相互不相溶,不考虑能量交换。
机油在油腔内振荡的过程中与空气不相溶,存在明显的相界面,各相有独立的速度场和湍流场。采用欧拉-欧拉方法中多相流非均值流体的自由表面模型来模拟油腔振荡过程中气液两相流的流动状态。
在活塞往复运动的过程中,油腔内部的气液两相流形成了一种湍流流动。因此在仿真模拟过程中引入了湍流运输方程,选用的是k-epsilon(k-ε)湍流模型,采用 Scalable 壁面函数(Scalable wall function)处理近壁面网格,以提高模拟精度并加快模型的收敛。k-ε模型的湍流动能和耗散率方程分别用式(1)及式(2)表示。
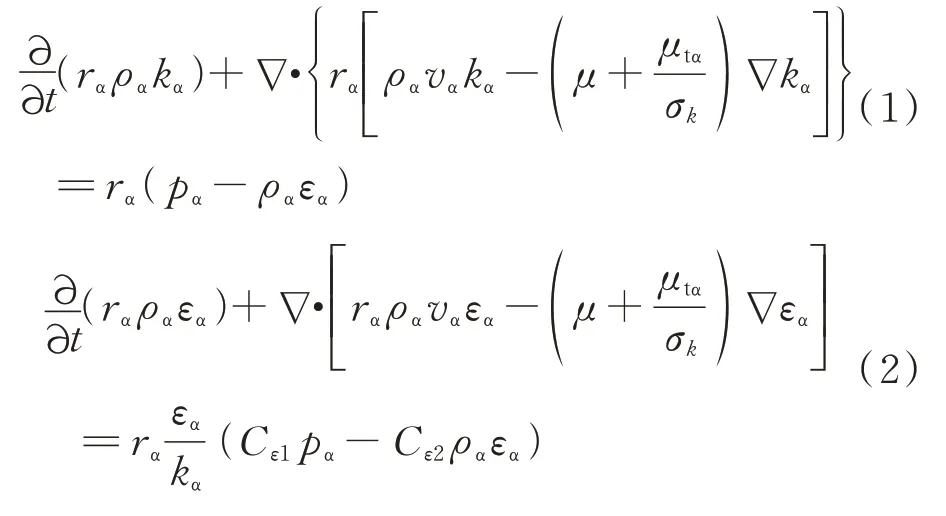
式中,rα为油腔内气相的体积分数;ρα为气相的密度,kg/m3;kα为气相湍动能;vα为气相速度,m/s;μtα为气相湍流黏度,g/(m·s);σk为湍流模型常数,取值1.0;εα为气相耗散率,m2/s3;Cε1和Cε2为k-ε湍流模型常数,分别取值1.44 和1.92;pα为气相压力,Pa;μ为动态黏度,g/(m·s);∇为哈密尔顿算子。
由于不考虑两相之间的能量传递,因此两相之间的相互作用几乎均由两相之间的速度差引起,使用式(3)所示的欧拉多相流动量传输方程来求解因速度差引起的动量。

式中,vβ为液相速度,m/s,[vα]为气相速度矩阵;μα为气相的动态黏度,g/(m·s);cαβ为气相与液相间的阻力系数。
液相与气相的能量方程由式(4)表示,使用式(5)和式(6)分别计算能量和温度。

式中,ke为有效导热系数,W/(m·K);v为速度,m/s;ρ为密度,kg/m3;E为空气相和机油相的平均能量,J;T为温度,K;r为体积分数;下标α、β 分别代表气相和液相。
2 数值仿真模型的建立
2.1 研究对象
以某柴油机活塞内冷油腔为研究对象,研究了不同纳米机油对油腔换热能力的影响。该柴油机的相关参数如表1 所示。

表1 发动机性能结构参数
2.2 几何模型
在发动机工作过程中,冷却油被喷油嘴喷入冷却油腔,与同时被卷吸进入油腔内的空气形成两相流,跟随活塞一起往复运动,在油腔内振荡与壁面进行热交换,从而冷却活塞。在计算流体力学模拟中使用完整的三维模型来模拟冷却通道。油腔为环形油腔,油腔的进出油道被简化为2 个圆柱体且进出油道的长度相同,喷油嘴位于进油通道的下方,进出油通道的长度为喷嘴位置到内冷油腔的距离,如图1所示。
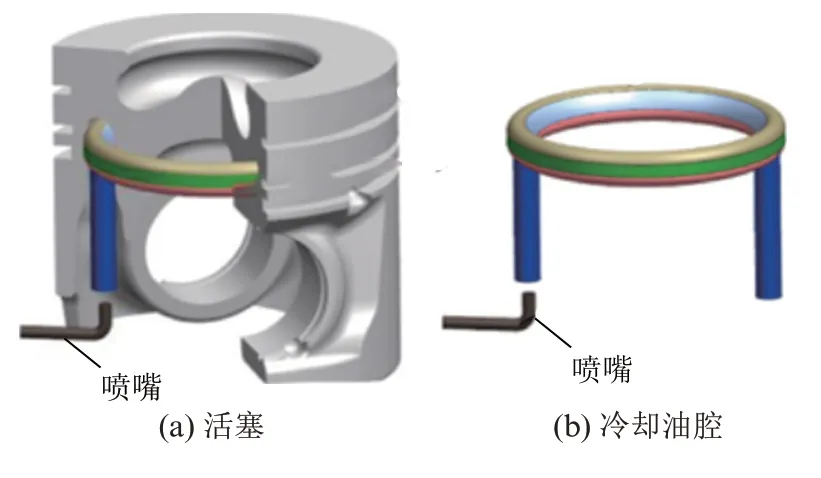
图1 活塞内部冷却油腔的布局和油腔的几何形状
2.3 边界条件及初始条件
活塞内冷油腔的振荡流动与传热是一个复杂的气液两相流过程。为了提高计算精度和减少计算量,要选用适当简化网格模型及合理设置边界条件和初始条件。本文中采用相对位移法[14],将原有的机油喷射等恒定边界条件转换为随活塞运动而变化的条件,始终保持内冷油腔与喷油嘴之间的相对位移为0,内冷油腔的机油入口速度可计算为当前喷嘴射流速度与活塞瞬时速度的差值。活塞瞬时位移和速度可用式(7)和式(8)表示。
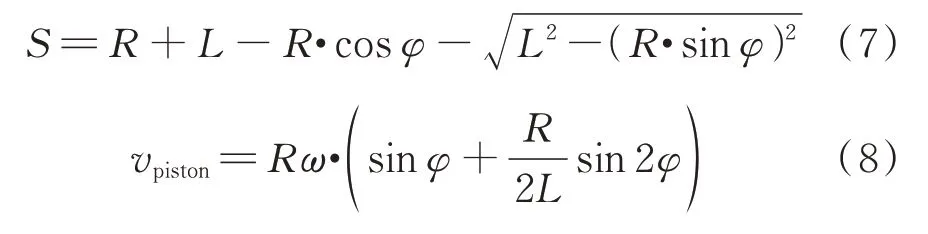
式中,S为活塞的瞬时位移,m;R为曲柄半径,m;L为连杆长度,m;φ为曲轴转角,rad;ω为曲轴的角速度,rad/s;vpiston为活塞瞬时速度,m/s。
机油射流速度主要受机油压力和机油密度的影响,如式(9)所示。根据机油的射流速度和活塞瞬时速度可以求出机油的入口相对速度,如式(10)所示。

式中,voil为喷油嘴出口处机油速度,m/s;η为流量损失系数,设定为0.08;poil为喷油嘴机油压力,Pa;ρoil为机油密度,kg/m3;vinlet为机油的入口相对速度。
以油的相对速度作为进油通道的边界条件,空气入口设定为开放边界条件,将环境大气压作为出口边界条件,油腔壁面与流体之间无滑移,油腔顶部、底部、内部和外部壁面温度以活塞温度场中提取的平均温度作为热边界条件,分别为534 K、473 K、503 K 和493 K。初始时刻求解域内的压强为静态压强,相对压力为0 Pa;气相和液相初始速度为0 m/s;由于初始时刻油腔内全部充满了空气,因此气相初始体积分数为100%,液相初始体积分数为0。
2.4 求解器的设置
在模拟内冷油腔振荡流动的瞬态模型时,采用二阶向后欧拉时间推进积分模式,设置的最大瞬态时间步为20°曲轴转角。由于在流体计算中时间步的长短对流体计算结果的收敛速度和计算速度有很大影响,因此本文中模拟内冷油腔的流动模型设置的计算时间步为0.5°曲轴转角,计算的时长为10 个工作循环,达到稳定条件后,选择最后一个工作循环进行机油速度、机油充油率、瞬态机油分布、传热系数的分析。
2.5 网格无关性验证
为了验证仿真结果不受网格数量的影响,对不同网格数量的内冷油腔模型进行仿真分析。建立网格单元数分别为39 099、49 595、64 483 的油腔模型A、B、C。使用普通机油作为冷却介质,模拟了发动机转速1 000 r/min 时油腔壁面的传热系数,如图2所示。B 模型相对于A 模型的传热系数最大变化率为4.72%,平均变化率为2.41%;C 模型相对于A模型的传热系数最大变化率为4.22%,平均变化率为2.23%[17]。研究发现,瞬态传热系数在不同曲轴转角下结果的变化均不超过5%[18-19],即可认为网格数量对计算的结果无关,所以本文选择网格数量为49 595 进行模拟研究。

图2 网格无关性验证
2.6 仿真模型的验证
为了验证仿真模型的准确性,进行了内冷油腔振荡流动的可视化试验。由于内冷油腔结构形状较复杂,很难准确地捕捉到机油的流动状态,因此将内冷油腔设计为矩形透明的空腔模型,如图3 所示。考虑到机油的黏度较高且透光性差,在试验和仿真中使用去离子水替代机油作为振荡流动介质。

图3 矩形透明的空腔模型
矩形透明空腔在上下往复振荡流动的可视化试验中,试验电机的转速为180 r/min,同时仿真模型的转速与试验电机转速保持一致。矩形透明空腔内的充液率为30%。图4 为空腔内两相流振荡流动的试验结果和仿真结果。从图中可以看出当活塞从上止点0°曲轴转角到下止点180°曲轴转角加速运动时,油腔内气液两相流呈现湍流状态,运动剧烈,产生大量的气泡,且液体可以覆盖油腔上顶面的一部分,在曲轴转角到达180°时大量液体到达下壁面;活塞换行后,受惯性力影响,在曲轴转角为270°时大量机油还聚集在方腔底部,之后加速上行冲击方腔顶面到达上止点,从而完成一个循环。

图4 矩形腔内气液两相流的流型
为了验证传热模型的准确性,参照文献建立了仿真模型W、W1、W2[15,20-22]与本文中的仿真模型进行对比验证。其中仿真模型W 为完整的油腔模型,仿真模型W1 简化了油腔下方的空气域,仿真模型W2 简化了油腔进出口通道。4 个模型在相同的条件下进行计算,转速设为219 r/min,冷却介质用水代替机油,提取了油腔平均的充液率和壁面的综合传热系数,与文献[8]中的试验数据进行对比分析。该试验使用封闭的立方体空腔,通过热电偶方式获得了不同充液率下的传热系数如图5 所示。由图5可以看出仿真模型W 与本文中模型的结果更接近试验值。仿真模型W、W1、W2 的计算误差分别为-2.6%、12.8%、13.2%,本文中仿真模型计算误差为7.6%,但是本文中的仿真模型相比其他仿真模型不需要进行网格重构,节约大量时间的同时依然有较高的精度。
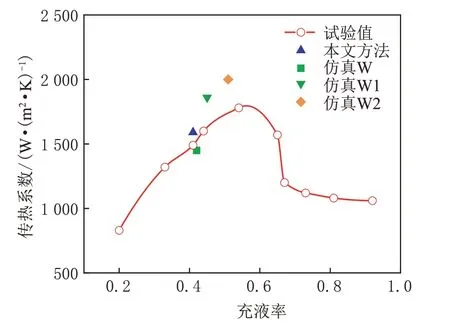
图5 不同仿真方法与试验结果对比
3 纳米流体的类型和热物性
本文中用机油作为传统介质,选择常见的3 种纳米颗粒[23-24],如表2 所示。

表2 纳米颗粒的物性参数
密度模型、比热模型、黏度模型和导热系数模型分别如式(11)~式(14)所示。以此热物性模型[25-26]计算出3 种纳米流体在不同纳米颗粒体积分数下的热物性参数,如表3 所示。

表3 机油的物性参数
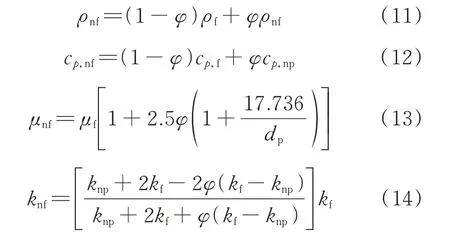
式中,下标np、nf、f 分别表示纳米颗粒、纳米流体、基础流体;ρ为密度,kg/m3;cp为比定压热容,J/(kg·K);u为黏度,g/(m·s);k为导热系数,W/(m·K);dp为纳米颗粒的直径,nm;φ为纳米颗粒的体积分数,%。
4 研究的结果及分析
为了研究纳米流体对内冷油腔换热性能的影响,通过比较纳米流体和普通机油在不同曲轴转角下的流动规律和对流换热特性,来深入探讨纳米流体强化内冷油腔传热的机理。
4.1 油腔内机油流动的规律
4.1.1 机油速度的分析
当发动机在标定转速时,油腔内机油的运动速度如图6 所示。设定为活塞从上止点到下止点的方向为机油速度的负方向,从下止点到上止点为机油速度的正方向。在传统机油内加入纳米颗粒使机油的密度增大,造成较大的惯性力。研究发现,在活塞从上止点到下止点运动过程中,曲轴转角在达到60°之前,机油的速度从小到大依次为CuO 纳米机油、Al2O3纳米机油、SiO2纳米机油、传统机油;机油加速向下止点运动过程中,在曲轴转角达到120°时,传统机油和纳米机油的速度规律相反,从小到大依次为传统机油、SiO2纳米机油、Al2O3纳米机油、CuO 纳米机油。综上可以看出,纳米机油的加速度比传统机油大。在机油快撞击到下壁面时开始减速,此时油腔内机油的速度从小到大依次为传统机油、SiO2纳米机油、Al2O3纳米机油、CuO 纳米机油。在活塞从下止点向上止点运动的过程中,变化规律相同,受惯性力影响,大量机油聚集在油腔底部,在机油开始向上止点运动过程中,惯性力较大的机油在起动时刻速度较小,在机油快撞击到上壁面时机油速度从小到大依次为传统机油、SiO2纳米机油、Al2O3纳米机油、CuO 纳米机油,从而完成一个工作循环。综上所述,在活塞往复运动的过程中,密度较大的纳米机油惯性力大,加速度大,在机油开始起动向下壁面撞击或者向上壁面撞击时速度较小,但在快到达上下壁面时速度较大,从而对壁面的冲击作用力更强烈,强化了内冷油腔的传热。

图6 不同曲轴转角下机油的流速
4.1.2 机油出口流量的分析
不同机油出口流量随曲轴转角变化的规律如图7 所示。机油的出口流量变化趋势相似,在活塞到达124°之前机油主要聚集在油腔顶部,出油口无机油流出;在活塞换行后,在曲轴转角到达348°附近大量机油聚集在了油腔顶面,此时出口流量为0 kg/s。密度参数较大的纳米机油撞击壁面时速度较大,对壁面的冲击作用更强,从而使出口流量较大,因此整个循环周期内的出口流量由大到小依次为CuO 纳米机油、Al2O3纳米机油、SiO2纳米机油、传统机油。
综上所述,对股骨中下段骨折患者,术后早期应用IK膝关节牵伸康复系统进行静态进展性牵伸可以明显改善患者下肢疼痛和膝关节主动关节活动度,提高患者膝关节功能活动,并且不增加骨不连的风险,具有良好的临床疗效及安全性,在临床治疗中值得进一步推广。

图7 机油出口质量流量
4.1.3 充油率随曲轴转角的变化规律
图8 为标定转速下不同纳米机油瞬态流动的规律。研究发现机油的充油率随曲轴转角变化的趋势基本相似但大小存在差异。当活塞从上止点下行到达90°之前,大量的机油都聚集在油腔的顶部,出油通道无机油流出,机油充油率不断增加,在曲轴转角达到143°时油腔内机油充油率达到最大值。在曲轴转角为150°时,机油离开油腔顶部,大量机油处于悬浮的状态,部分机油从出口通道流出,使充油率不断减小。活塞从下止点上行到达270°之前由于大量机油聚集在油腔底部,充油率继续减小,在曲轴转角到达291°时充油率达到了最小值。当机油脱离油腔底面,向顶面冲击时,流出出口通道的机油减少,充油率又开始逐渐地增加,从而达到上止点完成一个循环。

图8 机油填充率随曲轴转角变化的规律
综上所述由于同种体积分数下的纳米机油喷入油腔的体积量是相同的,但密度较大的纳米机油加速度较大,冲击上下壁面更强烈,流出通道的纳米机油体积量更多,使内冷油腔内的瞬态充油率从大到小依次为传统机油、SiO2纳米机油、Al2O3纳米机油、CuO 纳米机油。
4.1.4 内冷油腔内机油瞬态分布特性分析
图9~图12 为内冷油腔振荡运动过程中机油的瞬态分布。由于机油具有惯性力,在活塞下行到曲轴转角为120°时,大量的机油仍聚集在油腔的顶部,机油离开顶部区域在曲轴转角为150°时大量机油处于悬浮的状态。在到达下止点时,大量机油聚集到了油腔的底部。活塞又从下止点往上止点开始做加速运动,在曲轴转角到达270°之前大量机油又由于惯性力的作用聚集在油腔的底部。在活塞运动到曲轴转角为300°时大量的机油处于悬浮状态,从而达到上止点完成一个循环。由此可见,同种体积分数的纳米机油和传统机油在油腔内的瞬态分布并无明显的差异。
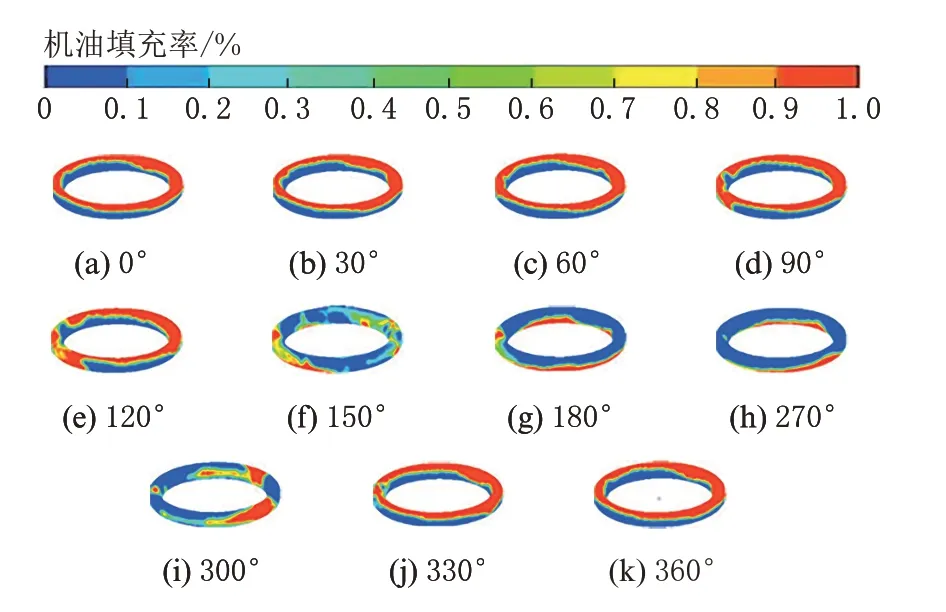
图9 传统机油在不同曲轴转角下的流态
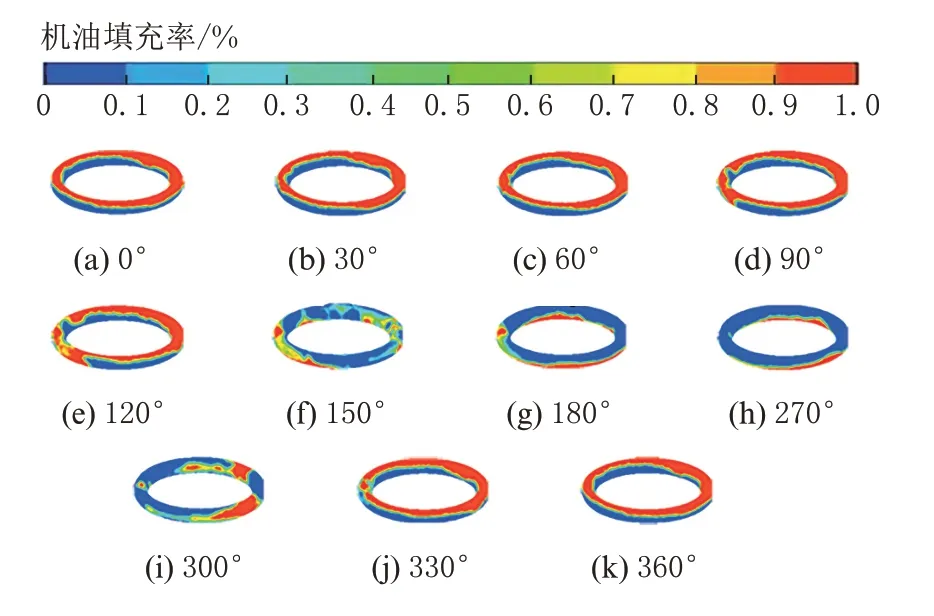
图10 Al2O3机油在不同曲轴转角下的流态
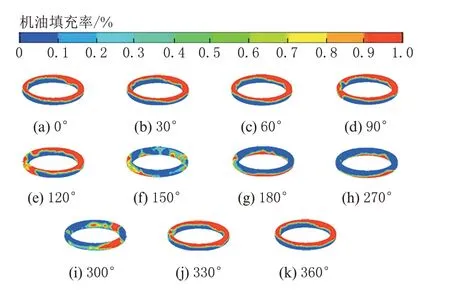
图11 CuO 机油在不同曲轴转角下的流态
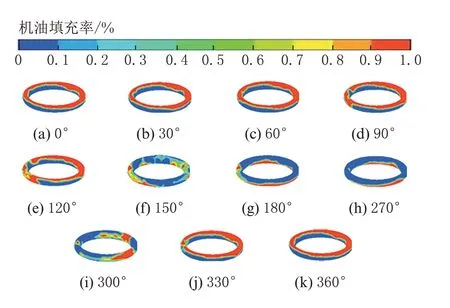
图12 SiO2机油在不同曲轴转角下的流态
4.2 传热系数随曲轴转角的变化规律
纳米颗粒的导热系数比机油大,且纳米颗粒的加入改变了机油的物性参数。图13 为发动机转速为3 200 r/min 时不同体积下4 种机油的传热系数随曲轴转角变化的规律。
从图13 可以看出活塞下行过程中油腔壁面的传热系数峰值大于活塞上行过程中的油腔壁面传热系数峰值,且随着纳米机油体积分数的增加,油腔壁面的传热系数显著增加。当纳米颗粒体积分数为1%、3%、5% 时Al2O3、CuO、SiO2纳米机油传热系数最大值均出现在曲轴转角为118°时,最小值均出现在曲轴转角266°时。纳米机油的最大传热系数、最小传热系数及平均传热系数如表4 所示,可以发现纳米机油的传热系数都高于传统机油。采用式(15)计算纳米机油传热系数的相对变化率,在体积分数为1% 时,相比于传统机油,Al2O3、CuO、SiO2纳米机油的传热系数增大并不明显,分别增大了3.3%、5.2%、1.7%。随着体积分数的增加,纳米机油的平均传热系数变化率增大(表4)。其原因为机油物性参数存在差异,密度较大的机油惯性力较大,机油冲击油腔壁面更加强烈,从而强化了传热,因此不同的体积分数下油腔壁面平均传热系数均是从大到小为CuO纳米机油、Al2O3纳米机油、SiO2纳米机油、传统机油,且随着纳米机油体积分数的增加,传热系数增加。
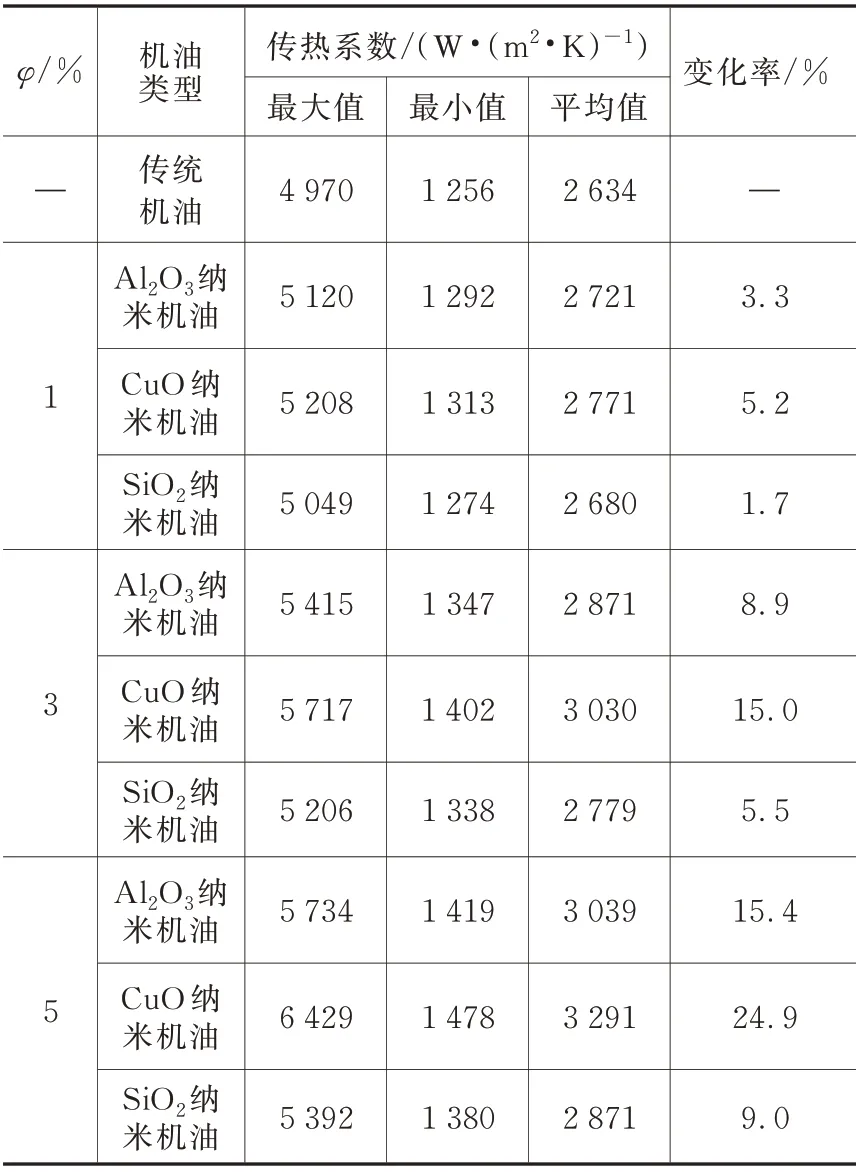
表4 传统机油及不同体积分数的纳米机油传热系数
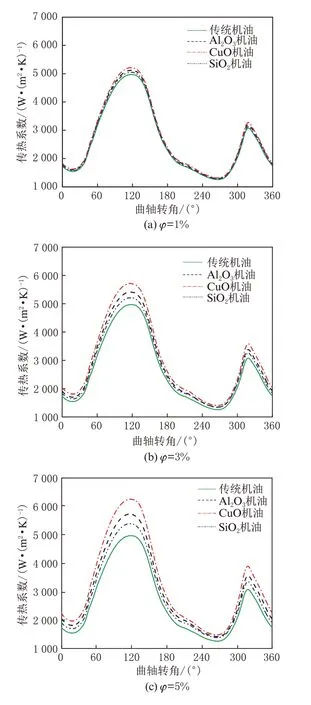
图13 不同纳米颗粒体积分数下流体传热系数随曲轴转角的变化
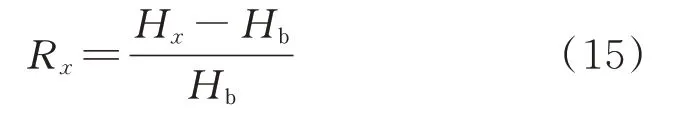
式中,Hx为x类型流体(Al2O3、CuO、SiO2)的平均传热系数;Hb为传统机油的平均传热系数;Rx为Hx相对于Hb的变化率。
4.2.1 机油黏度对内冷油腔换热能力的影响
研究发现,随着纳米机油体积分数的增加,油腔壁面的平均传热系数显著增加。从式(11)~式(14)可以看出,随着体积分数的增加,纳米机油的密度、黏度、导热系数均增加,但比定压热容减小。导热系数的增加会使纳米机油的对流传热系数增加,强化了传热能力;密度的增加可以使机油的惯性力增强,机油冲刷壁面更强烈,从而强化换热过程;纳米机油比热容的降低导致散热能力减弱,弱化了油腔的换热性能;纳米机油黏度的增加导致附着在壁面的流体油膜厚度增加,从而弱化了油腔的传热。但最终,纳米机油传热系数都是随着体积分数的增加而增加。
为了深入探究纳米流体强化油腔换热性能增强的机理,假设了4 类油腔模型。第1 类是在相同的条件下以相同的变化率设置了黏度分别为2.40 g/(m·s)、2.61 g/(m·s)、2.84 g/(m·s)的油腔模型A1、B1、C1,对壁面传热系数进行了监测,如图14 所示。结果表明,黏度为A1、B1、C1 的油腔模型流体的平均传热系数为3 263 W/(m2·K)、3 133 W/(m2·K)、3 012 W/(m2·K),B1、C1 模型的流体模型传热系数相比A1 分别降低了3.9%、7.6%。综上可以看出随着流体黏度的增加,传热系数降低,弱化了油腔的传热。
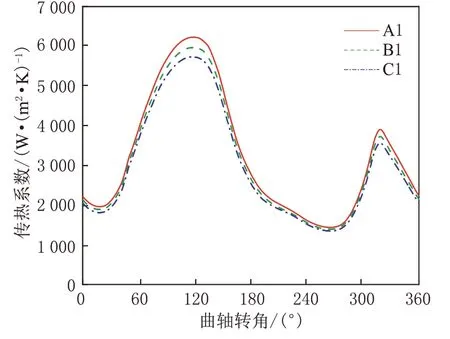
图14 不同黏度模型的传热系数随曲轴转角变化的规律
4.2.2 机油密度对内冷油腔换热能力的影响
为了探究壁面传热系数随纳米机油体积分数的增加而增大的机理,假设第2 类油腔模型:在相同的条件下,同样以8.75% 的变化率设置了密度为897 kg/m3、975 kg/m3、1 061 kg/m3的油腔模型A2、B2、C2。其传热系数如图15 所示,可以看出随着流体密度的增加,油腔壁面的传热系数增加。A2、B2、C2 油腔模型的平均传热系数分别2 699 W/(m2·K)、2 849 W/(m2·K)、3 014 W/(m2·K),B2、C2 模型的流体传热系数相比A2 模型分别增加了5.6%、11.7%。综上可知,在相同条件下随着流体密度的增加,惯性力增加,冲击壁面更加强烈,从而强化了油腔的换热能力。

图15 不同密度模型的传热系数变化
4.2.3 机油比热容对内冷油腔换热能力的影响
为了深入分析纳米机油比定压热容对油腔壁面换热能力的影响,假设了第3 类油腔模型:在相同条件下以相同的变化率设置比热容为2 203 J/(kg·K)、2 011 J/(kg·K)、1 836 J/(kg·K)的油腔模型A3、B3、C3。图16 为这3 种模型传热系数对比。由图16 可以看出,随着流体比热容的降低,油腔壁面的传热系数降低,B3、C3 模型的传热系数相比A3 模型降低了2.5%、5.0%。综上可知,随着纳米颗粒体积分数增加,比热容的降低弱化了油腔的传热。

图16 不同比热容模型的传热系数变化
4.2.4 机油导热系数对内冷油腔传热能力的影响
根据上文的导热系数模型可知,随着纳米颗粒体积分数的增加,纳米机油的导热系数增加。图17为流体导热系数对油腔壁面传热能力的影响。在相同条件下以相同变化率设置了第4 类油腔模型,导热系数分别为0.144 19 W/(m·K)、0.157 19 W/(m·K)、0.172 45 W/(m·K),依次记为油腔模型A4、B4、C4。研究发现,随着导热系数的增加,油腔壁面传热系数增加,B4、C4 模型的传热系数相比A4 模型分别增加了9.0%、19.5%,即流体导热系数的增加强化了油腔换热能力。
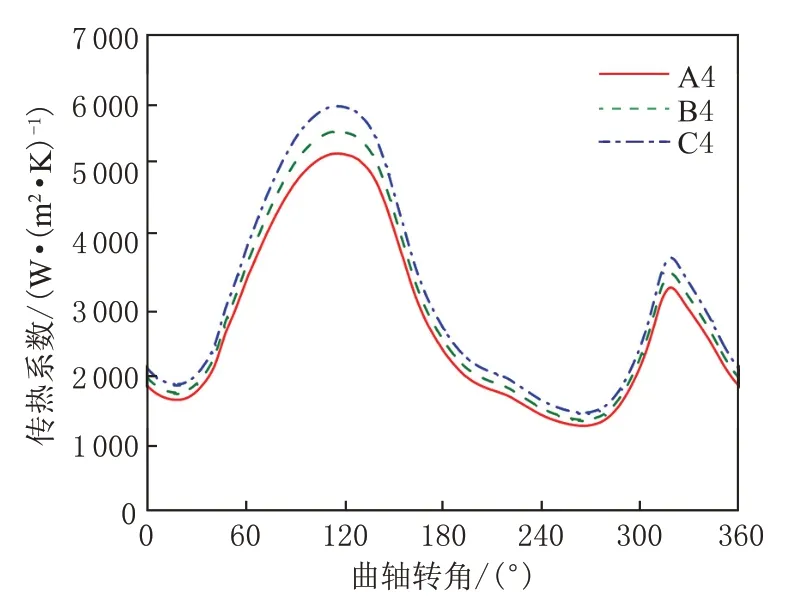
图17 不同导热系数模型的传热系数变化
综上所述,由图14~图17 可知随着纳米颗粒体积分数的增加,虽然黏度的增加和比热容的降低会弱化油腔壁面的传热效果,但密度的增加、导热系数的增加强化传热效果更显著,即密度和导热系数起到了决定性的作用,使纳米流体传热系数随着纳米颗粒体积分数的增加而显著增加。
5 结论
(1)纳米流体有良好的导热性能,可提升内冷油腔的振荡冷却性能,不同的纳米流体在振荡过程中的强化传热效果不同。
(2)纳米颗粒的加入改变了流体的物性参数,相比传统机油,纳米流体的传热效果更好,且随着纳米流体体积分数的增加,油腔壁面的传热系数增加;但纳米颗粒的加入并没有改变油腔瞬态机油的分布。
(3)纳米机油与传统机油之间的物性参数存在较大的差异,密度较大的纳米机油惯性力大,加速度较大,从而冲击壁面的作用力更强烈,出油通道流出的机油体积量更多。相同体积分数下的纳米机油和普通机油在油腔内的瞬态机油充油率从大到小依次为传统机油、SiO2纳米机油、Al2O3纳米机油、CuO 纳米机油。
(4)机油的黏度和密度、比热容、导热系数都能影响油腔壁面的传热系数,机油黏度的增加、比热容的降低会使壁面的传热系数降低,密度和导热系数的增加会使壁面的传热系数增加,但密度和导热系数的增加对油腔的传热能力起到了决定性作用。
(5)CuO 纳米机油的密度参数最大,惯性力最大,撞击壁面的速度最大,冲击壁面更加强烈,强化了油腔的传热能力。
