GNSS/INS紧组合的新息优化抗差估计欺骗检测算法
2022-07-06吕志伟周玟龙周舒涵艾宏岩
柯 晔,吕志伟,周玟龙,邓 旭,周舒涵,艾宏岩
(1. 战略支援部队信息工程大学,郑州 450000;2. 31618部队,福州 350000;3. 31700部队,辽阳 111000)
全球卫星导航系统(Global Navigation Satellite System, GNSS)和惯性导航系统(Inertial Navigation System, INS)的组合导航系统具有两者互补误差特性,GNSS具有能够在全球范围内提供全天候连续性的位置、速度和时间(Position, Velocity & Time, PVT)服务的优点[1],而INS具有独立自主,连续工作,提供短期抗干扰能力等优点,两者组合增加了系统的冗余度和可靠性。然而,由于GNSS信号功率低和结构公开的特点,使得GNSS服务易受欺骗干扰的影响,欺骗干扰是指干扰源产生与真实信号高度相似的欺骗信号或转发真实信号欺骗目标接收机,迫使其生成错误和可能危险的信息[2,3]。在GNSS/INS组合导航系统中,若GNSS模块锁定欺骗信号并输出错误的信息,然后影响滤波更新阶段状态的误差估计值,而解算错误的导航数据。同时错误的状态误差估计值通过信息融合反馈至INS,最终影响GNSS/INS组合导航系统[4]。因此,有必要进行实时和准确的欺骗检测,以保证组合导航系统的可靠性。
GNSS/INS紧组合欺骗检测方法主要是基于卡尔曼滤波新息向量作为检测统计量[4],具有成本低、效率高和计算量小等优点,是一种应用广泛的假设检验方法。该方法可分成“快照法”和“连续法”[5],“快照法”是以当前时刻的新息向量构成检验统计量,对阶跃式欺骗干扰较为敏感;“连续法”是将一段时间内的新息向量构成检验统计量,对斜坡式欺骗干扰较为敏感。然而,GNSS/INS组合导航系统欺骗干扰检测存在的难点是组合导航闭环校正机制[6]和缓慢增长的斜坡式欺骗检测的时延问题。
针对组合导航闭环校正机制问题,ZHANG Chuang等[7]提出了基于抗差估计和“检测窗口”的改进检测算法,其核心思想是选择两个合适的阈值计算权重因子,并自适应调整测量噪声协方差矩阵,降低受欺骗干扰测量值的权重,从而自适应调整增益矩阵,在单路通道受到0.5 m/s斜坡式干扰时,改进的算法比传统算法的检测时长缩短了10 s,漏检率降低了9%。张超等[4]提出了新息速率抗差估计检测算法,该算法能够有效地抑制欺骗干扰对状态向量的影响,提高了数据使用率和算法可靠性,在单路通道0.1 m/s的缓慢增长的斜坡式欺骗干扰漏检率和虚警率维持在4%以内。但这两种算法对缓慢增长的斜坡式欺骗干扰,尤其是小于0.1 m/s斜率的欺骗干扰,其检测时间过长甚至检测不敏感。
针对缓慢增长的斜坡式欺骗检测时延问题,Bhatti等[8]提出了采用卡尔曼滤波实时估计新息速率的方法来检测GNSS测量值是否存在异常,该方法有效提升了检测时间,但受组合导航闭环校正影响,其余正常通道的新息速率也受到影响,在单路通道受到0.1 m/s的欺骗干扰时,检测时间为110 s,同时该方法设计了两层滤波器机制,增加了实际操作的复杂度。许睿等[9]提出了MEDLL的欺骗信号检测方法,能够成功检测并识别出2 m/s的斜坡式欺骗,但其斜坡斜率较大,很难适用于0.1 m/s的缓慢增长的斜坡式欺骗干扰。近五年,部分学者研究了神经网络[10]、支持向量机[11]等欺骗检测算法,但计算复杂、兼容性弱且成本较高。
为解决上述欺骗检测的难点,本文首先构建了GNSS/INS紧组合测量层面欺骗干扰模型,然后针对斜坡式欺骗检测时间长甚至检测不敏感等问题,提出了一种基于GNSS/INS紧组合的新息优化欺骗检测算法,新算法对缓慢增长的斜坡式新息检测量进行了优化,结合抗差估计自适应调整增益矩阵并合理选择“检测窗口”,进一步提高了缓慢增长的斜坡式欺骗干扰的检测效率和检测性能。最后通过实验仿真验证了所提出算法的合理性和可行性。
1 欺骗干扰仿真模型
本文从测量层面建立GNSS/INS组合导航系统欺骗干扰仿真,可实施性较强,能有效避免复杂的信号层面仿真。假设第i颗卫星在时间t内的真实伪距测量值(t)模型为:

其中,c是光速,τ(i)是信号传播时延,δtr和δt(i)是接收机钟差和卫星钟差。假设∇τ是由欺骗器在目标接收机引入的附加信号时延,那么得到欺骗伪距测量值L和真实伪距测量值L的关系就相当于相差一个伪距附加值s(t),此时的测量层面的s(t)等效于信号层面的c∇τ。由此,推导测量层面的欺骗干扰模型为:
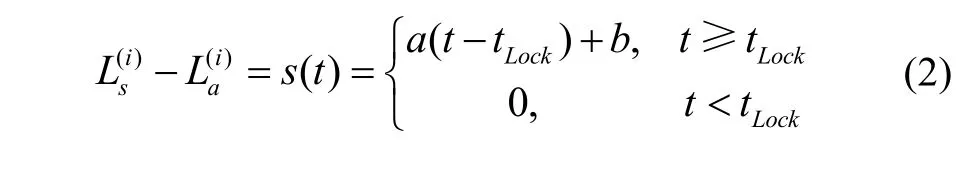
其中,tLock是欺骗信号锁定目标接收机跟踪环路的时刻,a(t-tLock)+b是欺骗干扰的伪距附加值,a(t)是斜率,b是欺骗伪距与真实伪距的伪距偏差。当a≠0,b=0时,代表阶跃式欺骗;当a=0,b≠0时,代表斜坡式欺骗。
2 基于GNSS/INS紧组合的抗差估计新息欺骗检测算法
GNSS/INS紧组合的新息抗差估计欺骗检测算法,是将卡尔曼滤波估计得到的新息向量作为检测统计量来判断是否存在欺骗干扰。设在k时刻,无欺骗新息向量rk是观测向量Zk与计算得到的预测观测量的差值,其对应的协方差矩阵Vk是由观测矩阵Hk,测量状态向量协方差与观测噪声Rk之和,具体表达式如下:
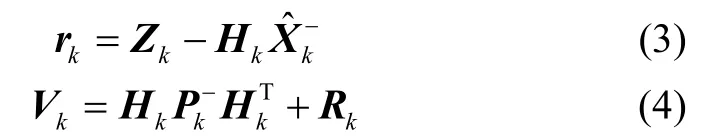
当k时刻有欺骗时,观测向量为:
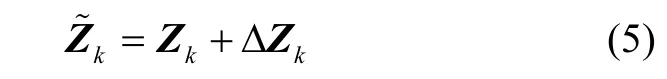

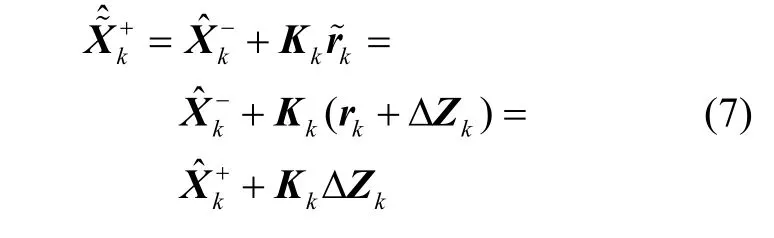
则k+1时刻欺骗新息为:

由此可得,当k时刻有欺骗干扰时,会影响k+1时刻的新息向量,即k+1时刻的新息向量减少了Hk+1Φk K kΔZk,使得前后时刻的测量存在相关性。
2.1 快照法
“快照法”是一种系统级方法,它不能识别错误测量,但能及时识别和隔离欺骗干扰影响的测量值。定义k时刻新息向量的第i个测量值(i=1…n,n为可见卫星的通道)和对应的协方差矩阵,在k时刻的归一化的新息值ωi为:

如果接收到的第i路通道是真实信号,那么新息向量的第i个测量值不存在欺骗干扰,则原假设为H0:ωi~N(0,1),ωi服从标准正态分布;否则备择假设为H1:ωi~N(δ,1),δ为非中心参数,此时ωi服从非中心正态分布。在理想情况下,设有n路通道,全局虚警率为Pfa[12],使得当原假设成立时,则对应的第i个检验统计量的虚警率为α0[9]:
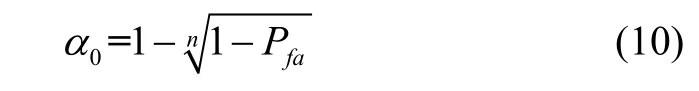
根据假设检验原理,判断是否存在欺骗干扰的检测标准为:

2.2 连续法
“连续法”是代表一段时间内的新息向量构成检验统计量,可用于单个测量值的检测,构成平均归一化新息,其中,一段时间内就构成了“检测窗口”。若测量值受欺骗,则所对应测量值检验统计量可以反应这段时间内测量值误差的累积,直到超过阈值,表明存在欺骗干扰。定义检测窗口为L,从k-L+1时刻到k时刻的第i个测量值的平均归一化新息[13]表达式如下:
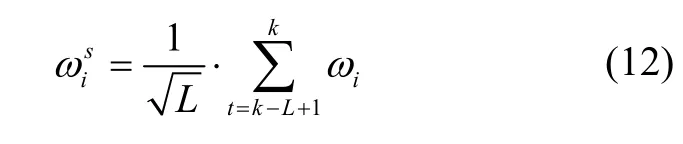
同样的,“连续法”在判断是否存在欺骗干扰的检测标准时与“快照法”类似,只不过检验统计量变为了。但这两种方法有局限性,当其中一个通道受到欺骗干扰影响时,闭环校正机制会影响其他通道偏离正常新息值,从而发生漏检或虚警的情况。
2.3 基于新息抗差估计的连续法
针对2.2节所述方法的局限性,引入了抗差估计法,使用IGG-3等价权函数[14],计算等价权wi,三段函数表示如下:


当发生斜坡式欺骗干扰时,若检验统计量介于Td1和Td2之间,将调整归一化新息权重小于1,这意味着该新息测量值在卡尔曼滤波器测量更新中的权重会降低,而滤波器精度会提高,反过来又会提高下一次的欺骗检测性能。综上所述,引入抗差估计等价权函数,能够有效地抑制因受到欺骗干扰的卫星道通影响正常通道偏离新息值,达到了削弱欺骗干扰的影响,提高了欺骗检测的效率。
3 基于GNSS/INS紧组合的新息优化抗差估计欺骗检测算法
针对上述情况,对于组合导航系统的GNSS测量发生了缓慢增长的斜坡式欺骗干扰,例如,小于0.1 m/s的斜率的欺骗干扰,传统检测方法不理想。提出了一种基于GNSS/INS紧组合的新息优化欺骗检测算法,新算法能够有效解决缓慢增长的斜坡式的检测时间较长甚至检测不敏感问题,达到缩短检测时间和提升检测性能的效果。
假设在第i次测量中出现斜坡式欺骗干扰,其在滑动窗口中的实际幅值从A1增加到A2,而归一化幅值则从a1增加到a2,且归一化幅值的斜率保持不变。改进的归一化平均新息的推导过程,首先从“快照法”进行推导,而后过渡到改进的归一化平均新息“连续法”,具体推导如下:
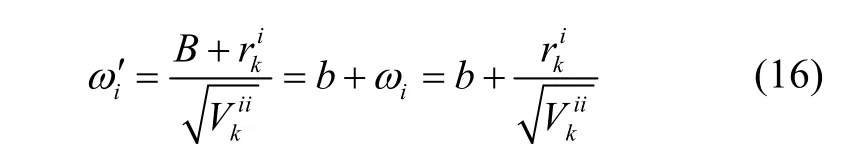


如果a1∙a2≥0且L较大时,则:

也就是说,在大多数情况下,如果L足够大时,例如L≥10,改进的“连续法”在处理斜坡式欺骗干扰时具有较好的检测性能。同时,随着“检测窗口”有效长度L的增加,“连续法”处理斜坡式的能力也随之增加,而该方法的计算效率将降低。有效长度L仅指包含受欺骗干扰的测量值的窗口长度,即在一段时间内,不包含受欺骗干扰的测量长度可以被称为“浪费长度”,这对检测性能是有负面影响的。因此,“检测窗口”不应过长,要按照实际情况合理地选择有效长度L。
由此,判断是否存在斜坡式欺骗干扰的检测标准为:

综上所述,基于GNSS/INS紧组合的新息优化欺骗检测算法流程图如图1所示。具体的步骤如下:

图1 新算法的欺骗检测流程图Fig.1 Spoofing detection flow chart of the new algorithm
1)归一化新息优化。基于GNSS/INS紧组合的新息算法,并优化每个测量的归一化新息。
3)滤波器测量更新。在所有局部测试完成后,计算等价权矩阵,然后进行滤波器测量更新。
4)k时刻欺骗检测过程完成,在k+1时刻返回步骤1)。
4 结果与讨论

4.1 仿真条件

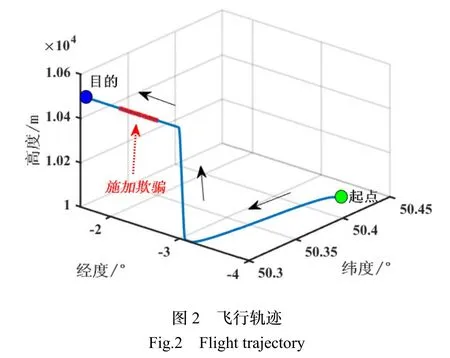
4.2 仿真结果与分析
(1)试验1
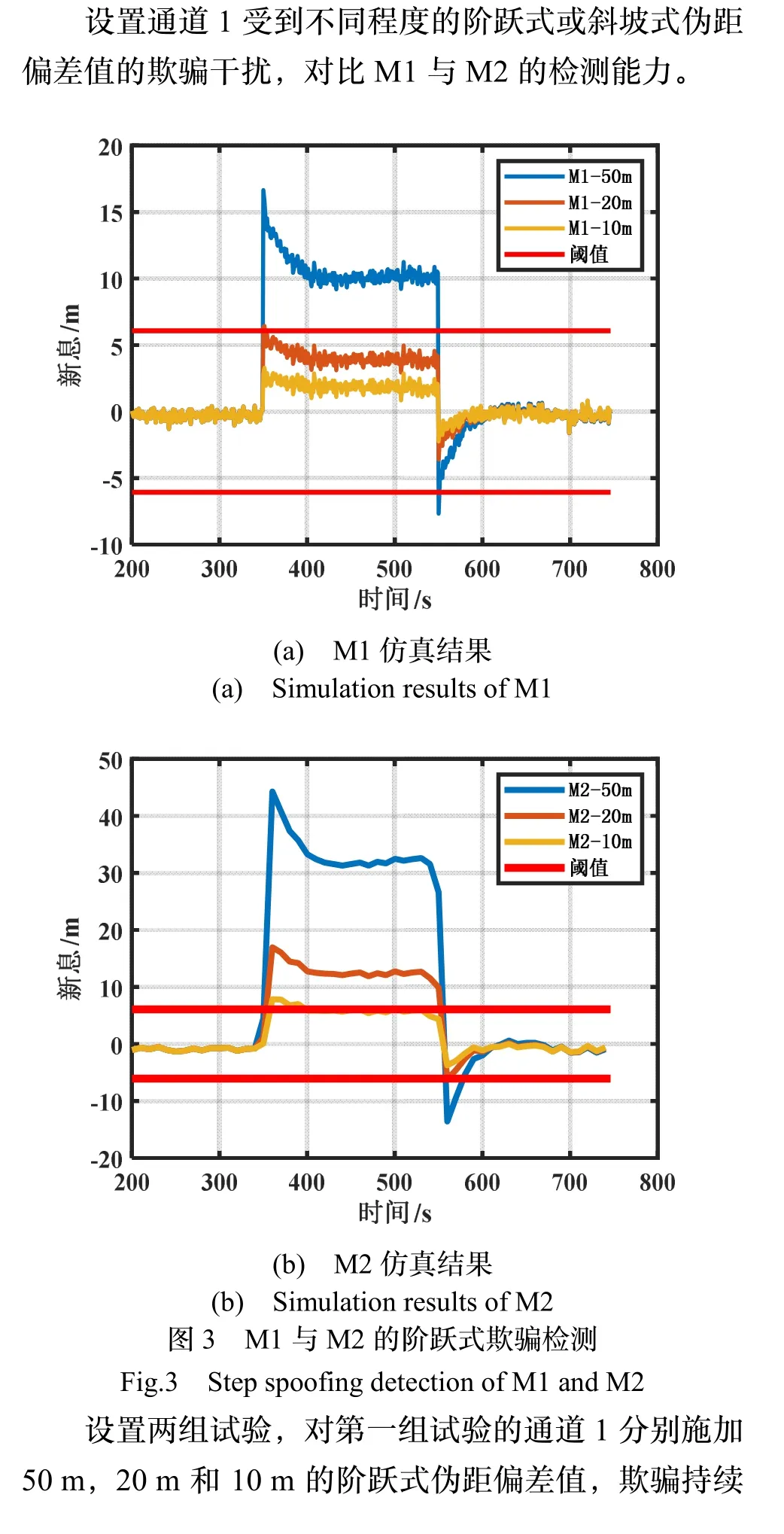

对第二组实验的通道1分别施加0.5 m/s,0.2 m/s和0.1 m/s的斜坡式伪距偏差值,斜坡式欺骗仿真结果如图4所示,由数据表明:图4(a)是M1仿真结果图,显示了通道1对0.5 m/s和0.2 m/s的斜坡式欺骗的检测时间分别为44 s和135 s,而对0.1 m/s的斜坡式欺骗检测无效。图4(b)是M2仿真结果图,显示了通道1对0.5 m/s,0.2 m/s和0.1 m/s的斜坡式欺骗的检测时间分别为20 s,50 s和100 s,可知,M2的检测时间比M1分别缩短了16 s,85 s和100 s,平均缩短了67 s,由此得出M2在处理斜坡式欺骗时具有较好的检测效率和检测性能。
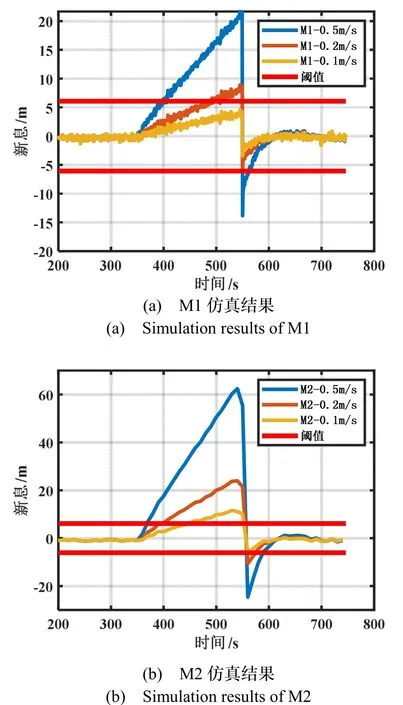
图4 M1与M2的斜坡式欺骗检测Fig.4 Ramp spoofing detection of M1 and M2
结合图3和4数据得出:在道通1受到阶跃式欺骗时,M2比M1检测时间平均延长了10 s,但M2检测性能更优;在通道1受到斜坡式欺骗时,M2比M1检测时间分别缩短了54.5%,63%和100%,平均缩短了72.5%,且M2检测性能更优。故,M2的检测效率和检测性能相对M1更优。
(2)试验2
设置通道1受到0.1 m/s的斜坡式伪距偏差值的欺骗干扰,对比M2与M3的检测能力,验证抗差估计能够抑制正常通道因欺骗干扰而偏离正常值的效果。
对通道1施加0.1 m/s的斜坡式欺骗伪距偏差,M2与M3的斜坡式欺骗检测仿真结果如图5所示,由数据表明:图5(a)是M2仿真结果图,显示了通道1的检测时间为100 s,但通道3、4和5均受到了不同程序的欺骗干扰影响,导致其新息偏离正常值;其中通道4超过了阈值Td2,出现了虚警情况。图5(b)是M3仿真结果图,显示了通道1检测时间为100 s,而且其余通道的新息值没有发生偏离,证明抗差估计有效削弱了欺骗干扰引起其他道通的影响。但M3方法具有局限性,可以看出检测时间并没有发生缩短。
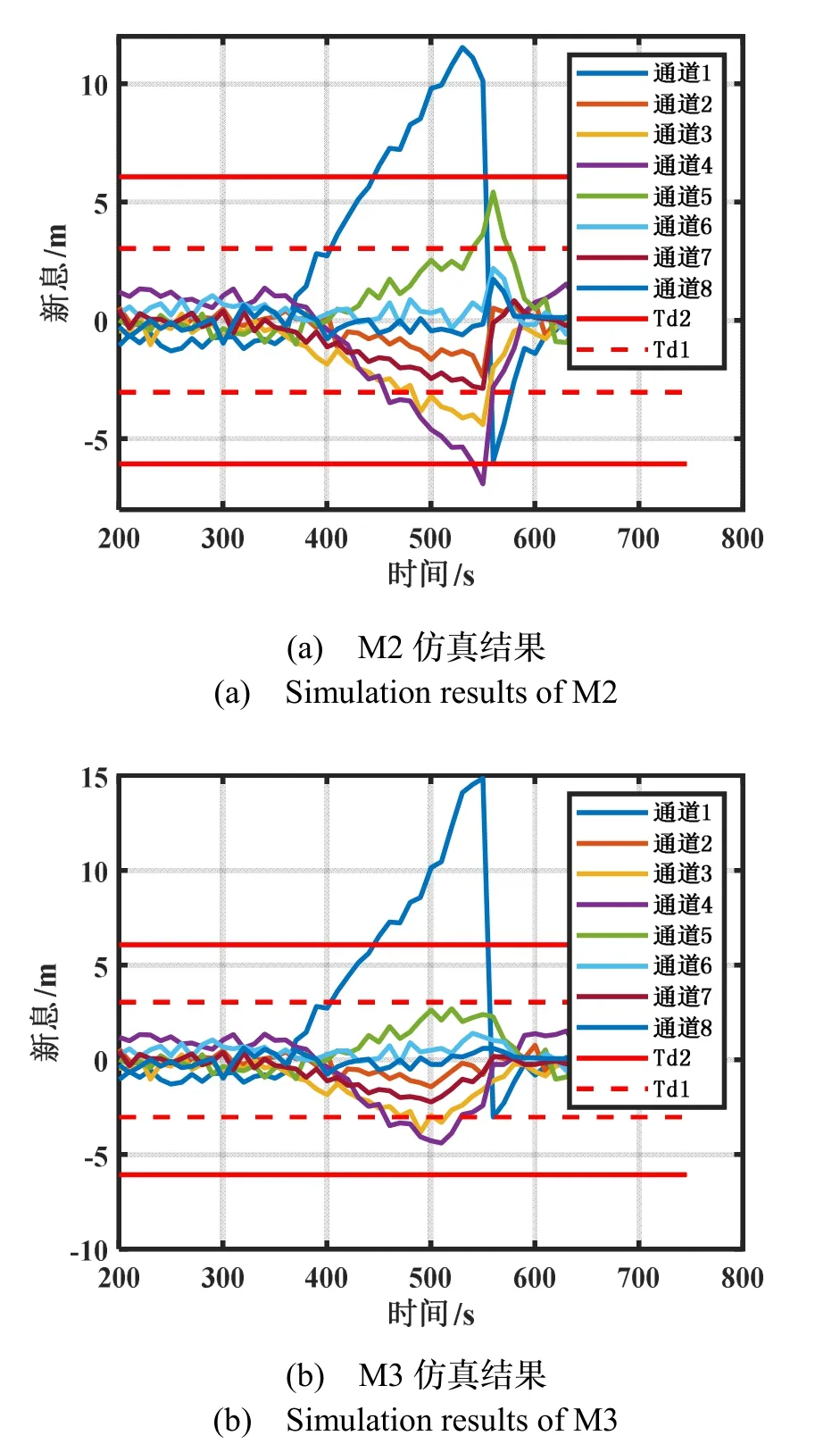
图5 M2与M3的斜坡式欺骗检测Fig.5 Ramp spoofing detection of M2 and M3
为了进一步说明M3的优势,表3显示了试验2的100次循环的蒙特卡罗仿真情况。其中,“*”表示受欺骗干扰通道,后面不再赘述。
结合图5和表3数据表明:1)通道1受到斜坡式0.1 m/s欺骗时,M3比M2的检测时间均为100 s。2)对于漏检率,M2与M3均为0。对于虚警率,M2的通道3、4和5分别为2%、96%和0,而M3对应分别为0%、6%和0,M3比M2的虚警率降低了2%、90%和0。由此,验证了M3的抗差估计效果,能够很好地削弱新息偏离正常值的效果。
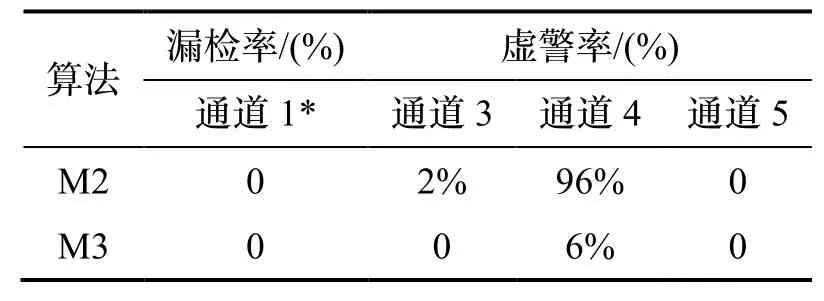
表3 试验2蒙特卡罗仿真结果Tab.3 Monte Carlo simulation results of test 2
(3)试验3
针对试验2中M3对较小的斜坡式欺骗检测的局限性,特别是对于小于0.1 m/s的斜率欺骗检测时间较长问题,对试验3设置了两组试验,比较M3与M4的检测能力。
第一组试验对通道1施加0.1 m/s的斜坡式伪距偏差值,M3和M4的斜坡式欺骗检测分别如图5(b)和6所示,由数据表明:图5(b)是M3仿真结果图,显示了通道1的检测时间为100 s,其余通道正常。图6是M4仿真结果图,显示了通道1检测时间为70 s,M4相对M3的检测时间缩短了30 s。

图6 M3与M4的斜坡式欺骗检测Fig.6 Ramp spoofing detection of M3 and M4
第二组试验对通道6施加0.1 m/s的斜坡式伪距偏差值,图7是通道6受欺骗时M3与M4的欺骗检测对比图,其中数据表明:M3检测时间为110 s,而M4检测时间为60 s,M4相对M3的检测时间缩短了50 s。两组试验表明,在处理缓慢增长的斜坡式欺骗检测时,M4的检测算法优于M3。
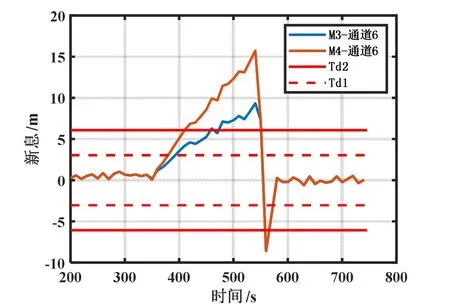
图7 通道6受欺骗时M3与M4的欺骗检测对比Fig.7 Comparison of M3 and M4 spoofing detection when channel 6 is spoofed
为了更好说明M4优于M3,表4显示了实验3的100次循环的蒙特卡罗仿真情况。
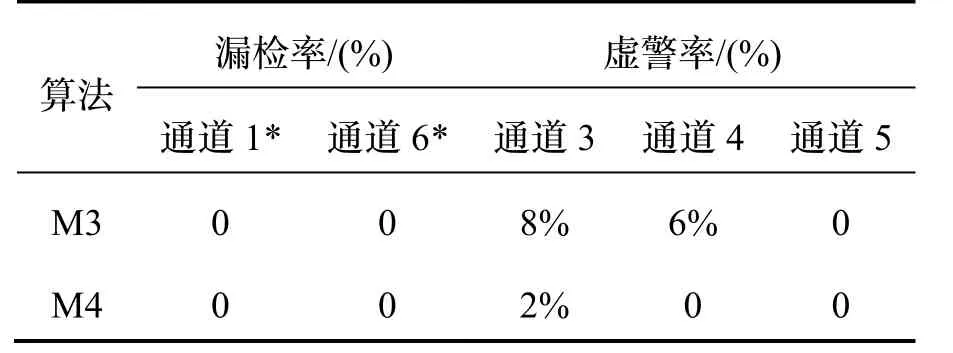
表4 试验3蒙特卡罗仿真结果Tab.4 Monte Carlo simulation results of test 3
结合图5(b)、6和7和表4数据表明:1)对通道1施加0.1 m/s的斜坡式欺骗时,M4比M3的检测时间缩短了30%;对应通道6,检测时间缩短了45.5%。结合通道1和6,M4比M3检测时间平均缩短了37.8%。2)对于漏检率,M3和M4均为0%。对于虚警率,M3的3路通道分别为8%、6%和0;M4对应通道分别为2%、0和0,M4对比M3的虚警率分别降低了6%、6%和0,平均降低了4%。由此可验证在处理缓慢增长的斜坡式欺骗干扰时,M4能够缩短检测时间和提升检测性能。
(4)试验4
设置通道1、2和3同时受到0.1 m/s斜坡式的伪距偏差时,对比M3、M4的3路通道检测情况。
由图8所示是3路通道受斜坡式M3、M4的欺骗检测对比图,其中数据表明:图8(a)显示通道2检测时间100 s,而通道1和3检测无效,出现漏检情况。图8(b)显示多通道欺骗检测正常,通道1、2和3的检测时间分别为90 s、70 s和100 s。
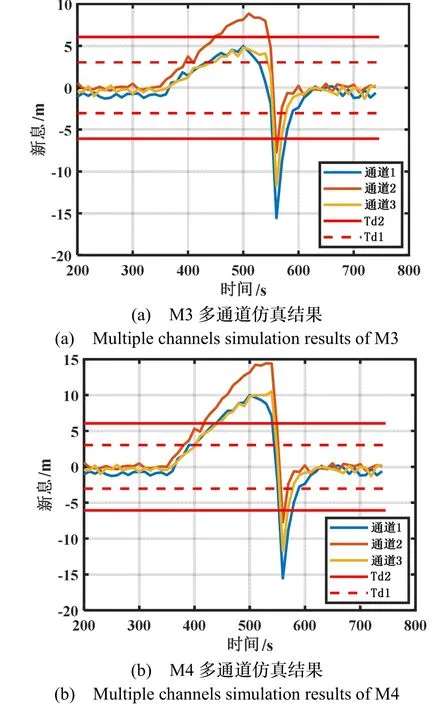
图8 多路通道受欺骗时M3与M4的欺骗检测对比Fig.8 Comparison of M3 and M4 spoofing detection when multiple channels are spoofed
为了更好说明多通道欺骗检测算法M4优于M3,表5显示了试验4的100次循环的蒙特卡罗仿真情况。

表5 试验4蒙特卡罗仿真结果Tab.5 Monte Carlo simulation results of test 4
结合图8和表5数据表明:1)对通道1、2和3同时施加0.1 m/s的斜坡式欺骗时,通道2中M4比M3的检测时间缩短了30%;通道1和3中M4检测有效,而M3检测无效。2)对于漏检率,M3的通道1、2和3分别为42%、47%和51%;M4的对应通道分别为0、0和0,M4对比M3的漏检率分别降低了42%、47%和51%,平均降低了46.7%。对于虚警率,M3的通道4和5分别为75%和27%;M4对应通道分别为42%和23%,M4对比M3的虚警率分别降低了33%和4%,平均降低了18.5%。由此可知,在处理多通道缓慢增长的斜坡式欺骗干扰时,M4能够缩短检测时间和提升检测性能。
5 结 论
基于GNSS/INS紧组合的新息抗差估计欺骗检测算法是一种常用欺骗干扰检测算法,能够很好地削弱组合导航闭环校正机制对正常新息值的影响,但对缓慢增长的斜坡式欺骗干扰检测时间过长,甚至检测不敏感。本文提出了一种基于GNSS/INS紧组合的新息优化抗差估计欺骗检测算法,新算法通过调整伪距参数,优化了新息检测量,进一步提高了缓慢增长式欺骗干扰的检测处理能力。仿真结果表明,在检测单通道缓慢增长的欺骗干扰时,新算法检测时间平均缩短了37.8%,漏检率为0,虚警率平均维持在0.7%以内;在检测多通道时,新算法检测时间平均缩短了30%,漏检率平均降低了46.7%,虚警率平均降低了18.5%。与传统算法相比,新算法在检测缓慢增长的斜坡式欺骗干扰时,具有检测快、漏检率和虚警率低的优势,在民用和军用无人机的应用领域具有重要意义。
未来工作展望:1)在导航系统的完好性检测级别保护水平上,通过改变虚警率,研究检测概率的变化。2)增加实测数据对改进算法进行验证。3)对多路通道欺骗检测算法的优化和识别算法的研究。
