地球自转模型误差对高精度惯导系统定位精度的影响分析
2022-07-06严恭敏戴晨杰陈若彤
严恭敏,戴晨杰,陈若彤
(西北工业大学 自动化学院,西安 710072)
惯性导航的主要误差源有惯性传感器误差、初始条件误差和导航解算误差。毋庸置疑,惯性传感器及其硬件系统集成的性能在导航精度中发挥着决定性作用。初始条件误差主要是指姿态和方位的初始化误差,尤其是方位对准精度对自主高精度惯性导航会产生重要的影响[1,2]。导航解算误差的影响相对较小,采用多子样、高阶和迭代等不可交换误差补偿算法后[3-6],即使是在高动态恶劣环境下由算法引起的导航误差也可忽略不计。
除上述传统观点中的三种导航误差源外,实际上还有一类误差源经常被忽略了,即导航环境因素误差。惯性导航一般是在地球表面上进行并以地球作为参照物的,惯导系统的外部环境——地球的几何形状、重力场分布以及自转角速度等因素都会影响导航解算精度。近年来,地球的几何形状参数建模已经非常精确,其厘米级误差对长航时惯性定位的百米级以上精度需求的影响可以不予考虑。重力场垂线偏差对惯性导航精度的影响较大,已有不少文献进行了深入的研究[7],重力补偿技术已在航空惯导和测地车惯导零速修正等场合获得了实际应用。目前,在惯性导航领域中尚未发现有文献针对地球自转角速度的影响进行专门研究。
在惯性导航专业中,通常认为地球自转角速度仅在其自转轴方向存在分量,大小为ωie=15.041067178670319°/h ,而在垂直自转轴方向上的角速率均为零。然而,天文学研究显示[8]:由于太阳、月球及行星对地球上赤道隆起部分的作用力矩而导致赤道平面的进动(赤道岁差),其角速率每年约西移50.39 ″,旋转一周约2.6万年;行星对地月质心绕日公转黄道面影响,造成春分点移动(黄道岁差),其角速率每年约东移0.1 ″,而且还会使黄赤交角在21 °55 ″~24 °18 ″范围内变化。这些运动信息表明,地球自转轴在惯性空间中的指向并不是恒定不变的,或者说地球在垂直于其自转轴的方向上存在微小的转动角速率分量,该现象势必对长航时高精度的惯导系统产生不利影响。
在天文大地测量学中,地球定向参数(Earth Orientation Parameters, EOP)是描述地球自转运动规律的一组参数,包含极移、地球自转变化和日长变化(Length Of Day, LOD)。本文根据国际天文联合会(International Astronomical Union, IAU)的岁差章动模型和大地测量学EOP的LOD数据,推导出地球旋转变换矩阵,并获得了求解精确的地球旋转角速度的方法,给出了传统地球自转角速度模型误差的表达式,修正了传统惯导系统误差传播方程,最后进行了长航时高精度惯性导航误差的仿真验证。
1 地球自转角速度模型误差
根据天文学理论,从协议天球坐标系(比如J2000坐标系,简记i系)到协议地球坐标系(比如WGS84坐标系,简记e系)的坐标系转换矩阵为[9]:


其中,ζ、θ、z为三个岁差角参数,ε、Δψ、Δε分别称为黄赤交角、黄经章动和黄赤交角章动,θA为格林尼治视恒星时(Greenwich Apparent Sidereal Time,GAST),xp和yp是瞬时极相对于国际协议原点(Conventional International Origin, CIO)的角度值,Rs(∙)(s=X,Y,Z)表示绕坐标轴旋转的坐标变换矩阵。上述各参数的详细计算或获取方法可参见文献[8,9]。特别地,下面仅对参数θA作详细分析。
格林尼治视恒星时θA是瞬时春分点与格里尼治零度经线之间的夹角,其变化主要取决于地球自转,同时与岁差章动导致瞬时春分点的移动有关。θA的计算公式为:
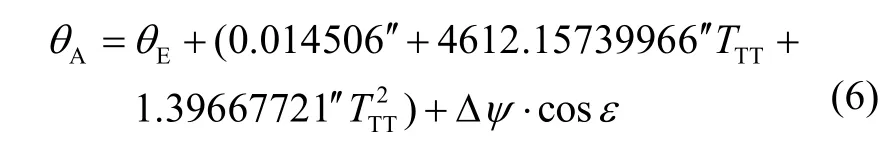

其中,dJDUT1=JDUT1-JD00为J2000.0参考历元至儒略日JDUT1历元时刻的儒略日间隔。
将式(7)对时间求导,可得瞬时地球自转角速率,如下:

式(8)表示的是瞬时地球坐标系(E系)的Z轴相对于惯性坐标系(i系)的瞬时角速率,由于几乎不受极移的影响,也可以认为是协议地球坐标系(e系)的Z轴相对于(i系)的瞬时角速率。
式(8)中的系数便是传统惯导文献给出的地球自转角速率ωie,即有ωie=15.041067178670319°/h ,其含义是e系的Z轴相对于i系的“平均”角速率。实际上,由于地球自转变化(日长变化),即世界时UT1不均匀,使得d(UT1)/dt并不严格等于1,地球自转角速率真值将在常值ωie附近波动。由此可见,传统惯导中的地球自转角速度矢量模型是有误差的,将传统地球自转角速度记为:
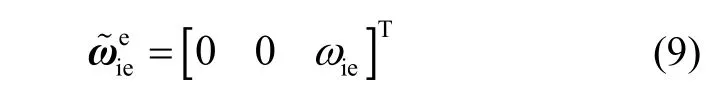
为了更精确地求解地球自转角速度矢量,利用如下方向余弦阵微分方程:

定义地球自转角速度模型误差,记为:
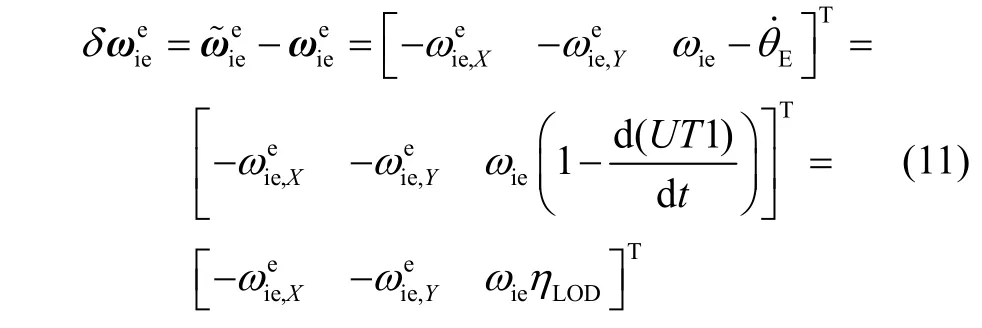
其中,ηLOD为LOD一天之中的相对变化量,可由EOP中的LOD数据(以秒为单位)计算,即有ηLOD=LOD/(24×3600)。
2 惯导误差传播方程修正与误差特性分析
2.1 误差方程推导
选“东-北-天”地理坐标系为导航参考系(简记n系),由惯导系统在地球表面所处的经度λ和纬度L,可得惯导位置矩阵:

式中,sα、cα分别表示sinα和cosα。
对如下角速度坐标转换公式:
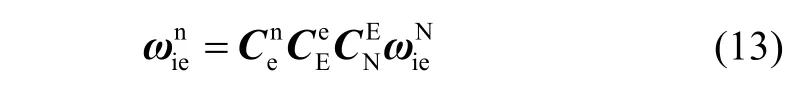

式中,


M1的具体定义详见文献[10];δW为因极移引起的在n系上投影的地球自转误差,注意到,有δWY cL+δWZ sL=0成立,也就是极轴方向的极移误差为零;δω、δω为因岁差章动而引起的地球自转轴的摆动角速率误差(垂直于地球自转轴),它们均是在瞬时天球坐标系(N系)上投影的,不受地球自转的影响。将δ转换到导航系(n系)过程中,将受到地球自转角矩阵RZ(-θE)的调制作用。x p、y p是瞬时极相对于CIO的角度值,其方向分别是从CIO指向0 °经线和270 °经线方向,两者大小一般小于0.5 ″。
将式(14)代入捷联惯导误差传播方程[10],可求得失准角误差φ、速度误差δvn和位置误差δp方程,分别为:

2.2 误差特性分析
首先,在式(15)中,假设极移为0.5 ″,则极移误差δW的幅值约为ωie×0.5′=3.6×10-5°/h;而δ的幅值仅约为1×10-6°/h量级,可见短时间内(比如1 d内)δW比δ的影响大得多。δW在1/4个修拉周期内引起的失准角波动幅值约为3.6×10-5°/h × 84.4 min/4= 0.05 ″。在式(16)中,假设惯导速度vn大小幅值为10 m/s,则由δW引起的加速度误差等效为水平失准角仅约为(2×10 m/s×3.6×10-6°/h) /g=7.2×10-5″。因此,速度误差式(16)的最后一项可以忽略不计,本文所提出的捷联惯导误差传播方程仅需在姿态误差式(15)的最后增加即可。
3 数值仿真验证
3.1 地球自转角速度误差仿真
不考虑极移的影响,调用天文标准库(Standards Of Fundamental Astronomy, SOFA)提供的开源程序(iauPn06a和iauGst06a函数)[11],并从地球自转服务网站(www.iers.org)下载LOD数据[12],计算2000年~2020年间的地球自转角速度误差δ,其三轴分量如图1所示,它们的均值为[-0.008-0.633-0.131]T×10-6°/h。图1(a)(b)显示,X轴和Y轴的波动峰峰值约为1×10-6°/h,该波动主要由章动引起;岁差在N系的Y轴投影形成了Y轴曲线的常值误差;图1(c)中的Z轴均值为负,显示了地球自转角速率的减速现象,Z轴波动反映了地球自转的不均匀,相对不均匀性(稳定度)约为:。

图1 地球自转角速度误差Fig.1 The Earth's angular velocity errors
3.2 长航时纯惯导误差仿真
这里在惯性器件仿真中考虑了地球自转角速率模型误差的影响,但在惯性导航更新算法中仍然采用传统的地球自转参数式(9)。
于地理位置L=0,λ=0处进行静基座纯惯导仿真(高度通道固定不更新),仿真中假设惯性器件是理想无误差的,且假设惯导的初始导航参数(姿态、方位角、速度和位置)准确已知。从2016年1月1日开始,共进行了100 d的纯惯导仿真,导航误差如图2所示。采用捷联惯导误差传播模型式(15)-(17)递推获得的误差曲线与图2重合,验证了误差传播模型的正确性,不再重复展示。

图2 100天纯惯导误差Fig.2 Inertial navigation errors within 100 days
根据图2分析,可得到以下结论:
(1)东向通道中的北向失准角φN和东向速度δVE都比较小,但会随时间不断累积导致经度误差δλ缓慢增加。经度误差δλ主要是由地球自转误差中的Z轴分量δωiNe,Z引起的。不难理解,日长变化LOD乘以地球自转角速率所得角度值,即为惯导系统在该时间段内的经度解算误差。
(2)北向通道中的东向失准角φE、北向速度δVN和纬度误差δL都以地球自转为周期(1d)振荡发散,它们主要由地球自转误差中的Y轴分量δω造成。δω除了引起东向失准角φE外,还会导致天向失准角φU,两者都受到地球旋转周期RZ(-θE)的调制作用。
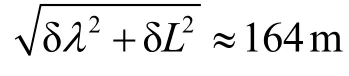
在惯性导航算法中若将地球自转角速度修正为:
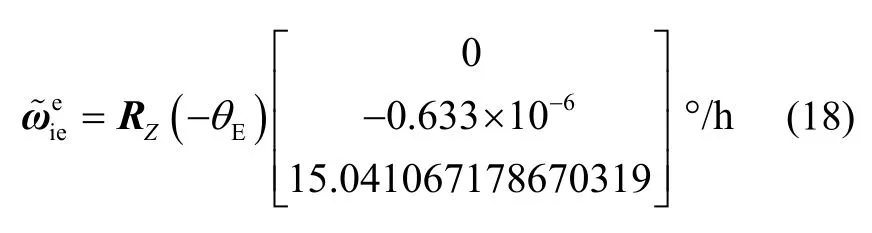
式(18)表示对地球自转角速度的X轴和Y轴补偿岁差的影响,重做纯惯导解算仿真,结果如图3所示。与图2相比,图3在100 d时的纬度误差δL从140 m降低到了50 m(降低了60%以上),基本消除了岁差的影响,剩余的纬度误差δL主要是由章动导致的。除北向通道外,天向失准角φU误差也减小了不少,从4.4 ″下降到了1.5 ″。这说明,进行地球自转角速度的岁差修正对长航时导航精度的提升效果还是比较明显的。

图3 100天纯惯导误差(岁差修正后)Fig.3 Inertial navigation errors within 100 days (after precession correction)
显然,在实时惯导应用过程中,如果能够预测dUT1(或LOD)的变化趋势[13],对该趋势进行建模和补偿,将有助于减小纯惯导解算的经度误差,针对该问题就不再仿真赘述了。由于极移的周期较长(约为一年),根据当前极移值或仅需进行简单预测,容易补偿大部分极移误差的影响。
4 结 论
根据IAU岁差章动模型和EOP日长变化数据,本文求解获得了精确的地球自转角速度数值,它在垂直于地球自转轴的方向上存在1×10-6°/h量级的角速率波动。长航时纯惯性导航仿真结果显示,使用传统的地球自转角速度模型,会引起0.1 n mile/100 d的导航定位误差。因此,在高精度惯导系统中,比如当陀螺漂移误差小于1×10-5°/h时,有必要考虑采用本文提出的地球自转角速度建模方法,以减小导航环境因素误差的影响。
致谢:感谢西安理工大学的翁浚提供的帮助。
