带全局-局部最优步长比例因子的布谷鸟搜索算法

梁毛毛,肖 文,王李进,钟一文

(1.福建农林大学计算机与信息学院,福建 福州 350002) (2.福建农林大学智慧农林福建省高校重点实验室,福建 福州 350002)

元启发式算法是一种基于经验的非确定性算法,在处理结构不明确、缺少条件或大规模的优化问题上具有优势,在环形电感建模[1]、优化配电网网架[2]和储能配置[3]、求取自由曲面最大主曲率[4]等方面有广泛应用. 布谷鸟搜索(cuckoo search,CS)算法[5-6]是其中的一种自然启发式算法,起源于布谷鸟寻巢产卵并让其他鸟为其孵卵的行为. CS算法利用Lévy Flights随机走动和Biased随机走动迭代地发现新的个体.

为了得到性能更好的CS算法,部分学者结合了其他优化方法. Wang等[7]将和声搜索与CS算法混合,提出HS/CS算法;Rosli等[8]结合正余弦算法,提出一种混合布谷鸟搜索算法(HMSCACSA);Shehab等[9-10]不仅提出与爬山算法结合的稳定的布谷鸟搜索算法(CSAHS),且引入蝙蝠算法来求解全局数值优化;还有研究[11-12]将合作协同进化框架、单位置继承等技术引入CS算法. 部分学者致力于改进Lévy Flights和Biased随机走动的过程. Wang等[13]提出采用均匀分布的随机数动态设置步长因子的布谷鸟搜索算法(VCS);王李进等[14-15]分别采用逐维搜索和正交交叉操作加强了Biased随机走动搜索效率. 为了改善CS算法在求解复杂问题时的性能退化,Salgotra等[16]提出了自适应的CS算法;Wei等[17]提出一种基于柯西分布和莱默平均值更新Biased随机走动中的变异算子的方法,并命名为CSAPC;Wang等[18]利用指数曲线模拟步长因子和发现概率的变化趋势,提出基于指数函数的CS算法;Chen等[19]在Lévy Flights随机走动中采用基于最优解逐维更新个体的策略,提出逐维增强的CS算法.

Lévy Flights随机走动中的步长比例因子是CS算法中的重要控制参数,能够影响算法的搜索能力并调整算法的收敛速度. 在标准的CS算法中,步长比例因子为固定的常数,算法存在收敛速度慢、求精能力不足等缺陷,因而有很多学者围绕该点展开了改进. 林要华等[20]引入贝塔分布动态设置步长因子;Walton等[21]提出利用迭代次数更新步长因子;Valian等[22]使用迭代次数构建指数函数更新步长因子;Layeb等[23]将量子计算的概念应用在步长因子上. 然而,以上优化步长比例因子的研究均未利用到种群中个体本身的条件. 本文采用一种基于个体适应值的步长因子更新策略,提出带全局-局部最优步长比例因子的布谷鸟搜索算法(cuckoo search algorithm with global-local best scaling factor,GLbestCS).

从仿真实验的结果可以看出,GLbestCS可行且能有效改善CS算法的求精能力和收敛速度,其性能总体上比采用固定常数、均匀分布的随机数以及贝塔分布的随机数步长因子的CS算法更优.

1 布谷鸟算法

2009年,Yang等[5-6]提出CS算法. 初始化种群后,CS算法迭代执行Lévy Flights随机走动和Biased随机走动来搜索新个体. 每次随机走动结束,CS算法都会以适应值为依据贪婪地选择较优个体来更新种群.

Lévy Flights是一种从Lévy分布中获取步长的随机走动,主要作用为全局搜索. 在第G代(G>0),Lévy Flights随机走动可用以下公式表示:

(1)

式中,α0为比例步长因子(通常α0=0.01);Xbest表示目前发现的最优个体;β为常数,在CS算法中通常设置为1.5;μ和ν是随机数,服从均值为0、标准差为1的正态分布;Γ是一个伽马(Gama)函数,

(2)

Biased随机走动是一个局部随机游走过程,主要作用为局部开发,以当前个体为基础,根据在搜索池中随机选择的两个个体产生新个体. Biased随机走动可用下式表示:

(3)

式中,⊗为乘法算子;m和n为随机下标;pa为发现概率,其值为小数.

2 带全局-局部最优步长比例因子的布谷鸟搜索(GLbestCS)算法

2.1 全局-局部最优步长比例因子

步长比例因子α0是CS算法中的重要参数之一.当其值较大时,全局搜索能力较强,收敛速度较快,但算法的求精能力差;当其值较小时,局部搜索能力增强,收敛速度变慢,易陷入局部最优的情况.因此,如何设定步长比例因子决定了能否实现全局与局部搜索之间的有效平衡.

参考文献[24],本文引入种群中个体的信息更新CS算法中的步长比例因子,增加一个全局最优适应值和个体最优适应值的比值来调节算法的收敛度速度和求精能力之间的平衡,最终得到步长比例因子公式为:

(4)

式中,α0i是第i代的步长比例因子;fgbest代表全局最优适应值;fpi代表该个体的最优适应值;k为常数.当个体靠近最优情况,fgbest/fpi减小,算法的寻优精度增强;当个体远离最优情况,fgbest/fpi增大,算法的全局搜索速度加快.文献[10]中采用均匀分布的随机数动态设置步长因子,服从[0,1]均匀分布的均值为0.5.故在后续实验中令k=0.5,即:

(5)

2.2 GLbestCS算法

与CS算法相比,GLbestCS算法未引入新的操作,仅用适应值更新步长比例因子α0i,因此认为GLbestCS与CS时间复杂度相近. 同时,GLbestCS算法的性能显著更优,即更有效率. 因此,本文认为,GLbestCS 算法未增加算法整体的时间复杂度.

3 仿真结果

本文利用测试函数来评估GLbestCS算法的性能. 选择Noman等[25]提出的20个基准函数,在每个测试函数上独立运行25次. 为了使误差最小化,限制最大适应值评估次数(MaxFES)为10 000×D(D为函数维度);发现概率pa的值取0.25;当D=10时,种群规模NP为30;当D取其他值时,令NP=D.

3.1 性能分析

表1所列为当D=30时,CS和GLbestCS算法在所有测试函数上的表现. “AVGEr±SDEr”代表平均适应值误差和标准方差. 最后一行是基于α=0.05的Wilcoxon符号秩检验的统计结果,“+”代表GLbestCS算法的表现显著优于CS算法,“-”相反,“=”为两者不存在明显差异.

由表1可以看出,在函数Fsph、Fros、Fack、Fgrw、Fras、Fsch、Fsal、Fwht、Fpn1、Fpn2、F1、F2、F4、F5、F6、F9、F10上,GLbestCS算法的表现优于CS算法;在函数F3、F7上则相反;仅在函数F8上两者的表现近似. 同时,GLbestCS 算法在14个函数上表现更优,在5个函数上与CS算法近似,仅在1个函数上略差. 且GLbestCS算法在函数Fgrw上能够取得全局最优解. 图1展示了CS和GLbestCS算法在测试函数中的一些有代表性的收敛过程. 可以看出,GLbestCS算法在前期有更快的收敛速度、在后期有更强的求精能力.

因此,可以认为,用全局-局部最优适应值动态设置步长比例因子是可行的,且能够改善CS算法的性能.

图1 CS和GLbestCS的收敛曲线Fig.1 The convergence curves of CS and GLbestCS

3.2 维数变化对算法性能影响分析

表2比较了CS和GLbestCS在不同维度的运行结果,可以看出GLbestCS算法的性能基本上稳定地优于CS算法.

表2 CS和GLbestCS求解测试函数的平均适应值误差(D=10 and D=50)Table 2 Average fitness error obtained by CS and GLbestCS for benchmark functions(D=10 and D=50)

3.3 与其他改进的CS算法比较分析

表3所列为VCS、BetaCS和GLbestCS算法在测试函数上的表现. 表4的方法是Wilcoxon配对秩和检验[26],其中“R+”表示GLbestCS算法获得的平均适应值误差排序总和比另一算法的更好,“R-”相反. 表5给出了Friedman检验[27]结果. 综合而言,GLbestCS算法的性能优于VCS和BetaCS算法.

表3 VCS、BetaCS和GLbestCS求解测试函数的平均适应值误差(D=30)Table 3 Average fitness error obtained by VCS,BetaCS and GLbestCS for benchmark functions(D=30)

表4 VCS、BetaCS和GLbestCS的Wilcoxon配对秩和检验(D=30)Table 4 Wilcoxon matched-pairs signed-rank test for VCS,BetaCS and GLbestCS(D=30)

表5 3个算法求解测试函数的平均Friedman检验秩(D=30)Table 5 Average ranking of three algorithms by the Friedman test for 20 functions(D=30)

3.4 对k值的讨论

表6给出当k取值不同时GLbestCS算法在测试函数上取得的结果.

表6 GLbestCS求解测试函数的平均适应值误差(k=0.5,k=1 and k=1.1)Table 6 Average fitness error obtained by GLbestCS for benchmark functions(k=0.5,k=1 and k=1.1)

续表6Table 6 continued

可以看出,当k=0.5和k=1.1时算法的性能近似,均优于k=1.0时.在表7中,部分情况下k=1.1的算法性能略优.由于个体靠近全局最优时,方程(5)后半部分的比值变大,α0i的值逐渐变小.当k=0.5时,若当前个体达到全局最优,即fgbest/fpi=1时,α0i取得最小值-0.5,Lévy Flights随机游走的方向改变,算法会继续反向搜索. 故本文最终选择了较优的k=0.5.

表7 GLbestCS求解测试函数的平均Friedman检验秩(D=30)Table 7 Average ranking of GLbestCS by the Friedman test for 20 functions(D=30)

3.5 在其他算法上应用的讨论

将本文所提算法应用于文献[28]提出的CCS算法,命名为GLbestCCS算法. 表8和表9列出了CCS和GLbestCCS算法在D=30时的运行结果. 可以看出,GLbestCCS算法的性能显著优于CCS算法.

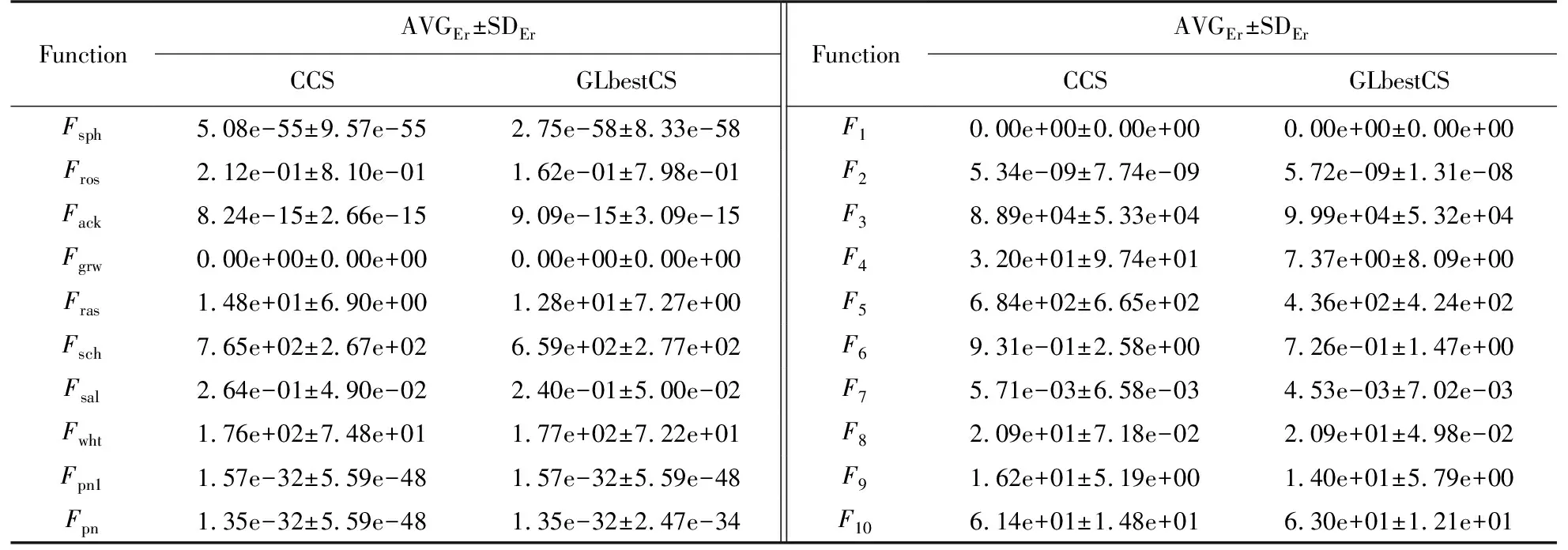
表8 CCS和GLbestCCS求解测试函数的平均适应值误差(D=30)Table 8 Average fitness error obtained by CCS and GLbestCCS for benchmark functions(D=30)

表9 CCS和GLbestCCS的Wilcoxon配对秩和检验(D=30)Table 9 Wilcoxon matched-pairs signed-rank test for CCS and GLbestCCS(D=30)

4 结论

本文采用最优适应值动态设置步长比例因子,并提出一种带全局-局部最优步长比例因子的布谷鸟搜索算法GLbestCS. 实验结果证明,GLbestCS算法可有效地改善CS算法的性能. 当问题规模发生变化,GLbestCS算法仍然稳定地优于CS算法. 将该策略应用于其他改进的CS算法,结果表明这种优化仍然有效.