基于天牛群-反馈神经网络的绞线串扰预估
2022-07-06周建明张海龙颜伟刘兴发
周建明,张海龙,赵 阳,颜伟,刘兴发
(1.南京师范大学南瑞电气与自动化学院,江苏 南京 210023) (2.中国电力科学研究院武汉分院电网环境保护国家重点实验室,湖北 武汉 430074)
随着电力设备的集约化、高频化程度的不断提高,传输线之间的串扰问题日益严重,已成为一个不能忽视的问题[1-2]. 所谓串扰是指激励线上的电流和电压产生的电磁场将影响相邻的传输线,并在它们的端点处产生感应信号,是一种非意图的耦合现象[3-4]. 对于平行多导体传输线(multiconductor transmission lines,MTL)结构,串扰值可通过直接求解传输线方程得到[5].
串扰求解方法可分为时域法和频域法两种. 时域法中,Tesche[6]推导了双导体传输线的时域Baum-Liu-Tesche(BLT)方程来求解传输线终端响应,与链参数矩阵法不同的是,BLT方程用散射参数来表征管道,将网络中所有管道的管道特性和网络中所有节点的散射矩阵表达式进行归类以得总特性表达式. 邵志江等[7-8]以单线、双绞线、三绞线以及单层屏蔽线、双层屏蔽线建立了多种串扰模型,分析了它们的近端和远端时域串扰. 时域有限差分法(finite difference time domain,FDTD),由于计算简单快速、便于得到激励信号下传输线任意空间、时间处的信号波形,应用最为广泛. 但FDTD的缺点在于网格划分受稳定性和数值色散的条件限定[9-10].
频域法主要起源于Paul[11]的链参数理论,他将传输线等价成2n端口网络,以导纳参数或阻抗参数表征管道,通过传输链参数矩阵简单轻易地将各种网络结构连接起来,结合戴维南和诺顿等值约束条件可直接推导出传输线近端和远端串扰电压和电流的频域解[12]. 但绞线的横截面不固定,扭转角度发生变化,传输线方程中的PUL寄生参数是一变量,传统方法已不能直接用于求解串扰. 包贵浩等[13]建立了非均匀螺距双绞线的频域串扰模型,得到感性耦合和螺距误差的关系,并基于螺距误差的概率密度函数,分析了任意双绞线串扰的统计特性. Cannas等[14-15]提出将双绞线进行分段级联,一部分PUL寄生参数通过数值计算得到,并作为训练样本,其余通过BP神经网络预测得到,分析双绞线的频域串扰波形. 传统的BP神经网络存在着迭代误差大,易于陷入极小值等缺陷,可应用性一般.
1 多导体传输线的频域分析
在多导体传输线结构的频域分析中,电路结构尺寸不满足远小于电磁波波长这一条件,此时需将传输线视为具有沿着轴向方向上的分布参数结构,即该导体电路结构属于电大尺寸. 同时,假设围绕着导体的电磁场具有横向结构,即空间电场和磁场相对于轴线方向是横向或者正交的. 在横向电磁场结构下,多导体传输线等效电路可由图1表示.
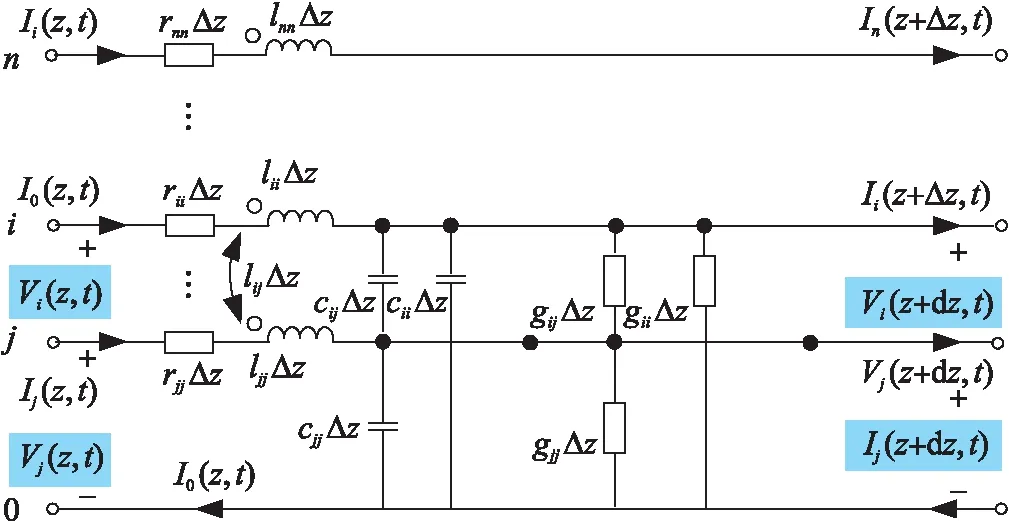
图1 多导体传输线分布参数电路Fig.1 MTL distributed parameter circuit
图中rij,lij,cij和gij分别代表PUL电阻R(z),电感L(z),电容C(z)和电导G(z)寄生参数矩阵中的元素.其中,i,j=1,2,…,n.本文假定各参数与频率无关,由参数矩阵和端口电压、电流一起构成传输线方程,
(1)
(2)
式中,V(z,t)和I(z,t)是传输线上某一位置、时刻处的电压和电流向量.PUL参数矩阵随轴向位置z发生改变,默认对传输线进行分段后,每一小段可将其视为平行传输线处理.接下来,利用频域链参数的方法对若干小段级联而成的传输线进行求解.首先,定义传输线的阻抗和导纳矩阵分别为:Z=R+jωL,Y=G+jωC.对其乘积进行特征值分解
(3)
式中,γ为特征值.则传输线的特征阻抗矩阵及其逆矩阵为:
(4)
(5)
由此,传输线两端向量电压和电流间的关系由链参数矩阵表征为
(6)
式中,
(7)
(8)
(9)
(10)
将每一分段处的链参数进行如图2所示的级联,依据公式(12)由负载端向源端相乘,即可得到完整的传输线链参数矩阵.
(11)
(12)
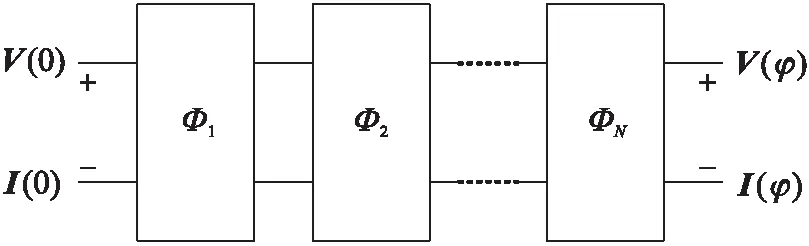
图2 链参数级联法示意图Fig.2 Schematic diagram of chain parameter cascade method
结合边界广义戴维南等值条件(12),代入式(6)展开求解,将式(12)代入式(6),
(13)
由式(13)得到终端电流解I(0)和I(φ),进一步从终端关系中得到V(0)和V(φ).
当激励源幅值为1 V时,定义N和F分别为近端串扰(near end crosstalk,NEXT)和远端串扰(far end crosstalk,FEXT),
(14)
其中i代表传输线编号.
2 BSO算法的提出与优化流程
根据前文可以得到绞线串扰求解的核心是获得每一分段处的PUL参数矩阵. 因此,在之前研究的基础上,我们提出利用BP神经网络预测参数矩阵,并通过BSO算法优化神经网络的权值. BSO算法是将之前的BAS算法与粒子群结合而来,在之前的工作中我们发现,BAS算法在处理高维数据时结果不能令人满意,且迭代结果在很大程度上取决于随机生成的初始位置. 因此,将BAS算法中的单体天牛寻优扩展为群体寻优,每一只天牛能够互相分享信息,且它们的移动方向和距离取决于触须所感应到的信息. 将该算法用于BP神经网络中,天牛的位置即为神经网络的权值,优化目标为神经网络误差. 迭代完成后,天牛最终位置即为最优权重.
2.1 BSO算法流程
在BP神经网络的经典三层结构中,输入层定义为扭转角度,输出层定义为RLCG参数上三角矩阵排为一列,对于三绞线,即24行. 隐含层层数为
hidden=(input+output)1/2+2.
(15)
式中,hidden为隐含层,input为输入层,output为输出层. BSO算法优化权值的基本流程如图3所示. BSO算法的具体优化步骤如下.
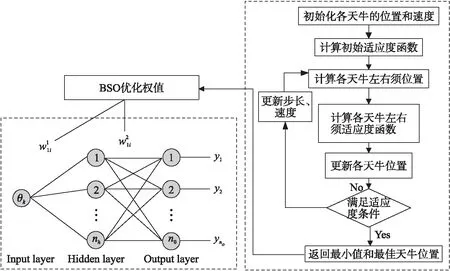
图3 BSO算法优化权值流程图Fig.3 BSO algorithm optimization weight flow chart
步骤1. 在S维空间中随机生成一组n个个体的天牛群,B=(B1,B2,…,Bn),其中第i个天牛Bi代表一个向量,即一个优化目标的潜在解,Bi=(bi1,bi2,…,biS).另外,定义天牛的运动速度Vi=(Vi1,Vi2,…,ViS),为了加快寻优速度,我们还规定了天牛个体和群体的速度阈值范围Ui=(Ui1,Ui2,…,UiS)和Ug=(Ug1,Ug2,…,UgS).
步骤2.给出天牛位置和速度的迭代公式
(16)
式中,s=1,2,…,S;i=1,2,…,n;k是当前迭代次数,δis是天牛位置步进距离,λ是一常数.
(17)
式中,ω是BSO算法的一个初始权重,c1、c2为常数,r1、r2是[0,1]之间的随机数.
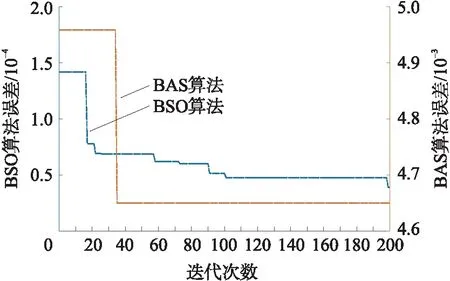
图4 BSO和BAS迭代误差对比Fig.4 Comparison of iteration errors between BSO and BAS
步骤3.确定天牛移动距离和方向
(18)

(19)
d是天牛左右触须之间的距离,即天牛通过左右触须接收信号,并朝着信号强的方向进行移动. 迭代结束后,天牛群中感应信号最强烈的天牛位置即为优化之后的神经网络权值.
2.2 迭代误差对比
分别用BSO算法和BAS算法对神经网络的权值进行优化,获得其迭代误差如图4所示.
由图4可知,BAS算法在200次迭代过程中只更新了1次位置,而BSO算法更新了7次. 且BAS算法最终误差为4.65e-3,BSO算法为3.90e-5,精度提高近120倍,由此证明对于优化算法作出的改进效果显著.
3 数值仿真验证与对比
首先建立图5所示的三绞线模型. 模型的具体参数见表1.
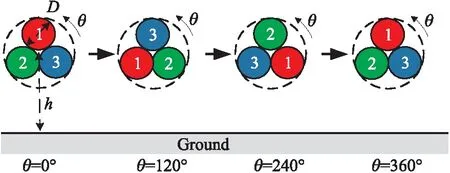
图5 三绞线截面模型Fig.5 Triple twisted wires cross-section model

表1 模型参数Table 1 Model parameters
借助于ANSYS软件提取了一组PUL参数矩阵作为神经网络训练样本,其余扭转角度下参数矩阵由上文中BSO-BP神经网络预测得到. 由于三绞线为循环对称结构,因此,我们只需获得图5中0°~120°内的参数矩阵,120°~240°和240°~360°内的参数矩阵分别由矩阵一左乘T1,右乘T2矩阵实现线芯换位得到,其中:
(20)
(21)
接着,分别对基于BSO-BP算法、BAS-BP算法和BP算法预测的PUL寄生参数进行串扰求解,并在CST cable studio搭建上述模型,均设定200个频率点,其中激励源为1 V正弦信号,端接50 Ω电阻,将仿真结果作为对比值.
由于三绞线中除1号激励线外,2号、3号受扰线相对称,其近端、远端串扰值相等,因此只需分析单根受扰线结果. 结果表明,本文所提出的BSO-BP算法对于绞线串扰的的预估值与仿真波形大小、趋势最为吻合,验证了方法的有效性. 在表2中也给出了3种方法在高、中、低频下与仿真值的相对平均误差.

表2 串扰相对平均误差对比Table 2 Crosstalk relative average error comparison
可见,在3个频段内,BSO算法所优化过的BP神经网络具有最高的预估精度,尤其在低频段. 中高频段内由于存在过多谐振点,导致预估精度有一定下降.
4 结论
本文给出了多导体传输线频域形式下的解析解,针对绞线单位长度寄生参数矩阵随扭转角度变化的特点,选择利用链参数级联的方法求解. 提出了利用BSO优化算法与BP神经网络相结合的方式预测参数矩阵,通过将神经网络误差定义为优化目标的形式提高预测精度. 并将BSO算法的迭代误差与之前研究中的BAS算法迭代误差进行比较,结果表明采用群体寻优之后,迭代误差可减小约120倍. 最后,分别将BSO-BP算法、BAS-BP算法和BP算法下预测的参数矩阵代入传输线方程进行串扰求解. 结果表明,BSO-BP算法吻合度最高,在高、中、低频下的串扰预估误差相较于初始的BP算法分别提高了257、80.5、50倍. 该方法的提出对于电力设备进行信号完整性设计、电磁干扰评估具有重要意义.
