基于分布鲁棒优化的社区型能源系统低碳经济调度
2022-07-06孙旺青刘晓峰季振亚陈雪颖
孙旺青,刘晓峰,季振亚,柏 颖,陈雪颖
(南京师范大学南瑞电气与自动化学院,江苏 南京 210023)
为了应对全球气候变暖问题,我国提出了“3060目标”,即二氧化碳排放力争2030年前达到峰值,努力争取2060年前实现碳中和. 合理处理可再生能源出力的不确定性,实现能源系统的低碳调度是实现我国“碳达峰”“碳中和”目标的关键[1].
当前,针对能源系统不确定性的处理方法包括随机优化和鲁棒优化. 随机优化需要获得随机变量的精确的概率信息,难以在工程中直接应用,而鲁棒优化不需要随机变量的概率信息,以波动范围表征变量的不确定性,通过完成最恶劣场景下的调度提高系统的鲁棒性. 文献[2]构建了多微网两阶段鲁棒优化模型,有效减少了微网与配电网间的互动次数,但调度结果过于保守,不利于新能源消纳率的提高. 分布鲁棒优化是一种新兴的解决能源系统不确定性的方法,通过寻找随机变量的最恶劣概率分布求解优化问题,因此分布鲁棒优化可降低调度结果的保守性[3]. 文献[4-5]采用分布鲁棒优化求解能源系统中的不确定优化问题,结果表明分布鲁棒优化比随机优化更稳健、比鲁棒优化更经济. 此外,也有学者对能源系统多主体之间的利益关系进行了研究,文献[6]从合作博弈角度出发,采用鲁棒优化求解考虑不确定性的微网调度问题. 文献[7]从多主体博弈角度出发,应用前景理论处理用户参与电力交易时的不确定性,但是该方法也需要随机变量的概率分布,难以直接应用.
目前关于分布鲁棒优化的研究均属于单主体决策的不确定性问题,缺少针对多主体的分布鲁棒优化的研究[8]. 事实上,一个能源系统中有多个决策主体,在实时电价的影响下,各决策主体的调度策略会受彼此影响,这是一个可由博弈理论描述的动态决策过程[9]. 鉴于此,本文以社区型能源系统为研究对象,以提高调度策略的鲁棒性、低碳性为目标,提出了一种非合作博弈模式下的分布鲁棒博弈调度方法,并利用线性决策理论及对偶原理对模型进行求解.
1 社区型能源系统模型
建立系统场景如图1所示,一个调度周期包含T个时段,社区型能源系统包含N个社区,各社区均配备燃烧后捕集型的碳捕集设备,如图1中虚线所示,碳捕集机组运行时会封存部分二氧化碳.区域电网调度中心负责用户负荷、实时电价的收集与发布.

图1 社区型能源系统场景图Fig.1 A conceptualized structure of energy system in communities
1.1 社区n日前调度模型
日前调度是基于风电功率的预测出力信息完成优化调度,社区n日前调度的目标函数可表示为:
(1)
(2)
(3)
(4)
(5)
(6)
(7)

(8)
(9)
(10)
(11)
(12)
(13)
(14)

1.2 社区n日内调度模型
分布鲁棒优化会寻找出社区n日内风电功率的最恶劣概率分布并完成调度,从而降低不确定性对系统造成的冲击.社区n日内调度的目标函数为:
(15)
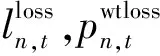
(16)
(17)
2 各社区间分布鲁棒博弈模型
2.1 风电功率的模糊集
分布鲁棒优化采用区间形式刻画随机变量的波动范围,风电功率波动的不确定集为
(18)

(19)
(20)
针对引入的辅助变量,同样也应对其边界条件进行刻画,不确定集(18)改写为:
(21)

2.2 分布鲁棒调度模型转化
社区n的日前调度模型的矩阵形式可表示为
mincTx,
(22)
s.t.Ax≤b.
(23)

(24)
s.t.Mx+Ny≤h(u).
(25)

h(u)=h0+huu.
(26)
式中,h0为常系数向量;hu为与随机变量u有关的列向量.n日内调度的决策变量同时受随机变量和辅助变量的影响,本文采用线性决策规则逼近决策变量的取值[12-13],社区n日内调度的决策变量y改写为:
y(u,ω)=y0+yuu+yωω.
(27)
式中,y0为常系数向量;yu为与随机变量u有关的列向量;yω为与随机变量ω有关的列向量.不确定集(21)的矩阵形式可表示为:
(28)
本文所提分布鲁棒优化模型包括式(20),(22)~(25)和(28),该模型是无限维的NP-Hard问题,难以直接求解.本文首先将无限维问题转化为半无限规划模型:
(29)
式中,式(29)为式(24)内层的sup(·)问题;f(u,ω)为随机变量u和ω的概率测度;式(30)对应模糊集(20)中第一行约束;式(31)对应模糊集(20)中第二行约束式(32)对应模糊集(20)中第三行约束.利用对偶原理将式(29)~(33)转化为有限维优化问题:
(34)
式中,α,β,γ为对偶变量,依次对应式(30)~(32).至此,概率信息已包含到模型(34)~(36)中,结合日前调度阶段表达式(22)~(23),完整的两阶段分布鲁棒优化模型可转换为如下形式:
(37)
(42)
式中,θ为不确定集(28)对应式(39)的对偶变量;λ为不确定集(28)对应式(40)的对偶变量.

图2 社区间分布鲁棒博弈流程图Fig.2 Flow chart of distributionally robust game
2.3 分布鲁棒博弈流程
由于能源系统内各社区的调度成本受到实时电价的影响,且实时电价的数值取决于各时刻能源系统总用能需求.因此各社区的决策行为是一个相互影响的动态决策过程,本文用非合作博弈将该动态决策过程描述如下:
(2)策略集:各社区调度策略;
(3)收益函数:社区n参与博弈的收益Pn,
(51)

(52)

3 案例分析
为了验证社区型能源系统分布鲁棒博弈模型的有效性,以N=3的社区构成的能源系统为例,根据负荷水平将一天分为3个时段,分别是低谷时段(0:00—6:00,22:00—次日4:00)、平时段(6:00—17:00)和高峰时段(17:00—22:00),低谷时段参数a(t)和b(t)为0.2和53,平时段为0.3和111,高峰时段为0.4和179. 考虑到各社区在地理位置上邻近,风力资源条件相近,假设各社区配置了相同容量的储能系统且风电功率相同. 同时假设风电功率的波动符合均值为0,标准差为0.15倍预测值的正态分布[14],采用蒙特卡洛方法随机生成5 000组出力数据作为风电功率波动的测试场景. 图3给出了各社区的风电出力期望值及波动区间,图4给出了各社区的负荷需求.

图3 风电出力期望值Fig.3 Expected value of wind power output
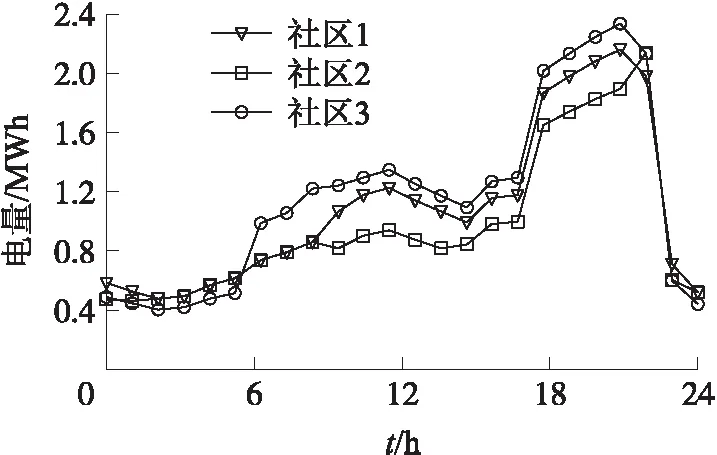
图4 各社区负荷需求Fig.4 Load demand of each community
3.1 调度结果
基于以上参数配置可以对各社区完成分布鲁棒博弈调度,图5为各社区在非合作博弈模式下分布鲁棒优化的调度结果,从图中可以看出,各社区向区域电网的购电行为主要集中在低谷时段,此时的电价较低,有效降低了各社区的购电费用,并且未出现某一时段所有社区集中购电、对区域电网造成冲击的行为. 各社区所配备的发电机组在低谷时段以较低功率运行,此时的电价较低廉且风电资源充足,而在平时段和高峰时段发电机组均以较高功率运行,因为此时的电价较高昂且风电资源相对稀缺,各社区通过自身的发电机组可以进一步降低社区的运行费用. 此外,各社区储能系统的储能行为分布在低谷时段,储能系统集中在高峰时段为社区负荷供能以降低购电费用.

图5 各社区分布鲁棒博弈调度结果Fig.5 Energy scheduling result of each community under distributionally robust game
3.2 分布鲁棒算法性能分析
表1给出了分布信息数量与优化结果之间的关系. 其中,成本是指风电功率处于最恶劣分布时各社区调度成本的期望值;总成本变化率指相较于上一组总成本数值的变化情况,如分布信息数量为2时的成本变化率是指相较于分布信息数量为1时的成本变化情况. 从表中可以看出,随着考虑的分布信息数量的增加,本文搭建的分布鲁棒优化模型对风电功率的描述越来越接近可能的真实情况,极端情况的权重会下降,因此模型保守度会降低,社区运行成本也会得到削减. 但是运行成本不会一直降低,当考虑了3个分布信息时,分布鲁棒优化模型已经可以较准确地描述风电功率的概率信息,故再增加分布信息,并不会对结果产生较大改变.

表1 分布信息数量与成本期望值之间关系Table 1 The relationship between the amount of moment information and expectation of production costs
此外,样本大小也会对调度结果产生较大影响,因为不同大小的样本所提供的分布信息也略有不同. 表2给出了50~5 000个样本数据时的调度结果(考虑到实际场景中,历史数据数量较匮乏,且根据表1 可知,只选取1个分布信息时的调度结果也较为可信,故此处选取的分布信息数量为1). 从表1可以看出,随着样本数量的增加,得到的概率分布更接近于真实值,日前调度阶段可以得到考虑更全面的调度策略,所以在日内调度阶段大大降低了运行风险及平衡费用. 同样,由于更多场景在日前调度阶段被考虑,所以日内调度阶段失负荷量也进一步被降低.

表2 样本大小与优化结果之间关系Table 2 The relationship between sample size and optimization results

图6 不同样本大小对成本的影响Fig.6 The impact of sample size on cost
图6以50组样本时的各项费用作为基准,更清晰地给出了不同样本大小时社区成本的变化情况. 可以看出随着样本大小的增大,日前成本缓慢上升,而日内成本的下降速率较大,这是因为风电功率被描述的越准确,日内调度阶段所面临的风险就越小,因此日内调度的成本会大幅降低. 此外,从图中同样可以看出,随着样本大小达到一定程度,系统总成本便不会再降低,这是因为调度策略已经考虑了绝大部分可能性,所以再继续增加样本不会对结果造成较大影响.
3.3 方案对比
为了验证本文所提出的分布鲁棒优化模型的有效性及低碳性,通过3个场景进行对比分析.
场景1:不考虑碳捕集设备,采用分布鲁棒优化;
场景2:考虑碳捕集设备,采用分布鲁棒优化;
场景3:考虑碳捕集设备,采用鲁棒优化.
碳捕集设备的效益分析如表3所示,其中发电总量是指净发电量和用于碳捕集设备的电量之和,机组总成本是指发电机组运行的总成本(包括维持碳捕集设备运行的成本). 对比场景1和场景2可以发现,虽然加入碳捕集设备后,机组发电费会有所提高(约25%),但通过碳捕集设备可以大大降低系统的排碳量(约62%),在碳市场降低支付费用,因此场景2机组的总成本依然比场景1低(约6%). 上述结果表明,碳捕集设备可以提高社区系统的低碳性与经济性.

表3 碳捕集设备的效益分析Table 3 Cost-benefit analysis of carbon capture equipment
表4给出了场景2和场景3的对比,分析了鲁棒优化和分布鲁棒优化的风险偏好. 从表中可以看出,鲁棒优化的日前调度成本比分布鲁棒优化高(约22%),且平均总成本比分布鲁棒优化高(约21%),但最大日内调控成本比分布鲁棒优化低(约30%),这是因为鲁棒优化更偏向于最恶劣场景下的最优调度,而分布鲁棒优化更偏向于总体的最优化调度,这两种方法分别适用于不同类型的决策场景. 在一般情况下,考虑到极端恶劣的场景非常罕见,且一般的居民社区对电能质量没有过高的要求,故分布鲁棒优化更适合社区型能源系统.

表4 鲁棒优化和分布鲁棒优化结果对比Table 4 Comparison of robust optimization and distributed robust optimization results
表5给出了合作博弈和非合作博弈优化结果对比(均考虑碳捕集设备,均采用分布鲁棒优化方法). 可以看出,合作博弈的成本要略低于非合作博弈,这是因为采用非合作博弈时,每一个决策主体都优先考虑自身利益的最大化,而采用合作博弈时,是从整体利益最大化出发,所以会存在合作剩余. 虽然采用合作博弈时总成本略低,但是实现合作博弈的前提要形成合作联盟并确定合作剩余的分配机制,一旦联盟出现利益分配不均问题就会导致联盟瓦解. 在实际场景中,考虑到决策主体的趋利性,采用合作博弈机制的难度较大,因此非合作博弈形式的分布鲁棒模型更易实现.

表5 合作博弈和非合作博弈优化结果对比Table 5 Comparison of cooperative and non-cooperative game optimization results 元
4 结论
本文针对风电功率的不确定性以及能源系统内各社区间的动态决策过程,提出了一种考虑碳捕集的分布鲁棒博弈模型,经研究得出以下结论:
(1)所搭建的模型可以考虑风电功率的概率信息,在风电功率处于最恶劣分布时完成调度. 模型有效降低系统运行成本,在保守性和经济性之间做到了较好的平衡.
(2)应用了碳捕集机组后,虽然会额外消耗一部分电能维持运行,但可以降低社区的碳排放并在碳市场中获利,有效完成系统的低碳经济调度.
