MATLAB可视化在扭摆法测量刚体转动惯量中的应用

邱智宇 肖桂娜 苏桂锋

(上海师范大学物理系 上海 200234)

转动惯量是刚体绕轴转动时惯性量度的重要特性，在航空事业、风力发电、汽车零件等领域中起重要作用[1]．刚体的转动惯量不仅取决于构件总质量，还与其形状、质量分布以及转轴位置有关．无论刚体形状规则与否，利用扭摆法测量刚体转动惯量是精度较高的方法，是大学物理的重要必修实验，更是被广泛地应用于测量制造业零件的转动惯量[1,2]．由此，教师应重视刚体转动惯量测量的实验教学，充分展现现代信息技术时代的特征，合理利用多媒体技术实现教育现代化，调动学生对物理模型的感性认知，唤醒物理观念的理性思维；信息、编程技术与物理实验教学相结合以实现教育信息化，已经成为高校物理教育改革目前的热门研究课题和教育发展的优良趋势[5]．

本文以质量均匀物体对其几何中心转轴转动惯量的测量为例，利用MATLAB编程与Curve Fitting Tool工具，不仅能够实现转动惯量理论值可视化、实验数据拟合精确化，更能将实验过程以动画形式呈现．

1 实验工具与实验原理

1.1 实验原理

将待测物体置于螺旋弹簧载物台上，物体与螺旋弹簧同步运动．根据胡克定律，当物体在水平面上转动，转过某一角度θ后，螺旋弹簧产生的恢复力矩M为

M=-Kθ

(1)

式中，K为螺旋弹簧的扭转系数．再根据转动定理，物体的力矩M为

M=Iα

(2)

式中，I表示物体绕转轴的转动惯量，α为角加速度．物体在螺旋弹簧恢复力矩的作用下与弹簧共同绕垂直于水平面的转轴做往复运动，因此式(1)、(2)联立得

(3)

忽略轴承的摩擦力矩，由式(3)和角加速度的定义可得

(4)

令

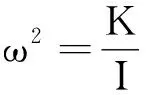
可得关于θ的二阶常微方程

(5)

由此可知置于扭摆上物体的运动具有简谐振动的特性，此方程的解为

θ=Acos(ωt+φ)

(6)

式中A为简谐振动的振幅，φ为相位角，皆由初始条件决定；ω为角速度，扭摆法过程的简谐振动周期为

(7)

所以待测刚体的转动惯量为

(8)

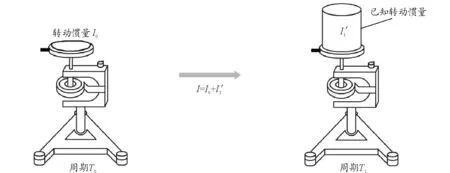
图1 扭摆法测量物体转动惯量实验原理图

(9)

式中由于T0和T1能够通过实验测量

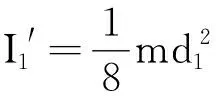
是已知量，则可得到弹簧的扭转系数K的值为

(10)

由此，只要测得待测物体随着螺旋弹簧转动的总周期，即可得到待测物体和支架的转动惯量之和[3,4]．综上所述，待测物体的转动惯量为

(11)

1.2 MATLAB介绍

MATLAB被应用于算法、数据分析与计算、数据可视化的高级计算语言和交互式环境，主要包括MATLAB和Simulink两大部分．MATLAB的主界面如图2所示.

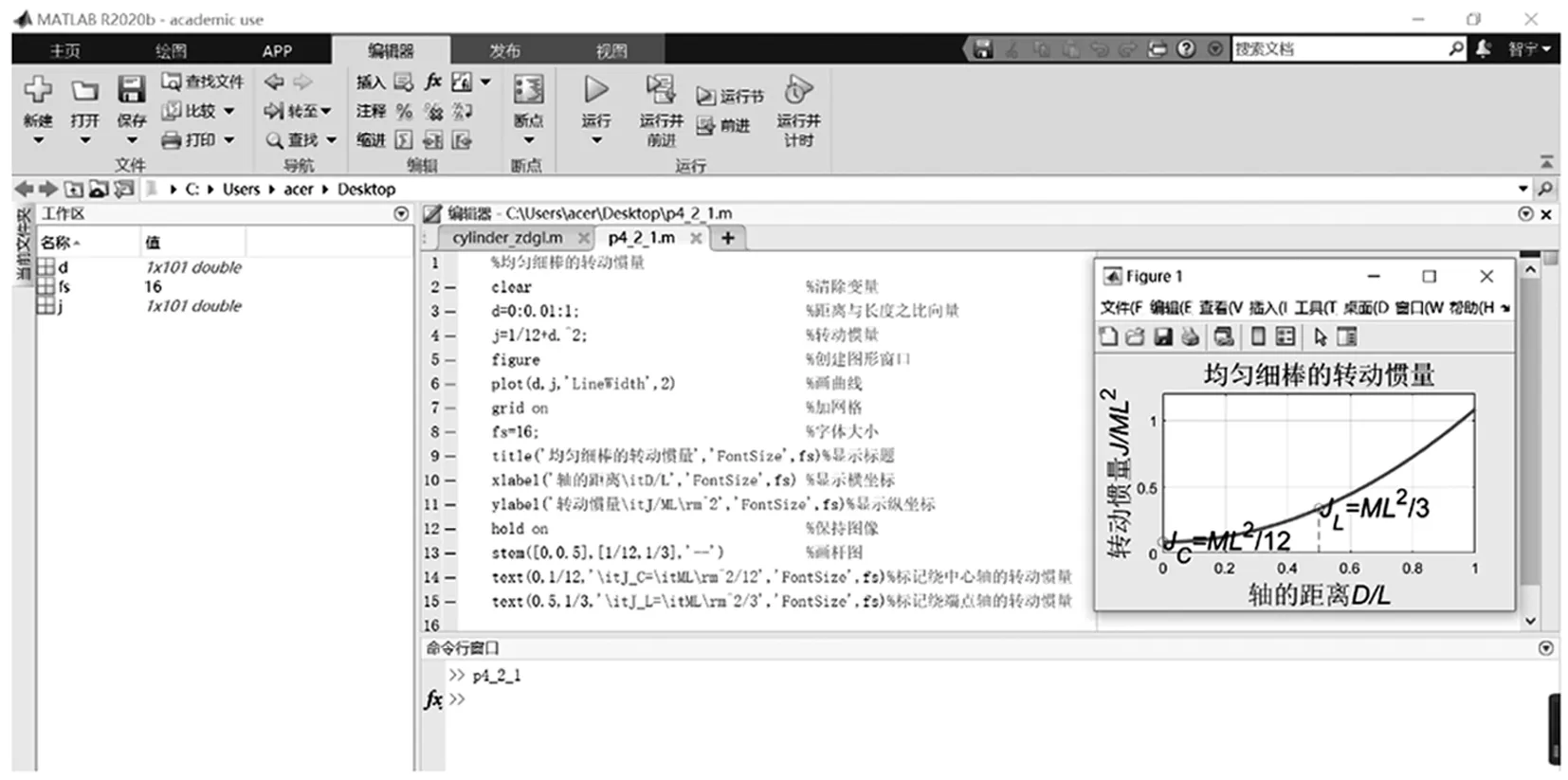
图2 MATLAB软件主界面

图2中编辑器为主体，功能为程序编入与调试，能以颜色区别代码显示的功能．运行编辑器，工作区以矩阵形式存储数据，并得出数据计算结果和绘制相关函数图像或动态图像．命令行窗口(Command Window)为主要交互式窗口，位于编辑器下方，输入指令后显示除图形以外的执行结果．命令窗口中“≫”符号为命令提示符，表示MATLAB正在处于准备状态．在命令提示符后输入命令并按回车键，MATLAB就会解释执行所输入的命令，并在命令后面给出计算结果．

MATLAB语言具有解释性，程序简洁易懂．不仅能够直接在命令行窗口输入命令，也可以在编辑器内编写应用程序，然后在MATLAB环境下对程序命令进行处理，处理的对象为矩阵或调用函数，最后返回运算结果．因此，其程序编写较易上手，可以通过直观的数学表达式实现对数据的处理．在扭摆法测量刚体转动惯量的实验中需要运用其主体与工具包Curve Fitting，前者用于实验过程动画绘制与刚体转动惯量理论值函数图像绘制；后者于工具栏中APP一栏，能直接读取实验实测中时间与位移的数据，通过傅里叶函数分析拟合，得函数表达式，可直接读出其周期值．在扭摆法测量刚体转动惯量的实验教学中， MATLAB以其语言易懂化、图像可视化、数值分析能力优异性等特点，不论是实验过程、实验理论值，还是实验测量值的函数拟合，均起到极佳的教学辅助作用．

2 实验方法

根据实验原理需要测定各类规则物体转动惯量的理论值和扭转常数K，根据规则物体转动惯量的积分计算过程，通过编辑MATLAB程序，可获得如图3所示的不同厚度的均匀圆筒和均匀球壳、不同长度均匀细杆绕中心轴或转轴，以及其他形状规则刚体的转动惯量理论值[5]．点击“工具”栏中的数据提示，便可选取理论曲线上任意一点获得单位厚度或距离细杆轴线一定距离的物体的转动惯量数值,如图3中均匀圆筒对柱体轴线的转动惯量图像中，当圆筒中空心部分半径R0与圆筒总体半径R之比为某值时，图3(a)中可直接读得数据与圆柱体的质量和半径平方的乘积即为已知质量和几何参数圆柱体的转动惯量理论值．理论值的获得不仅有助于分析实际测量物理量数据的精确程度，而且在扭摆法实验数据处理过程中具有辅助作用．

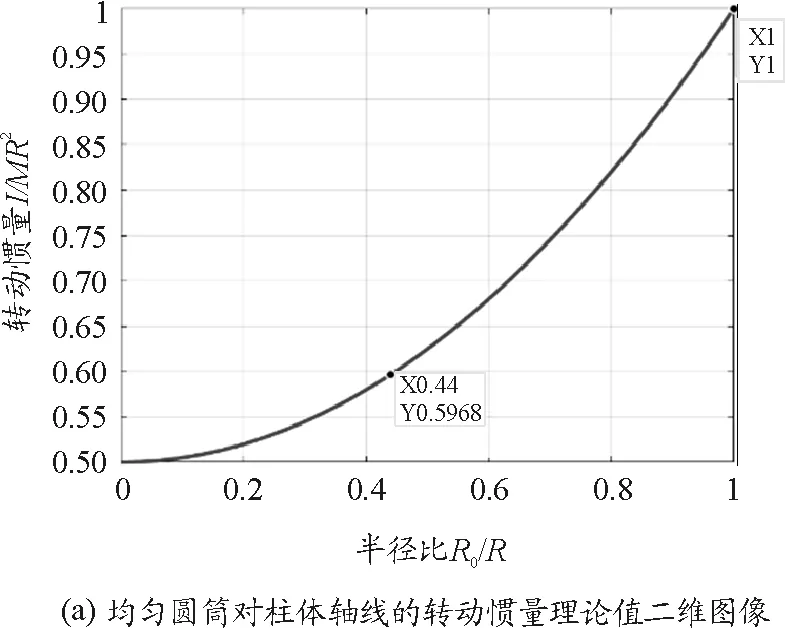
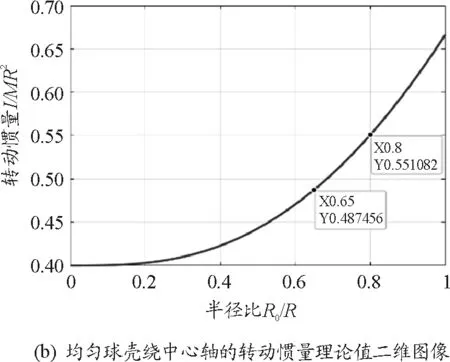
图3 规则物体转动惯量的获得

获得转动惯量的理论数据和相关实验准备工作后，利用扭摆法开始进行实物测量，第一步测量金属托盘空载时的周期．其具体步骤为：先调整扭摆底座的底角螺丝，使螺旋弹簧上侧水准仪中的气泡居中．然后，装配金属载物盘，并调整光电探头的位置，测定其摆动周期T0，测3次求平均值．扭摆法测量转动惯量的实验过程步骤存在先后顺序，且口头描述较为复杂，实验教学的过程中可通过MATLAB进行动画展示，分析每一步骤的细节与注意点．如图4所示，图中灰色圆框为金属底座的俯视图像，突出部分为挡光轴，黑色线条组成部分为光电门．

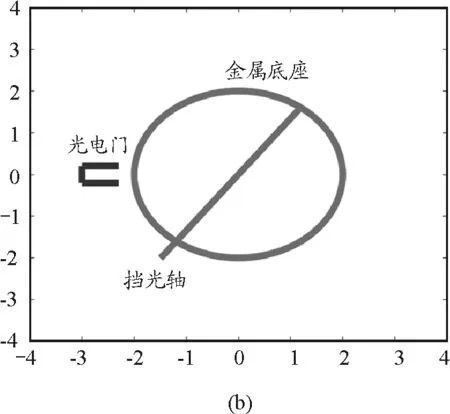
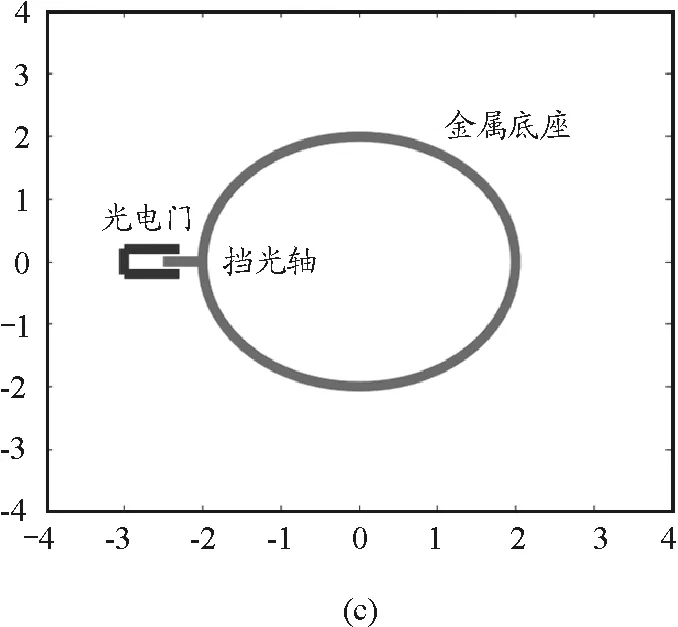
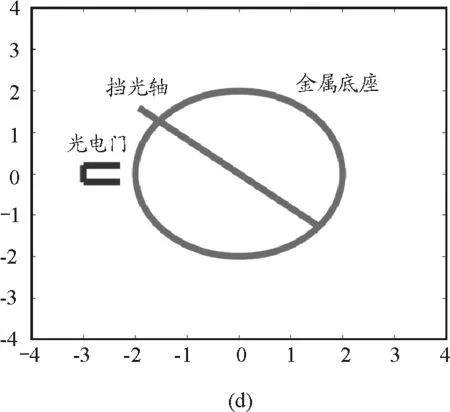
图4 扭摆法测量刚体转动惯量实验过程俯视动画关键帧图像

开始时，如图4(a)所示，需要将挡光轴与光电门所在轴线垂直，保证初始摆角相同且约为90°，此时螺旋弹簧对于转动惯量的实验测量误差影响最小[6]．释放螺旋弹簧后，载物盘随螺旋弹簧旋转(如图4所示为先顺时针旋转)，通过光电门之后，周期测定仪会记录读数，挡光轴继续向顺时针方向旋转，到达弹性限度后再沿着逆时针方向旋转，以此进行往复运动，最终周期测定仪记录挡光轴往复10次的时间，该时间除以周期测量次数后，便可得载物盘转动一次的运动周期，减少扭摆周期测量的误差．利用动画演示，可以将初始设置情况与周期这类微小数据测量方法描述得更加细致、准确．通过Mxcel的编程功能，可以再现螺旋弹簧运动情况，由此能够让学生更好地理解实验过程各参数的测量步骤及注意事项．将具象的动画过程与单一的语言相结合，提升了物理实验课堂教学的多样性与趣味性．

此外，实验中需要捕捉大量的周期数据，按照传统方法需要花费大量精力进行数值整理与计算．利用Tracker软件辅助自动追踪挡光轴，捕获挡光轴在10个周期内的运动轨迹，可将捕捉的数据轨迹以Excel的文件形式直接导入MATLAB软件，在命令行窗口转化为矩阵的形式．通过工具包Curve Fitting中的傅里叶函数分析拟合，不仅能够直观地观察其运动轨迹，还可以得到函数表达式，从而可直接读出载物台或其他物体运动的周期值．图5中实线框处下拉，选择“Fourier”软件将自动进行数据拟合处理，虚线框中的数据即为数据处理完毕后，载物盘随螺旋弹簧运动过程中的角频率，用2π除以该数值即为扭摆法测量刚体转动惯量实验中需要的周期．

图5 Curve Fitting傅里叶函数拟合数据界面

3 数据处理

本次实验在螺旋弹簧扭转系数的确定中选用质量为0.877 kg，直径为0.089 5 m的圆柱体，所得螺旋弹簧的扭转系数K如表1所示.

表1 螺旋弹簧扭转系数K的确定

本文提及实验中弹簧的扭转系数K=0.033 1 N/m，已知支架的转动惯量为I杆支架=3.21×10-3kg·m2，I球底座=1.87×10-3kg·m2，本次实验测量的对象有：大塑料圆柱体、小塑料圆柱体、塑料球、金属圆筒和金属细杆，表2为在MATLAB软件辅助下利用扭摆法测量上述物体转动惯量的实验数据与误差.

表2 各种物体转动惯量的测定

利用Curve Fitting工具包中的傅里叶函数分析拟合直接读取周期数据与传统实验教学相比：转动周期的获得操作便捷且代入公式得到的转动惯量值相对误差较小，实验数据较可靠，具有参考价值．由实验数据可见，被测样品的实验误差均低于或在1.5%，金属物体测得的转动惯量较理论值的相对误差较大，可能由于其内部结构不均匀，可成为后续转动惯量实验改进的突破口．

4 结论

本文将MATLAB编程与Curve Fitting工具包应用于扭摆法测量刚体转动惯量的大学普通物理实验教学及其数据处理中，不仅能够科学严谨地得到规则刚体转动惯量的理论值，也能够通过傅里叶函数拟合迅速便捷地得出物体转动惯量的实验值，在掌握物体转动惯量实验原理的基础上，摒弃了传统实验数据冗长的计算步骤，同时实验数据的相对误差较小；而对于课堂教学方面，通过MATLAB编程实现图像的运动与旋转，能再现扭摆法测量的过程，便于学生的想象与理解，利用多媒体设备实现课堂教学的多元化、可视化和信息化，融教育于信息时代的社会大背景，实现教育形式的进步，贯彻教育信息化的落实．