基于改进EMD的电磁超声检测数据处理技术
2022-07-05李蓉雪杨理践高松巍刘屹然邢燕好
李蓉雪,杨理践,高松巍,刘屹然,张 佳,邢燕好,耿 浩
(1.沈阳工业大学 信息科学与工程学院,沈阳 110870;2.国家石油天然气管网集团有限公司油气调控中心,北京 100028)
电磁超声检测技术是在传统超声检测技术的基础上发展起来的一种新型超声检测技术,具有无需耦合剂、检测方式灵活、耐高温等优点,从而成为了无损检测领域的研究热点[1]。电磁超声无损检测过程中,回波信号携带了与被检工件有关的丰富信息,但受检测环境复杂,扫查振动、电子设备干扰等因素影响,回波信号往往掺杂着大量噪声,噪声的干扰使得有用信号及细节特征提取时常存在漏检和误检问题,因此需要对检测到的回波信号进行分析处理,以提高检测精度[2]。
经验模式分解(EMD)是一种自适应的信号时频处理方法,其分解得到的本征模态函数(IMF)能在不同的时间尺度上体现原始信号的局部特征,通过筛选和重构表征主要信息的IMF,以达到信号滤波的目的[3]。目前EMD广泛用于信号的降噪和识别上,ZHANG Q等[4]通过计算各阶IMF的能量大小来判别噪声信号和有用信号,根据最大能量出现的位置确定选取的重构分量,达到了超声信号消噪的目的。KONG T等[5]通过误差分析选取最佳IMF和次最佳IMF重构信号,提高了信号的信噪比,实现了对球形缺陷的识别。刘东瀛等[6]通过计算各阶IMF与原信号的相关系数筛选重构IMF分量,实现了对不同种类噪声污染的碰摩声发射信号的去噪处理。然而,这些单纯IMFs的筛选原则容易在滤除高频分量的同时丢失部分有用信息,增加后续计算的误差,从而影响检测精度。
文章以电磁超声检测信号为研究对象,提出了一种基于改进EMD的数据处理方法,利用原始信号经EMD分解后的各阶IMF与原始信号的欧式距离作为IMF筛选依据,并结合小波阈值滤波方法实现噪声去除和微小缺陷信号的有效提取。笔者对不同厚度的铝板进行测厚试验,并与真实厚度进行比较。试验结果表明,提出的算法能够在保留细节特征的前提下去除噪声,提高厚度检测的精度。
1 电磁超声检测基本原理
电磁超声检测(EMAT)主是通过电磁能、机械能、声能之间的不断转化来进行检测的。检测系统主要组成部分有永磁铁、激励线圈和被测试件等。EMAT原理如图1所示。
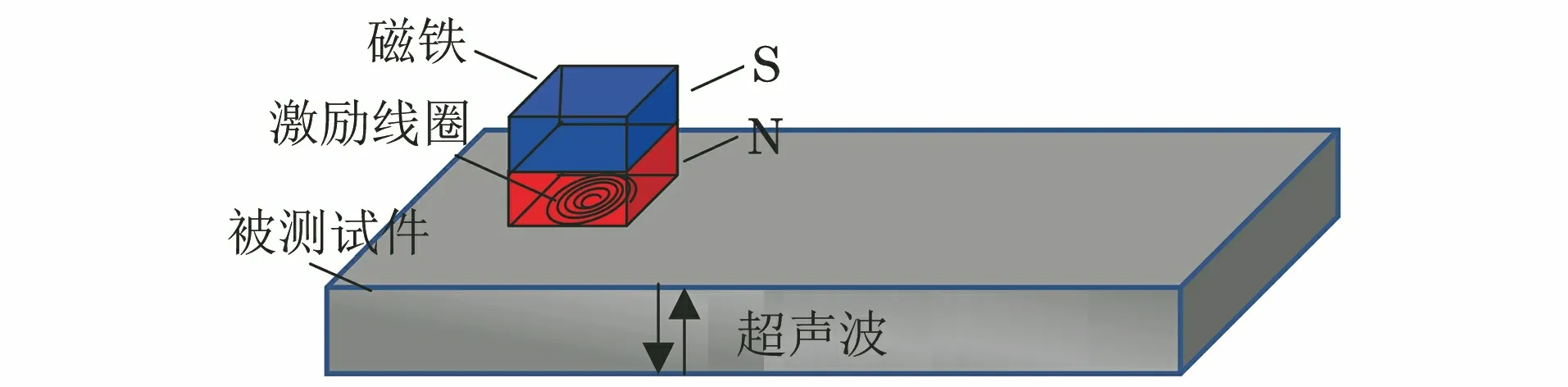
图1 EMAT原理示意
EMAT的工作过程为:将通有高频交变电流的激励线圈放置于试件表面附近。由于磁感应现象,线圈附近会产生与被测试件平行的涡流场,涡流在外界磁铁的强磁场作用下产生机械力。试件质点受力产生机械振动,同时振动的能量以波的形式沿管道厚度方向进行传播。转换关系可由麦克斯韦方程组[7]表示为
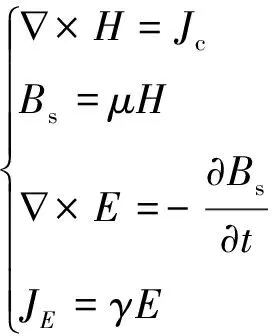
(1)
式中:∇为哈密算子;H为交变磁场强度;Bs为交变磁感应强度;Jc为激励电流密度;μ为相对磁导率;γ为电导率;E为涡流电场强度;JE为涡流电流密度。
2 超声信号处理算法
2.1 EMD基本原理
EMD能够依据信号的特点自适应地将一个复杂信号分解为一系列IMF分量,每个IMF都应满足以下条件[8]:①整个时间序列的极值的个数和穿过零点的个数必须不大于1;②任何一点的最大值包络线和最小值包络线的平均值为0。
EMD的具体分解步骤如下。
(1) 确定信号x(t)的局部极大值和极小值点,利用三次样条函数形成信号极值的上下包络线,计算其均值m(t),求出h(t)=x(t)-m(t)。
(2) 以h(t)为源信号,重复(1)步骤直到满足IMF条件,假设第k次满足条件,得到
hk(t)=h(k-1)(t)-mk(t)
(2)
式中:t为信号各时刻。
此时,第一个IMF分量c1(t)=hk(t)。
(3)用ri(t)=x(t)-c1(t)代替x(t)重复步骤(1)~(2),当rn(t)成为一个单调函数,不能再从中抽取满足IMF条件的分量时,分解结束,最终可得

(3)
式中:n为IMF序列总数。
2.2 IMF筛选原则及信号分析
EMD分解得到的IMF分量一般是按照频率从高到低排序的,对于超声检测信号来说,有用信号主要集中在低频IMF分量,其他高频IMF分量主要由噪声组成[9]。通过筛选和重构有用的IMF分量能够实现对信号的消噪和特征凸显。
由于噪声与噪声之间互无相关性,而各个特征信号之间具有较强的相关性,因此可以通过度量各IMF分量与原始信号之间的相关程度来判断各IMF中有用信号的含量。文章采用欧式距离度量各IMF(此处记为Ii)与原始信号的相似程度,其计算公式为
D(i)=dist(Ii,x(t))=
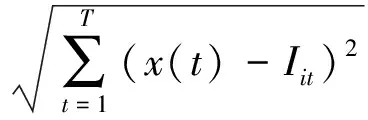
(4)
式中:D(i)为各序列欧式距离;x(t)为原始信号,Iit为各IMF序列;i为IMF分量序列数,t为时刻,T为总采样时间。
根据式(4)可知,应用欧式距离度量两个样本的相似程度时,数值越小,距离越近,相似度越大;而数值越大,距离越大,相似程度也越小。因此有用信号相似度最大的点为D(i)的最小值点。
为分析IMF分量对信号特征的表现情况,选用一段实际检测到的超声回波信号进行分析,实际检测到的超声回波信号如图2所示。对其经过EMD处理,得到8个IMF分量(记为I1~I8)及一个残余分量,EMD分解结果如图3所示。
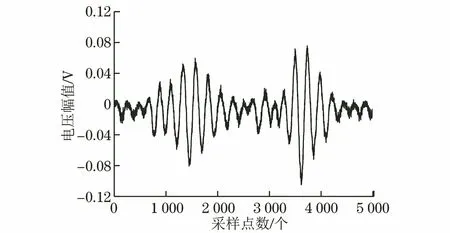
图2 实际检测到的超声回波信号

图3 EMD分解结果
从信号的各阶IMF分量可以看出,分解出的模态函数I1、I2均是噪声,I3含有微弱的有用信号。计算各IMF的能量,并采用距离度量计算其与原信号的相似度曲线,其分析结果如图4,5所示。
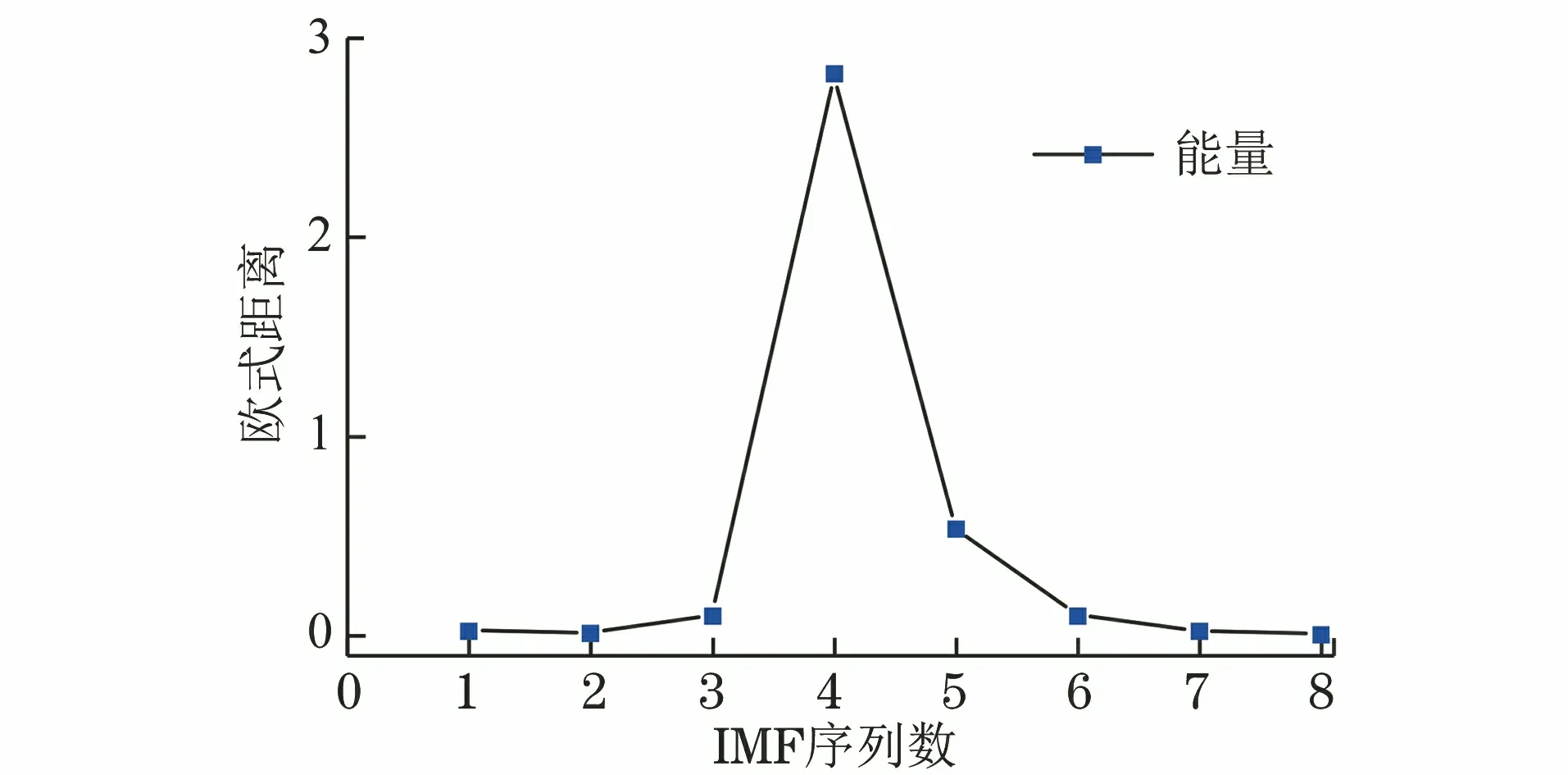
图4 IMF序列的能量曲线
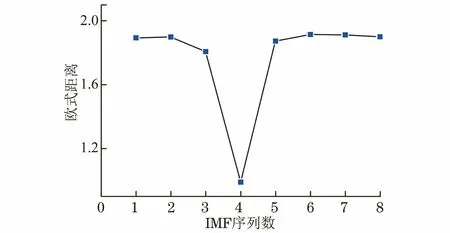
图5 IMF序列与原始信号相似度曲线
由图4,5可以看出,距离度量和能量分布中I4与原始缺陷信号的相似度最大,能量计算中I5能量值次大,距离度量中I3与原始信号的相似度次大。由于I3由大量噪声信息及微弱有用信息组成,能量幅值偏小,按照以往的能量筛选原则很容易将I3当作噪声滤除,丢失其中含有的部分有用信息。笔者分别对I3~I8及I4~I8进行重构,得到的重构信号如图6所示。
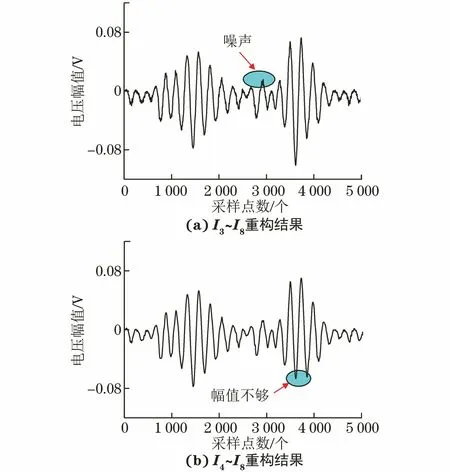
图6 部分IMF分量的重构信号
从图6(a)中可以看出,相较于图2中的原始信号,若保留I3分量将引入不必要的噪声;若在重构中剔除I3分量,将导致采样点数在3 600左右的幅值大小信息丢失[见图6(b)]。信息的丢失将导致波包峰值点位置差异,容易引起检测误差。
为解决IMFs筛选中丢失有用信息的问题,文章提出以下基于欧式距离的IMFs筛选准则,即
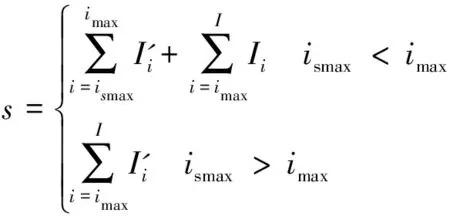
(5)
式中:s为重构后的信号,I为分解的IMF总个数,下标i为表示分量的序列号,imax为关联度最大的IMF序列号,ismax为相似度次大的IMF序列号;I'i为处理过后的IMF分量。
如果相似度次大的序列号在相似度最大的序列号前面,则说明相似度最大IMF分量前面的IMF中存在微弱的有用信号,不能直接舍去,需要再次处理后重构,如果相似度次大的序列号在相似度最大的序列号后面,则说明相似度最大的IMF前面的IMF分量均是噪声,可以直接舍去。
2.3 改进的EMD算法
根据上述的分析,含有微弱高频信号的IMF分量需要进行再次处理,文章选用小波阈值函数进行二次处理。由于含有微弱高频有用信号的IMF中噪声占主体,振荡较大,且噪声方差较小,因此选用平滑性较好的软阈值函数对其进行消噪处理。通过计算分析,最终选用紧支性较好的db8小波,分解层数为10层,并选择能够实现最优预测变量阈值的heursure阈值法则实现特征提取[10]。改进的EMD算法处理最终效果如图7所示。
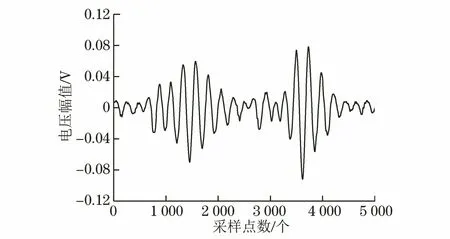
图7 改进的EMD算法处理最终效果
由图7可以看出,二次处理后的重构信号很好地保留了有用信号的幅值,且滤除了大部分的噪声,处理效果良好。
因此,改进EMD方法的具体过程如下。
(1) 将原始信号进行EMD分解,得到各阶IMF分量。
(2) 采用基于欧式距离的筛选准则对IMF分量进行择选,判断其是否需要进行再次处理,如需处理则进行小波软阈值处理,小波变换参数选择为:小波基为db8;计算120层小波分解系数的信噪比,选择信噪比最大的层数作为分解层数;阈值法则为heursure型阈值。
(3) 重构处理好的信号,得到最终的消噪信号。
3 试验与结果分析
3.1 试验平台
为定量分析所提算法的处理能力,对厚度为10 mm和厚度为15 mm的铝板进行测厚试验。试验采用收发一体检测方式,试验系统包括RITEC-5000型检测装置、双工器模块、阻抗匹配模块、用于显示和采集回波信息的示波器、由单极性磁铁及螺旋型线圈组成的换能器等,试验系统框图如图8所示。
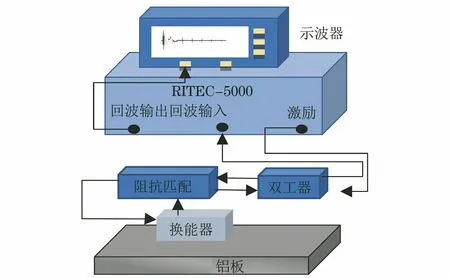
图8 试验系统框图
试验中,设置激励信号频率为2 MHz,电压幅值为300 V,螺旋线圈的有效参数为:长40 mm;宽40 mm;线宽为0.3 mm;线间距为0.1 mm。通过示波器采集回波信号数据,将采集到的数据采用文章提出的改进EMD算法进行处理,提取处理后数据的峰值点,通过遍历各峰值点,确定回波信号的峰值点信息,将相邻回波峰值点对应的时间差记为Δt,利用声程公式计算得出被测铝板厚度,即
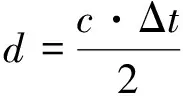
(6)
式中:d为铝板的厚度;c为被测铝板中的横波声速,该试验中取3 080 m·s-1。
为评价该算法的处理能力,将处理后计算得到的厚度值与由所采集原始信号计算出的厚度值进行比较,分别得出各自计算值与真实厚度值的相对误差
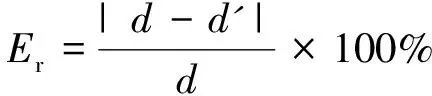
(7)
式中:Er为相对误差;d为被测铝板真实厚度;d'为根据式(6)计算的厚度。
3.2 检测数据分析
3.2.1 10 mm厚铝板的数据分析
10 mm铝板测厚原始数据及通过改进EMD算法处理后的回波信号如图9所示。
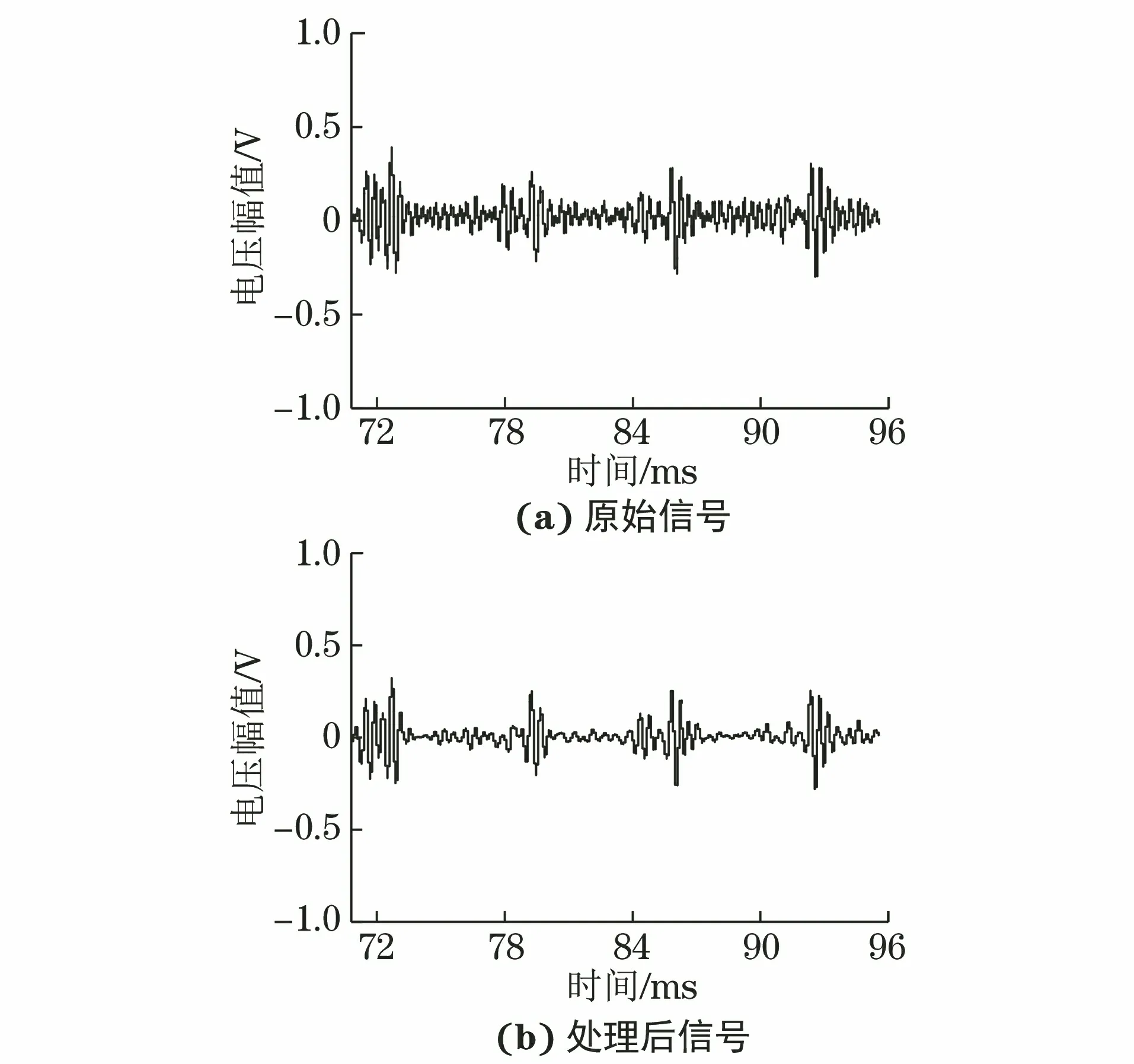
图9 10 mm厚铝板的回波信号
从图9中可以看出,经改进EMD算法处理后的数据滤除了大部分噪声并保留了幅值信息。笔者对同一块铝板进行多组试验,根据式(6),(7),由原始信号和处理后信号计算所得厚度值和误差,结果如表1所示。
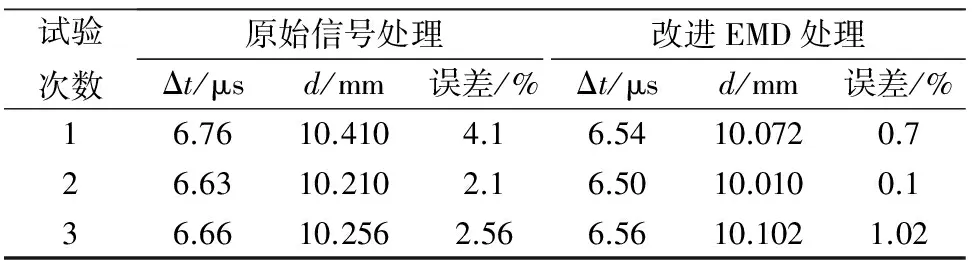
表1 不同处理方式对10 mm厚铝板的测量结果
3.2.2 15 mm厚铝板的数据分析
15 mm厚铝板原始测厚数据及通过改进EMD算法处理后的回波信号如图10所示。
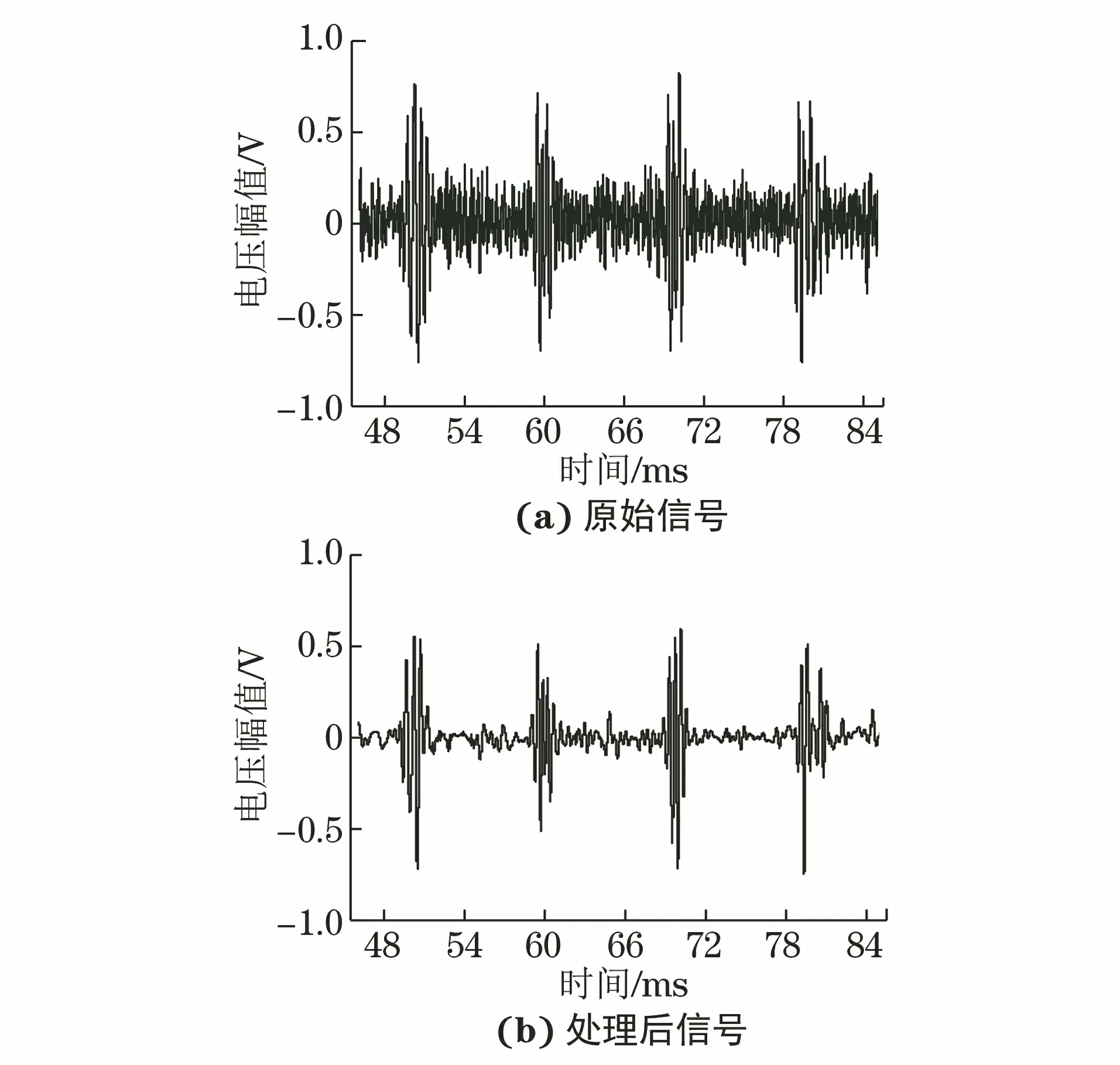
图10 15 mm厚铝板的回波信号
从图10中可以看出,提出的算法能够较好地保存回波信号的峰值点位置且滤除多余噪声。笔者对同一块铝板进行多组试验,根据式(6),(7),由原始信号和处理后信号计算所得厚度值和误差,结果如表2所示。
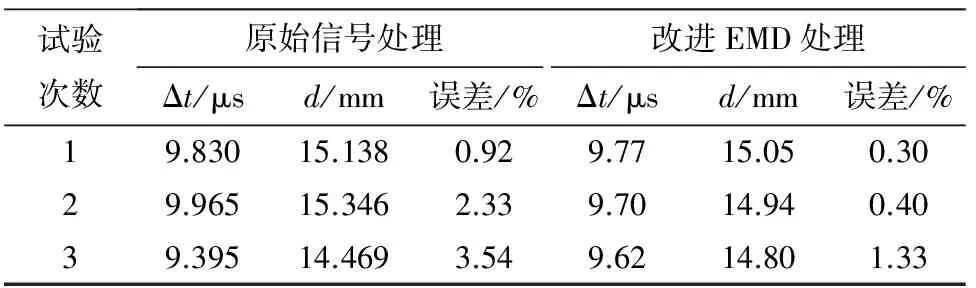
表2 不同处理方式对15 mm厚铝板的测量结果
4 结语
(1) 文章提出了一种改进EMD算法,即通过理论及信号分析提出基于欧式距离的IMFs筛选原则,并结合小波软阈值算法对数据进行滤波处理。分析结果表明,改进EMD算法处理后的信号相较于原始根据能量计算重构的信号,能够在保持较好消噪能力下实现对峰值点的准确显示。
(2) 对不同厚度的铝板进行测厚试验,结果表明,所提算法能够提高厚度检测精度,并提升信号的信噪比,对于10 mm厚的铝板,测厚最小误差为0.1%,对于15 mm厚铝板,测厚最小误差为0.3%。
