基于PM模型研究双层板中损伤引起的非经典非线性效应
2022-07-05范淼淼林懿然何爱军刘晓宙
范淼淼,林懿然,何爱军,刘晓宙
(1.南京大学 声学研究所,南京 210093;2. 南京大学 电子科学与工程学院,南京 210023)
复合材料是由两种或两种以上化学、物理性质不同的材料通过先进的制备技术组合而成的新材料,结构上由增强物和基体组成[1]。增强物起到承受载荷的主要作用,基体起到黏结、支持、保护增强物和传递应力的作用。材料会因为前期制造工艺的缺陷或者在服役过程中受到外部载荷作用而产生微裂纹。材料中的微裂纹一旦产生,如果不加以检测和控制便会在外部载荷的作用下不断蔓延生长,对整体结构安全性造成破坏[2],最终影响器件的正常运行,甚至引发重大安全事故,危害人身财产安全。
对材料中损伤的检测需求推动了无损检测技术的不断发展。超声检测具有传播距离远、穿透力强、操作方便、对材料和检测人员无害等优点,已经被广泛应用在航空航天、汽车工业、船舶制造等工业制造业领域。
根据超声波与损伤发生相互作用的不同特性,可以将超声检测分为线性和非线性两类。
Lamb波是超声波中的一种特殊形式。非线性Lamb波检测能够精准快速地检测出板状结构中微损伤的存在,并能够通过分析接收信号来识别微损伤的尺寸、位置和类型等[3-4],所以具有很高的研究价值和应用前景。
Lamb波的非线性又可以分为经典非线性和非经典非线性。早先,对非经典非线性的研究主要集中在对岩石这类非线性细观弹性材料上[5]。这类材料的非经典非线性主要表现在以下方面:①应力-应变关系表现出迟滞效应;②缓慢动力学特性,表现为当激励声停止后,弹性模量要经过很长时间才能恢复,这个过程一般需要103~104s的时间;③共振频率漂移[6],且共振频率偏移和应变成正比关系。目前用以研究非经典非线性的模型主要包括3种,即迟滞行为模型、粗糙界面模型[7]和双线性本构模型[8]。迟滞行为模型可用于描述固体中应力-应变关系的迟滞效应。粗糙界面模型认为裂纹接触面时局部接触,可用于分析有限尺寸形状体。双线性本构模型可用于解释谐波生成和混频调制等现象。
1 方法论述
1.1 Lamb波频散特性
矩阵法是求解多层板中Lamb波频散曲线的有效方法,其中又分为传递矩阵法[9]和全局矩阵法[10]。以传递矩阵法为例,其主要利用多层板中每单层的特征矩阵和每两层之间的连续性条件构成解决问题的思路。从最上面一层通过每一层的传递矩阵相乘和最下面一层建立矩阵表达式的联系,再由上下表面的自由边界条件就可以解出多层板中Lamb波的频散曲线。
以铝-铜双层复合板为例,其中铝层在上,铜层在下,每一层的厚度都为1 mm,两层之间刚性连接,计算得到双层板中Lamb波的相速度和群速度频散曲线如图1所示。
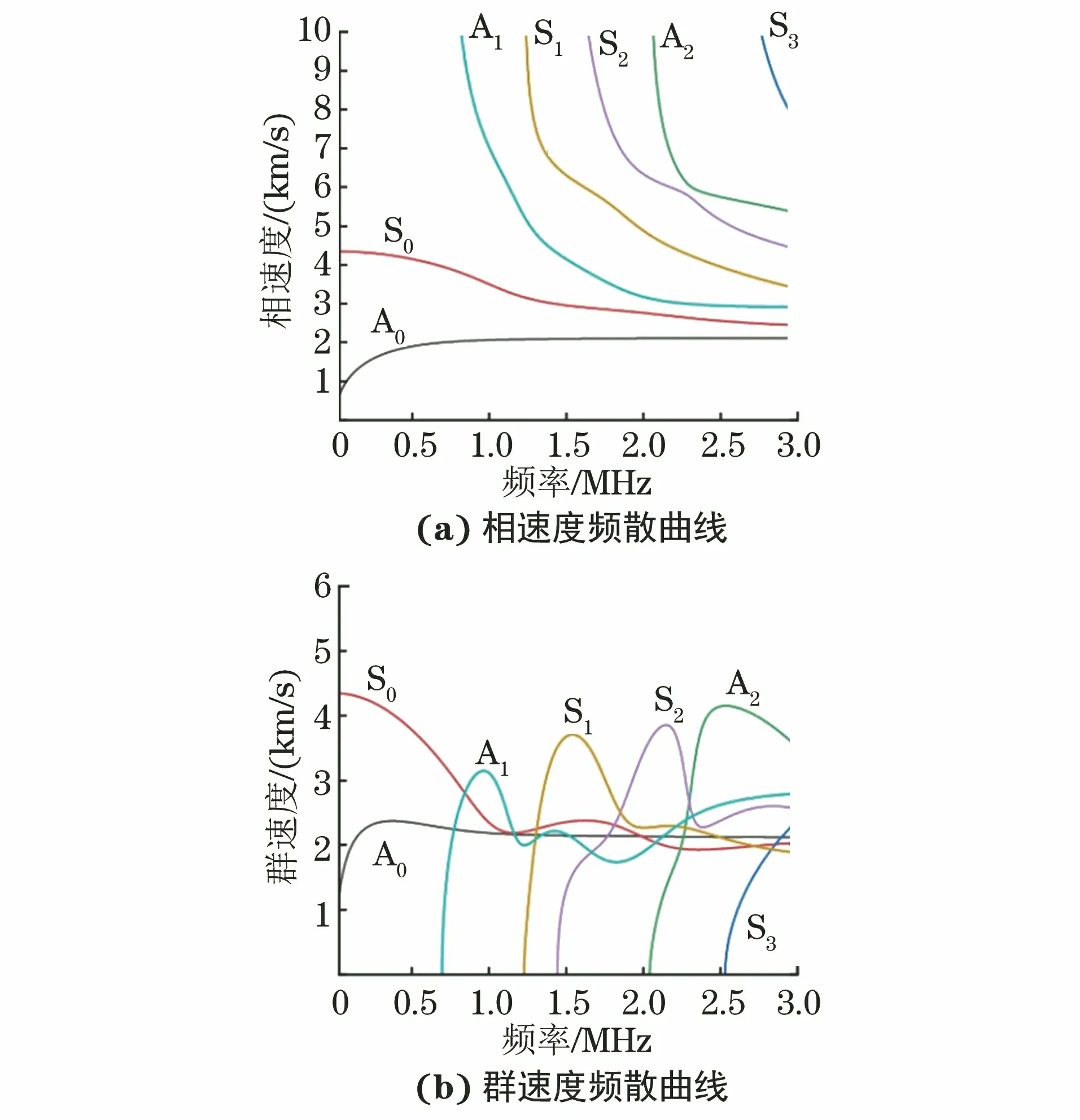
图1 2 mm厚铝-铜复合板的相速度和群速度频散曲线
1.2 PM模型基本理论
岩石、混凝土等材料的宏观弹性特性比其所组成材料的微观弹性特性要复杂得多。典型岩石的状态方程,例如应力与应变的关系表现出明显的迟滞非线性效应和离散记忆。GUYER等[5]提出将像岩石这类弹性性质由近乎刚性的颗粒和可以产生弹性变形的黏结层组成的物质称为细观非线性弹性材料(NME)。
Preisach-Mayergoyz模型(简称PM模型)是早期由Preisach等提出用以描述非线性迟滞效应的数学模型[11],之后McCall和Guyer在此基础上进行完善并通过试验验证了该模型,认为NME材料是由一种细观弹性单元 (HMEU)所构成的。这种迟滞单元有两个状态,即“打开”状态和“关闭”状态。典型的迟滞单元应力-应变关系曲线如图2所示[12]。
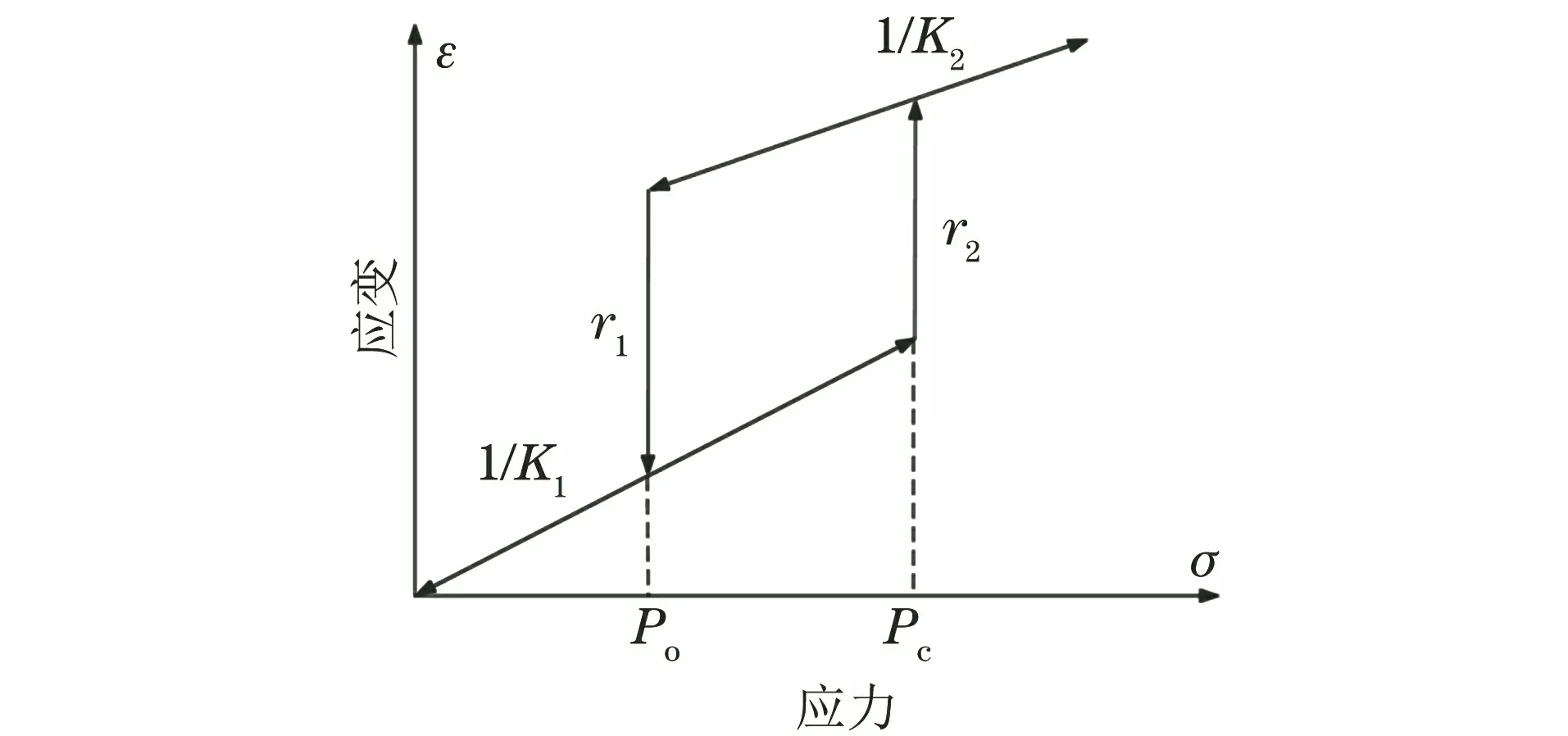
图2 典型的迟滞单元应力-应变关系曲线
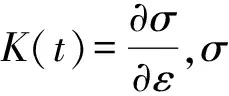
假设一拥有该应力-应变关系性质的迟滞单元最初状态为“打开”状态。孔压P从小于Pc的位置逐渐增大,应力-应变关系保持弹性模量为K1的线性关系。当P达到Pc时,应变发生突变,单元也切换为“关闭”状态,P继续增大时应力-应变关系又恢复为弹性模量为K2的线性关系。此时孔压P再减小,就需要达到Po时,应变才会发生突变,回到弹性模量为K1的线性应力-应变关系。
1.3 仿真模型
采用ABAQUS软件进行数值仿真。根据先前计算的铝-铜复合板Lamb波频散曲线的结果,采用数值仿真建立二维铝-铜复合板的二维模型,该模型尺寸为2 000 mm×2 mm(长×宽),每层厚度均为1 mm。铝层材料密度为2 700 kg/m3,杨氏模量为69 GPa,泊松比为0.33。铜层材料密度为8 900 kg/m3,杨氏模量为123 GPa,泊松比为0.35。在板的中心位置有一块损伤区域,损伤区域用PM模型表征,参数为K1=7.5×1014Pa,K2=1.0×1015Pa,r1=0.002,r2=0.001。为了简化建模,PM空间中迟滞单元均匀分布,取值为1.0×10-15。含有PM区域的铝-铜双层板二维模型如图3所示。

图3 含有PM区域的铝-铜双层板二维模型
如图3所示,以双层板的中心为坐标原点,沿板面方向为x方向,垂直板面为y方向,设置损伤尺寸为2.5 mm×1.5 mm(x方向×y方向),位置处于复合板的中心,同时包含有铝层和铜层的部分。在x=-200 mm处双层板的上下表面对称放置信号激励点。在x=xr处放置信号接收点,xr根据仿真要求选定。仿真试验考察的对象是PM模型对Lamb波作用产生的高次谐波。试验采用中心频率为100 kHz的五波峰调制正弦信号,用方程表示为
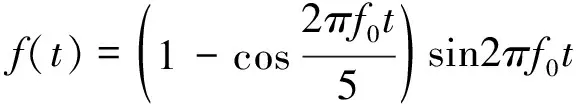
(1)
式中:f(t)为信号方程;f0为中心频率,取100 kHz;t为时间。
中心频率100 kHz五波峰调制正弦信号的时域和频域波形如图4所示。
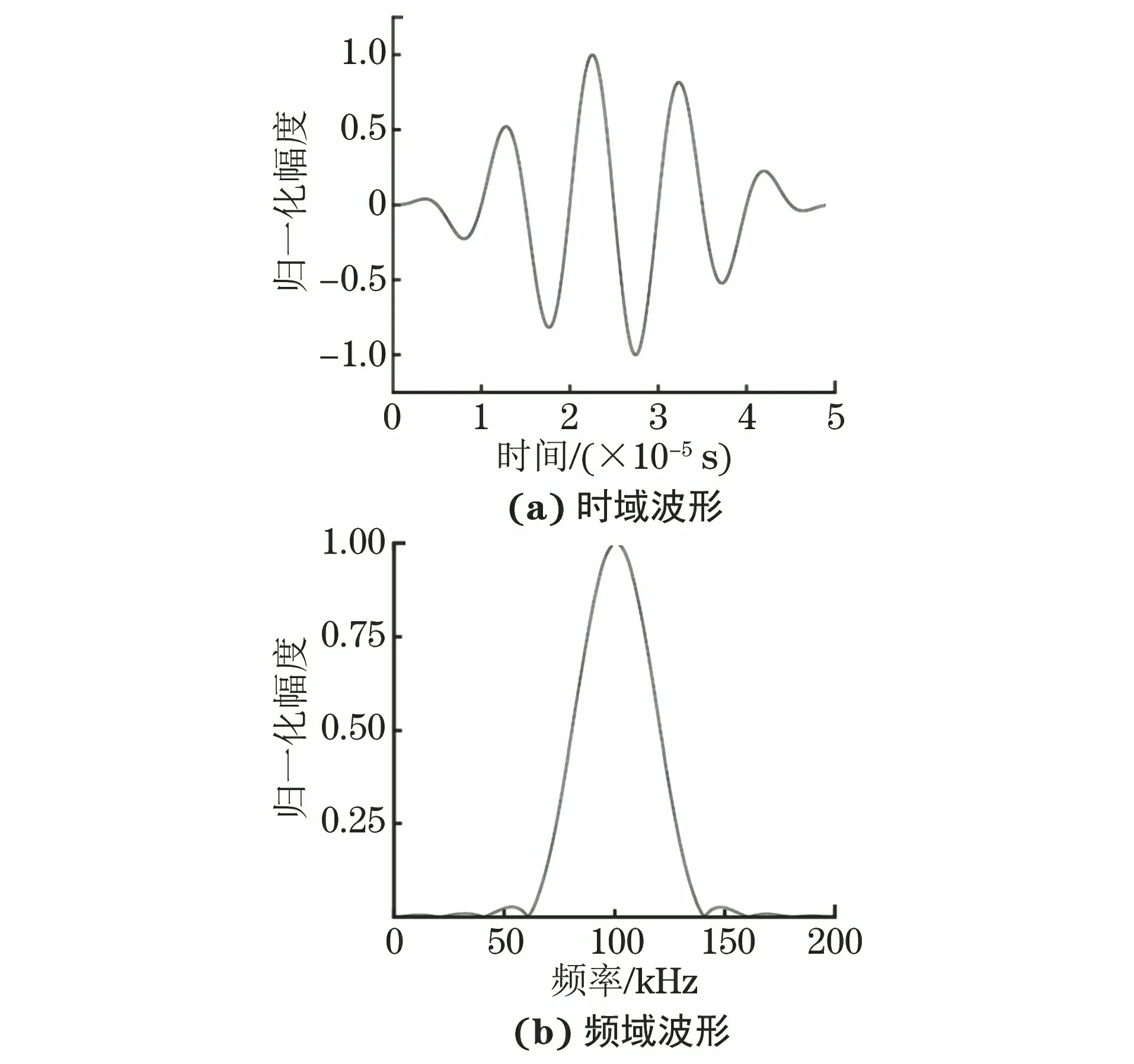
图4 中心频率100 kHz五波峰调制正弦信号的时域和频域波形
由图1可知,该声源信号的四次谐波频率为400 kHz,还未达到S1和A1模态的截止频率,在低频区域只能激发S0和A0模态,所以可以选取二次、三次、四次谐波成分作为考察对象。笔者先后使用S0和A0这两种模态来进行仿真。当上下两信号激励点发射同相信号时,可以增强S0模态的传播同时抑制A0模态。反过来当上下两信号激励点发射反相信号时,可以增强A0模态的传播同时抑制S0模态。
仿真中为兼顾结果的准确性和计算的效率,按式(2),(3)[13]设置网格的尺寸和分析步步长,即
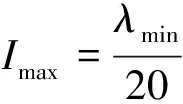
(2)
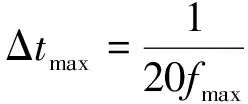
(3)
式中:Imax为网格最大尺寸;λmin为最小波长;Δtmax为最大分析步步长;fmax为最大频率。
对于100 kHz信号,A0模态波长比S0模态波长短,所以只需要考虑A0模态四次谐波的准确性,网格的尺寸和分析步步长要求分别小于0.265 0 mm和0.125 μs。故仿真中设置网格尺寸为0.25 mm,步长为0.01 μs,以满足准确性的要求。
仿真的目的主要是考察损伤与Lamb波S0模态和A0模态相互作用产生的非经典非线性。笔者同时研究了PM模型损伤的面积和PM空间中迟滞单元的密度对接收信号非线性的影响。其中PM模型由用户子程序VUMAT定义,运用二维非线性材料迭代算法[14]编写,实现每一个迭代步计算中更新应力分量。
2 仿真结果
2.1 损伤对不同模态Lamb波非线性的影响
笔者首先研究了损伤对Lamb波S0模态和A0模态传播的影响。不同激发条件下接收信号时域波形和频域波形如图5所示。
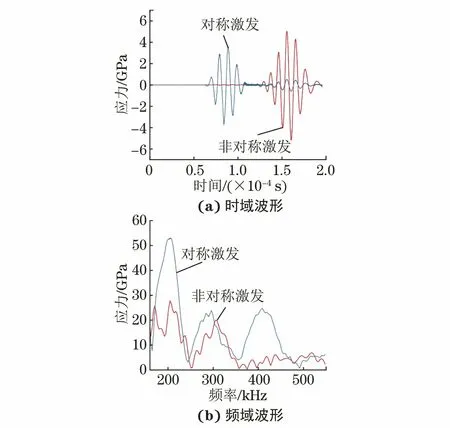
图5 不同激发条件下接收信号时域波形和频域波形
图5中两条曲线分别是在x=-200 mm上下板面两发射点激发同向同波形信号和反向同波形时在x=100 mm处接收到的信号时域波形与频域波形。从图5中可以看出,即使是对称激发或反对称激发,都会同时产生两个波包。根据两波包在时间上的距离和对称性质,可以判断其分别为铝-铜复合板中S0和A0模态。对时域波形进行分析可知,当对称激发信号时,接收信号中反对称模态A0也较为明显。相比之下,反对称激发信号时,接收信号中对称模态S0幅值较小。对频域波形进行分析可知,以S0模态为主的信号与PM模型损伤区域相互作用产生的非线性更加明显,二次、三次、四次谐波成分都可以清晰分辨。而以A0模态为主的信号与损伤相互作用虽然也产生了非线性,但除二次、三次谐波之外四次谐波成分不易分辨,并且A0模态二次谐波幅值也远比S0模态二次谐波幅值小。根据该数据,对接下来的仿真做出改进,着重利用S0模态研究PM模型产生的非线性效应。
2.2 损伤尺寸和迟滞单元密度对Lamb波非线性的影响
利用Lamb波的群速度频散特性,将信号接收点位置更改为xr=200 mm。这样可以将S0模态和A0模态的波包在时域上分离,降低A0模态对仿真的影响。同时接收点位置的设置也避免了Lamb波在模型两端反射波的影响。
为表征损伤在结构中的蔓延[15-16],采用损伤区域x方向上的尺寸和PM空间中迟滞单元密度两个参数进行研究。首先改变损伤区域x方向上的尺寸,y方向尺寸和损伤的中心位置均不变,考察引起的非线性变化。然后固定损伤区域的中心位置和面积,该区域尺寸为2.5 mm×1.5 mm(x方向×y方向)。改变PM空间中迟滞单元的密度,再次考察对非线性的影响。损伤区域x方向尺寸和迟滞单元均匀分布密度与接收信号的非线性关系如图6,7所示。
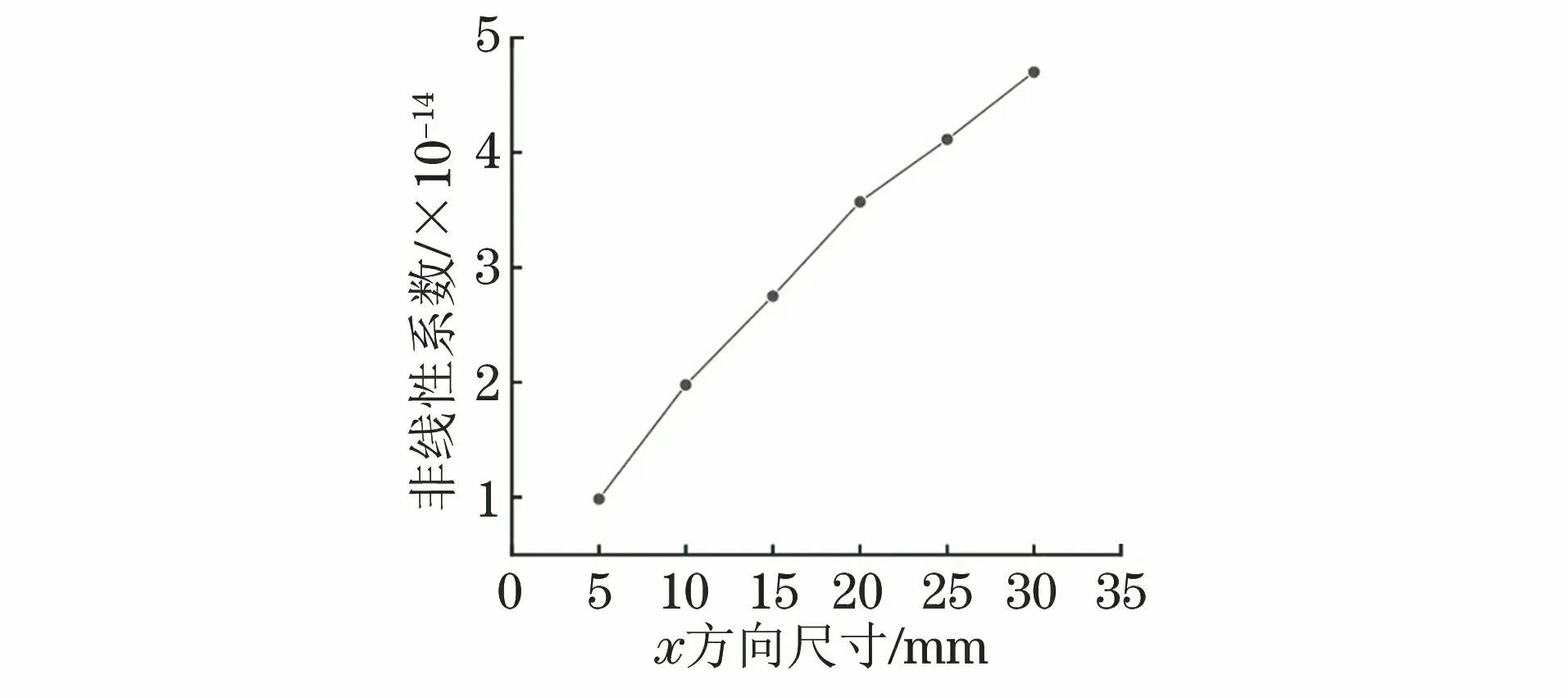
图6 损伤区域x方向尺寸与接收信号的非线性关系
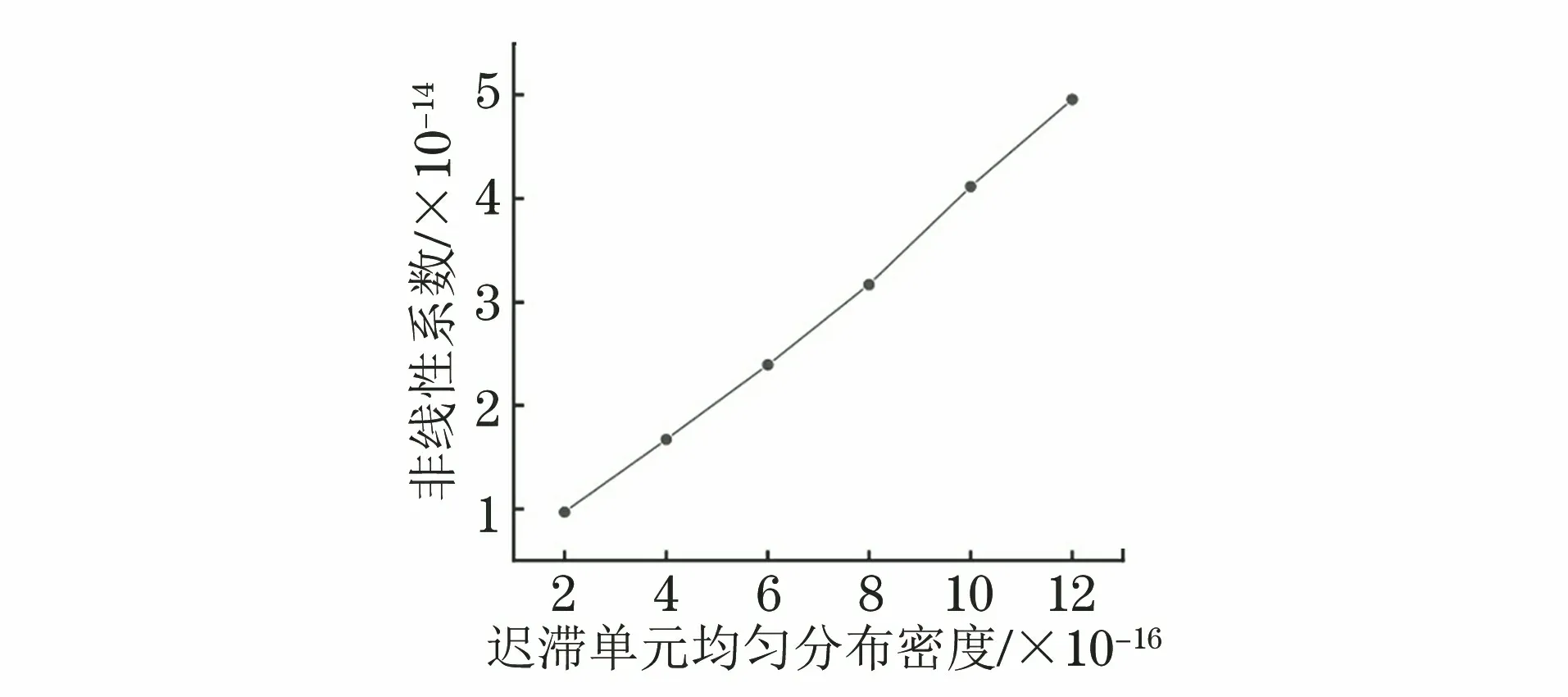
图7 迟滞单元均匀分布密度与接收信号的非线性关系
仿真利用接收信号中的二次谐波的幅值与基波的幅值平方之比来表征接收信号的非线性。由图6可见,当损伤在x方向上蔓延时,接收信号的非线性也变得更加明显,二者大致呈线性关系。由图7可见,当迟滞单元均匀分布的密度增加时,接收信号的非线性也有显著提升,二者同样呈现线性关系。损伤的尺寸和PM模型迟滞单元的密度都可以用以描述损伤的严重程度。仿真结果还表明这两个量对信号非线性的影响大致处于同一量级。因此在对材料进行超声检测时,要同时考虑损伤尺寸以及损伤局部性质的变化这两个因素,对损伤情况做完整评估。
3 结语
文章采用数值求解出双层板中Lamb波的频散曲线,对于仿真模型中损伤的描述,采用PM模型表征损伤材料的非线性特性,并采用二维非线性迭代算法实现了PM模型的定义。仿真中为避免Lamb波多模态性对结果的影响,采用了较低频率信号作为激发信号,并利用频散特性将S0和A0两个模态在时域上做分离处理。仿真结果表明双层板中S0模态Lamb波与损伤作用可产生显著非线性特征,并且接收信号的非线性可以用来描述损伤的尺寸和局部严重程度。
