基于矩阵分解的扼流适配变压器绕组漏磁检测

张朝蓓，夏鹏杰

(国网新疆电力有限公司阿勒泰供电公司，阿勒泰 836500)

扼流适配变压器绕组主要应用于电力系统中，能够对电流的干扰进行有效阻隔，保障电力运行安全[1]。扼流适配变压器绕组应当具有较好的绝缘强度、机械强度和耐热能力，但变压器在运行过程中常受到雷电过电压、操作过电压与工频过电压等影响，出现漏磁现象[2]，从而发生损坏，甚至引起电网故障以及电力系统崩溃。为此，应当对变压器绕组故障检测方法进行研究。刘星亮等[3]提出利用有限元仿真方法结合绕组分段概念，对漏磁路进行集中参数等效，并求解不同分段匝数下的漏感值。王娜等[4]提出利用ANSOFT软件模拟并分析了变压器绕组三相接地短路、匝地短路及匝间短路等状态下的漏感值，实现了对漏感特性的研究。但上述方法在分析时需要调用较多的软件及算法，计算较为复杂。

为此，笔者提出了一种基于矩阵分解的扼流适配变压器绕组漏磁检测方法。该方法采集扼流适配变压器绕组的漏磁数据，利用多层聚类算法结合最优权重译码算法进行分析，确定扼流适配变压器绕组漏磁类型；进一步采用矩阵分解方法，得到磁感应强度数据，布置磁感应强度测量点，从而实现扼流适配变压器绕组漏磁检测；最后通过仿真试验，全面验证了所提方法的有效性以及优越性。

1 漏磁检测

1.1 漏磁类型

采用纠错输出编码对漏磁类型进行分类，纠错输出编码(ECOC)是一种利用二分类问题求解多分类问题的方法。假设共有P个需要分类的种类，记为(pi,ci)，其中，pi表示全部某i个类型所对应的全部数据[5]；ci表示需要标注的类型。在使用纠错输出编码进行多分类问题求解的过程中，将二分类与多类别的个数分别设置为q与p，在编码分类矩阵M中的元素为mpq∈{1,0,-1}，其中，1与-1分别代表正类与负类，0则代表不需要进行分类[6,7]。

在分类处理过程中，多层聚类会增加不同子类别之间的混淆程度，降低分类的精度，因此针对多层次的绕组分类划分问题，采用以下步骤进行处理。

(1)

其中，ECOC编码矩阵流程图如图1所示。

图1 ECOC编码矩阵流程图

(2) 基于上述构建的编码矩阵对绕组漏磁样本数据进行训练处理，为了保证分类结果的精度，在训练处理过程中需要对分类准确率进行实时计算[9,10]。

(3) 根据上述的分类准确率计算结果，从中选出准确率最低的一组分类数据，将其划分为两个原始类别，并进一步对原始类别数据进行训练处理，形成新的编码矩阵[11]。类内聚类结果如图2所示。

图2 类内聚类结果

(4) 对新构建的编码矩阵进行重复训练，如果得到的分类结果准确率较高则重复步骤(3)；如果得到的分类结果准确率未发生改变，则完成纠错输出编码矩阵的构建。

在漏磁类型划分结果的测试阶段，将剩余的待分类样本数据输入至纠错输出编码矩阵中，对得到的输出向量结果于纠错输出编码矩阵中的每个元素进行计算处理[12]。但是在上述计算过程中因为存在不需要分类的数据，所以可能会得到错误的漏磁类型分类结果。因此，需要引入最优权重矩阵W对计算过程进行求解，得到无误差的漏磁类型划分结果。最优权重矩阵W的计算公式为

(2)

上述矩阵和编码矩阵大小相同，需要满足以下约束条件

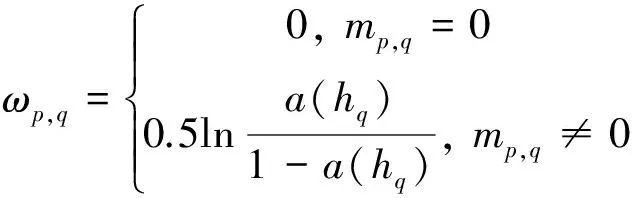
(3)

式中：ωp,q为约束条件；a(hq)为子分类器训练过程中二类分类器的分类准确率；mp,q为编码矩阵对应位置的元素，其中

∀p=1, 2, …,P

(4)

∀q=1, 2, …,Q

(5)

最优权重译码算法的类型划分译码函数[13]能够定义为以下的形式，即

(6)

式中：y∈{1, 2, …,P}，代表译码函数f(x,cp)值最小时对应行的标准值；cp为纠错输出编码矩阵第p行所对应的行向量；x为验证样本输入ECOC分类器的输出码值；d(xp,mp,q)为距离译码函数。

1.2 变压器绕组漏磁检测

从视觉角度来看，扼流适配变压器绕组漏磁检测是为了找到一块或者更多块与周围区域存在明显差异的区域。矩阵分解算法的原理就是通过信源入射到各个阵元之间的相位差，获取信源的漏磁估计信息。假设空间阵是由m个阵元组成的均匀矩阵，其中包含n个漏磁信号源，漏磁信号以平面波的形式注入到阵列上，则能够获取第k次得到的漏磁数据向量[14]，具体计算式为

X(m)=d(xp,mp,q)S(n)+N(m)

(7)

式中：X(m)为第m个阵元的输出；S(n)为n个漏磁信号组成的矢量；N(m)为m个阵元所接收到的噪声矢量。

设a(θ)为漏磁信号方向为θ的导向矢量，则能够获取以下的计算式，即

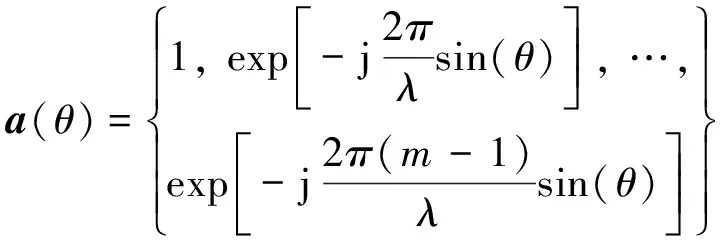
(8)

对应漏磁数据矢量的协方差矩阵能够表示为

(9)

设定RS代表任意漏磁矢量，则有

RS=a(θ)a(θ)H

(10)

a(θ)=[a(θ)1,a(θ)2, …,a(θ)n]

(11)

则前向平滑P次的漏磁数据协方差矩阵能够表示为

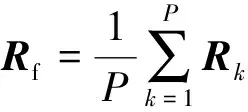
(12)

将漏磁数据协方差矩阵进行修改，则有

RSSMD=[Rf,Rs]

(13)

结合式(10)以及式(12)，能够获取以下计算式，即

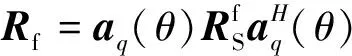
(14)

Being directed at a specific task,assuming that the initial manipulator configuration isthe initial position and attitude of the end-effector areand the desired position isJ2is the fault joint.

(15)

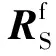
同时，q×n的Vandermonde矩阵能够表示为以下的形式，以得到漏磁后的磁感应强度数据，即

Aq(θ)=[aq(θ1), …,Aq(θn)]

(16)

aq(θ)=[1, 2, …,N(m)]

(17)

式中：Aq(θ)为磁阻率矩阵；aq(θ)为电导率矩阵。

根据获得的磁感应强度数据计算磁感应强度测量点

(18)

由于扼流适配变压器绕组的内部结构是对称的，所以在计算磁感应强度的过程中，需要考虑绕组的二维截面，并对其进行建模计算[15]。其中扼流适配变压器绕组的结构如图3所示。

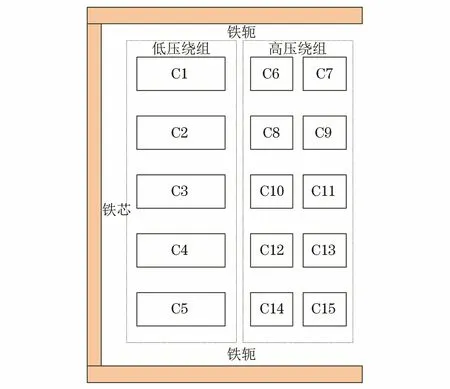
图3 扼流适配变压器绕组结构示意

综合上述分析，设定扼流适配变压器绕组的低压匝数为N1，高压匝数为N2，整个绕组区域的电流均匀分布，将铁芯部分的磁导率设定为无穷大。

在漏磁场计算模型中，需要将扼流适配变压器绕组的匝数设定为一个子绕组进行分析，同时对不同子绕组区域进行编号，即

C={c1,c2, …,cn}

(19)

综合上述分析，结合矩阵分解算法，计算扼流适配变压器绕组漏磁后的磁感应强度数据，得到磁感应强度测量点，实现扼流适配变压器绕组漏磁检测，即

(20)

式中：Az为磁矢量值；Bx为x方向磁通密度；By为y方向磁通密度。

2 仿真试验

为了验证所提基于矩阵分解的扼流适配变压器绕组漏磁检测方法的综合有效性，需要进行仿真实验。试验采用的编程软件为MATLAB 2012b。为了提高试验的可信度，将所提检测方法与文献[3]，文献[4]中的方法进行对比。

2.1 漏磁类型划分准确性

漏磁类型划分对检测扼流适配变压器绕组漏磁具有重要影响，因此以漏磁类型划分精准性为试验对比指标，进行对比试验，漏磁类型划分精度如图4所示。

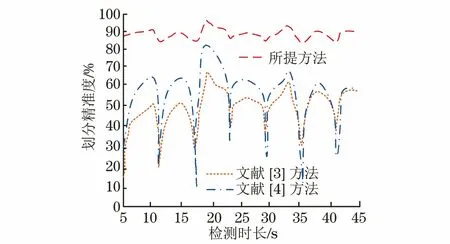
图4 漏磁类型划分精度

分析图4可知，所提方法的漏磁类型划分准确性均高于其他方法的。两种文献对比方法的漏磁类型划分准确性波动性较大，而所提方法的漏磁类型划分准确性均保持在80%以上。充分说明所提方法具有较高的漏磁类型划分精准性，能够保证漏磁检测的准确性。

2.2 漏磁点检测准确性

在完成漏磁类型划分精度验证后，需验证影响检测精度的决定性指标，即验证漏磁点检测的准确性。实际漏磁点测量结果与不同方法的漏磁点检测结果如图5所示。

图5 实际漏磁点测量结果与不同方法的漏磁点检测结果

从图5中可以看出，所提方法的漏磁点检测结果与实际漏磁结果基本一致，说明所提方法能够对变压器整体的磁感点进行均匀测量，从而得出更加合理的漏磁检测结果。两种文献对比方法的漏磁点测量结果，与实际漏磁点相差较大，不能对变压器整体漏磁进行检测，只能得到部分检测结果，其漏磁检测结果存在一定的误差。

2.3 检测延时对比

为了更进一步验证所提方法的有效性，需要对比文献[3]，[4]中方法和所提方法的检测延时，对比结果如图6所示。

图6 检测延时对比结果

分析图6可知，相比两种文献对比方法，所提方法的检测延时明显更低，验证了所提方法的优越性。

3 结语

针对传统扼流适配变压器漏磁检测方法存在的一系列问题，设计并提出了基于矩阵分解的扼流适配变压器绕组漏磁检测方法。通过精准的漏磁类型划分与漏磁点测量结果，实现了扼流适配变压器漏磁的精确检测。仿真试验结果表明，所提方法能够有效降低检测延时，提高检测精度。