数控机床刀塔锥齿轮振动噪音分析

轩 亮，万泽福，章春飞，杨 轩，洪文雄

（1. 江汉大学 智能制造学院，湖北 武汉 430056；2. 武汉大学 动力与机械学院，湖北 武汉 430072）

0 引言

国产数控机床的可靠性与世界先进水平相比还有较大差距，其中最重要的原因是功能部件不能满足其可靠性要求，特别是数控刀塔已成为制约整体机床发展的瓶颈因素。刀塔部件的可靠性会直接影响数控机床的质量与效率［1］。2020 年，陈圣文［2］探究了数控车床刀塔启动产生故障的原因，但缺乏相关实验对其故障原因进行验证。2021 年，李金凤等［3］研究表明数控机床刀塔结构缺乏可靠性会导致实际工作效率低下，其借助FMECA 方式定位刀塔产生的故障，并提出改进措施，但未考虑弧齿锥齿轮产生故障的原因。刀塔要实现刀具储备、刀具夹持切削及自动换刀等功能，在其运行过程中要求传动平稳，因此数控机床的刀塔传动常采用弧齿锥齿轮传动［4］。

弧齿锥齿轮的啮合质量直接影响系统的承载和振动等性能，由于弧齿运行过程中会产生啮合冲击，导致系统产生振动，从而使刀塔运转不稳定，产生很大噪音［5-6］。这将影响机床的动态精度和被加工零件的质量，从而降低零件的生产效率以及刀具寿命，当产生剧烈振动时，可能会导致传动系统的失效，进而降低数控机床的使用性能，弧齿锥齿轮的振动噪音问题亟待解决［7-8］。本文针对弧齿锥齿轮在结构设计中存在的问题进行改进，优化国产弧齿锥齿轮的设计参数，以期提高我国弧齿锥齿轮的啮合质量，从而提高国产机床的加工质量。

1 弧齿锥齿轮噪音产生因素

图1为我国某公司生产的一款智能数控刀塔机床所使用的刀塔，其主轴最高转速可达5 000 r/min，刀塔部分采用伺服电机分度、液压锁紧、齿盘定位的设计结构，换刀速度快、定位精度高。在该数控机床刀塔转换刀具以及加工零件的实际运行过程中，发现数控机床产生的噪音极大，观测被加工零件，发现零件的加工质量不能满足要求。在对数控机床各部件进行故障排查之后，最终判断是由于刀塔部件弧齿锥齿轮的啮合存在问题，从而引起振动。

图1 刀塔结构图Fig.1 Tool turret structure diagram

如图2 所示，样件弧齿锥齿轮为该刀塔式数控机床主轴传动部分的零部件。在弧齿锥齿轮啮合过程中，由于制造、安装误差的存在以及轮齿啮合对数、啮合点位置及瞬时传动比的不断变化，使得轮齿刚度不断变化；轮齿在实际啮合过程中会不断产生冲击，从而激发齿轮振动；同时由于支撑系统刚度不足，转子不平衡，随载荷的变动会激发齿轮整体的振动，产生噪声［9-10］。

图2 样件弧齿锥齿轮图Fig.2 Spiral bevel gear diagram of the sample

2 样件弧齿锥齿轮逆向工程分析

弧齿锥齿轮的齿面几何形状以及齿距精度对弧齿锥齿轮的啮合性能有重要影响［11］。为了分析样件弧齿锥齿轮的精度，采用激光扫描逆向工程技术对其进行研究。

2.1 点云数据的采集

点云数据采集是逆向工程的开端，点云的质量将直接影响所重构的三维模型的准确度［12］。利用扫描仪Creaform HandySCAN 700 对需要逆向的样件弧齿锥齿轮进行轮廓扫描，获得齿轮齿形点云数据。将STL 数据文件导入SolidWorks 中得到数据模型，如图3 所示。由于扫描得到的点云数据太多，笔者采用曲线扫描的方式获得3 条（齿轮大端、中端、小端）齿形轮廓曲线，通过PolyWorks Linspector Premium 软件去除其他过于离散的点云数据，导出弧齿锥齿轮大端、中端和小端的TXT 数据文件。

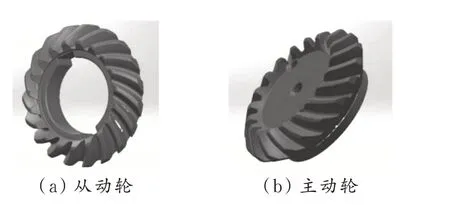
图3 样件齿轮点云数据模型图Fig.3 Point cloud data model diagram of the sample gear

将TXT 文件导入MATLAB，对得到的数据进行筛选与处理。将导出的数据去除Z轴的坐标，只保留所有点的X、Y轴坐标。由转角公式r= sqr（x2+y2）求出齿廓上点到圆心的距离，找出其中的最大半径rmax和最小半径rmin。通过坐标转化公式（1）求出扫描数据的偏转角后，采用plot 函数绘制样件弧齿锥齿轮三端数据散点图，如图4 所示。

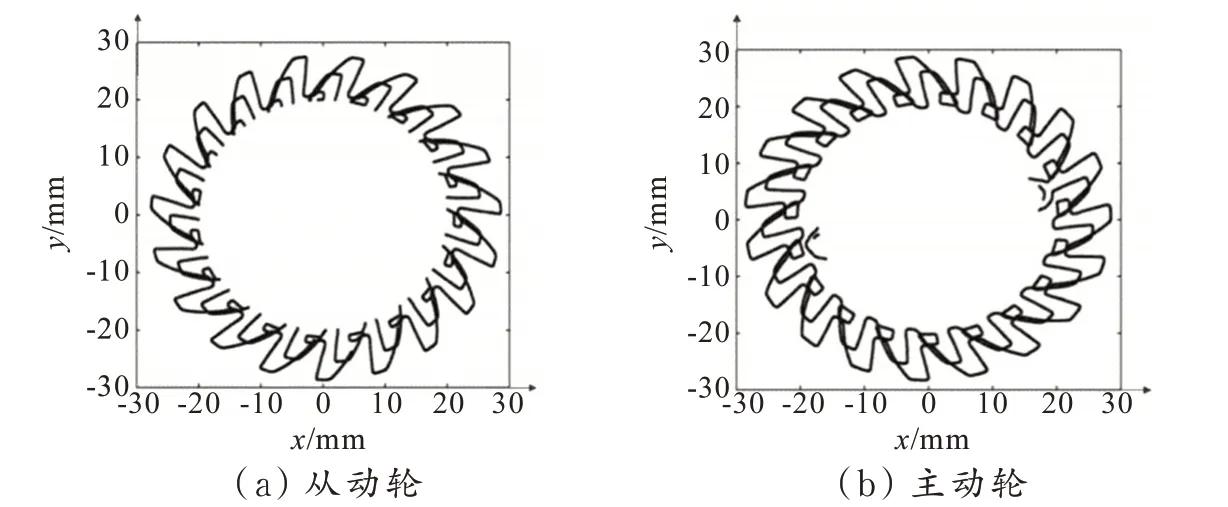
图4 样件齿轮端面齿廓图Fig.4 The tooth profile of the end face of the sample gear

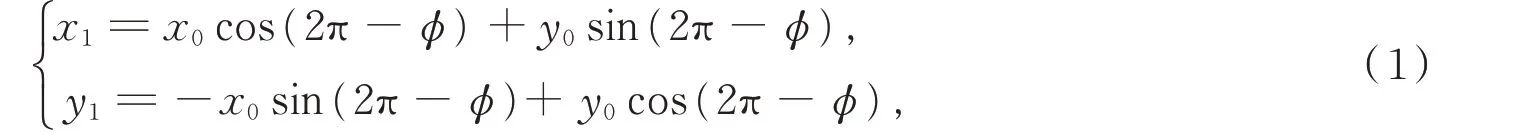
式中，(x0,y0)为选取初始点的坐标；(x1,y1)为下一个点的坐标；φ为偏转角。

2.2 样件数据处理

将扫描的样件从动轮和样件主动轮的齿廓数据和齿根圆数据以TXT 格式导出，运用MATLAB对数据进行处理，得到样件从动轮和样件主动轮齿顶圆和齿根圆上的各个坐标点，去除误差过大的数据，依次选取符合要求的齿顶圆点和齿根圆点，分别绘制其拟合圆，通过数据处理计算得到圆度误差以及各拟合圆的圆心坐标和半径。计算得样件从动轮齿廓拟合圆、样件主动轮齿廓圆的半径分别为28.388、28.095 mm。

通过样件弧齿锥齿轮齿廓拟合圆圆心的确定，将其中两个点依次与圆心相连构成两条直线，计算这两条直线之间的夹角，得到样件从动轮和样件主动轮的实际圆心点，进而计算该圆处的周节误差。由图5 可知，样件有3 ～4 个轮齿存在较大的周节误差。样件主动轮在13 号齿的周节误差最大，达到了0.318 1 mm；在4号齿的周节误差达到了0.192 5 mm；在1号齿的周节误差为-0.167 9 mm。样件从动轮在12 号齿周节误差最大达到0.203 6 mm。经计算得到样件主动轮周节误差标准值为0.129 0 mm，样件从动轮周节误差标准值为0.109 1 mm。

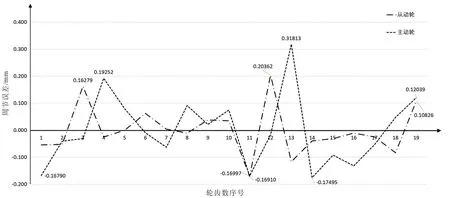
图5 样件周节误差折线图Fig.5 Folded line diagram of sample′pitch error

通过计算得到所选参考弦齿厚数据折线图（见图6）。通过齿厚分析可知，在19 个轮齿中，样件从动轮的平均所选参考弦齿厚为8.796 7 mm，4 号、12 号、14 号齿的弦齿厚偏差较大，其弦齿厚差值在0.180 0 ～0.210 0 mm，其标准差为0.121 2 mm。样件从动轮的分度圆理论齿厚值为4.710 0 mm，经测量计算得到样件从动轮的实际分度圆齿厚值为4.714 8 mm，差值为0.004 8 mm。样件主动轮的平均所选参考弦齿厚为9.242 0 mm，12 号、13 号、16 号齿的齿厚与平均齿厚值相比偏差较远，其标准差为0.068 4mm。样件主动轮的分度圆理论齿厚值为4.710 0 mm，经测量计算得到样件从动轮的实际分度圆齿厚值为4.717 8 mm，差值为0.007 8 mm。

图6 样件所选参考弦齿厚折线图Fig.6 Folded line diagram of selected reference chord tooth thickness for sample

通过分析发现，样件弧齿锥齿轮周节误差较大，使轮齿运行过程中产生冲击从而影响其运转的平稳性。轮齿的周节误差在运行过程中由于啮合磨损不断增大，这就会不断降低齿轮的实际重合度，从而进一步加剧齿面接触印痕的偏移，导致出现严重的边缘接触，使样件弧齿锥齿轮运行过程中产生振动［13］，即导致机床主轴发生振动，影响零件的加工质量。通过所选参考弦齿厚分析发现样件从动轮和样件主动轮中都有3 ～4 个轮齿的齿厚偏差过大，而齿厚偏差会影响样件弧齿锥齿轮的齿侧间隙，齿侧间隙会导致轮齿在啮合时产生齿间冲击，从而影响齿轮传动的平稳性。

由以上分析可知，齿轮的周节误差和齿形误差是样件弧齿锥齿轮产生振动的主要原因。

2.3 样件参数分析计算

2.3.1 弧齿锥齿轮主要参数计算公式［14］弦齿厚为

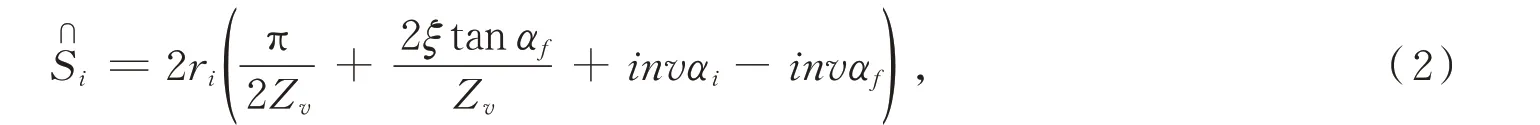
式中，ξ表示法面参数；Zv表示当量齿数；ri表示任意圆半径，mm；αi表示任意圆压力角，（°）；αf表示参考点分度圆压力角，（°）；invαi=tanαi-αi；invαf=tanαf-αf。

端面重合度为

式中，gan表示中点法向截面内啮合线长，mm；Pmm表示中点法向周节，mm；αn表示法面压力角，（°）；βm表示中点螺旋角，（°）。

轴面重合度为

式中，met表示参考点端面模数；βnm表示任意选取点处的螺旋角，（°）；Re表示外锥距，mm；Kz表示齿面扭转弧与周节的比值。

总重合度为

2.3.2 样件参数计算结果 通过对样件实物分析可知，样件齿数Z=19；通过测量得知，样件齿轮分度圆直径为57 mm；由公式d=mZ可得样件弧齿锥齿轮模数m=3。齿轮压力角选取标准值α= 20°，中点螺旋角βm= 35°。将公式（2）和生成的图4 中的各点数据导入MATLAB，通过选取任意圆半径ri、任意圆压力角αi，参考点分度圆压力角αf，经计算可得理论分度圆弧齿厚s= 4.71 mm，理论中点分度圆弦齿厚S′mn= 3.857 mm；由公式（3）、（4）、（5）及各点数据导入MATLAB 计算得总重合度ε0= 1.956 3（见表1）。通过样件参数计算分析可知，样件弧齿锥齿轮的模数过大、齿数过少、重合度低，导致该数控机床在运行过程中产生较大振动，使得数控机床在运行过程中产生过大的噪声，进而导致零件的加工质量下降，且影响机床的寿命。

表1 样件参数表Tab.1 Sample parameter list

3 样件弧齿锥齿轮改进设计

齿轮模数是齿轮的主要设计参数。从提高齿轮强度、减少激振的角度出发，一般希望齿轮模数能大一些。但是齿轮模数的增大会使得齿轮误差增大［15］。故在对样件弧齿锥齿轮进行改进时，选择合适的齿轮模数十分重要。基于此，在不改变传动比，即在保持样件弧齿锥齿轮分度圆大小不变的前提下，选择不同的模数进行重合度计算，以此来选择最优模数作为改进弧齿锥齿轮的模数。其计算结果见表2。

表2 重合度对比表Tab.2 Comparison table of coincidence degree

由表2 可知，当模数为1.75、齿数为29 时，弧齿锥齿轮的重合度最大为3.879 9，故选择模数为1.75、齿数29 作为改进弧齿锥齿轮的设计参数，以此来计算改进弧齿锥齿轮的其他参数。其参数结果见表3。

表3 改进的弧齿锥齿轮参数表Tab.3 The parameter table of improved spiral bevel gear

加工改进弧齿锥齿轮，如图7 所示，对改进弧齿锥齿轮进行精度测量，采用扫描仪对其进行扫描，得到改进弧齿锥齿轮扫描数据，将数据导入SolidWorks，生成改进弧齿锥齿轮点云数据模型图（见图8）。

图7 改进弧齿锥齿轮图Fig.7 The diagram of improved spiral bevel gears

图8 改进弧齿锥齿轮点云数据模型图Fig.8 Point cloud data model diagram of improved spiral bevel gear

由图9 可知，改进弧齿锥齿轮主动轮的周节误差最大值为0.271 1 mm，最小值为-0.162 0 mm。改进弧齿锥齿轮的从动轮10 号齿周节误差最大值为0.287 4 mm，最小值为-0.173 6 mm。经计算得到改进弧齿锥齿轮主动轮周节误差标准值为0.093 7 mm，从动轮周节误差标准值为0.099 4 mm，其周节误差标准差值与样件弧齿锥齿轮对比，改进弧齿锥齿轮的周节误差标准差值要小于样件弧齿锥齿轮。

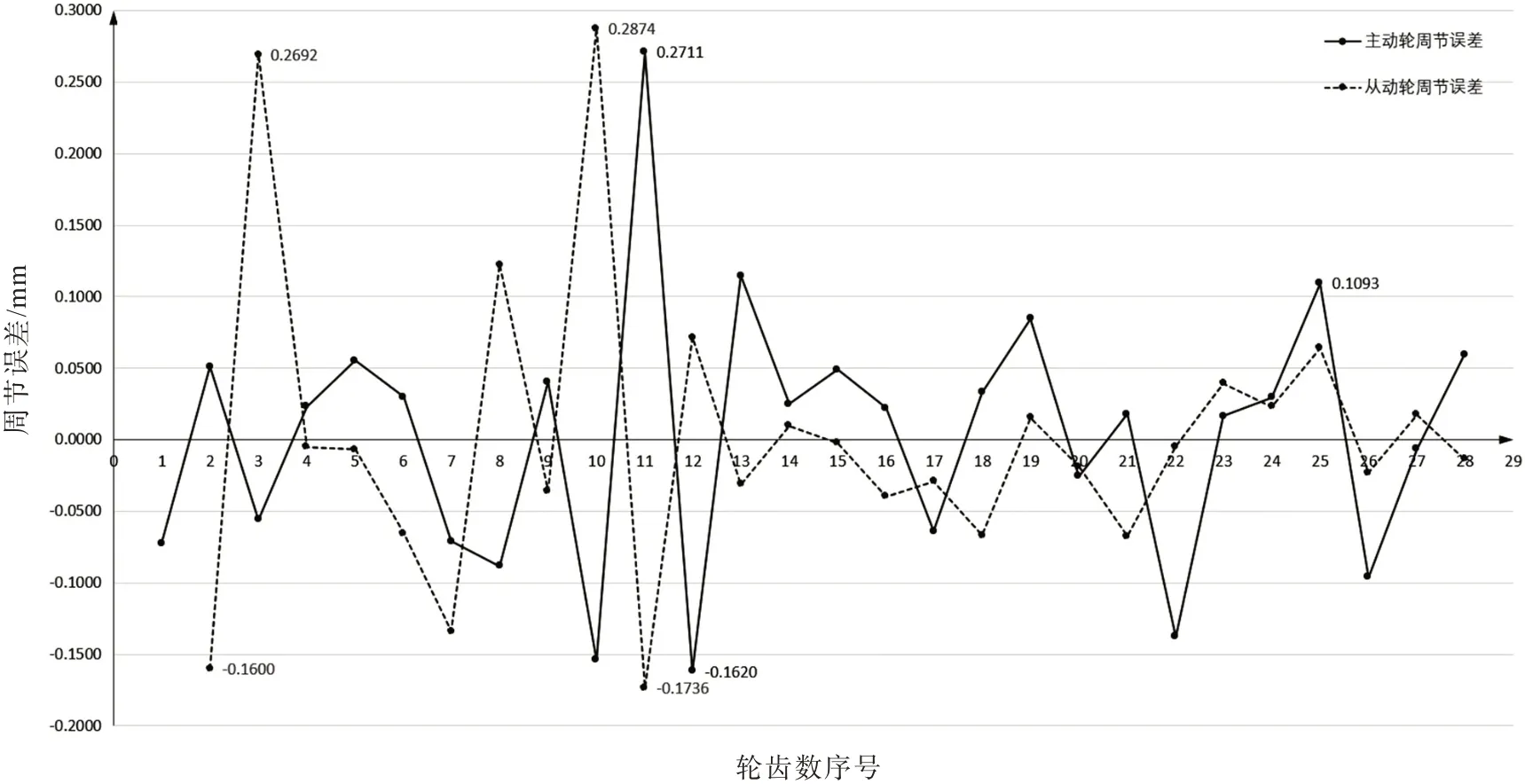
图9 改进弧齿锥齿轮周节误差折线图Fig.9 Folded line diagram of improved spiral bevel gears′pitch error

通过计算得到改进弧齿锥齿轮所选参考弦齿厚数据折线图（见图10）。通过齿厚分析可知，在29 个轮齿中，改进弧齿锥齿轮主动轮的平均所选参考弦齿厚为10.222 4 mm，5 号、7 号、14 号、15 号齿的齿厚与平均齿厚值相比偏差较远，其标准差为0.098 2 mm。改进弧齿锥齿轮从动轮的平均所选参考弦齿厚为16.247 7 mm，2 号、5 号、15 号、21 号齿的弦齿厚偏差较大，其标准差为0.065 4 mm。改进弧齿锥齿轮的理论弦齿厚为2.75 mm，经计算得到改进弧齿锥齿轮主动轮和从动轮的实际分度圆齿厚偏差值过小可忽略。与样件选取参考弦齿厚标准差相比，改进弧齿锥齿轮弦齿厚标准差小于样件弧齿锥齿轮。

图10 改进弧齿锥齿轮所选参考弦齿厚折线图Fig.10 Folded line diagram of selected reference chord tooth thickness for improved spiral bevel gears

由以上分析可知，改进弧齿锥齿轮的精度要高于样件弧齿锥齿轮。

4 实验对比分析

针对齿轮振动故障所产生的噪音分析需求，对噪音的音频图进行时频域分析。本项目采用Audacity 音频分析软件提取样件弧齿锥齿轮和改进弧齿锥齿轮的振动噪音音频文件并采用HannWindow 函数进行对比分析。HannWindow 函数是频谱分析中一个重要的部分，它修正了由于信号的非周期性并减小了频谱中由于泄露而带来的测量不准确性［16］。

图11 为GTB150-300 机床刀塔，将改进弧齿锥齿轮装入其中，在机床空载、主轴转速为1 000 r/min 的实验条件下，测得改进后的弧齿锥齿轮和样件弧齿锥齿轮在运行过程中产生的噪音音频，并进行对比分析。

图11 GTB150-300 机床刀塔Fig.11 Machine tool turret for GTB150-300

如图12 所示，通过标准自相关图可以判断噪音音频的平稳性，改进弧齿锥齿轮啮合的速度约为4 300 次/s；而样件弧齿锥齿轮啮合速度约为2 500 次/s，这与其齿轮齿数不同有关。

图12 标准自相关图Fig.12 Standard autocorrelation graph

图13 为两种齿轮振动噪音的对数逆谱图，改进弧齿锥齿轮的振动幅值较样件弧齿锥齿轮的振动幅值要小，同时改进弧齿锥齿轮比样件弧齿锥齿轮能够在更短的时间内达到稳定平衡状态。从标准自相关图和对数逆谱图可以看出样件弧齿锥齿轮振动噪音幅值要大于改进弧齿锥齿轮，其中改进弧齿锥齿轮噪音产生的周期较样件弧齿锥齿轮更加规律且频率较低，即表明改进弧齿锥齿轮在运转过程中更加平稳。

图13 对数逆谱图Fig.13 Inverse logarithmic spectrum

由图14 可知，改进弧齿锥齿轮在5 064 Hz 左右达到峰值，产生噪音分贝为-31 dB；而样件弧齿锥齿轮在1 288 Hz 达到峰值，产生噪音分贝为-26 dB，改进弧齿锥齿轮在峰值产生的噪音要比样件弧齿锥齿轮产生的低5 dB。样件弧齿锥齿轮的峰值在某个时间点突然出现且为高分贝噪音，即表明在此时样件弧齿锥齿轮在此刻会产生剧烈振动；随后噪音逐渐降低，但在2 846 和5 212 Hz 处也出现了尖峰，表明样件轮齿在啮合过程中，由于周节误差和齿形误差的存在，轮齿啮合产生齿间冲击从而导致不同时刻出现噪音波峰。样件弧齿锥齿轮的振动信号谐波峰值大多情况下都大于改进弧齿锥齿轮的振动信号谐波峰值，且改进弧齿锥齿轮的信号峰值较为平稳。显然，样件弧齿锥齿轮的振动信号的能量是大于改进弧齿锥齿轮。

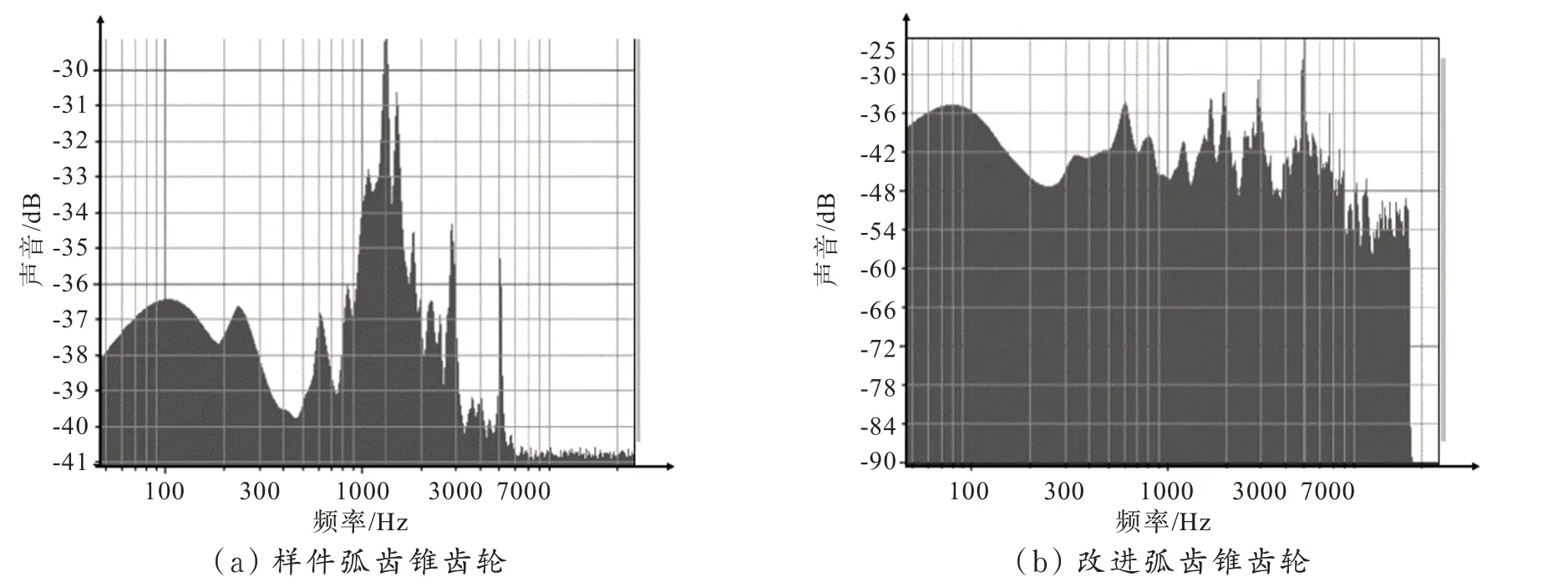
图14 齿轮频谱对比图Fig.14 Comparison of gear spectrum

由以上噪音音频图对比分析可知，样件弧齿锥齿轮的噪音频谱图分析结果与理论分析弧齿锥齿轮产生振动噪音的原因的结果相一致，即造成样件弧齿锥齿轮产生噪音的原因是由于齿距误差、齿形误差等导致的。因此，此次实验验证了理论分析结果的正确性以及改进参数的有效性。

5 结语

通过理论分析，样件弧齿锥齿轮产生振动噪音最主要的原因是由于齿轮周节误差和齿形误差所引起的，样件弧齿锥齿轮齿数较少，模数较大，导致齿轮啮合重合度降低；周节误差、齿形误差等缺陷导致齿轮不能平稳地运转，在运转过程中或加速或减速使得轮齿之间发生碰撞，从而导致齿面受到很大的动态附加载荷从而引起齿轮振动，产生噪音。通过噪音对比实验优选弧齿锥齿轮的参数，选择最佳设计参数进行改进。动态实验表明，高重合度弧齿锥齿轮有比较明显的降噪和减振效果，改进的高重合度弧齿锥齿轮的噪音平均值比样件弧齿锥齿轮的噪音平均值低1 ～2 dB。本文提出了一种基于激光扫描逆向工程对弧齿锥齿轮进行参数分析的方法，探究其产生振动噪音的原因并对样件弧齿锥齿轮进行改进，以促进国产弧齿锥齿轮提升动态性能、降低噪音、减少冲击，进而提升国产机床运行的稳定性。