自适应无色卡尔曼滤波算法的设计及其在机器人状态参数估计中的应用

徐 伟，蔡忠贸，汪塬皓，何亚妮，罗锦瑞，郭正阳，曹俊杰，刘晓东，屈斌文

（江汉大学 工程训练中心，湖北 武汉 430056）

0 引言

机器人系统要实现在复杂环境中安全、高效的运行，需要对其本身的能力状态（即机器人运动状态及能力模型参数等）有比较准确的掌控。控制方可以离线推导机器人系统的动力学模型，利用离线辨识方法来确定动力模型中的参数，便于控制器设计。但这种方法存在以下问题：①机器人系统动力学模型中不可避免地存在一些难以实现精确测量的参数，如飞行机器人的空气动力学参数，水面、水下机器人的水动力学参数等；②外界环境和机器人自身能力状态可能会随时间发生改变，即具有时变特性的模型参数，如由能量损耗引起的机器人总质量的变化、由故障引起的模型参数甚至结构的改变等；③移动机器人本身有很多状态无法直接利用传感器进行测量，如执行器部分失效引起的机器人故障参数变化。鉴于这些问题，完全靠离线的方式来确定所需要的动力学模型参数是不现实的。这时可以采取的补偿措施就是通过在线估计方法实时地、高精度地得到相应的状态参数信息［1-3］。实时预测估计方法是机器人系统处于在线模式下，根据离线参考模型和传感器信息数据，实时预测出移动机器人系统所处环境状态参数的方法。环境状态参数主要包括不可预测的风险环境、目标环境、自然环境和本身行为能力等［4-5］。

卡尔曼滤波（Kalman filter，KF）方法是在未知环境中进行状态参数估计的常用方法，但由于卡尔曼滤波方法仅适用于线性系统，限制了其在实际问题中的应用范围［6-8］。扩展卡尔曼滤波（extended Kalman filter，EKF）方法是一种非线性滤波估计方法，通过Taylor 展开式将实际问题中的非线性系统近似线性化，然后对近似线性系统实施标准的卡尔曼滤波［9］。但是，扩展卡尔曼滤波方法存在计算量大、滤波不稳定的问题，虽然对滤波方法提出了各种分解、补偿算法以改善计算的稳定性和提高计算效率［10-11］，但卡尔曼滤波方法所固有的缺陷仍然无法解决。无色卡尔曼滤波（unscented Kalman filter，UKF）方法通过一定数量的采样点，对状态的概率密度函数做近似［12］，具有比扩展卡尔曼滤波方法更好的估计精度和鲁棒性，以及相当的计算量，但由于无色卡尔曼滤波算法仍然是以系统准确的先验信息为基础，因此本文提出一种基于MIT 规则的自适应无色卡尔曼滤波（MIT adaptive unscented kalman filter，MIT-AUKF）算法，该方法基于自适应控制中利用梯度下降法调整或更新未知参数的方法，设计以信息方差的实际值与估计值的差作为无色卡尔曼滤波器的自适应指标参数，在线对滤波器中的噪声方差参数进行调节。

1 无色卡尔曼滤波算法原理

无色卡尔曼滤波算法的原理是基于“高斯分布比其他非线性函数更易于逼近”这一理论。无色变换是无色卡尔曼滤波的核心基础，即通过相当数目的采样点来近似输入变量的概率分布，将其输入到非线性函数中，获得相应的非线性输出，然后再根据新的输出点来获得输出量概率分布的近似值［13］。

无色卡尔曼滤波仍然以线性卡尔曼滤波为基础，只是在求状态参数经非线性方程传播后的均值时，对非线性方程进行了无色变换［14］。其具体算法如下：

1）初始化

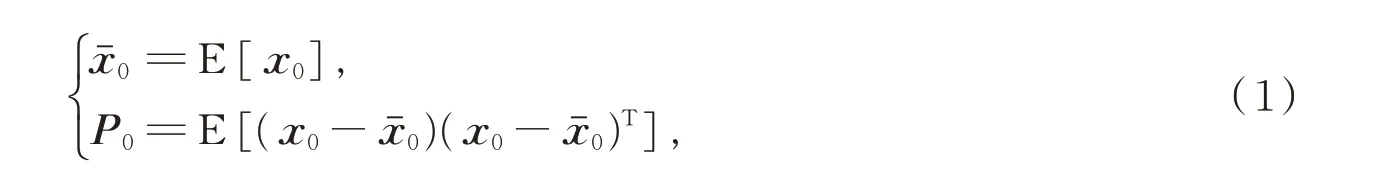
式中，表示初始状态向量的期望均值；P0表示初始状态量的协方差期望值。

2）计算sigma 点，根据随机向量x的均值和方差Px构造一组位于均值附近且关于其对称的离散sigma 点，记为χi（i=1，2，…，2n）：

式中，（*）i代表矩阵*的第i列；λ=n（α2-1），α为控制sigma 点分布的常数。

3）时间更新

式中，Qω表示已知系统的过程噪声；和表示权系数；h(*)表示相应维数的系统方程；uk表示相对应的可控制输入量。

4）测量更新

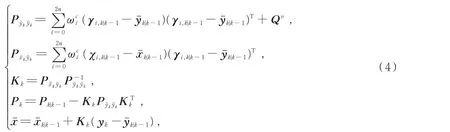
式中，Qυ表示测量噪声方差矩阵的估计值，且

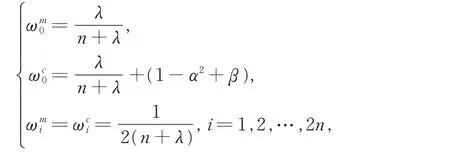
式中，β表示非负常数，其作用是使变换后的方差含有部分的高阶信息。

2 基于MIT 规则的自适应无色卡尔曼滤波算法的设计

与其他非线性估计方法相比，无色卡尔曼滤波算法在状态参数估计的准确性、算法的实时性等方面有较大优势，但是由于无色卡尔曼滤波本质上还是一种卡尔曼类滤波算法，所以无色卡尔曼滤波良好的滤波性必须以系统准确的先验信息为基础［15］。但是系统本身器件的不稳定性和外部环境的不确定性给实际环境中过程噪声、测量噪声统计特性的准确描述带来较大影响。如果先验噪声统计特性与系统的实际噪声统计特性不相符时，无色卡尔曼滤波性能可能会严重下降，甚至导致滤波呈现发散。

为了克服无色卡尔曼滤波上述缺点，设计具有噪声统计特性自适应能力的滤波器是行之有效的方法，即当系统的实际噪声统计特性未知或发生变化时，自适应滤波器能够自动地调节自身参数，以满足实验的需求，减少先验噪声信息对于滤波器性能的影响，有效地提高滤波器的稳定性和估计的准确性。

本文是基于由麻省理工学院提出的MIT 规则，即自适应控制中利用梯度下降法调整或更新未知参数的方法［16］。该方法以信息方差的实际值与估计值的差作为自适应无色卡尔曼滤波器的指标参数，在线对无色卡尔曼滤波器中的噪声方差参数进行调节。

在（1）式～（4）式中有6 个需要设计的参数，即：无色变换设计参数α和β、过程噪声矩阵Qω、测量噪声矩阵Qυ、初值方差xˉ0、初始矩阵P0。其中，①初值方差和初始矩阵对滤波器估计方法的影响不大，随着滤波过程的进行可以忽略不计；②无色变换设计参数α和β仅会对非线性系统的高阶近似项产生影响，不能改进算法的性能；③作为系统的先验信息，过程噪声矩阵和测量噪声矩阵会影响算法估计的精度和鲁棒性，如果两者的分布特性大于实际噪声，在统计结果中可能会使滤波发散；如果分布特性小于实际噪声，就会造成真值的不确定范围过小，产生偏估计。所以，过程噪声矩阵和测量噪声矩阵是在线进行自适应调节的主要参数。

从算法设计角度来看，自适应滤波器的设计应该能够同时对过程噪声和测量噪声进行调节，但是实际环境中很难确定是哪一种噪声引起的误差，如果同时对这两者进行更新，算法很难保证稳定性。因此，本文进行实验验证时，只讨论过程噪声发生突变时系统的自适应滤波器的性能。

2.1 自适应机制和指标参数

由于过程噪声和测量噪声的影响，如果以最小化测量值与估计值的差为目标值，这种算法本身的收敛性有待理论上的证明，而且还存在数值不稳定的问题，导致滤波器性能的下降［17］。所以，本文算法以新息方差的估计值与真实值的差作为设计滤波器的目标值。

新息方差的真实值可以用以批量为N的实际新息方差的均值Sk来近似计算：

式中，yk为时刻k的测量值；为相应的无色卡尔曼滤波器估计值，两者的差vk是新息值。

由无色卡尔曼滤波算法的测量更新（4）式，可得新息方差的无色卡尔曼滤波估计值

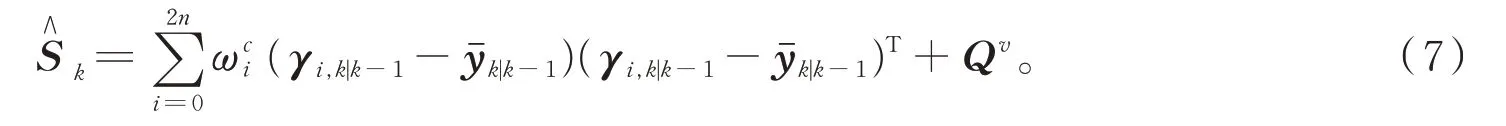
选取自适应的指标函数为

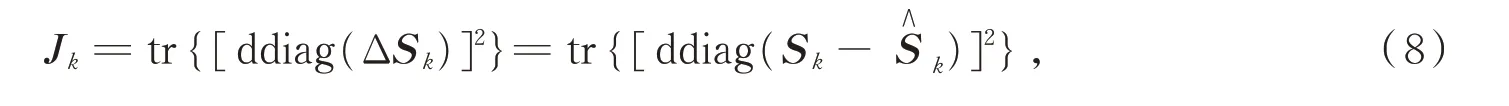
式中，ddiag（*）是以ΔSk为对角线元素的对角矩阵，tr（*）是矩阵的迹。与新息本身相比，ΔSk对系统统计特性的变化更加敏感。

基于MIT 参数更新过程，将相对于参数的负梯度方向作为指标函数参数的更新方向，即

式中，为k时刻噪声协方差矩阵第m行的对角线元素；ηk是自适应调节率，用来控制收敛速度。

2.2 自适应的无色卡尔曼滤波算法

按照MIT 规则，自适应参数的迭代机制可表示为

式中，

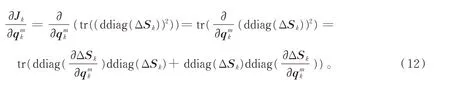
由（8）式得

根据（5）式和（6）式可得

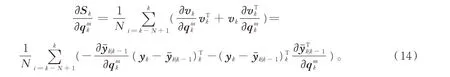
由（7）式计算滤波估计值的导数得

1）初始化

2）时间更新：将上文中标准的无色卡尔曼滤波算法（2）式和（3）式逐项对求导，可得

3）测量更新，对标准的无色卡尔曼滤波测量更新方程（4）逐项对求导，可得

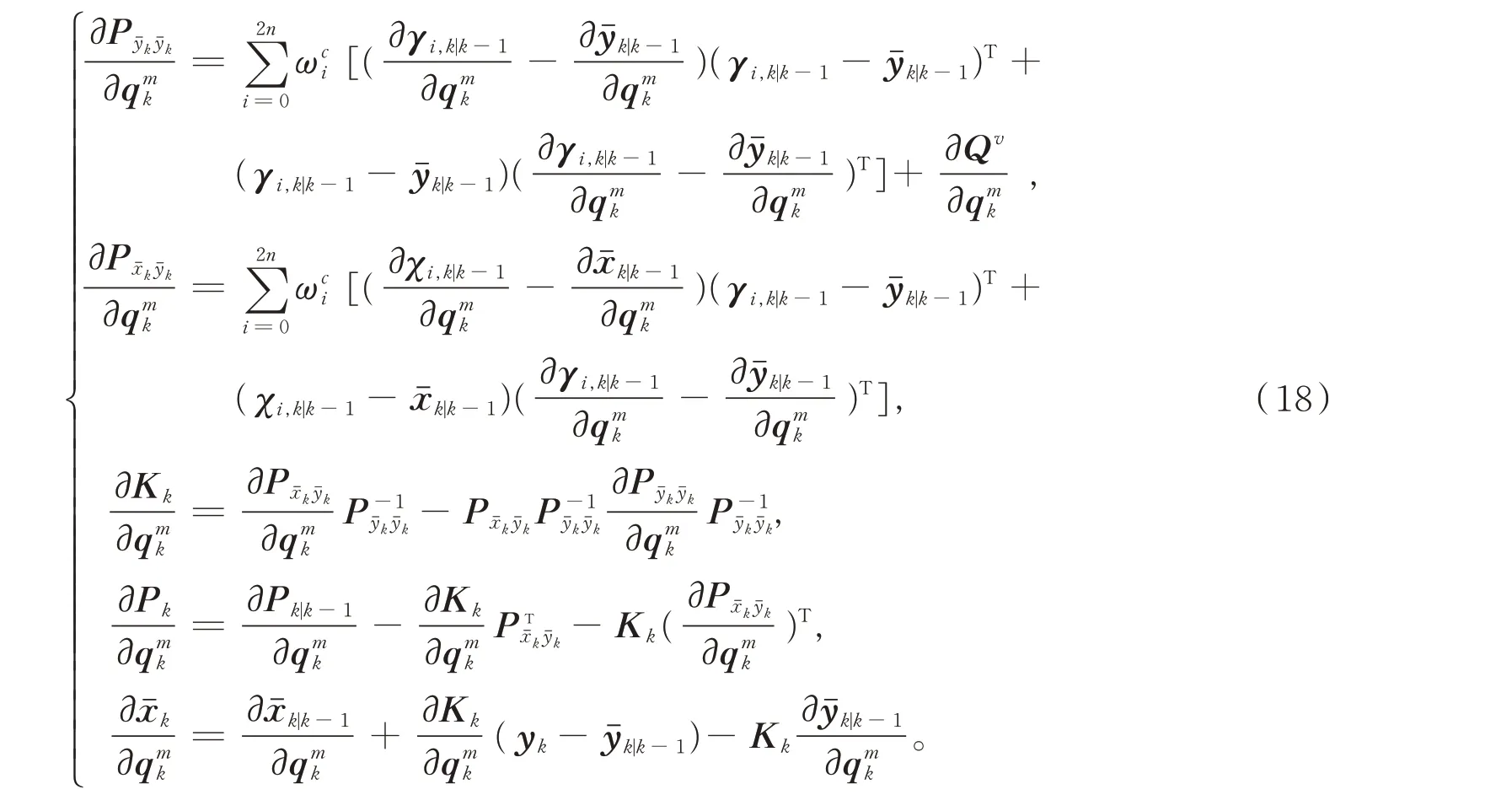
2.3 算法的渐近稳定性分析

如（9）式所示，ηk很小，（11）式中最后更新项的值也很小，那么变化比较慢，k时刻之前的估计值对梯度下降的影响很小，可以近似认为是一个常量qm0，参数的迭代更新方程就会趋近于

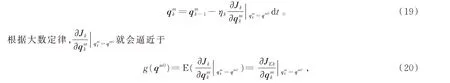
式中

则（19）式变化为

这样，qk就会渐近于下面的常微分方程解的曲线：

式中，g（q）如（20）式所示，可以得出当时间k趋向于无穷大时，qk会以概率1 收敛于JE（q）的局部极小点；由于无色卡尔曼滤波是一个稳定的稳态滤波过程，（17）式和（18）式在无色卡尔曼滤波基础上对进行求导运算，那么（17）式和（18）式所示的系统也应该是稳定的，进而系统的估计状态应该是一致有界的，即本文设计的自适应无色卡尔曼滤波是稳定的。

2.4 实验验证

通过如图1 的正交全方位轮式移动机器人来验证自适应的无色卡尔曼滤波算法的应用。

图1 正交全方位轮式机器人Fig.1 Orthogonal omni-directional wheeled robots

移动机器人的动力学模型如下：

式中，所有参数的含义及初值见表1 所示。

表1 参数含义及初值Tab.1 The meaning and initial values of parameters

定义系统状态向量和测量向量为

设采样周期为Ts= 0.01 s，系统测量值受到协方差矩阵为Rv= diag（10-8，10-8，10-8）的白噪声干扰。选择无色卡尔曼滤波的参数如下：

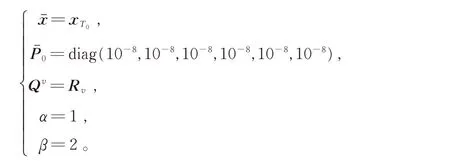
同时，为了验证自适应无色卡尔曼滤波算法的估计性能，假设系统的过程噪声在t= 10 s 时发生突变，使系统在10 s 后先验过程噪声与实际情况不相符，以此检验算法的稳定性。

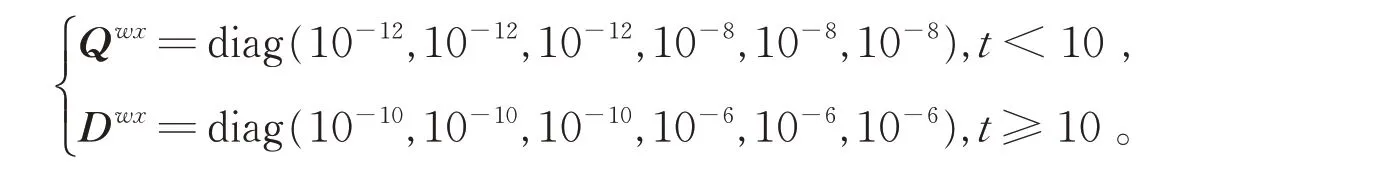
算法的其他参数设置如下：

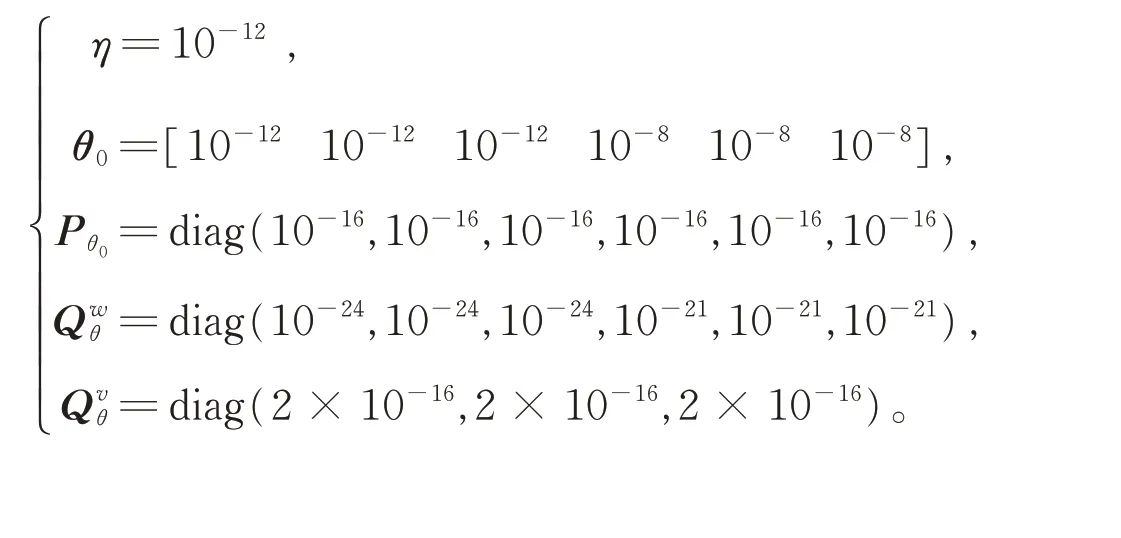
从常规无色卡尔曼滤波（UKF）算法和基于MIT 规则的自适应无色卡尔曼滤波（MITAUKF）算法的运动仿真结果图2 和图3 可以明显看出：当噪声强度发生变化时，由于先验信息不能够准确反映这种变化，普通无色卡尔曼滤波算法的估计具有较大的误差；而基于MIT 规则的自适应无色卡尔曼滤波算法则能通过自适应性能在线地估计过程噪声方差，在噪声变化的时刻仍然能保持良好的估计结果。同时，由图3 可以看出，当系统实际的过程噪声发生突变时，虽然基于MIT 规则的自适应无色卡尔曼滤波算法给出了较好的估计结果，但其状态估计误差与发生变化前后相比还是有所增大，因为系统本身的原始噪声越大，估计算法的准确程度就越小，所以该结果仍然符合客观物理规律。

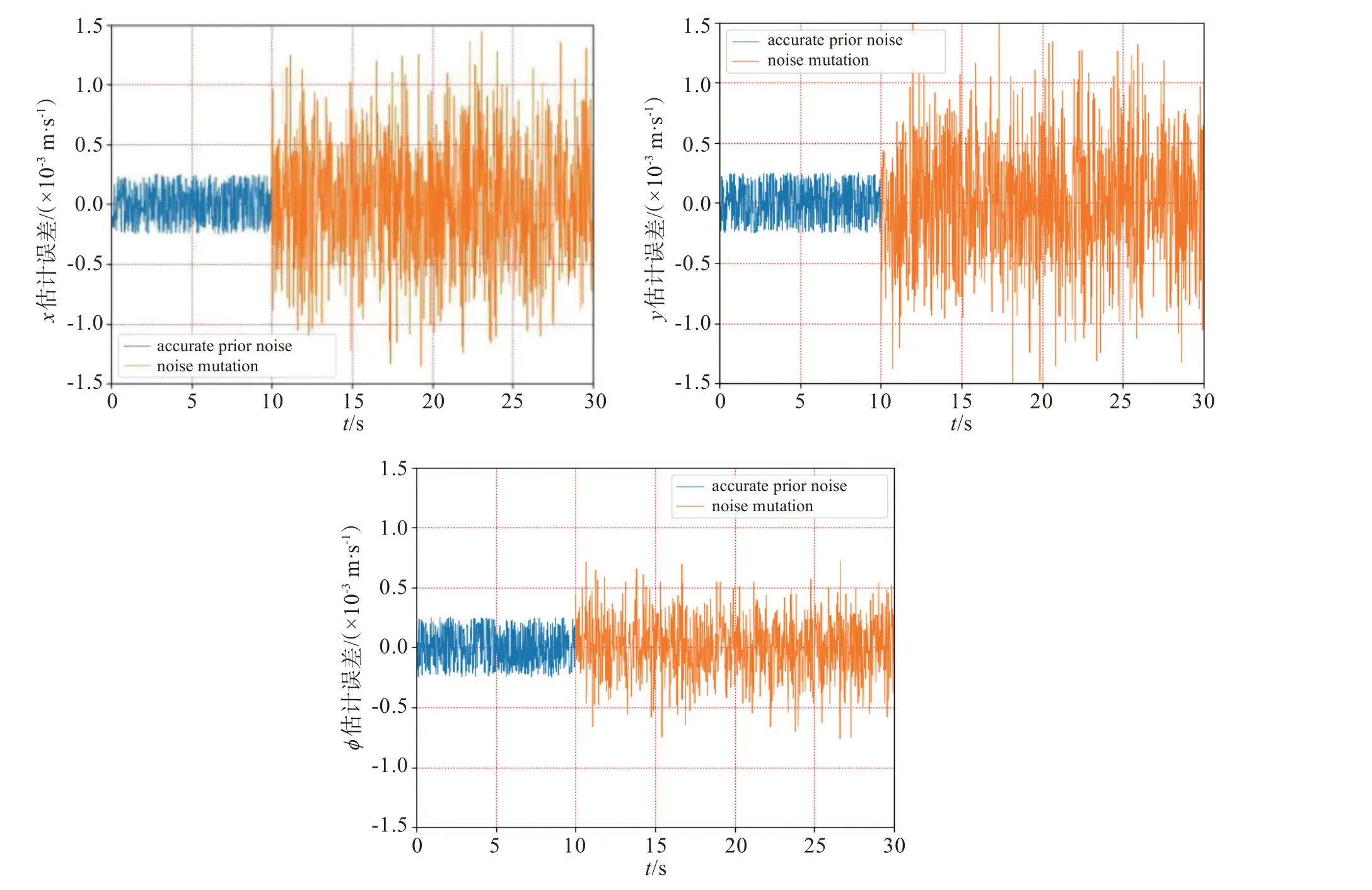
图2 普通UKF 运行结果Fig.2 Simulations of UKF

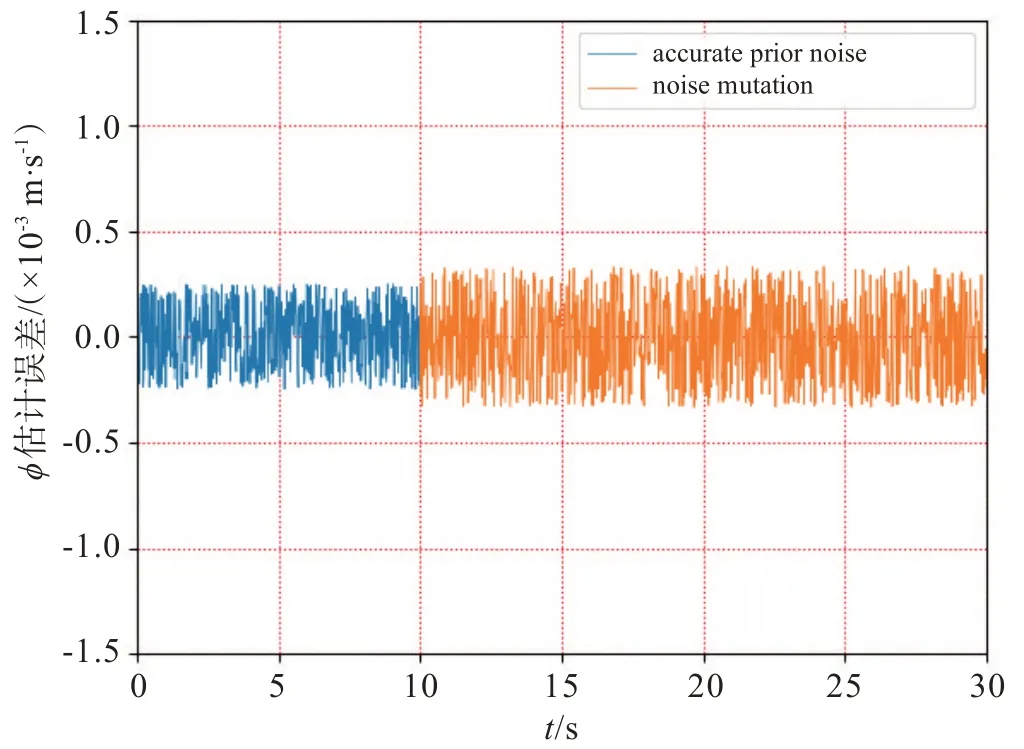
图3 MIT-AUKF 运行结果Fig.3 Simulations of MIT-AUKF

3 结语

卡尔曼滤波和无色卡尔曼滤波算法在状态参数估计中应用虽然十分广泛，但其算法自身存在的局限可能会严重影响其性能。本文在基于MIT 规则的基础上设计了一种带有自适应机制的无色卡尔曼滤波算法，以过程噪声矩阵为主要调节参数。以信息方差的实际值与估计值的差作为指标参数，利用梯度下降法更新未知参数实现自适应控制。从理论分析和实验结果可以看出，具有自适应机制的无色卡尔曼滤波对于噪声突变能保持良好的估计结果。如该算法的自适应机制（11）式所示，每个自适应参数只对应一个可调节参数，调节起来相对比较简单，使程序迭代设计更加方便简洁。该算法对于机器人系统中无法精确测量的环境状态参数、具有时变性的机器人特性参数等的估计具有良好的鲁棒性，在工程实践环境中具有良好的应用前景。