一类非线性微分方程的整函数解

刘欣杨，徐泽坤，吕巍然

(中国石油大学 理学院，山东 青岛 255680)

1 问题的提出

本文中的亚纯函数通常表示为复平面上的亚纯函数。我们将采用Nevanlinna理论,通常用T(r,f)表示f的特征函数,m(r,f)表示均值函数,N(r,f)表示极点计数函数;与往常一样,S(r,f)表示满足S(r,f)=o(T(r,f))的量，其中r→∞,允许除去一有限对数测度的集合(参见文献[1-2])。

复微分方程是复分析中一个重要的研究方向，方程解的存在性、唯一性和增长性是其非常重要的研究内容。借助Nevanlinna值分布理论对复微分方程的研究已得到了丰硕的成果，相关内容可以参见文献[3-6]。

2004年，Yang等[7]证明了下面的结果:

定理A[7]方程

4f(z)3+3f″(z)=-sin(3z)

最近，Gundersen等[8]推广了定理A，得到下面的定理:

定理B[8]设p(z)和q(z)为非零多项式,α(z)为非常数整函数。若方程

p(z)f(z)3+q(z)f″(z)=-sinα(z)

有整函数解,则α(z)=3az+b，其中:a,b为常数,p和q为常数,且满足27p=4q3a6，f(z)=c1eiaz+c2e-iaz，其中常数c1和c2满足c13=-e2bic23，2ipc13=-ebi，3pc1c2=qa2。

本文，我们进一步推广定理B，得到了如下结果。

定理1设p,q,r和s为非零多项式,α为非常数整函数。如果p或者r为常数,且

pf3+qf″=reα+se-α

(1)

有超越整函数解,则α=3az+b,p,q,r和s退化为常数,且满足27prs+a6q3=0,

f(z)=c1eaz+c2e-az,

这里c1和c2为常数,满足p2(c1c2)3=rs,3pc1c2+qa2=0。

为了进一步研究,我们提出以下问题:

问题1如果在定理1中去掉限制条件“p或者r为常数”,结论如何？

2 定理1的证明

定理的证明主要用到下面的结果。

引理1[1,9](Clunie引理)设P1(z,f),P2(z,f)是关于f的微分多项式,其系数aλ满足T(r,aλ)=S(r,f)。若f为方程fnP1(z,f)=P2(z,f)的亚纯解,且P2(z,f)的次数不超过n，则有m(r,P1(z,f))=S(r,f)。

引理2[10]假设f是方程

af2+bff′+c(f′)2=d

的解,a,b,c,d是满足T(r,a)+T(r,b)+T(r,c)+T(r,d)=S(r,f)的亚纯函数,acd≢0，则有

下面给出定理1的证明。

假设f是方程(1)的超越整函数解,对式(1)求导得

(p′f+3pf′)f2+(qf″)′=(r′+rα′)eα+(s′-sα′)e-α。

上述方程和式(1)结合，并利用eα·e-α=1，有

f4[h1f2+h2ff′+h3(f′)2]=P4(z,f)，

(2)

其中:P4(z,f)表示f的微分多项式,其系数为多项式，degP4≤4,并且

(3)

令

κ=h1f2+h2ff′+h3(f′)2。

(4)

为了证明定理1，我们考虑以下两种情形:

情形1假设κ≡0。这样由式(4)得

[p′r-p(r′+rα′)]f+3prf′≡0 或者 [p′s-p(s′-sα′)]f+3psf′≡0。

因此,有

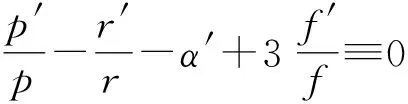
通过积分,可得

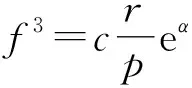
(5)

这里c为非零常数。

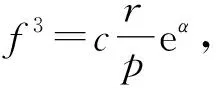
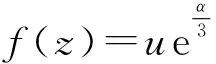
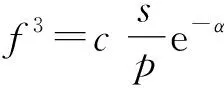
因此,情形1不会发生。

情形2假设κ≢0。对式(2)应用引理1，得到m(r,κ)=S(r,f)。再根据κ为整函数,所以T(r,κ)=S(r,f)。

若h1≡0，由式(3)得

p′r-p(r′+rα′)≡0 或者p′s-p(s′-sα′)≡0。

(6)

这样，根据p′r-p(r′+rα′)≡0,有p=creα,其中c为常数。考虑到p,r为多项式,α为非常数整函数,这是不可能的。所以,p′r-p(r′+rα′)≢0。

同理可证p′s-p(s′-sα′)≢0。因此h1≢0。又显然h3≢0。这样，再根据式(3)，有

h22-4h1h3=9p4(2rsα′+r′s-rs′)2。

(7)

若h22-4h1h3≡0，则有re2α=cs,这里c为非零常数。显然这是不可能的。因此，h22-4h1h3≢0，对式(4)应用引理2，得到

再把上式和式(3)结合,有

对上式进行积分,得

κ3r2s2=d(2rsα′+r′s-rs′)6p4，

(8)

其中常数d≠0。根据式(8)可知,存在多项式φ,使得rsp=φ3。这样,式(8)可以改写为

(9)

其中常数τ满足τ6=d。

现在,把式(9)代入式(4),有

上式意味着

(10)

和

(11)

成立,其中β为整函数。

然后，式(10)和(11)联立,得到

(12)

和

(13)

明显地,根据式(12)可得

(14)

再根据式(13)和(14),有

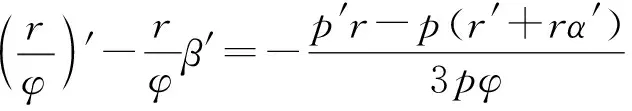
这样,上式蕴涵着

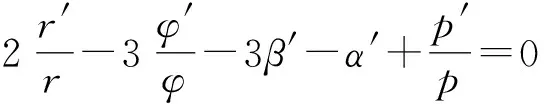
(15)

因为r,φ,p为多项式,α,β为整函数,由式(15),立即得到3β+α=ξ,这里ξ为常数。

对上式应用Borel定理,得

(16)

考虑到rsp=φ3,式(16)可以化为

(17)

根据v1,v2的定义,有

(18)

和

(19)

再利用式(17)中的第1个恒等式和第4个恒等式,有

τ6=-1，s=τ3e-ξr。

(20)

进一步,根据式(17)中的第2个恒等式和第3个恒等式,得

(21)

至此,根据3β+α=ξ以及式(18)—(21),我们有

(22)

对式(22)进行积分,立即得到s2(α′)3=cp2,这里c为非零常数。我们由此可以推知α是一个非常数多项式。同时,根据式(1),有ρ(f)<+∞。

根据假设条件，当p为常数时,根据s2(α′)3=cp2和式(20)得到p,r,s和α′均为常数。另外,再由式(17)得到q一定也是常数。

当r为常数时,由式(20),易知s也是常数。在这种情形下,可以假设p=t1φ3,α′=t2φ2，其中t1,t2为常数。下面我们证明φ也是常数。为此，假设多项式φ的次数为n,并且n≥1。于是,degp=3n，degα′=degβ′=2n。注意到s为常数,由式(17)中第2个恒等式和式(18)可得

9τ2p2φ2≡-q{[p″+(pα′)′]pφ+[p′+pα′][(pφ)′-β′pφ]}。

(23)

注意，式(23)右边多项式的次数等于degq+deg(pα′)+deg(β′pφ)≥11n,而其左边多项式的次数为8n,矛盾。这个矛盾表明n=0,也就是φ为常数。这样p,r,s和α′都是常数。利用式(17)可知q也是常数。

下面,给出f的表达式。为此，令

α=3az+b，

(24)

这里a≠0和b为常数。再由式(12)和(24)得

f(z)=c1eaz+c2e-az，

(25)

这里c1和c2为常数，且c1c2≠0。把式(25)代入式(1)，有

p(c13e3az+3c12c2eaz+3c1c22e-az+c23e-3az)+qa2(c1eaz+c2e-az)=re3az+b+se-3az-b。

对上式应用Borel定理，有

(26)

显然,由式(26)得到p2(c1c2)3=rs和3pc1c2+qa2=0。因此27prs+a6q3=0。这就完成了定理1的证明。

3 结 语

本文基于Yang等[7]和Gundersen等[8]对一类非线性微分方程整函数解的讨论，利用值分布论等基本理论，结合Clunie引理、Borel定理等，对一类非线性微分方程整函数解的具体形式进行了刻画。最后，我们提出一个问题，可供进一步研究。