噪声环境下语音信号增强方法和研究

李思嘉 赵婧 蔡树阳

摘要：基于小波去噪理论实现了阈值法语音增强算法，传统的软阈值法与硬阈值法在去噪处理上均有不足，经过软阈值法处理的语音信号与原始信号相比存在恒定误差，经过硬阈值法处理的语音信号不够光滑，且附加震荡的存在。在软硬阈值法的基础上提出了一种改进的软硬阈值折衷算法，提出的改进软硬阈值折衷算法和传统的阈值算法相比其适应性更优，克服了硬阈值函数不连续的缺点，减小了软阈值函数中估计小波系数与分解小波系数的恒定偏差，仿真结果说明，根据噪声信号的不同，通过修改式中系数，可得到比传统阈值法去噪更优的结果。

关键词：语音去噪；语音增强；阈值函数；小波变化

中图分类号：TP391文献标志码：A文章编号：1008-1739（2022）08-60-4

从带有噪声干扰的语音中提取纯净的语音为语音增强的目的，但是就目前的科技水平而言，从带有噪声干扰的语音中提取完全纯净的语音的可能性为零。近年来，随着科技的发展、生活质量的提高，人们对通信质量的要求也越来越高，为此必须增强系统抗噪声干扰的能力，尽可能地从带有噪声干扰的语音中提取纯净的语音，提高系统的处理性能。

语音信号由于受噪声的影响，且噪声的来源很复杂，可能与接收环境有关，也可能来自发送端或者设备内部处理信号产生的噪声等，这些噪声必然影响语音源信号的质量。如何从携带噪声干扰的语音中提取纯净的语音是语音增强的目的[1]。20世纪70年代中期Windrow B等[2]应用自适应相消法去噪，随后几年Limhe等[3]提出维纳滤波法，Boll[4]提出谱相减法，80年代初Maulay和Malpass[5]提出软判决噪声抑制法，80年代中期Ephraim和Malah[6]提出了基于最小均方误差（MMSE）短时谱语音增强法，而在80年代末，Paliwal[7]将卡尔曼滤波算法思想应用在语音增强算法中，进入90年代后，Ephraim[8]将信号子空间分解法应用于语音增强算法，而在2004年，Hu Yi和Loizou[9]将基于小波变换阈值函数的多窗口谱用于语音增强。经过多年的发展，语音增强算法已经逐步完善，已经变成整个语音系统中不可或缺的环节。

不同场景会产生不同的噪声，不同的噪声又有不同的特性，目前还没有一种适用于所有噪声类型的语音增强算法，因此需要结合不同的噪声提出与之相对应的语音增强算法。

1.1语音信号的特征

发声系统中不同位置发出的声源是不同的，因此语音信号是一个非平稳的时变随机过程，但人体中发声器官的变化有限，声带和声道处于一种相对稳定的状态，语音信号的基本特征保持不变，可在语音增强算法中用语音信号的短平稳性对其进行分析。

1.2噪声的特性

根据具体环境的不同，噪声的特性差异很大，有些噪声具有稳定性，有些噪声是非平稳的，依据环境和语音信号之间的联系，基本可以分为加性噪声和非加性噪声两大类，本文着重于对加性噪声的分析。

1.3语音增强算法的评判标准

1.3.1主观评价法

平均意见（Mean Opinion Score，MOS）得分法和判断韵字测试（Diagnostic Rhyme Test，DRT）得分法是2种主观评价的基本方法。

（1）MOS得分法

这种评价方法采用5级评价标准，需要大量测试者的评价数据，并且需要足够多的评测语音，最后去除所有测试者的平均评级等级即为最终的MOS得分，MOS评价标准如表1所示。

（2）DRT得分法

这种评价方法一般需要对大量测试者进行测试，对测试者播放多对相同韵母的同一韵字中的某音节，测试者根据所听到的音节选出相应的字，采取全部测试者的正确百分比做为DRT得分，DRT评价标准如表2所示。

1.3.2客观评价法

当人对语音质量敏感程度达不到算法要求时，主观评价方法就不再继续适用，客观评价法一般有2种：信噪比（SNR）和分段信噪比（SEGSNR）。

（1）SNR

2.1小波基和阈值选取

利用阈值法去噪的依据是语音信号和噪声信号在小波系数幅值上的不同，利用阈值法去噪，可以保留幅值较大的小波系数，这类系数一般为语音信号的小波系数，可将幅值小的小波系数减为零，这种小波系数一般为噪声信号的语音系数。

将实验仿真进行录音，并将其作为原始语音信号，通过awgn函数对原始语音信号加入高斯白噪声，将分解层数选为5，通过对软阈值法、硬阈值法以及改进的软硬阈值折衷算法的仿真，表明了改进算法的优势。依据主观评价法中的MOS得分法来评价阈值法的处理效果，仿真结果对比如图2所示。

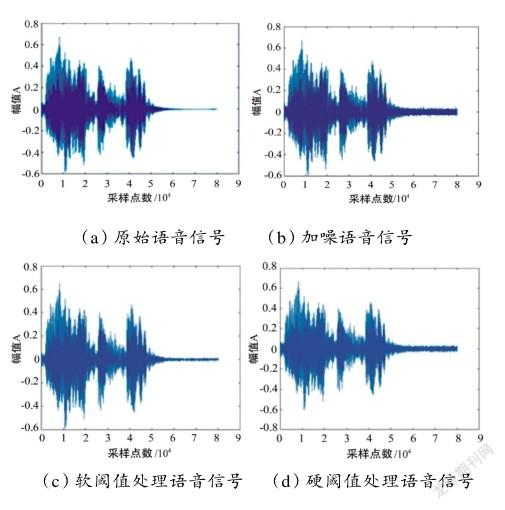
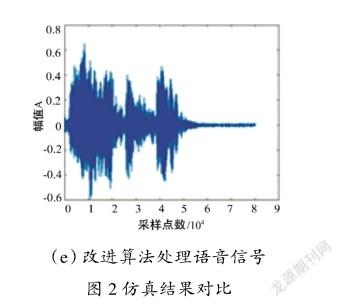
对比图像可知，改进的软硬阈值折衷算法对比软阈值法和硬阈值法更好地还原了原始语音信号，经过硬阈值法处理后的语音信号平滑度不够，而软阈值法与原始语音信号有所偏差。并且，通过仿真实验中播放处理后的语音信号，可以明显地感受到本文提出的改进折衷算法的处理效果要优于传统的软阈值法以及硬阈值法。

通过理论分析，在Matlab中对基于小波变换的软阈值法以及硬阈值法的语音增强算法予以实现，并提出了一种基于软硬阈值算法的折衷算法。提出了一种基于软硬阈值算法的折衷算法即改进软硬阈值折衷算法，仿真结果表明，和传统的阈值算法相比其适应性更优，克服了硬阈值函数不连续的缺点，减小了软阈值函数中估计小波系数与分解小波系数的恒定偏差，可以根据噪声信号的不同，通过修改式中系数，得到比传统阈值法去噪更优的结果。

参考文献

[1]赵力.语音信号处理[M].北京：机械工业出版社，2009.

[2] WIDROW B，GLOVER JR J R，MCCOOL J M，et al. Adaptive Noise Cancelling：Principles and Application[J].Proceedings of the IEEE，1975，63（12）：1692-1716.

[3] LIM J S，OPPENHEIM A V.All-pole Modeling of Degraded Speech[J].Acoustics，Speech and Signal Processing，IEEE Transactions on，1978，26（3）：197-210.

[4] BOLL S F.Suppression of Acoustic Noise in Speech Using Spectral Subtral[J].IEEE Transactions on ASSP， 1979，27（2）：113-120.

[5] MCAULAY R，MALPASS M.Speech Enhancement Using A Soft-decision Noise Suppression Filter[J]. Acoustics， Speech and Signal Processing，IEEE Transaction on，1980，28（2）：137-145.

[6] EPHRAIM Y，MALAH D.Speech Enhacement Using A Minimum-mean Square Error Short-time Spectral Amplitude Estimator[J].Acoustics，Speech and Signal Processing，IEEE Transactions on，1984，32（6）：1109-1121.

[7] KALMAN R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering，1960，82（1）：35-45.

[8] YARIV E， HARRY Van L.A Signal Subspace Approach for Speech Enhancement[J].IEEE Transactions.on Speech and Audio Processing，1995，3（4）：251-266.

[9] HU Y，LOIZOU P C.Speech Enhancement Based on Wavelet Thresholding the Multitaper Spectrum[J].IEEE Trans.on Speech and Audio Processing， 2004，12（1）：59-67.

[10]高迎東，王宏力，由四海，等.基于小波基函数选取与改进阈值函数的脉冲星信号去噪算法研究[J].电光与控制， 2020，27（4）：15-19.

[11]崔公哲，张朝霞，杨玲珍，等.一种改进的小波阈值去噪算法[J].现代电子技术，2019，42（19）：50-53.