W+衰变产生两个双重味介子
2022-07-04廖其力赵国平
廖其力, 邓 娅 , 余 艳, 赵国平
(1. 重庆移通学院 数理教学部, 重庆 401520; 2. 四川师范大学 物理与电子工程学院, 四川 成都 610068)
1 预备知识
1974年,Ding[1]发现了粲夸克(charm quark),证实了粲夸克的质量远大于当时已经发现上夸克(up quark)、下夸克(down quark)和奇异夸克(strange quark)这3类轻夸克的质量,是第一个远大于量子色动力学(Quantum Chromodynamics,QCD)能标ΛQCD的上重味夸克.紧接着,1977年在发现Υ(4S)的过程中证实了更重的底夸克(bottomquark)的存在[2].1983年发现传递弱相互作用的中间玻色子Z0和W±.1995年,费米实验室发现了标准模型预言的最后一个夸克——第六味夸克顶夸克(topquark)[3].由于t夸克的质量太大(约为172GeV),产生后便立即衰变,无法形成束缚态.这系列的发现标志着找到了一类更重的、参与强相互作用的基本粒子——夸克,同时也开辟了重味物理这一重要研究领域.
重夸克偶素态是指至少包含一个重夸克的重味介子,它们是由夸克、反夸克以及传递强相互作用的胶子组成的束缚态,夸克之间的相互作用是通过胶子来传递的强相互作用.由于粲夸克(mc≈1.4 GeV)和底夸克(mb≈4.9GeV)的质量都远大于强相互作用能标ΛQCD(约0.3GeV),所以重味强子的产生和衰变过程是可以用微扰量子色动力学(PerturbativeQuantumChromodynamics,PQCD)来描述的,其计算结果可以在实验上检验量子色动力学理论的正确性以及用来探索其他新物理机制存在的可能性.
在粒子物理的研究中,对重味夸克偶素态的研究在检验和发展标准模型中起着重要的作用,它也是粒子物理重要的研究领域之一.重味强子的产生与衰变过程主要有两种不同的理论:一种是微扰QCD的计算方法,即利用微扰PQCD或非相对论量子色动力学(NonrelativisticQuantumChromodynamics,NRQCD)等理论来进行计算重味强子产生和衰变的各种可能的机制[4],如夸克-反夸克湮灭、重夸克衰变、胶子-胶子熔合、中间玻色子衰变等机制;另一种是碎裂机制,它是根据费曼提出的部分子模型,利用具有普适性的碎裂函数(fragmentationfunction)来描述部分子碎裂生成强子的产生几率[5],其中部分子既可以是重夸克也可以是硬胶子.硬胶子的动量较大,远大于QCD能标ΛQCD.
本文研究传递弱相互作用的媒介子(中间玻色子W±弱衰变产生两个双重味介子)的遍举过程.人们之所以对重味强子的产生和衰变过程的研究具有浓厚的兴趣,是因为它们的产生或湮灭过程都包括多个特征能标,涉及到QCD的微扰与非微扰问题,有的特征能标是远大于强相互作用能标ΛQCD(约0.3GeV),因此产生或者湮灭的过程是可以微扰计算的.根据NRQCD理论,重味强子产生和衰变过程通常可因子化为两部分:一部分是硬胶子产生一对自由的重夸克的过程(即短程部分),由于其产生动量远大于QCD能标ΛQCD,该过程可用微扰QCD来完整计算;另一部分是自由夸克结合形成束缚态的“强子化”过程(长程部分),是QCD非微扰过程,即不能用QCD的费曼规则来进行微扰可算的,但可用格点QCD或QCD求和规则等来计算,也可以用位势模型等的非微扰方法来处理,由此发展而来的NRQCD理论就成了研究重夸克束缚态最强有力的理论工具之一[6-13].
2 中间玻色子W+衰变产生两个双重味夸克偶素态
由电荷共轭对称性可知,传递弱作用的媒介子W-和W+的衰变粒子具有完全共轭对称的物质与反物质的性质,故本文仅讨论W+衰变产生两个双重味夸克偶素态的遍举过程.
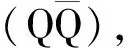
(1)
由图1,根据费曼规则,可将它们树图阶的振幅用以下形式表示
M=k(A1+A2),
(2)
其中
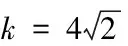
为弱耦合常数,mW为中间玻色子W+的质量,GF是费米弱衰变常数,αs为跑动耦合常数,VCKM是CKM矩阵元,Nc=3为QCD中夸克的颜色因子.
根据NRQCD理论,在非相对论条件下,非微扰矩阵矩阵元〈H|On|H〉可认为近似等于波函数的零点值ΨS(0),而后者又与径向波函数的零点值RS(0)有下列关系

A1=Tr
(3)
A2=Tr
γ(P1,q)]q=0,
(4)
对于标量束缚态的投影算子(s或s′=0;i=1,2),
(5)
对于矢量束缚态的投影算子(s或s′=1;i=1,2),
∏ν(pi,q)=
(6)
为了满足硬散射振幅的规范不变性,计算过程中束缚态的质量M取
1) 对于s=1、s′=0情况,即
的衰变宽度为
Γ(〉)=
(7)
(7)式中的振幅模方为

(8)
其中
2) 对于s=0、s′=1情况,即
的衰变宽度为
Γ(=
(9)
其中,振幅的模方表达式过于冗长,就不列举出来.
此处仅讨论费曼图中中间玻色子
(Ⅱ) 对于s=0、s′=1有
为了给出这4个过程的衰变宽度,采用以下数据[10]:
mW=80.399GeV,mc=1.35GeV,
mb=4.90GeV,|Vcb|=0.040 6,
|RGeV3,
|RGeV3,
|RGeV3.
根据以上参数可计算出W+衰变到两体双重味夸克偶素态的衰变宽度:
(10)
W+→J/Ψ+Bc的事例数为0.24个,
的事例数为3.3×10-6个,
的事例数为0.25个,
W+→Bc+Υ的事例数为3.6×10-2个.
如此小的事例数在强子对撞机这样复杂的背景是不可能观测到的.
