一类截断函数最优化问题的求解方法

左鑫怡, 蒋 毅*, 杨 岚

(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 四川师范大学 可视化计算与虚拟现实四川省重点实验室, 四川 成都 610066)

1 预备知识

本文考虑一类截断函数的最优化问题

min{fi(x),hi(x)},

(1)

其中x∈Rn是变量,

f0:Rn→R∪{+∞},

fi,hi:Rn→R,i=1,2,…,m

min

截断函数的最优化问题(1)在稀疏性正则化[1-4]、基于稳健估计的图像恢复[5]以及稳健回归[6-9]等方面都有广泛应用.

关于这类截断函数的最优化问题(1),许多学者考虑hi(x)=α(α为常数)的情况[1,10-11].Barratt等[10]首先利用截断函数的相关公式得到问题(1)的等价模型,然后运用启发式方法的思想进行求解.Liu等[11]提出了一种在低维空间下可得到全局最优化的通用算法.Ong等[1]首先利用截断函数的相关公式把问题(1)转化为DC问题的形式,然后利用求解DC问题的算法对其进行求解.本文考虑了hi(x)不是常数的情况,基于这些方法的启发,运用了启发式方法和ADMM方法的思想对问题(1)求解.

本文共分为三节:第一节为预备知识.第二节提出了截断函数最优化问题的两种计算方法,第一种方法首先对问题(1)中的模型进行等价替换,基于Barratt等[10]的研究,运用启发式方法的思想进行求解;第二种方法是在截断函数为非光滑函数的基础上,运用光滑逼近的思想使目标函数光滑化,然后运用ADMM方法[12]的思想进行求解.两种算法在满足一定的条件下都可以得到全局最优解.第三节应用了本文提出的两种计算方法求解经验风险最小化问题(ERM),给出数值实验结果,表明两种方法都有效.

在本文中,所有向量都是列向量,In表示n×n单位矩阵.

2 计算方法

本节主要介绍求解截断函数最优化问题(1)的两种计算方法:

第一种计算方法首先对问题(1)中的截断函数进行转换,得到其等价模型,然后在文献[10]的方法的启发下,运用启发式方法的思想进行求解.

第二种计算方法由于截断函数是一个不可微函数,因此应用光滑逼近的思想使截断函数光滑化,把问题(1)转化为光滑的优化问题,再运用文献[13-16]中ADMM算法的思想进行求解.

下面介绍第一种计算方法.首先给出引理2.1,运用该引理给出问题(1)的等价模型.

引理 2.1[8]函数min{fi(x),hi(x)}满足

min{fi(x),hi(x)}=

由引理2.1,可推出截断函数最优化问题(1)等价于下列问题

0≤λi≤1,i=1,2,…,m,

(2)

其中λi∈R(i=1,2,…,m)和x∈Rn是变量.

对于问题(2),当fi(x)可微时,可以用非线性规划方法求解,也可以用交替最小化求解.但在实际问题中发现,对λi实行非精确交替最小化效果更好.

首先,固定问题(2)中的λi,求解相应的最小化问题,将此时x的值记作xk.

然后对目标函数关于λ计算其梯度

gi=(▽λL(xk,λ))i=fi(xk)-hi(xk).

λ的迭代如下

λk=Π[0,1]m(λk-1-βsign(g)),

其中sign是符号函数,Π[0,1]m代表一种投影函数,其解析式为

(Π[0,1]m(z))

下面给出算法2.1.

算法 2.1步骤 1 初始化:

λ0≥0,β>0,ε>0.

1) 计算xk+1:通过求解下列问题,使其取最小值时x的取值记为xk+1,满足

gi=fi(xk+1)-hi(xk+1).

λk+1=Π[0,1]m(λk-βsign(g)).

算法2.1是一种下降算法,当固定λi时,问题(2)的目标函数值在每次迭代后都会减少,并且因为λi的取值是有限的,所以这个算法可以保证在有限的时间内终止.在实践中,发现算法2.1在一定的条件下可以达到全局最优解,而且在一些更复杂的情况下能实现得更好.

下面介绍第2种计算方法.

截断函数最优化问题(1)等价于下列问题

(3)

问题(1)中的截断函数满足等式

min{f1i(x),hi(x)}=

因此问题(1)等价于上述问题(3).由于绝对值函数是不可微的,所以本文利用绝对值函数

φ(x)=|x|

的光滑函数对其进行逼近,应用文献[17-19]的如下光滑函数:对任意p>0,

φ(x;p)=pln(ee

该光滑函数有如下性质.

引理 2.2[18]对任意p>0,光滑函数

φ(x;p):R→R+

满足:

φ(fi(x)-hi(x);p):=

pln(ee

因此,关于原问题(1)的光滑无约束优化问题定义为

(4)

引理 2.3问题(4)中定义的函数Φ(x;p)具有以下性质:

Φ(x;p1)<Φ(x;p2);

证明1)由引理2.2条件2),显然成立.

Φ(x;p)-Φ(x)=

|fi(x)-hi(x)|]=

plne

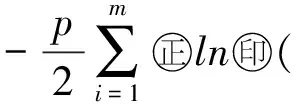
(5)

因此

0=ln1<
ln(ee
ln(1+1)=ln2.

(6)

由(5)式和(6)式可得

(7)

综上所述,引理2.3得证.

由引理2.2和2.3可知问题(4)是问题(3)的光滑逼近.

(8)

考虑增广拉格朗日乘子法[20],得

(9)

其中

Lβ(x,y,ω)=f0(x)+

下面介绍算法2.2.

算法 2.2步骤 1 初始化:

(y0,ω0)∈Rn×Rm,

p0>0,σ∈(0,1),

β>0,ε1>0,ε2>0.

xk+1:=argxminLβ(x,yk,ωk);

yk+1:=argyminLβ(xk+1,y,ωk);

ωk+1:=ωk+β(xk+1-yk+1);

4) 若

‖xk+1-yk+1‖<ε1

且

‖-β(yk-yk+1‖<ε1,

pt+1=σpt,

算法2.2是对变量进行交替最小化,若问题(7)中的目标函数满足文献[9]中的相关条件可得到全局最优解.

3 举例说明

在本节中,使用AMDR5 2.1GHz个人电脑,在MatlabR2019b环境下,应用算法2.1和算法2.2分别求解如下经验风险最小化(ERM)问题

其中x1,…,xN∈Rn,y1,…,yN∈Y,Y是输出空间,θ∈R是拟合参数,l:R×Y→R是损失函数,r:Rn→R是正则化函数.

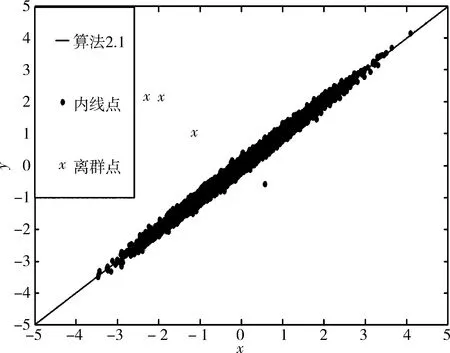
这里把l(xTiθ,yi)≥0.5的点(xi,yi)视为离群点,其余的视为内线点.在一些实际问题中ERM问题执行得很好,但是当数据中具有离群点时,它的性能就很会很差,因此本文考虑下列截断回归模型

(10)

下面对具有离群点的数据进行拟合.

然后随机选取5个点,将这5个点中的yi转化为-yi，

xi～N(0,1),yi=xi+0.1zi,
zi～N(0,1),i=1,2,…,N.

最后应用算法2.1和算法2.2求解截断回归模型(10).

(a) N=100时,算法2.1的计算结果

数值实验结果表明两种计算方法都有效,并且算法2.1的速度更快.