u-Matlis余挠模和G-整环的模刻画

王宇鑫, 王芳贵, 肖雪莲

(四川师范大学 数学科学学院, 四川 成都 610066)

众所周知,若R是整环但不是域,则R的商域K作为R-模不是有限生成的[1],但是K作为R-代数却可以是有限生成的.1951年,Goldman[2]在研究Hilbert环和Hilbert零点定理时,首先讨论了这种情况.几乎与之同时,Krull在文献[3]中也提到了具有这一性质的整环,并引起了专家学者们的重视,成为当年的研究热点之一.同年Artin和Tate在文献[4]中首次明确给出了该类整环的等价刻画:“(1)K是R的环有限扩张.(2)存在非零元a∈R,且每个素理想都包含a.(3)R仅有有限个极小素理想.(4)R仅有有限个素理想,且每一个素理想都是极大的.”直到1974年Kanplansky在其文献[5]中,才把Goldman和Krull讨论的这类整环正式命名为G-整环,同时给出了明确定义和重要性质.若商域K作为R-代数是有限生成的,则可由R中一个元素u生成,并在文中归纳总结了许多G-整环的相关性质.例如:“若R是G-整环,则介于其商域K与R之间的任意环T也是G-整环.”

希尔伯特零点定理是古典代数几何的基石,它给出了仿射空间中的点与多项式环的极大理想之间的一一对应关系,由此建立了代数和几何之间的关系,使得人们可以用交换代数的手段研究几何问题,而G-整环在刻画希尔伯特环时起到了重要作用.例如文献[5]中定义：如果交换环R中的每个G-理想都是极大的,那么R就是希尔伯特环.由此可见,G-整环及其相关问题有很重要的研究价值.

不难发现,尽管Kanplansky整理归纳了G-整环的许多性质,但这些都是环论性质的刻画.迄今为止,关于G-整环的结构缺乏模的刻画.回顾整环R称为Matlis整环,是指pdRK≤1.用Matlis余挠模可以较多地刻画Matlis整环[6-8].可以证明,若R是G整环,商域K=R[u-1],则有K=Ru,其中Ru表示R在乘法封闭集S={un|n≥0}上的分式环(引理3.5).此外,也证明了pdRRu≤1(命题3.2),这使得完全可以像刻画Matlis整环那样来刻画G-整环.为此,利用相关可除模概念[9-15]引入了u-Matlis余挠模的概念并对G-整环进行相应的模刻画,证明了G-整环就是Matlis整环.

1 u-可除模和u-内射模

以下恒设R是交换环,u∈R是非零因子.

定义 1.1设M是R-模.

1) 若对任何x∈M,存在非负整数n,使得unx=0,等价地,Mu=0,则M称为u-挠模.

2) 若由ux=0,x∈M,能推出x=0,等价地,自然同态ϑ:M→Mu是单同态,则M称为u-无挠模.

3) 若M=uM,等价地,对任何x∈M,恒存在y∈M,使得x=uy,则M称为u-可除模.

记录以下的基本事实,以备引用时之需要.

例 1.21)u-挠模的子模与商模都是u-挠模.

2)u-无挠模的子模仍为u-无挠模.

3)u-挠模的直和是u-挠模,于是由1)还有偏序集上的u-挠模的正向极限还是u-挠模.

4) 设M是u-挠模,N是任何模,则M⊗RN是u-挠模.更一般地,对任何n≥1,是u-挠模.

5)u-无挠模的直积是u-无挠模.

6)u-可除模的商模,直和与直积都是u-可除模.

7) 设A、B是模M的u-可除子模,则A+B也是M的u-可除子模.

8) 对任何模M,M中有一个最大的u-可除子模.

9) 任何Ru-模作为R-模既是u-无挠的,又是u-可除的.

10) 模M是u-可除模,当且仅当

当且仅当对任何n≥1,有

11) 设X是任何模,M是u-无挠模,则HomR(X,M)是u-无挠模.

12) 若T是u-挠模,M是u-无挠模,则

HomR(T,M)=0.

设M是R-模,令

Tu(M)={x∈M|存在非负整数n,

使得unx=0},

则Tu(M)称为M的完全u-挠子模.

例 1.3下面的事实也是显然的:

1)M是u-挠模当且仅当Tu(M)=M.

2)M是u-无挠模当且仅当Tu(M)=0.

3)M/Tu(M)总是u-无挠模.

4) 设M是u-无挠模,则Mu/M是u-挠模.

5) 若M既是u-无挠模,又是u-挠模,则M=0.

设I是R的理想.若I包含了一个un,则称I是u-理想.如文献[16],称R-模E为u-内射模,是指对R的任何u-理想I,有

例 1.4下面的事实也是显然的:

1) 自然地,内射模是u-内射模.

2)u-内射模是u-可除模.

4) 设0→A→B→C→0是正合列,且A、C都是u-内射模,则B也是u-内射模.

设M是R-模,令

u(M)={x∈E(M)|存在自然数n,

使得unx∈M},

则u(M)是E(M)中包含M的子模,且

Tu(E(M))⊆u(M),

u(M)称为M的u-可除包络.当I是R的u-理想时,有R⊆u(I).

命题 1.5对R-模E,以下各条等价:

1)E是u-内射模.

2) 对R的任何u-理想I,任何同态f:I→E能扩张到R上.

3) 设A是R-模B的子模,f:A→E是同态.若B/A是u-挠模,则f可以扩张到B.

4) 对任何u-挠模C,

5) 设A是R-模,f:A→E是同态,则f可以扩张到u(A).

证明由文献[16]的定理3.3,令S={un|n≥0}即得.

命题 1.6对u-无挠模L,以下各条等价:

1)L是u-内射模.

2)L是u-可除模.

3)u(L)=L,即由unx⊆L(其中x∈E(L),n是自然数),能推出x∈L.

证明由文献[16]的定理3.4,令S={un|n≥0}即得.

推论 1.7每个Ru-模作为R-模是u-内射模.

证明由例1.2与命题1.6即得.

下面证明本节的主要定理.

定理 1.8每个u-可除模是一个u-内射模的商模.

为证明定理1.8,姑且把u-内射模的商模称为hu-可除模.

例 1.9容易得到的hu-可除模的基本性质如下:

1)u-内射模自然是hu-可除模,于是hu-可除模的商模仍然是hu-可除模.

2) 由于u-内射模的直积都是u-内射模,因而hu-可除模的直积是hu-可除模.

3) 若A、B是模M的hu-可除子模,则A+B也是M的hu-可除子模,从而由Zorn引理可以得到任何模M有一个极大的hu-可除子模.再由2)得到任何模M有一个最大的hu-可除子模.

命题 1.10设D是R-模,则以下各条等价:

1)D是hu-可除模.

3)D是一个u-无挠的u-可除模的商模.

4) 对任何x∈D,存在同态g:Ru→D,使得g(1)=x.

证明1)⟹2) 由于D是hu-可除模,故存在满同态E→D,其中E是u-内射模.考虑下面的交换图

HomR(Ru,E)→HomR(Ru,D)↓↓HomR(R,E)→HomR(R,D)

由于Ru/R是u-挠模,E是u-内射模,故左边的垂直箭头是满同态.由于R是自由模,所以下行的水平箭头也是满同态.因此,右边的垂直箭头是满同态.于是有0→HomR(Ru/R,D)→HomR(Ru,D)→HomR(R,D)→0是正合列.

2)⟹3) 显然,D≅HomR(R,D)是HomR(Ru,D)的同态像,且HomR(Ru,D)是Ru-模,从而作为R-模是u-无挠和u-可除的.

3)⟹1) 由命题1.6,u-无挠的u-可除模是u-内射模,故D是hu-可除模.

2)⟹4) 设λ:R→Ru是包含映射.对任意的x∈D,令

f:R→D,f(r)=rx,

则

f∈HomR(R,D).

由假设

λ*:HomR(Ru,D)→HomR(R,D)

是满同态,故存在

g∈HomR(Ru,D)

使得λ*(g)=f,即f=gλ,此时

g(1)=f(1)=x.

4)⟹2) 对任意的f∈HomR(R,D),令f(1)=x.由条件,存在g∈HomR(Ru,D),使得g(1)=x.对任意的r∈R,g(r)=rg(1)=rx=rf(1)=f(r),所以g|R=f,故0→HomR(Ru/R,D)→HomR(Ru,D)→HomR(R,D)→0是正合列.

hn(u-n)=xn(x0=x),

则有hn是同态,且hn是hn-1的扩张.a∈Ru,则存在n,使得a∈Rn.令h:Ru→D,使得h(a)=hn(a),则h是同态且是h0的扩张.由此有

h(1)=h0(1)=x.

由命题1.10,D是hu-可除模.

由于u-可除模与hu-可除模的一致性,以下不再说hu-可除模.

命题 1.11对模D,以下各条等价:

1)D是u-可除模.

2) 对任何n>0,

证明1)⟹2)n=1是显然的.设n>1,考虑正合列0→Run-1/Run→R/Run→R/Run-1→0,有

Run-1/Run≅R/Ru

和归纳法即得所证.

2)⟹1) 取n=1即满足要求.

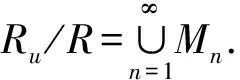
0=M0⊆M1⊆M2⊆…⊆Mn⊆…

是Ru/R的子模的连续升链.对n≥1,显然有

Mn/Mn-1≅Ru-n/Ru-(n-1)≅R/Ru.

因此,有

由文献[1]的引理11.7.2有

命题 1.12设M是R-模.

1) 若对任何u-可除模D,有则pdRM≤1.

2) 若M是u-挠模,且有pdRM≤1,则

证明1) 设X是任何模,取正合列0→X→E→D→0,其中E是内射模,故D是可除模,从而D是u-可除模.由正合列0=有因此,有

pdR(M)≤1.

2 u-Matlis余挠模和u-平坦模

定义 2.1设L是R-模,若

则L称为u-Matlis余挠模.

命题 2.2设D是u-可除模,则D是u-Matlis余挠模.特别地,u-内射模是u-Matlis余挠模.

证明由正合列与命题1.11即得.

定义 2.3设M是R-模.若M无非零的u-可除子模,则M称为u-约化模.

命题 2.4对模M,以下各条等价:

1)M是u-约化模.

2) 对任何u-可除模D,HomR(D,M)=0.

证明1)⟹2) 设f∈HomR(D,M),于是f(D)是M的u-可除子模.由于M是约化模,故f(D)=0.因此,f=0,从而得到

HomR(D,M)=0.

2)⟹3) 这是平凡的.

3)⟹1) 若M不是u-约化模,则M有非零的u-可除子模D,由命题1.10,存在同态f:Ru→D,f≠0.设i:D→M是包含同态,则λf:Ru→M是非零同态,这与假设矛盾,故M是u-约化模.

命题 2.51)u-约化模的子模是u-约化模.

2)u-约化模簇的直积还是u-约化模,从而u-约化模簇的直和也是u-约化模.

证明1) 显然.

2) 设{Mi}是一簇R-模,由自然同构

HomR(RHomR(Ru,Mi)

并引用命题2.4即得.

引理 2.6设M是R-模,则

Tu(M)≅

且有正合列0→Tu(M)→M→Ru⊗RM→(Ru/R)⊗RM→0,从而M是u-无挠模当且仅当

M≅R⊗RM,Mu≅Ru⊗RM,

于是得到

Tu(M)≅

和所需正合列.

命题 2.71) 设0→A→B→C→0是正合列.若B是u-Matlis余挠模,C是u-约化模,则A是u-Matlis余挠模.

2) 设A是u-挠模,则对任何模X,HomR(A,X)是u-约化的u-Matlis余挠模.特别地,HomR(Ru/R,X)是u-约化的u-Matlis余挠模.

3) 设D是u-可除模,则有正合列0→M→E→D→0,其中E是u-无挠的u-可除模,M是u-约化的u-Matlis余挠模.

4) 设M是u-无挠模,则既是u-约化模,又是u-Matlis余挠模.

证明1) 由于C是u-约化的,由命题2.4,HomR(Ru,C)=0.又由于B是u-Matlis余挠模,故由正合列0=HomR(Ru,C)→得到

即A是u-Matlis余挠模.

2) 由于A是u-挠模,故Ru⊗RA=0,且有

(Ru/R)⊗RA=0.

由相伴同构定理,有

HomR(Ru,HomR(A,X))=0.

HomR(A,X))≅

现在考虑一般情形.设0→X→E→Y→0是正合列,其中E是内射模,于是有正合列0→HomR(A,X)→HomR(A,E)→HomR(A,Y),由前面所述HomR(A,Y)是u-约化模.同理

HomR(A,E))≅

3) 令

M=HomR(Ru/R,D),E=HomR(Ru,D).

由命题1.10的2)即得.

4) 由引理2.6,有正合列0→M→Ru⊗RM→(Ru/R)⊗RM→0.由于M与Ru⊗RM都是u-无挠模,Ru/R是u-挠模,故有

HomR(Ru/R,M)=0,

且

HomR(Ru/R,Ru⊗RM)=0.

由于Ru⊗RM还是u-内射R-模,因此有

于是有同构

HomR(Ru/R,(Ru/R)⊗RM).

在2)中取

A=Ru/R,X=(Ru/R)⊗RM,

命题 2.8设M是u-约化模.

1)M是u-Matlis余挠模当且仅当

M≅

2) 若M是u-无挠模,则有正合列0→M→C→E→0,其中E是u-无挠的u-可除模,C是u-约化的u-Matlis余挠模.

证明1) 由于M是u-约化模,故

HomR(Ru,M)=0,

于是有正合列0→M→因此,M是u-Matlis余挠模当且仅当

M≅

2) 在1)的证明中,记

C=

并引用命题2.7即得.

定义 2.9设M是R-模.若对任何u-Matlis余挠模C,有则M称为u-平坦模.

投射模显然是u-平坦模,Ru显然也是u-平坦模.更一般地,投射Ru-模也是u-平坦R-模.由于余挠模是u-Matlis余挠模,故u-平坦模一定是平坦模.

定理 2.10若M是平坦模,且对任何平坦的u-Matlis余挠模C,有则M是u-平坦模.

证明对任何u-Matlis余挠模C,由于平坦模类与余挠模类构成是遗传和完全的余挠理论,故有正合列0→X→G→C→0,其中G是平坦模,X是余挠模,且有

于是有G还是u-Matlis余挠模.由假设

推论 2.11设M是u-平坦模,则

Mu=Ru⊗RM

是投射Ru-模,从而对任何u-Matlis余挠模C,以及任何k>0,有

定理 2.12设R是整环,P是投射模,F是P的u-平坦子模,则F是投射模.

证明设D是u-可除模,证明

3 G-整环的模刻画

引理 3.1设R是任何环,a1,a2,…,an是R中的非零元素序列,F是以x0,x1,…,xn为基底的自由模.令

yn=xn-an+1xn+1,n=0,1,2,….

若n≥1,y=r0x0+r1x1+…+rnxn∈F,则

…+r1a2…an+r0a1…an)xn,

其中j=k时,视aj+1aj+2…ak=1.

证明当n=1时,y=r0x0+r1x1=r0y0+(r1+r0a1)x1,故断语为真.设n>1,并令

z=r0x0+r1x1+…+rn-1xn-1,

由归纳假设有

从而有

y=z+rnxn=

a

命题 3.2设u∈R是非零非单位元素,则Ru是由

生成的R-模,且pdRRu≤1.

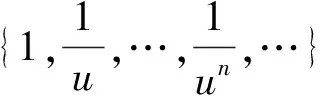
令P=ker(φ),并令

yn=xn-uxn+1,n≥0.

因此,yn∈P.另一方面,设y∈P,可记

y=r0x0+r1x1+…+rnxn.

由

有

r0un+r1un-1+…+rn-1u+rn=0.

若n=0,则y=r0x0.由于φ(y)=r0=0,有y=0.设n≥1,由引理3.1有

y=r0y0+(r1+r0u)y1+(r2+r1u+r0u2)y2+

…+(rn-1+rn-2u+…+r0un-1)yn-1,

故P是由y0,y1,y2,…,yn,…生成的子模.由文献[1]中定理3.10.20(1),P是自由模,从而有

pdRRu≤1.

引理 3.3设R是整环,u∈R,u≠0,则

R[u-1]=Ru.

α=f(u-1)∈R[u-1],

故

Ru⊆R[u-1].

反之,设α∈R[u-1],则可记

α=r0+r1u-1+…+rnu-n,ri∈R.

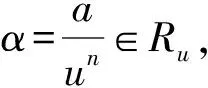
a=r0un+r1un-1+…+rn,

故

R[u-1]⊆Ru,

于是得到

R[u-1]=Ru.

回顾整环R称为G-整环,是指其商域K作为R-代数是有限生成的.在文献[5]中还指出,K可以由一个元素α∈K生成,即K=R[α].记

由于

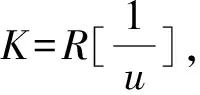
推论 3.4设R是G-整环,则存在u∈R,u≠0,使得K=Ru.

引理3.5设R是G-整环,且K=R[u-1],则任何非零理想都是u-理想.

证明设I是R的非零理想,则存在a∈I,a≠0.由于

则可记

其中r∈R.于是

un=ra∈I,

即I是u-理想.

引理 3.6设R是整环.则每个R-模是Matlis余挠模当且仅当R是域,即R=K.

证明设N是R-模.由假设,N是Matlis余挠模,故

于是K是投射模,且

rankR(K)=1,

故K是有限生成R-模,从而有K=R.

定理 3.7设R是G-整环,则R是Matlis整环.

证明记K=R[u-1],则K=Ru.由命题3.2,pdR(K)≤1,故R是Matlis整环.

设N是R-模,则每个Ru-同态f∈HomRu(K,N)也可以看成一个R-同态,故有自然嵌入:

θ:HomRu(K,N)→HomR(K,N).

引理 3.8设R是整环,u∈R是非零非单位元素.设N是Ru-模,则有:

2)N是Matlis余挠R-模当且仅当N是Matlis余挠Ru-模.

证明1) 先来证明

HomRu(K,N)=HomR(K,N),

即证明每个R-同态f:K→N可以作成一个Ru-同态.由于Ku=K,故K也是Ru-模.对任何x∈K,k≥0,有

由于N是Ru-模,故有

从而对任何r∈R,有

故f还是Ru-模同态,从而得到

HomR(K,N)=HomRu(K,N).

设0→N→E→X→0是Ru-模的正合列,其中E是内射Ru-模.由文献[1]的习题3.16,E也是内射R-模,于是有下面的两行是正合列的交换图:

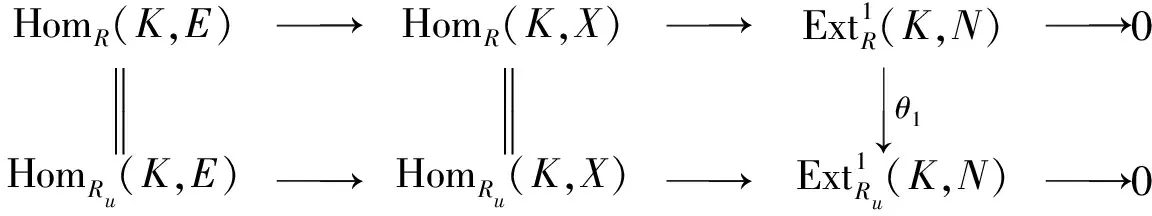
HomR(K,E)→HomR(K,X)→Ext1R(K,N)→0θ1↓HomRu(K,E)→HomRu(K,X)→Ext1Ru(K,N)→0

其中θ1是左边交换方图的诱导同态.由五项引理,θ1是同构.

2) 由1)即得.

下面用u-内射模、u-Matlis余挠模来刻画G-整环.

定理 3.9设R是整环,且R≠K,则以下各条等价:

1)R是G-整环.

2) 存在非零非单位元素u∈R,使得每个u-内射模都是内射模.

3) 存在非零非单位元素u∈R,使得每个u-无挠的u-内射模都是内射模.

4) 存在非零非单位元素u∈R,使得每个u-Matlis余挠模都是Matlis余挠模.

5) 存在非零非单位元素u∈R,使得每个u-无挠的u-Matlis余挠模都是Matlis余挠模.

证明1)⟹2) 设E是u-内射模,I是R的任意非零理想.根据引理3.5,I也是R的u-理想.再由命题1.5有任何同态f:I→E能扩张到R上,故任何理想I到E的同态都能扩张为R到E的同态,则E是内射模(Baer准则).

2)⟹3) 这是平凡的.

3)⟹1) 记S1=R-0,K=RS1,即K是R商域.S2={un|n≥0},Ru=RS2.设I是u-无挠的u-可除模.由命题1.6知,I是u-内射模.再由假设可得I是内射模亦是可除模,由此得到每一个u-可除模是可除模,则有S1⊆S2,K⊆Ru,所以K=Ru,R是G-整环.

1)⟹4) 显然,R是G-整环,则由推论3.4,存在u∈R,u≠0,使得K=Ru,故每个u-Matlis余挠模都是Matlis余挠模.

4)⟹5) 这是平凡的.

5)⟹1) 设N是任意Ru-模,则N作为R-模是u-无挠且u-可除的.根据命题2.2知,任意u-可除模是u-Matlis余挠模,故N为u-无挠的u-Matlis余挠模,由假设可知N是Matlis余挠模.再由引理3.6,有Ru是整环,每个Ru-模N是Matlis余挠模当且仅当Ru是域,即Ru=K,所以R是G-整环.