基于设计地震动的覆盖层场地空间自由场构建
2022-07-04宋志强刘云贺
韩 鲁,宋志强,王 飞,刘云贺
(西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西,西安 710048)
地震动输入[1−4]是结构地震响应分析和抗震安全[5−7]研究的前提。目前,地震动输入多是在均质基岩组成的半无限地基中构建地震动空间自由场[8−10]。对于覆盖层场地,由于地震波经过基岩-覆盖层界面时的透射、到达覆盖层地表时的反射以及土层介质阻尼造成的幅值衰减作用,使得覆盖层场地地震动场明显区别于均质基岩地基自由场[11]。开展基岩-覆盖层场地地震动特征及空间自由场构建研究,对于覆盖层地基地震动输入及其上建筑物地震响应研究具有重要意义。
目前,关于场地效应的研究中,垂直入射假定应用最为广泛[12−13]。Mehdi等[14]假定地震波从基岩垂直入射至地表,使用改进的直接有限元法对高拱坝-水库-地基进行了非线性地震分析。但在近场地震中,地震波往往是以一定角度斜入射至地表[15−18]。孙纬宇等[19]研究了河谷地形在SV波斜入射下的场地效应,结果表明:斜入射条件下场地效应受入射角影响且与垂直入射有明显差异。García等[20]研究表明:SV波和P波斜入射下拱坝的地震反应明显大于垂直入射的地震反应。同时,大量的研究将场地简化为均质半无限弹性空间[21−23],以此推导地震波在场地中的传播规律并分析场地效应,如黄博等[24]基于半无限弹性空间研究SV波斜入射形成的动应力路径;Pelli等[25]采用线弹性模型研究了具有空腔的半平面空间在SV波作用下的应力场和变形场。但由于覆盖层[26]和基岩的材料力学特性存在明显差异,将基岩-覆盖层场地视为均质半无限弹性空间并不合理,根据场地条件分别赋予覆盖层和基岩不同的材料参数,考虑地震波经过基岩-覆盖层界面时的透射、到达覆盖层地表时的反射[27]更符合实际。地震波在覆盖层传播时会发生幅值衰减,将场地视为弹性介质会忽略这一因素,因而需引入新的参数以考虑由覆盖层引起的幅值衰减[28]。此外,当地震波组合斜入射时,由于场地不同空间点波场组合叠加方式不同,场地地震动具有空间非一致性[29],何卫平等[30]考虑地震波组合效应获得了具有空间差异性的均质基岩场地自由场,并研究场地地震动的空间非一致性对重力坝响应的影响。目前,尚未见关于基岩-覆盖层场地地震动空间自由场构建及空间非一致特性研究。
因此,本文提出了一种基于覆盖层地表设计地震动的基岩-覆盖层场地空间差异自由场构建方法。首先建立了覆盖层场地空间任一点地震动与入射SV波和P波的关系式,其次根据覆盖层地表控制点两向设计地震动和入射角获得入射SV波和P波的时程,进而分析地震波在覆盖层场地经多次反射的传播路径,引入阻尼比考虑衰减作用,最终构建了基岩-覆盖层场地空间自由场,并采用美国La Cienega场地实际台阵记录进了验证。
1 SV波、P波组合斜入射下的自由场
1.1 入射波在弹性分界面的透射及反射
由于SV波和P波在覆盖层和基岩的传播速度不同,其在覆盖层和基岩的弹性分界面上均会产生透射SV波、透射P波、反射SV波和反射P波。另一方面,当SV波和P波传播到覆盖层自由表面时,由于自由表面以上不存在传播介质,因此只会产生反射波SV波和P波。SV波和P波在弹性分界面和自由表面的透射和反射关系如图1。根据弹性分界面的位移和应力连续条件及斯奈尔定律,可以得到SV波在弹性分界面的透射和反射系数的矩阵如式(1),P波在弹性分界面的透射和反射系数的矩阵形式如式(2)。

图1 SV波和P波的透射和反射关系Fig. 1 Relationship between transmission and reflection of SV and P waves
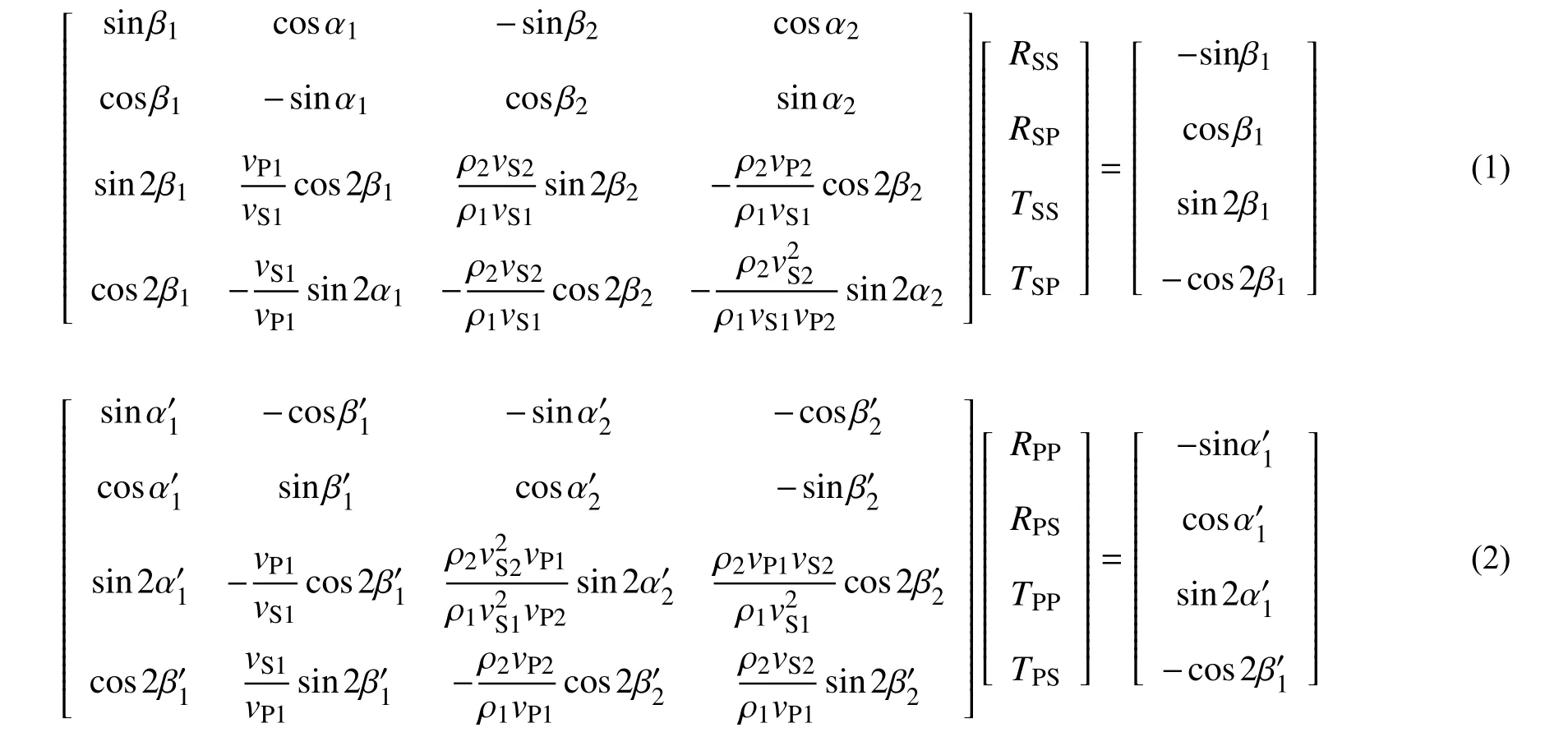
式中:ρ1和ρ2分别为基岩和覆盖层的密度;νS1和νP1分别为SV波和P波在基岩中的传播速度;νS2和νP2分别为SV波和P波在覆盖层中的传播速度。SV波入射时,β1和α1分别SV波和P波在基岩中的反射角;β2和α2分别SV波和P波在覆盖层中的反射角;RSS、RSP、TSS、TSP分别为反射SV波、反射P波、透射SV波、透射P波的系数。P波入射时,符号表示与SV波入射相似,不再赘述。
1.2 入射波在自由表面的反射
根据覆盖层自由表面应力为零的边界条件及斯奈尔定律可以得到SV波和P波在自由表面的反射系数如式(3)。
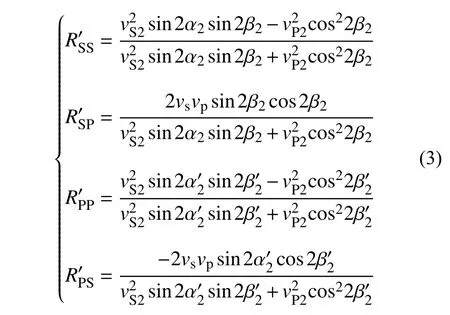
1.3 自由场任意空间点位移分量表达
地震波在弹性分界面和自由表面的每一次反射都会产生两种反射波,随着反射次数的增多,反射波的数量也呈几何式上升。对于任意空间点,经过该点的反射波有无数条,每一条对该点地震动的贡献程度不同,随着反射次数的增加,反射波幅值逐渐减小,当反射次数超过某一数值时,反射波幅值减小至可以忽略不计。在确定入射波信息和入射角后,根据空间点的位置和波速计算到达该点的所有反射波及其延时效应,由地震波的叠加理论可以获得空间点的位移分量。设入射P波的时程为g(t),入射SV波的时程f(t)。
若空间点位于覆盖层自由表面,则其反射次数只能为偶数,图2表示SV波入射时到达自由表面空间点的地震波传播路径。以S和P分别表示SV波和P波。当反射次数为0时,有SS和SP 2条地震波;当反射次数为2时,有SSSS、SSSP、SSPS、SSPP、SPSS、SPSP、SPPS、SPPP8条地震波;以此类推,当反射次数为m时,由SV波入射产生的一系列地震波有2m+1条,其中到达空间点的P波和SV波各2m条。P波入射的情况与SV波入射相似,在此不再赘述。由图1和图2中的几何关系可以得到自由场任意空间点位移分量的表达式,如式(4)和式(5)。

图2 SV波入射时自由表面空间点的地震波传播路径Fig. 2 Propagation path of seismic waves at a point on free surface when SV wave is incident


若空间点位于覆盖层内,则其反射次数为自然数。图3表示SV波入射时到达覆盖层内空间点的地震波传播路径。可以看出,反射次数为偶数代表反射波从空间点下方入射,反射次数为奇数代表反射波从空间点上方入射。由图3中的几何关系可以得到自由场任意空间点位移分量的表达式,如式(6)和式(7)。

图3 SV波入射时覆盖层内空间点的地震波传播路径Fig. 3 Propagation path of seismic waves at a point in overburden when SV wave is incident

2 基于设计地震动的自由场构建
2.1 入射SV波、P波时程的求解
目前大多数研究是直接采用地表地震动作为入射波进行输入,而基于设计地震动的自由场构建首先要由控制点时程(即设计地震动)反演入射P波和SV波的时程和入射角等信息。以往的研究大多依据地表地震动水平分量进行一维反演(即取基岩入射波峰值加速度为地表峰值加速度的一半)输入。显然,根据覆盖层表面地震动进行二维反演获得入射SV波和P波的信息,再根据SV波和P波得到空间自由场,进而完成地震动波动输入更为合理。该过程可保证控制点时程与设计地震动在水平和竖直两向均是一致的。由式(4)和式(5)可以得到地表的两向设计地震动与入射SV波和P波的关系式,如式(8)和式(9):

在时域上难以直接由式(8)和式(9)求入射波时间历程f(t)和g(t),但通过傅里叶变化可将式(8)和式(9)转化为频域的方程:

式中:h(ω)和v(ω)分别为水平向时程h(t)和竖直向时程v(t)的傅里叶变换;f(ω)和g(ω)分别为SV波时程f(t)和P波时程g(t)的傅里叶变换。应用式(10)和式(11)即可求解出f(ω)和g(ω),再根据傅里叶逆变换即可获得SV波和P波的时间历程。
2.2 入射角度的求解
入射角对地震动的影响很大,确定合理的入射角是构建自由场的另一重要步骤。在实际地震中,水平向地震动一般受SV波影响较大,竖直向地震动一般受P波影响较大,同时P波往往相较SV波更早到达地面。因而可以通过地表水平向地震动和竖直向地震动的平均幅值的比值来确定SV波和P波的主要贡献时段,并在SV波和P波的主要贡献时段内分别确定SV波和P波的入射角,如图4。
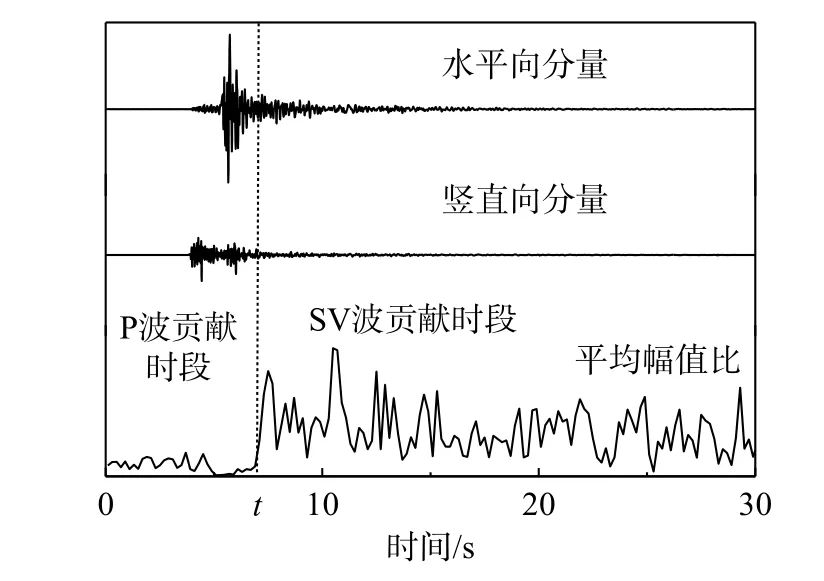
图4 两向地震动的平均幅值比Fig. 4 Average amplitude ratio of two directional ground motions
平均幅值的计算如式(12)所示。

式中:将地震持续时间划分为N段时窗;Mi为时窗i的平均幅值;l为一个时窗内数据点的个数;T1、T2分别为每个时窗的起始和终止时刻;a(t)为加速度时程。
在SV波主要贡献时段,记水平向的地震动平均峰值(正负峰值绝对值的平均)为PSV-h,竖直向地震动平均峰值为PSV-v。在P波主要贡献时段,记水平向的地震动平均峰值为PP-h,竖直向地震动平均峰值为PP-v。则SV波和P波入射角可用式(13)和式(14)表示:
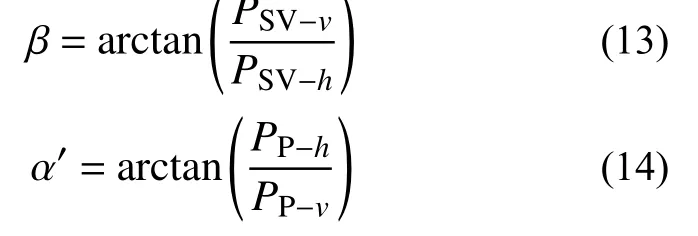
2.3 地震波幅值衰减的影响
地震波在覆盖层中传播时,覆盖层有着明显的隔震作用,即地震波在覆盖层中传播相较基岩幅值有明显的衰减,并且对于高频部分,其幅值衰减更加明显。为了考虑覆盖层对地震波的衰减作用,假设覆盖层是具有粘性的介质,引入阻尼比,地震波在传播过程中的衰减作用[31]可用式(15)表示:

式中:A为考虑衰减后的幅值;A0为未考虑衰减的幅值;z为地震波在覆盖层中传播路径的长度;k反映随着传播路径长度的增大,振幅衰减的快慢程度,可用式(16)表示:

式中:v为入射波速;λ为阻尼比;ω为入射波的频率。不同覆盖层对地震波衰减的影响不同,故应采取合适的阻尼比来考虑覆盖层的衰减作用。阻尼比由试验或根据场地条件和工程经验确定,可在一定合理的范围据经验进行调整,以减小土体非线性、不均匀性等因素的影响。此外,地震波的频率组成是复杂的,因而需将地震波时间历程利用傅里叶变换转化为频谱,然后将每一频率下的k依次求出并代入式(15)得到该频率衰减后的幅值,再利用傅里叶逆变换即可求得衰减后的时间历程。式(16)也可以简化处理,由于实际地震中与场地频率接近的部分受场地的影响较大,因而可以取ω为场地的固有频率。
2.4 自由场构建流程
由式(13)和式(14)获得SV波和P波的入射角,由式(10)和式(11)及傅里叶变换和逆变换获得入射SV波和P波的时间历程,根据式(4)~式(7)即可得到任意空间点在SV波、P波组合斜入射作用下的地震动。图5为本文计算方法的流程图。

图5 本文计算方法的流程图Fig. 5 Flow chart of calculation method in this paper
3 自由场构建算例分析
3.1 覆盖层场地实测地震动的选取及计算模型
为了验证本文方法的准确性,以一台阵的实测地震动作为设计地震动构建自由场并与其它测点对比分析。La Cienega台阵位于美国南加州,该台阵地表海拔为26 m,在地下0 m、18 m、100 m、252 m共布置4个测点,根据地表(0 m)处的实测地震动获得入射SV波和P波,由入射波建立的自由场与其他测点的实测数据进行对比验证本文方法的可行性。La Cienega台阵地表125 m深度内的横波波速VS和纵波波速VP分布如图6所示,由该台阵沿深度方向的剪切波速可认为100 m深度下的地质为基岩[32]。其100 m深度内的等效剪切波速为490 m/s,等效压缩波速为1626 m/s,土层饱和密度为1.99 g/cm3;100 m深度下的剪切波速为650 m/s,压缩波速为1900 m/s,土层饱和密度为2.10 g/cm3。该台阵在一次地震事件中0 m处的实测位移时间历程如图7,依据式(13)和式(14)确定SV波入射角为14°,P波入射角为57°。

图6 La Cienega台阵VS和VP沿深度的分布Fig. 6 La Cienega array VS and VP distribution along depth
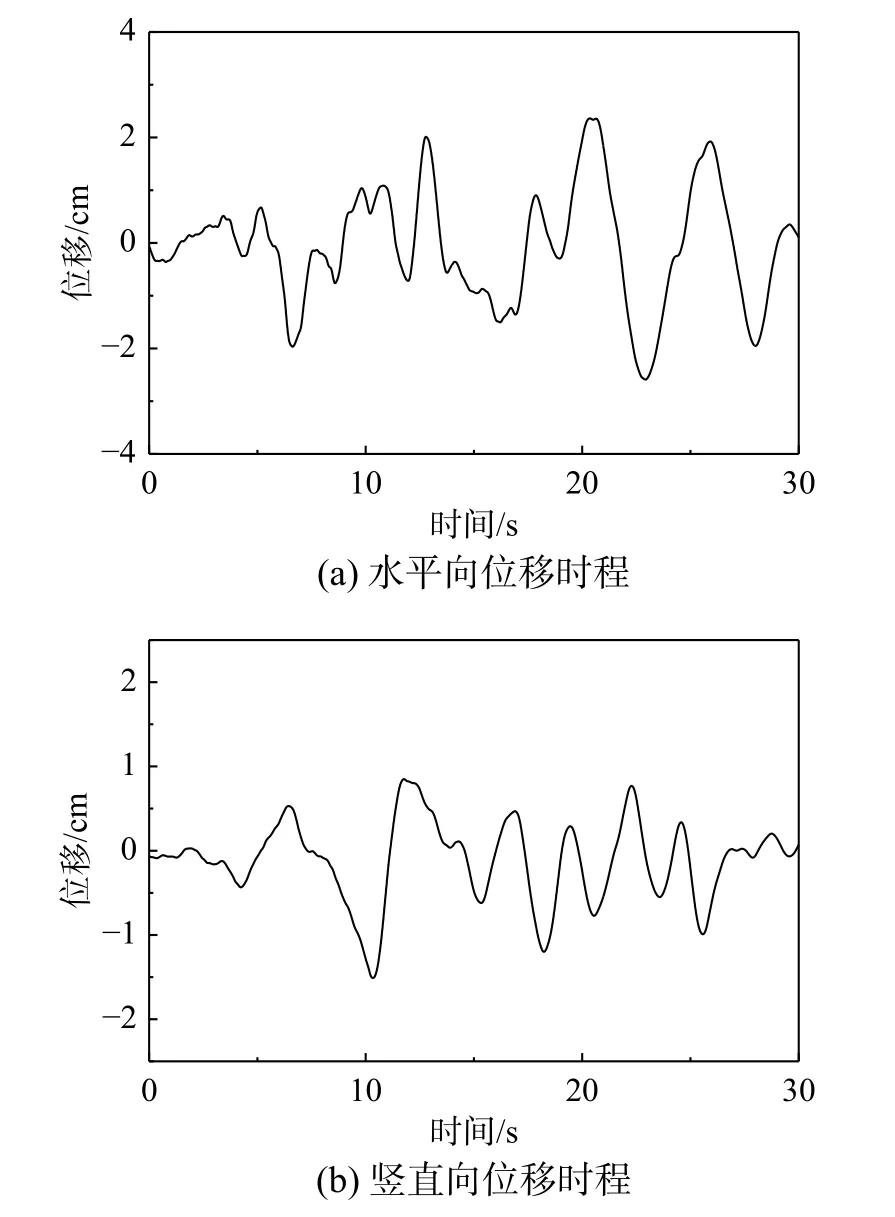
图7 0 m处地震波实测数据Fig. 7 Measured seismic data at 0 m
3.2 覆盖层底部入射的P波、SV波
由入射角和实测地表两向地震动获得入射SV波和P波的位移时程,结果如图8所示。可以看出,SV波与水平向位移时程更为相似,而P波与竖直向位移时程相似,这表明水平向地震动主要由SV波引起,而竖直向地震动主要由P波引起。

图8 入射波位移时程Fig. 8 Time history of incident wave displacement
图9为SV波和P波分别对0 m位置处的水平向位移和竖直向位移的贡献值。根据SV波和P波在两向位移分量上的峰值位移可初步确定SV波和P波对两向位移的贡献百分比。SV波对水平位移的贡献占主要作用,达到75%;P波对竖直位移的贡献占主要作用,其对竖直向位移的贡献达到80%。

图9 SV波和P波对0 m位置处两向位移的贡献Fig. 9 Contribution of SV waves and P waves to two directional displacements at 0 m
3.3 自由场空间特征点地震动
由入射SV波和P波及其入射角建立La Cienega台阵在本次地震事件中的空间自由场,预测各个测点的位移时程及位移傅立叶谱并与实测数据对比。图10~图12分别为0 m、18 m、100 m深度处预测与实测的地震动数据对比情况,由图10~图12可以看出,预测的位移与实测位移幅值基本一致,但在极少时间段下预测与实测位移幅值存在差异。将三个位置处的峰值位移汇总如表1,可见本文预测的峰值位移与实测数据误差不超过10%,结果良好。

图10 0 m处实测地震波与预测地震波数据Fig. 10 Measured seismic wave and predicted seismic wave data at 0 m

图11 18 m处实测地震波与预测地震波数据Fig. 11 Measured seismic wave and predicted seismic wave data at 18 m

图12 100 m处实测地震波与预测地震波数据Fig. 12 Measured seismic wave and predicted seismic wave data at 100 m

表1 峰值位移误差Table 1 Peak displacement errors
对比预测和实测的位移傅里叶谱可以看到,除100 m位置的竖直向傅里叶谱在0.1 Hz~1 Hz误差相对较大,其它位置的预测与实测傅里叶谱基本一致。原因在于选取0 m处的实测地震波作为控制点,而入射波信息是基于控制点的时程确定的,因而距离控制点越深,受覆盖层影响越大,其误差也越大。可见,本文提出的计算方法可以在一定程度上反映地震波在覆盖层场地的传播规律,并保证计算的自由场中控制点的两向时程与设计地震动一致。
3.4 自由场的空间差异性
图13给出了以0 m为中心1000 m范围内两向峰值加速度在不同水平位置的差异性,可以看出,两向峰值加速度沿水平位置存在明显的差异,水平向峰值加速度变化达到10%,竖直向峰值加速度变化达到15%。

图13 两向峰值加速度沿水平位置的差异Fig. 13 Difference of two directional peak accelerations along horizontal position
图14为上述自由场中(0, 0) m、(500, 50) m、(1000, 100) m三个不同空间位置的位移时程。可以看出,无论水平位移还是垂直位移,三点的时间历程都是不同的,不仅存在时滞效应,而且还存在振幅的变化。因此,本文建立的自由场存在明显的空间差异。
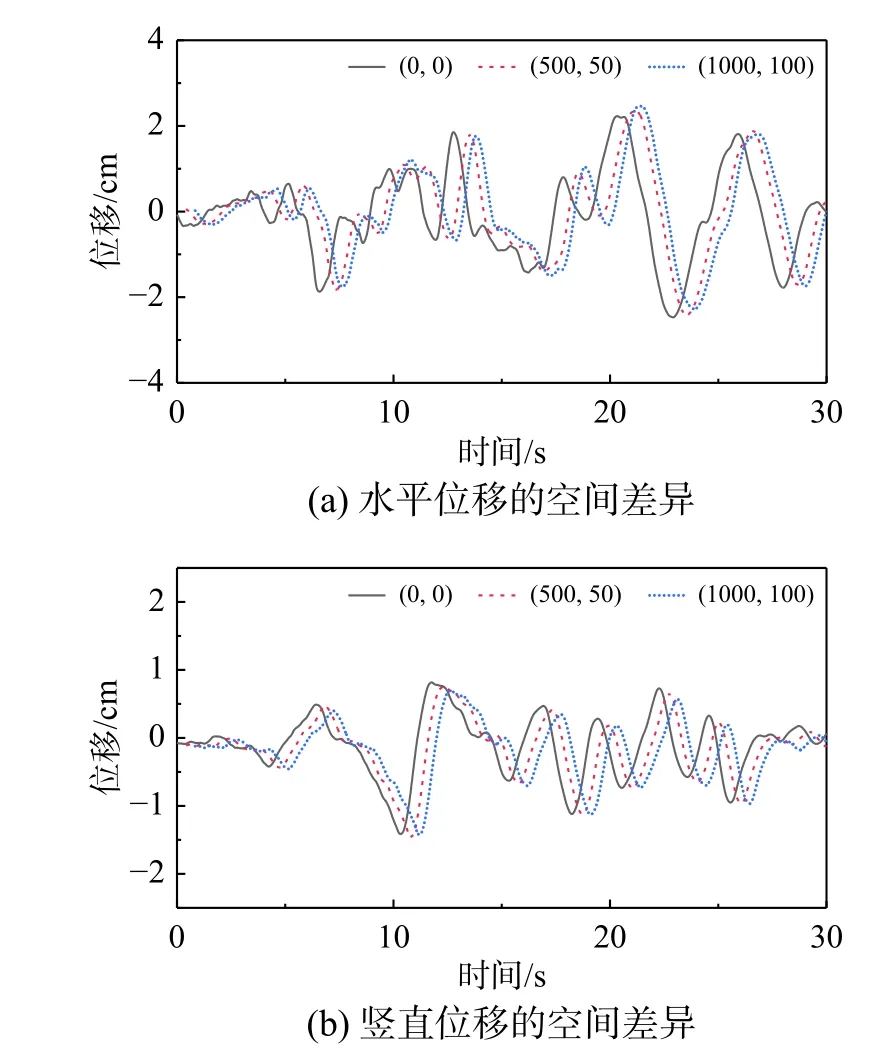
图14 两向位移的空间差异性Fig. 14 Spatial difference in displacement in two directions
4 结论
本文基于覆盖层地表水平和竖直两向设计地震动获得基岩组合入射SV波和P波,实现了基岩-覆盖层场地空间二维自由场构建。
(1)该方法的优点在于SV波和P波信息由控制点的设计地震动反演得到,理论依据充分,同时实现构建的自由场中控制点的时程与设计地震动在水平和竖直方向上一致。
(2)通过La Cienega场地实测台阵记录,验证了本文自由场构建方法的正确性。构建的基岩-覆盖层场地空间自由场任意点水平和竖直两向地震动时程具有空间非一致性,依据入射SV波、P波结合地基人工边界条件以及依据本文方法确定的空间点自由场时程可以实现覆盖层-坝体系统的非一致地震动输入。
(3)需要注意的是,本研究采用的为线弹性模型,引入阻尼比以考虑地震波在覆盖层中的衰减作用,忽略了土体的非线性特性,在中弱地震作用下精度很好,对于强震作用下的自由场构建,误差可能会放大,此时需要考虑土体的非线性。目前,针对考虑土体非线性特性下地震波组合斜入射的有限元模拟问题已展开研究。
