基于COMSOL局域共振声子晶体薄板振动带隙研究

2022-07-04王翌伟徐晓美

噪声与振动控制 2022年3期

王翌伟，徐晓美，林萍

（南京林业大学汽车与交通工程学院，南京 210037）

局域共振声子晶体板是一种周期结构功能材料，具有负等效参数[1]，通过调节单胞结构参数可获得低频段内的禁带[2]。在禁带内弹性波的激励下，声子晶体板的散射体间产生共振，并与弹性波相互作用，从而抑制弹性波的传播。

近些年来，局域共振声子晶体板已成为振动控制领域的研究热点。Oudich等[3]研究了贴附一层或双层柱的板结构的带隙机制，通过调节结构参数，可以改变局域模态与板中Lamb模态之间的耦合方式，从而获得低频带隙。Jin等[4]提出了具有空心柱的声子晶体板，通过调整空心柱内部的直径，能使布拉格带隙和共振带隙相互作用，从而拓宽了带隙。廖涛等[5]将压电材料加入声子晶体板，基于有限元法证明了该结构的可调带隙特性。康太凤等[6]也基于有限元法对所提出的声子晶体板带隙特性及其影响因素进行了研究，证明了所提结构具有优越的低频宽带隙特性，并提出拓宽该结构低频带隙的方法。孙向洋等[7]基于有限元法分析了经典单面柱声子晶体的带隙特性及影响因素，并依此进行了结构优化。Zhu等[8]利用有限元法研究了一种新型二维声子晶体板，该结构能通过调节预应变实现低频带隙的可调谐性。Zhang 等[9]针对车辆噪声、振动与声振粗糙度（Noise、Vibration and Harshness，NVH）问题，提出一种具有填充圆柱体的声子晶体板，并通过色散模拟研究了其带隙特性及影响因素。

鉴于此，本文在验证COMSOL有限元模拟方法用于声子晶体振动带隙计算可靠性的基础上，针对低频振动控制问题，提出一种局域共振声子晶体薄板结构，应用有限元模拟方法研究其带隙结构和元胞结构参数对振动带隙的影响，并考察该声子晶体薄板内部振动波的传输特性，以为类似结构薄板的设计与应用提供理论支撑。

1 弹性波方程及Bloch定理

在线弹性、各向同性、体积无限大的均匀介质中，忽略阻尼的影响，弹性波动方程的矢量形式可写作[10]：

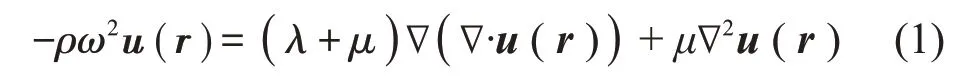
式中：r为位置矢量，▽为哈密顿算子，u为质点位移矢量，ρ为介质的密度，μ和λ为介质材料的拉梅常数，ω为特征圆频率。

由于声子晶体的周期性和对称性，使得晶格中的场也具有一定的对称性。根据Bloch 定理，平移周期性的线性系统的本征场可表示为[11]：

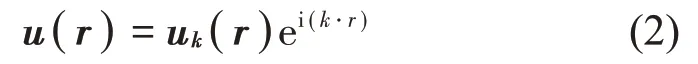
式中：k为Bloch波矢，其幅值函数具有与晶格相同的平移周期性，即：

结合式(3)和Fourier级数数学定理，式(2)表述本征场的波函数可以写为：

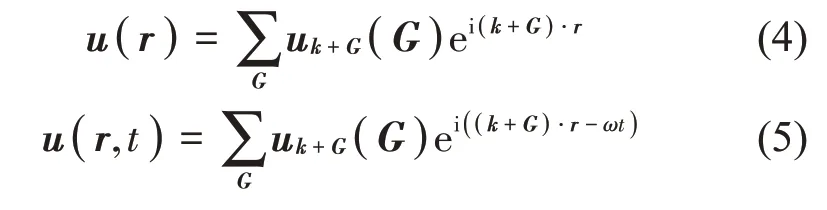
式中：G为倒格矢。由于声子晶体点群的对称性，波矢k的取值范围压缩在第一不可约Brillouin 区内。因此，只需沿着第一不可约Brillouin 区边界上的值遍历一次，就能求得声子晶体的本征频率。

2 带隙计算有限元法

目前，COMSOL等有限元软件具有设置Floquet周期性边界的功能，本节基于弹性波方程和Bloch定理，通过算例阐述应用COMSOL软件计算声子晶体振动带隙的方法，并验证其计算结果的可靠性。

根据Bloch 理论，对弹性波在整个晶格中传播行为的研究可以转换到单个元胞及其第一不可约Brillouin区中进行。元胞的广义本征值方程为[12]：

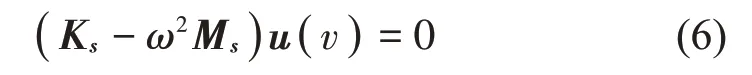
式中：Ks为元胞刚度矩阵，Ms为元胞质量矩阵，u(v)为位移特征向量。

要使元胞中每个点都满足Bloch 定理，只要元胞边界上的所有点满足Bloch 边界条件即可，即要满足式(7)。

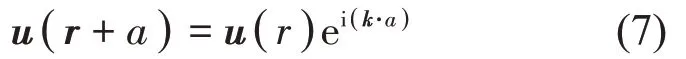
式中：a为晶格常数。

COMSOL 软件中的Floquet 周期性边界设置可约束周期性结构的边界位移，从而实现Bloch 边界条件，其满足的方程为：

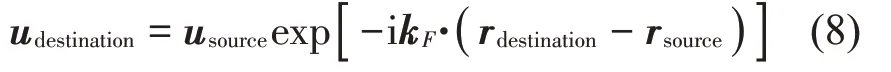
式中：kF为波矢，在软件中通过设置kx、ky和kz表示。usource和udestination分别表示Floquet 周期性边界条件的源端和目标端，rdestination-rsource的结果等于晶格常数。

在COMSOL软件中，对于周期元胞与相邻元胞的非接触面，无须设置边界条件；对于周期元胞与相邻元胞的接触面，则需在元胞边界的对应节点上设置Floquet周期性边界条件。以二维方形元胞为例，其Brillouin 区如图1 所示，阴影部分是第一不可约Brillouin区。首先，取x和y方向的两条边或边界作为两个源项，选择相对的边或边界作为目标项，即在元胞的x方向和y方向各应用一次周期性边界条件。然后，添加波矢k的设置，k∈[0，3]，0到1区间定义为M-Γ边的波数，1到2区间定义为Γ-X边的波数，2到3区间则定义为X-M边的波数。为了与Floquet周期性边界条件中波矢的设置相一致，将k分解为kx和ky表示。接着，对波矢设置参数化扫描，扫描范围0～3，扫描步长0.01，如此波矢能沿着二维元胞的第一不可约Brillouin 区M-Γ-X-M的边界遍历一次。最后，选择相应的特征频率求解器求解，即每给定一个k值，就能根据式(8)，求解式(6)所示的特征值方程。

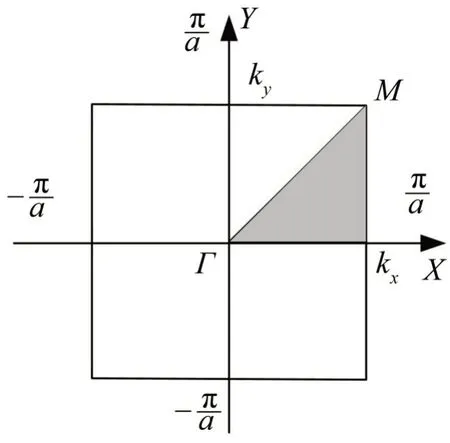
图1 二维方形元胞的Brillouin区

为验证有限元法带隙计算的可靠性，以文献[13]所示的典型单面柱状声子晶体板为例进行带隙计算。图2 给出了该声子晶体板的元胞结构及其Floquet 周期性边界设置，元胞的结构参数为：晶格常数a=10 mm，橡胶板厚度d=2 mm，钢柱半径r=4.8 mm、高度h=10 mm，其色散曲线及带隙如图3所示，图中阴影部分是结构的第一条完全带隙。虽然从图3 可以看出，该算例中的元胞结构具有较宽的低频局域共振带隙，但由于钢柱密度和尺寸比橡胶均质板大得多，工程实际中橡胶板很难提供钢柱所需的支撑强度，故而此结构在工程中很难实现应用。

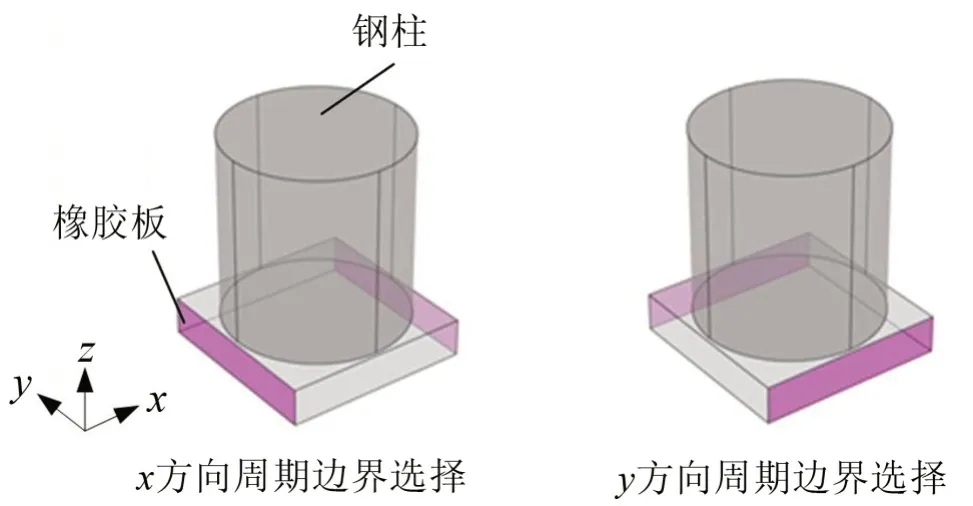
图2 算例元胞结构及其周期性边界设置

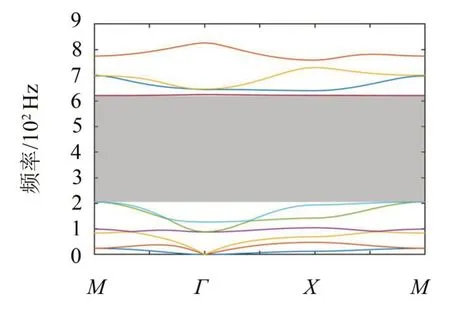
图3 算例的色散曲线及带隙

表1 比较了有限元法和文献[13]的数值方法计算得到的带隙相关结果，从其误差可见，运用有限元法计算带隙是可靠的。

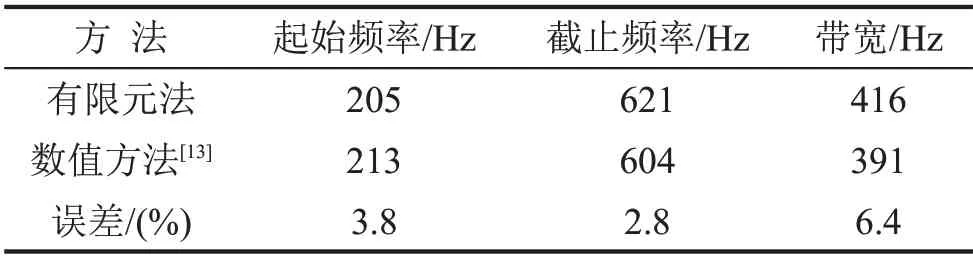
表1 带隙计算结果对比

3 声子晶体薄板带隙特性

3.1 声子晶体薄板结构

本文所研究的局域共振声子晶体薄板结构如图4 所示，图5 是其晶格常数为a的元胞结构，包括三层：上、下层是厚度分别为h1和h2的EVA 板，中间层是厚度为h0的橡胶板；上、下层内嵌的橡胶圆柱半径为r，高度与EVA层厚度相等。元胞初始尺寸参数选为：a=10 mm、h0=h1=h2=1 mm、r=4 mm，材料参数见表2。在该结构中，EVA材料是基体部分，主要起结构支撑作用，橡胶材料充当散射体。由于未贴附金属材料作散射体，所以该结构的总体平均密度较小，并且避免了常规结构中贴附的质量块在振动环境下易掉落的问题，使板的性能更加稳定。此外，该声子晶体薄板结构仅由EVA材料和橡胶材料组成，板的柔韧性与弹性都较好，更易被应用于复杂的振动环境中。

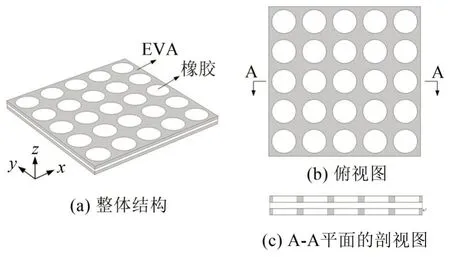
图4 声子晶体薄板结构

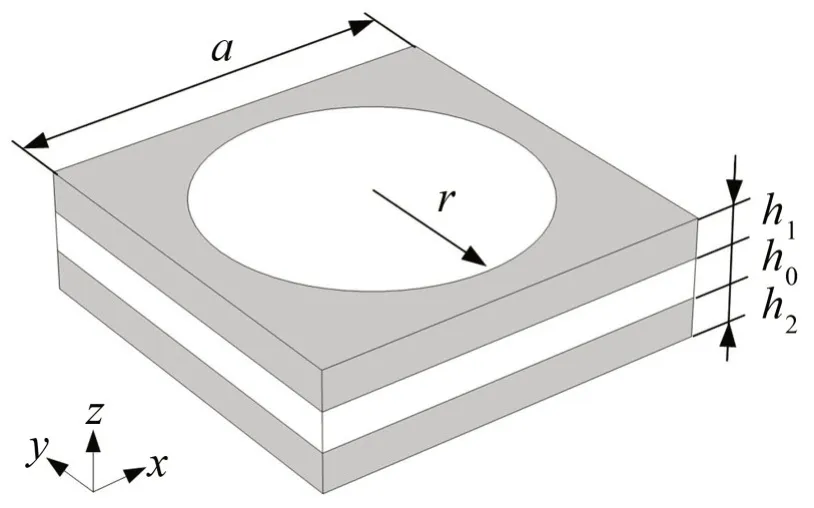
图5 声子晶体薄板元胞结构

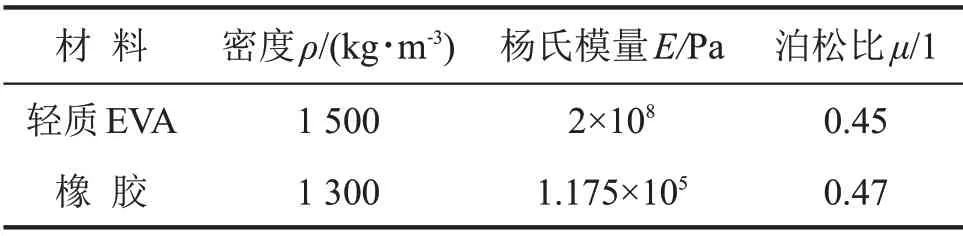
表2 声子晶体薄板材料参数

3.2 带隙特性

建立上述声子晶体薄板元胞的有限元模型，采用有限元法计算其振动带隙，计算结果如图6所示。

根据弹性波传播理论，由图6 可知，板中有Lamb 波和水平剪切波，其中，Lamb 波分为反对称Lamb波（弯曲波）和对称Lamb波。图6中有三条能带从G点出发，沿三个方向分开，其中，两条能带在G点附近呈线性上升，分别对应着板中的水平剪切波和对称Lamb波，由于在低频范围内这两种波的传播特性与在均匀介质中传播特性相近，因此总体表现为线性。第一条能带对应着板中的弯曲波，从图6可以看到，在第一条能带和第二条能带间没有任何弯曲波穿过，形成了一条完全带隙，即弯曲波带隙，带宽为88 Hz，带宽频率范围为448 Hz～536 Hz。

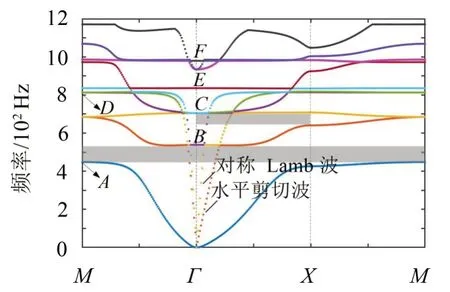
图6 振动带隙结构图

为进一步说明板的振动带隙形成机理，图7 给出了图6 中几个关键点的振动模态图，图中用散布在结构中的箭头表示区域位移的相对大小和方向。第一条能带是形成弯曲波带隙起始频率的关键，从图7 中A 点的振动模态可以看出，元胞中间的橡胶圆柱以及与橡胶圆柱相连的橡胶薄板均向z轴正方向运动，而EVA板基本不动，即振动集中在中间，此时A 点对应于结构发生了局域共振，使得弯曲波与之发生强烈耦合，致使弯曲波的能量局限在橡胶材料中而不能继续传播，从而使第一条能带被截断，继而开始出现带隙。带隙在B点所对应的平直带处截止，观察B点的振动模态可知，橡胶圆柱和橡胶板依旧向z轴正方向运动，而EVA 基体板开始向与橡胶部分相反的方向运动，该运动模式标志着局域共振的消失，此后，弯曲波便能够在元胞内通过。

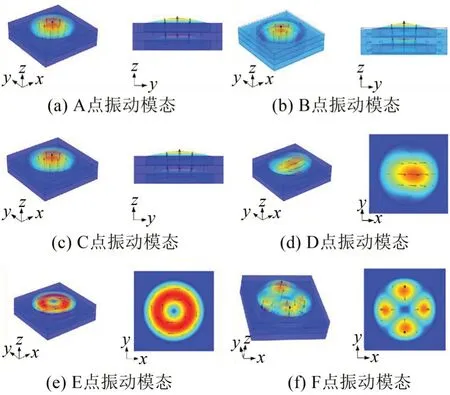
图7 A～F点的振动模态

从图7还可以看出，在带隙上方的频段内，能带图中还存有一些近似水平的平直带，观察相应C、D、E、F 点的振动模态，同样发现振动位移基本都在橡胶圆柱和橡胶板内，同时EVA 基体基本不动，可见相应的结构均发生了局域共振。虽然这些局域共振模式不能像A 模式一样形成完全带隙，但是它们的存在有利于方向带隙的产生，如在图6 的C 点附近有一条Γ-X方向的弯曲波带隙（图中阴影）。

3.3 带隙特性影响分析

为探究元胞弯曲波带隙的调控规律，指导带隙特性优化，分析了结构参数（包括圆柱半径r，中间橡胶层厚度h0，上、下EVA层厚度h1、h2，晶格常数a）对振动带隙的影响规律。图8至图12的左侧纵坐标对应带隙的起始频率和截止频率，右侧纵坐标对应带隙宽度。

图8 圆柱半径r对振动带隙的影响

图8 为元胞中橡胶圆柱半径对振动带隙的影响。由图可知，随着圆柱半径r的增大，带隙的起始频率和截止频率都向低频区域大幅度移动，当半径r从2 mm 增至4.5 mm，起始频率下降了近60 %；同时，带隙的宽度从63 Hz拓宽到92 Hz。

图9 为元胞中间橡胶层厚度对振动带隙的影响。由图可见，随着橡胶层厚度增加，带隙的起始频率和截止频率都向高频区域移动，带隙先变宽再变窄。

图9 中间层厚度h0对振动带隙的影响

图10为元胞的上、下层EVA板厚度对振动带隙的影响。由图可见，随着上、下层厚度增加，振动带隙的起止频率和截止频率都向高频区域移动，且带隙随之变宽。

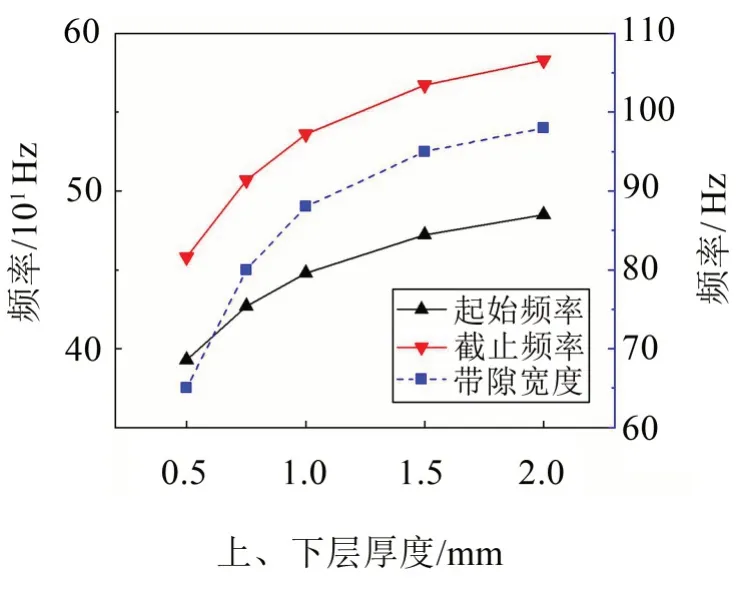
图10 上、下层厚度h1、h2对振动带隙的影响(h1=h2)

由于晶格常数a受限于圆柱半径r，因此其对振动带隙的影响可分两种情况讨论。

一种是圆柱半径r不变，即仍为4 mm，考察振动带隙随晶格常数a的变化规律，如图11 所示。从图中可以看出，随着晶格常数增大，带隙起始频率略有下降，截止频率也随之下降，同时带隙宽度逐渐变小。

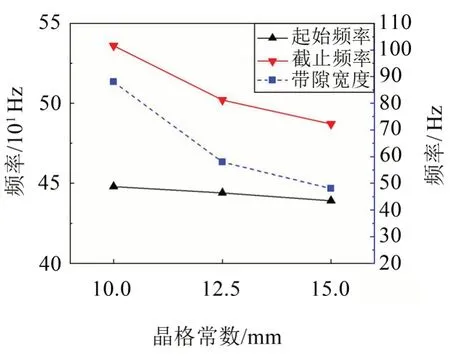
图11 晶格常数a对振动带隙的影响(r=4 mm)

另一种是圆柱半径与晶格常数的比值r/a不变，即r/a=2/5，考察晶格常数a对振动带隙的影响。通过对不同晶格常数a开展多组仿真试验，得到能较好反映晶格常数对振动带隙影响规律的对比数据，如图12 所示，图中晶格常数的变化间隔为5 mm。由图可以看出，随着晶格常数增大，带隙的起始频率和截止频率都明显向低频区域移动，带宽也随之迅速减小。因此，总体来说，大的晶格常数会产生更低频段和更窄的振动带隙。

图12 晶格常数a对振动带隙的影响(r/a=2/5)

总之，对于此声子晶体薄板，要使振动带隙产生于低频区域，可以增加圆柱半径或增大晶格常数，但增大晶格常数会使带隙宽度变窄。增加薄板中间层厚度或上、下层厚度都会使带隙往高频区域移动。因此，为使声子晶体薄板能在低频区域产生较宽的振动带隙，对上述结构参数进行了优化组合研究，其中晶格常数a的3个参考值分别为10 mm、15 mm和20 mm，相应的圆柱半径r的参考值分别为4 mm、6 mm和8 mm，以维持r/a的比值为定比2/5；上、中、下三层薄板的厚度参考值分别为0.5 mm、1 mm 和1.5 mm，且使上、下层板的厚度相等，即h1=h2。

基于上述结构参数，对枚举法所得的27组参数组合方案开展了0到1 000 Hz范围内的振动带隙仿真研究。以汽车上200 Hz～400 Hz 的中、低频为目标频段，选择带隙宽度在目标频段内占比最大的参数组合为最优方案。由仿真结果可知，当晶格常数为15 mm、圆柱半径为6 mm、三层薄板厚度均为1.5 mm 时，所得局域共振声子晶体薄板的振动带隙在目标频段内的占比最大（29%）。此时，振动带隙的起始频率为299 Hz、截止频率为357 Hz。图13即是通过枚举优选出的声子晶体薄板的振动带隙结构图。可见，通过结构参数调整，已使声子晶体薄板的振动带隙移至低频段，但带隙宽度有所减小。

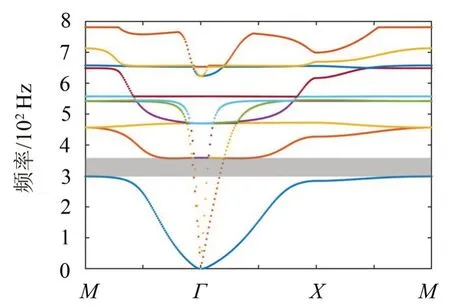
图13 优化后元胞的带隙结构图

4 振动传输损失

为考察振动带隙内声子晶体薄板对波传播的阻碍作用，讨论了频域上波的传播特性。基于COMSOL软件固体力学模块的频域研究，建立了有限周期结构在频域上的传输特性分析模型，如图14所示。图中，x方向和y方向均有20 个元胞，元胞的结构参数为优选后的尺寸，所构成的有限周期结构尺寸为300 mm×300 mm×4.5 mm。

如图14所示，在薄板的左侧边界施加垂直于板面的位移激励w0，在另一侧边界拾取位移响应w1，利用积分算子计算左右侧z方向上的位移幅值，并用传输损失表征波的衰减，传输损失（Transmission loss，TL）计算式为[14]：

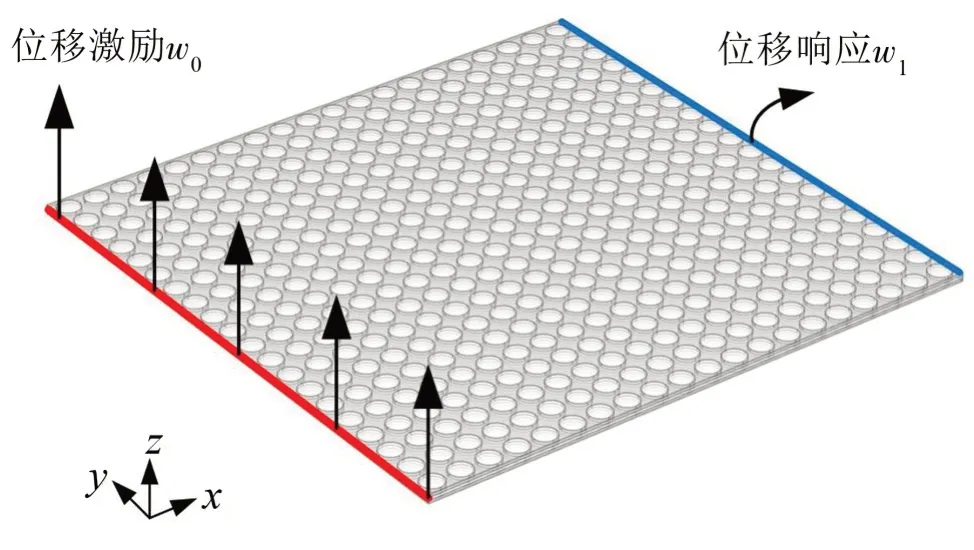
图14 有限周期薄板的载荷示意图

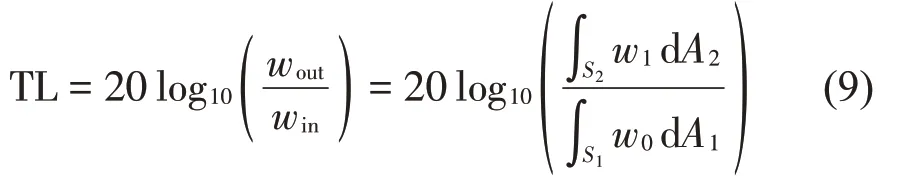
式中：win和wout分别为激励边界和响应边界z方向上的位移幅值，A1和A2为对应的边界面积。

仿真计算的频率范围设定为10 Hz～1 000 Hz，计算间隔为10 Hz，计算得到的声子晶体薄板在频域上的传输特性如图15所示。

从图15可以看出，在300 Hz～350 Hz频率范围内，传输损失明显增大，最大衰减量为71.6 dB，出现在频率为310 Hz 处，衰减频率范围与图13 所示的299 Hz～357 Hz振动带隙基本吻合。

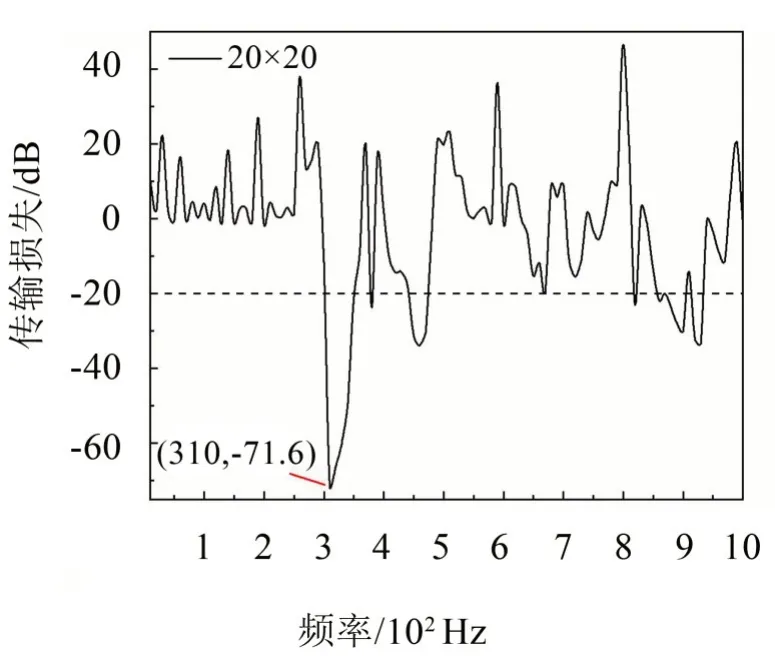
图15 声子晶体薄板在频域上的传输特性

为进一步呈现振动带隙内板对波传播的阻碍作用，图16给出了带隙内频率为310 Hz和带隙外频率为500 Hz时声子晶体薄板z方向的振动位移。

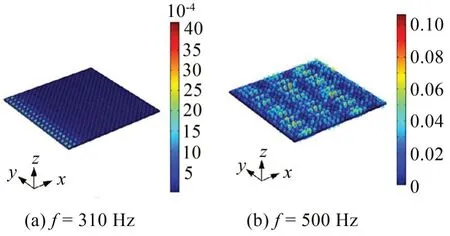
图16 声子晶体薄板的振动位移图

由图16可以看出，对于振动带隙内的310 Hz频率，板左侧的位移激励产生的弯曲波被局限在左侧的呈局域共振模式的元胞中，板右侧的z向振动位移几乎为0；对于振动带隙外的500 Hz频率，声子晶体薄板呈现出明显波动，即弯曲波能通过薄板传播从板的左侧到达板的右侧。可见，在振动带隙内，声子晶体薄板能很好地控制板内的弯曲波在相应频段内的传播，从而控制薄板的振动。