集约型时间触发以太网拓扑优化方法

汪 清，伍晨邦，陈 鹏，周 虎，吴芝亮

集约型时间触发以太网拓扑优化方法

汪 清1，伍晨邦2，陈 鹏1，周 虎3，吴芝亮4

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津大学国际工程师学院，天津 300072；3. 北京航天自动控制研究所，北京 100070；4. 天津大学机械工程学院，天津 300072)

时间触发以太网(time-triggered ethernet，TTE)是一种时间业务与事件业务混合技术，其在兼容标准以太网基础上，保障时间触发(time-triggered，TT)业务的确定性和可靠性，在航天通信领域具有显著的优势．但由于航天网络的高成本问题，在很大程度上限制了TTE的发展，因此研究集约型网络拓扑可降低系统架构成本．本文首先引入复杂网络理论，在满足速率约束(rate-constrained，RC)消息延迟界门限的前提下，建立简化网络拓扑结构的问题模型．其次提出最小介数节点删除及混合策略恢复的集约型拓扑优化算法，通过对节点和边的交替迭代收敛到目标函数最小化的状态．最后，在优化后的集约型网络基础上设计双冗余结构，提高时间触发业务的可靠性．实例的优化前后结果表明，不同恢复策略在不同网络结构下性能不同，说明所提出混合策略的优势．通过优化目标函数对比表明所提出的方法能兼顾时延的前提下简化网络拓扑结构，降低架构成本．本研究给出了基于TTE的实时航天通信的设备部署优化算法及恢复策略，可用于旧网络的升级与改造．通过实例给出了在随机的BA无标度网络中，实现模型建立和拓扑优化的过程，其算法思路和设计方法可进一步应用于更大规模的网络拓扑优化，为航天通信网络优化提供了参考．

时间触发以太网；拓扑优化；架构成本；网络时延；双冗余设计

对于分布式航空电子系统而言，其系统实现的关键在于节点间通信的实时性和确定性．时间触发以太网(time-triggered ethernet，TTE)将时间触发技术的实时性、确定性、容错性同普通以太网的灵活性、动态性和“尽力传”相结合，为同步的、高度可靠嵌入式计算与网络、容错设计提供支持，在航天航空领域得到了广泛的应用[1-2]．

航天总线的设计和部署需要面对机载内部可利用空间狭小、架构复杂且成本高昂的问题，研究拓扑优化算法具有重要的实用价值．

拓扑优化是在某些约束下为了满足某些目标对结构设计的优化．多数情况下需要对冲突的多子目标求取Pareto最优解[3]．Beshley等[4]证明了固定网络拓扑下可以通过路由管理提高网络性能．Lee等[5]提出了通过资源偏好感知路由算法平衡网络使用资源，提高了路由请求的性能瓶颈．Noman等[6]设计了线性控制器根据负载分配来缓解网络拥塞问题，Zhang等[7]研究了基于相对延迟和实时约束的设备分配问题，同时，提出了一种基于模拟退火的优化方法和双冗余拓扑结构．王红春[8]设计了考虑负载均衡和架构成本的目标函数来优化拓扑．Abdel等[9]提出了一种处理多目标优化问题的均衡优化算法(MEOA)求取折衷的解．

本文针对航天总线系统集约化设计的需求，优化TTE网络拓扑，在保证延迟性能的前提下最小化架构成本．首先，为研究网络性能，引入复杂网络量化性能表现，复杂网络包含4种拓扑结构调整方式：删除节点或边[10]、新增节点或边[11]、重连边[12]和边有向化[13]．接着，采用网络演算方法分析速率约束(rate-constrained，RC)消息的延迟上界[14-16]．分析延迟上界是为了确保节点通信的确定性．然后，提出删除节点或边和新增边的方式优化拓扑，在保证时间触发(time-triggered，TT)消息实时性、确定性前提下，考虑介数最小节点删除和混合拓扑恢复策略，使得优化后的拓扑结构能够满足网络延迟的要求，提高RC消息的确定性．最后在上述基础上设计成双冗余拓扑结构提高TT消息的可靠性．

1 集约型拓扑优化系统模型与问题描述

为了建立网络拓扑优化问题模型，首先将实际拓扑抽象为图的形式，方便计算网络参数，如节点介数、边介数等．将交换机和终端作为节点，双向物理链路作为无向边．时间触发网络的实际拓扑如图1(a)所示，物理链路采用全双工传输，图中带箭头的实线表示业务传输的逻辑方向．抽象后的拓扑结构如图1(b)所示．

图1 拓扑结构到网络模型的抽象

1.1 基于网络演算的延迟界

虽然时间调度表可以保证TT消息的时间确定性，但是由于RC消息需要经过多级复用排队，因此RC消息时延的确定性界限变得复杂且无法保证．但是航天系统又必须保证所有的消息延迟在可控范围内，这样才能确保整个通信系统的确定性[17]．因此时对于实时网络而言，通信消息的端到端延迟的可预测性或延迟上界比统计特性更重要[18]．此外，由于BE 消息的优先级低于RC消息，因此用RC消息的延迟状况表示网络延迟，可反应网络通信状况．

网络演算方法指的是以最小加代数和最大加代数为基础，分析网络性能的最坏边界．在确定的网络拓扑和业务模型下，可用网络演算方法[19]分析流量在最坏情况下的端到端延迟作为网络的性能指标．按照最坏情况下的端到端进行延迟计算，RC流量在网络中的延迟上界是其所有访问过的节点上可能的最大延迟和抖动之和．

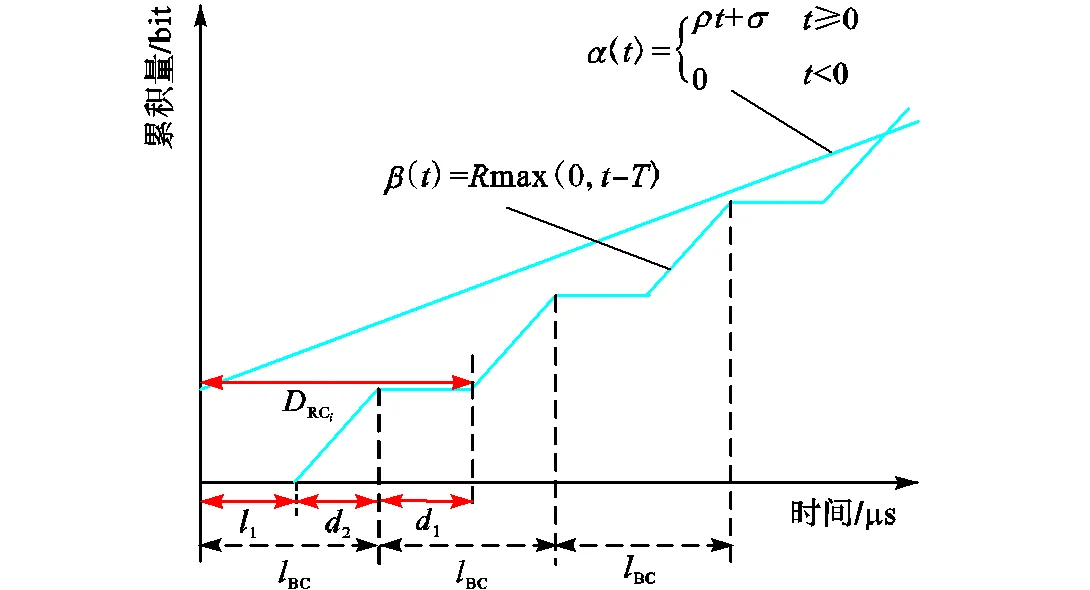
图2 到达曲线与服务曲线的最大水平距离计算

假设在网络拓扑中源端发送条RC消息，目的端不定，且源端受到最大帧长与最小帧间隔的限制，即源端的个RC消息的最坏延迟[21]为

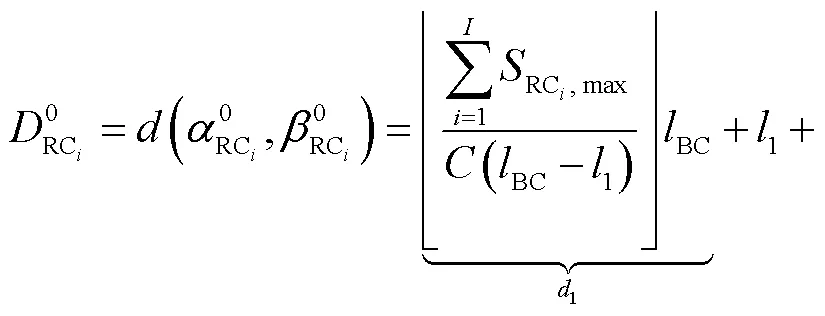
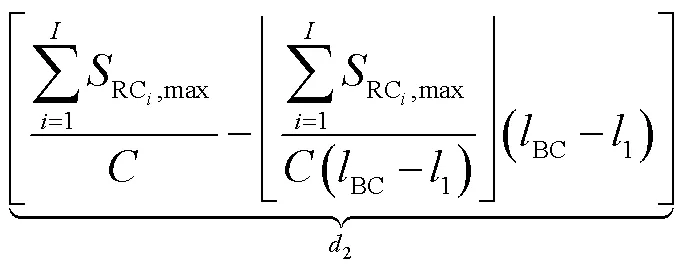
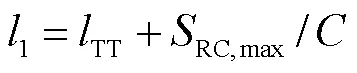
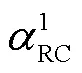
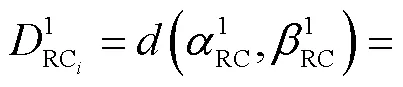
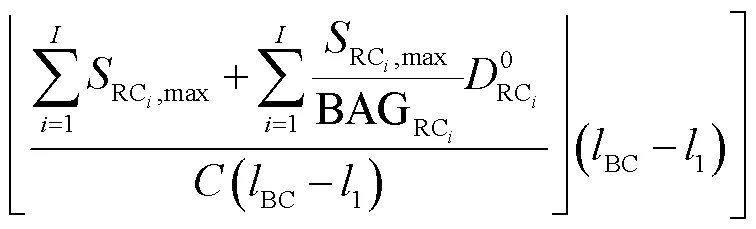
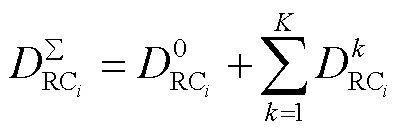
1.2 架构成本

成本对于网络的广泛应用一直是一个重要的限制因素，降低成本是网络部署的重要目标之一．对于一个给定的网络拓扑，不考虑通信开销和架构维护开销，成本主要由终端、交换机、链路三者的成本组成．在拓扑优化过程中，终端是固定的，因此主要对交换机和链路的架构成本进行优化．

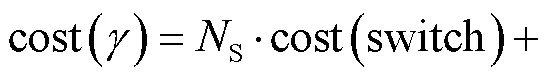
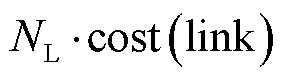
1.3 目标函数

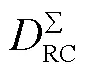
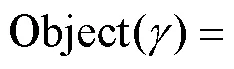
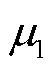
2 最小介数节点删除及混合策略恢复

网络拓扑的优化问题，本质上是基于消息流和网络组件特性所设计的一种多目标优化问题．网络拓扑优化问题不同于路由选择问题，路由算法是在拓扑已知的前提条件下，按照业务需要选择合适的路由路径．本文重点研究的是TTE网络的拓扑优化问题，具体来说，是在给定TT流量任务的情况下，考虑RC流最大延迟和网络的成本，通过调整交换机与链路，设计集约化的网络拓扑．所提出的TTE拓扑优化算法如图3所示．由于TT流是事先规划的，已经离线设计好了调度表，在优化过程中不删减TT流量涉及到的交换机和链路，无需改变调度表，仅对RC流量涉及到的路由和拓扑进行调整．首先，根据给定的TT业务和RC业务设计能实现所有业务路由功能的任意拓扑及其路由方式，得到初始拓扑和初始路由表．然后，设计综合考虑架构成本和延迟性能的目标函数(6)，将目标函数作为拓扑的量化评价标准，筛选出网络延迟尽可能低，架构尽可能更简单的拓扑方案．优化过程分为目标交换机删除及拓扑恢复、混合策略择优及链路去冗余3部分．最后，为了保证TT消息的可靠性，在优化后拓扑的基础上进行TT的双冗余备份(见第3节)，得到最终拓扑方案．

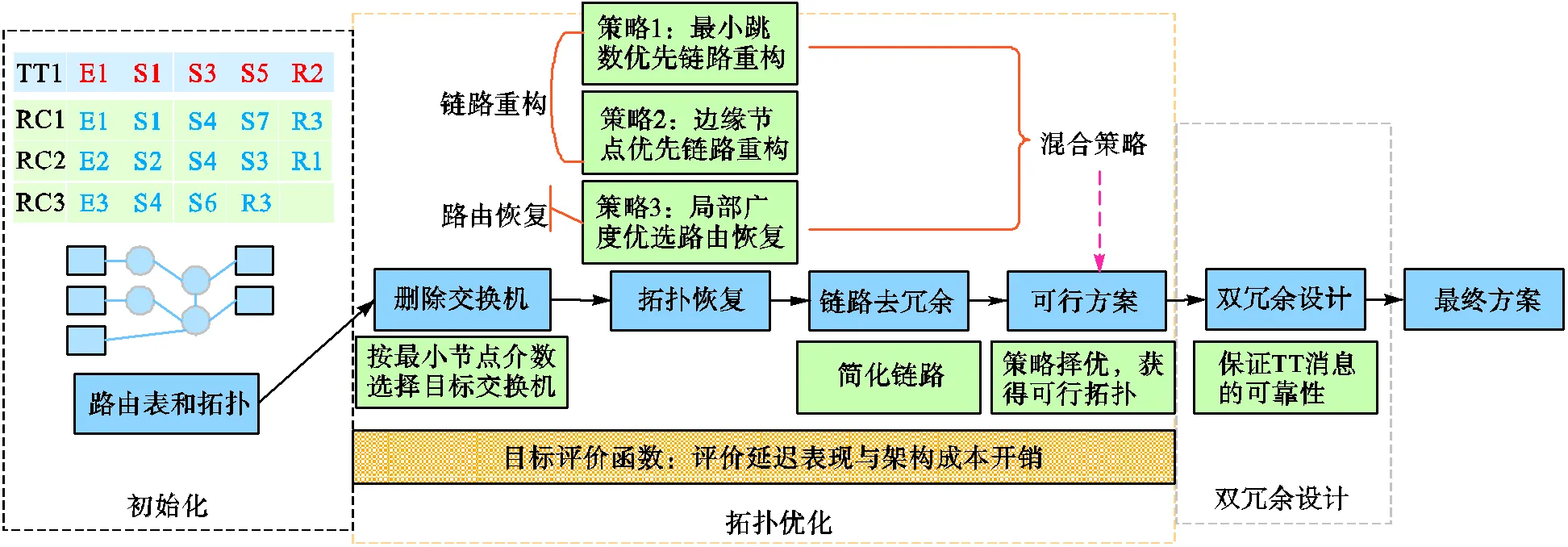
图3 TTE拓扑优化流程

2.1 目标交换机删除及拓扑恢复

由于交换机的成本和重要性高于物理链路，因此在获得初始拓扑和路由表后，优先优化交换机，目标是尽可能减少交换机数量．交换机优化流程如下．

首先，识别是主动优化还是被动优化．主动优化对交换机按照重要性进行排序，然后从低到高选择目标，节点交换机的重要性根据其节点的介数值衡量，即通过该节点的路由路径的数量越多，该节点交换机越重要．被动优化随机选择一个交换机作为目标交换机．

其次，选中目标交换机后进行删除和拓扑恢复．删除之前需要先判断目标交换机是否是TT流量经过的交换机．如果删减会影响到TT任务的传输调度，则不能删除，此时如果还存在其他可优化的交换机，选择下一个目标交换机开始交换机的优化删减，如果不存在其他可优化的交换机，则交换机优化终止．如果目标交换机不承载TT流量，则可对其进行删减．随后调用3种恢复策略进行拓扑恢复，其中恢复策略1和恢复策略2是添加物理链路进行链路重构，恢复策略3是直接进行路由调整，但可能无法满足RC任务的需求．

1) 恢复策略1

从删除的目标节点出发，将目标交换机的前后节点直接连接．前后节点优先选择最小跳数按照初始路径进行链路重构．

2) 恢复策略2

从删除的目标节点出发，选择目标节点前后的边缘节点进行连接．边缘性的强度通过节点介数值衡量，节点介数的值越低，交换机的边缘性越高．由于边缘性强的节点上通过的路由路径数量更少，发生拥塞的概率更低，因此对筛选出被删除的目标节点前后节点中边缘性最强的两个节点进行连接，其他节点与这两个边缘性最强的节点连接，实现间接连接．

3) 恢复策略3

最简单的是直接进行路由调整，重新对删除目标节点后的网络进行路由．路由恢复采取局部广度优先遍历的方法．若重新规划的路由表能够满足RC任务的需要，那么无需添加链路即可得到可行拓扑．但重新规划的路由可能无法满足RC任务的需求，例如无法建立RC任务的源-目逻辑链路，则只能采用恢复策略1或恢复策略2进行链路重构，获取可行拓扑结构．

完成拓扑恢复后，计算可行拓扑的目标函数值．如果目标函数值小于初始拓扑或优于上一轮结果，则用当前优化结果更新拓扑和路由．若仍有目标交换机可以优化，则进入下一轮目标交换机的删除和拓扑恢复过程．如果目标函数值均大于初始拓扑和上一轮结果，则此轮不能优化，选择上一轮的结果并结束优化过程．

以下通过实例介绍交换机删除及拓扑恢复的实现过程，给定如图4所示的初始拓扑和路由，记为示例1．考虑主动优化的情况，根据路由表，按照节点介数计算各交换机的重要性，如TT1经过交换机1和交换机3，交换机1和3分别“加1”，得到各交换机上的节点介数从低到高排序为{S1：3，S5：4，S7：5，S3：5，S2：6，S4：8}．对交换机按照重要性从低到高进行优化删减，第一个待删除的目标交换机为S1．按照S1、S5、S7、S3、S2、S4的顺序优化删减．

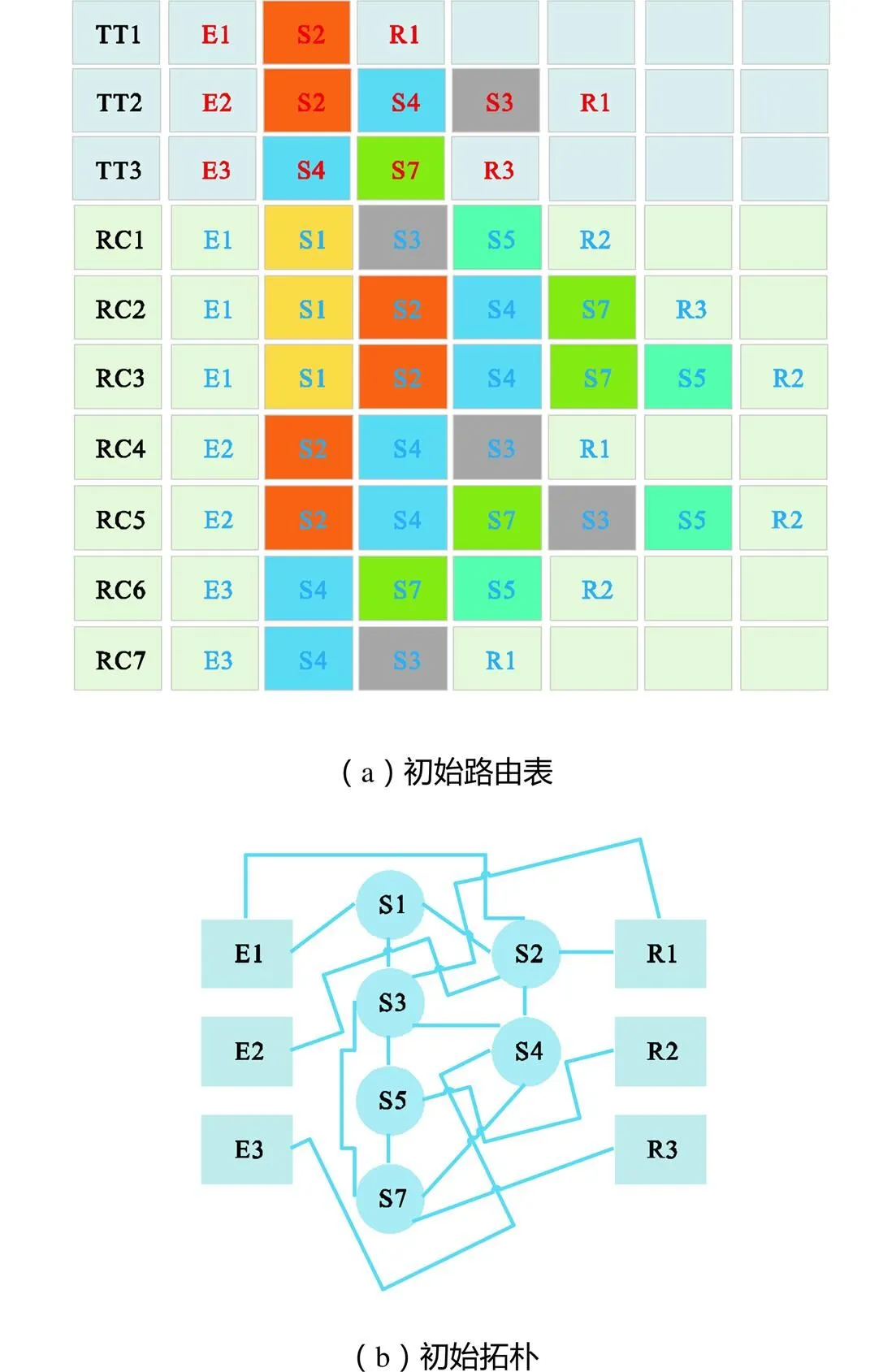
图4 初始路由表和拓扑示例1

删减S1后，初始拓扑中的交换机S1及与S1相连的链路都会删除．交换机删除与拓扑恢复示例1如图5所示．如图5(a)所示，黄色虚线部分为删减的交换机和物理链路，此时路由RC1、RC2和RC3将受到影响．

图5(b)所示为按恢复策略1(最小跳数优先链路重构)得到的拓扑．交换机S1的邻居节点包括S2、S3和E1，目标交换机前端路径为E1→S1，后端路径为S1→S2和S1→S3，删减交换机S1后，策略1选择最小跳数的方式直接按照初始路径进行链路重构并连接目标交换机的前后节点．E1位于前端，S2和S3位于后端，重构的链路为E1→S2和E1→S3，如图中橙色部分所示．

图5(c)所示为按恢复策略2(边缘节点优先链路重构)得到的拓扑．选择边缘节点进行链路重构，边缘性大小与节点介数大小成反比．目标节点后端的节点S2与S3的介数分别是6和5，S3更边缘，因此目标节点后端选择S3，目标节点前端仅有E1一个节点，且为发送端节点，因此直接选择E1作为前端的边缘节点．链路重构策略为E1→S3、S3→S2、E1通过S3到达S2，如图中橙色部分所示．

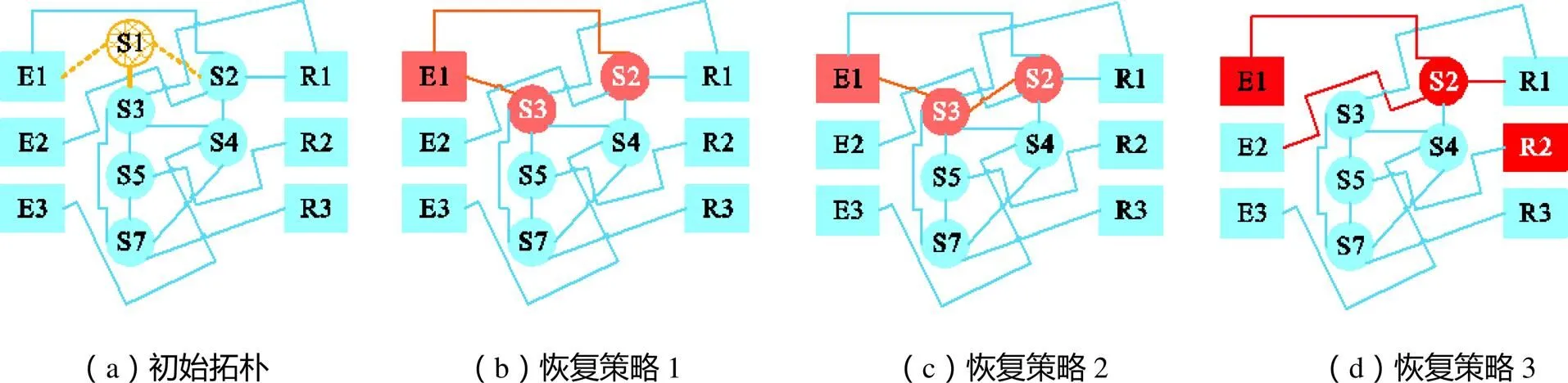
图5 交换机删除与拓扑恢复示例1

图5(d)所示为按恢复策略3(局部广度优先路由恢复)得到的拓扑．依次判断受影响的RC任务是否能够找到路径进行传输，如对于RC1而言，如图中红色部分所示，发送端为E1，接收端为R2，E1的邻居节点仅S2，S2的邻居节点只有E2、E1、R1．在S1交换机被删除后，找不到任何一条路径使得路由RC1能够从E1出发，最终到达R2，因此在图5(d)所示的拓扑结构上进行路由调整，无法满足RC任务的需求，该策略不可行．

如图6和图7(a)所示给定初始路由表和初始拓扑，记为示例2．图7(a)中的绿色部分的交换机和链路是被删除的部分．通过3种恢复策略得到7(b)，7(c)和7(d)．与示例1相同，策略1选择最小跳数按照初始路径添加物理链路得到，策略2通过寻找“边缘节点”添加物理链路得到．与示例1不同，示例2通过策略3可以找到路由满足RC任务的路由调整方案，如图中绿色部分所示．删除交换机S2后，受影响的RC路由包括RC4与RC5，RC4从E2→S2→S5→R1调整为E2→S3→S5→R1，RC从E2→S2→S3→S4→S5→S7→R2调整为E2→S3→S4→S5→S7→R2，此时策略3可行．

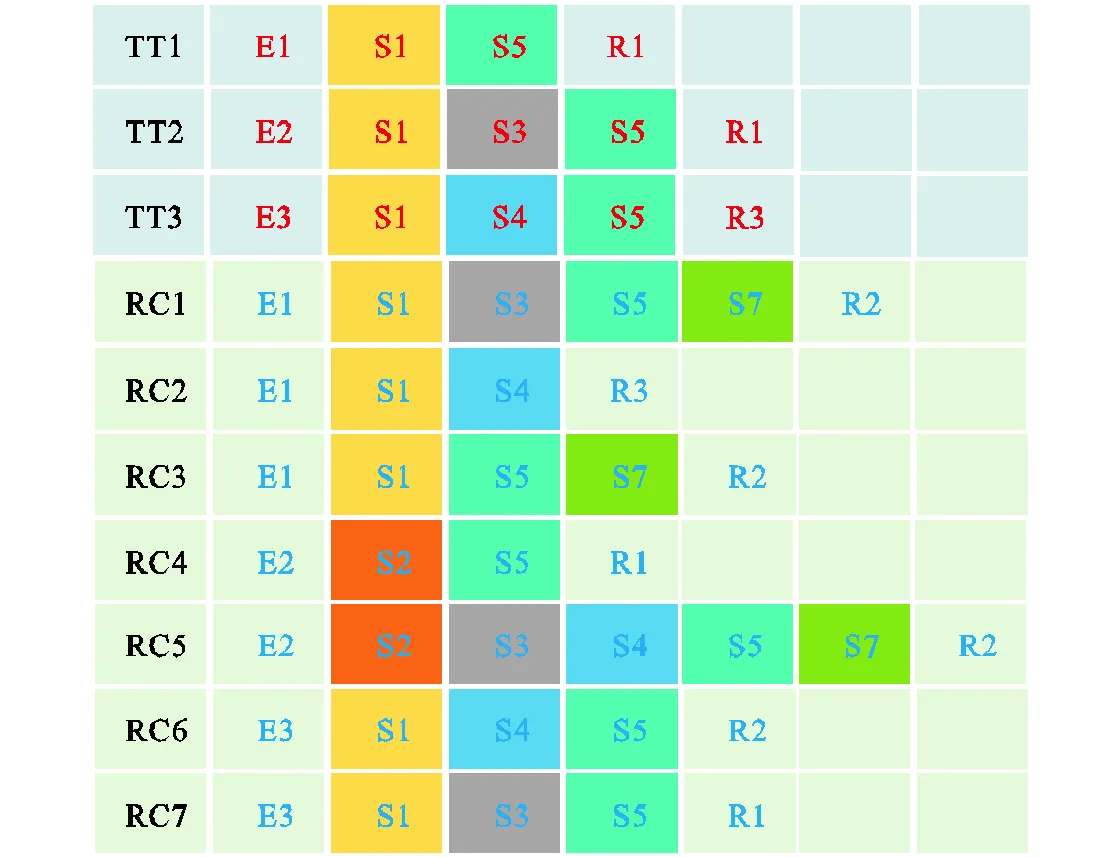
图6 示例2的初始路由

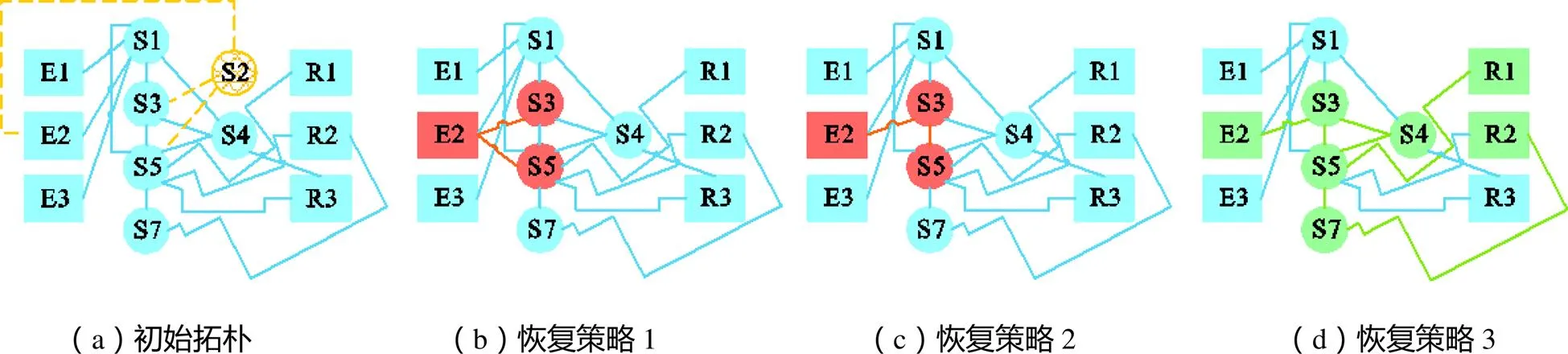
图7 交换机删除与拓扑恢复示例2

2.2 混合策略择优

混合策略择优指交换机删减后通过3种恢复策略进行拓扑恢复，并对目标函数进行评价和择优．第1.3节设计的目标函数综合考虑架构成本和延迟性能，通过计算策略恢复后可行拓扑结构的目标函数，量化各个拓扑结构在网络延迟和架构成本上的表现，在可行拓扑方案中选择目标函数值最小的拓扑结构.

如果最小的目标函数值小于初始拓扑的目标函数值，则将这个拓扑结构作为交换机删除和恢复后的拓扑．由于目标函数中对超过RC延迟的情况加了惩罚项，一旦出现RC延迟无法满足需求的情况，目标函数值会远大于满足网络情况．考虑到每一轮优化都是贪婪的，因此将停止迭代的条件设为目标函数值大于初始拓扑的目标函数值或目标函数值不再较上一轮减少，此时表明目标交换机不能再删减，拓扑方案应取上一轮优化后得到的结果．经过尽可能多轮的交换机删除和拓扑恢复后，构建出满足延迟约束的集约化拓扑结构．

2.3 链路去冗余

由于在交换机删除与拓扑恢复过程中引入了添加链路的重构策略(恢复策略1和恢复策略2)，可能会导致链路存在冗余，需要在后续执行链路去冗余．

由于TT任务传输的实时性和确定性需求，在链路的去冗余操作时，不优化影响到TT任务的物理 链路．

链路去冗余流程过程如下．首先，按照链路重要性进行排序，重要性通过边介数衡量，即每条物理链路上经过的路由的数量．然后，按照链路的重要性从低到高选择目标链路，进行去冗余删除．

如果在某条目标链路删除后，路由调整无法完成所有的RC任务(路由不通)，则重新选择下一条目标链路．

删除目标链路之后，先进行路由调整完成拓扑恢复，若能调整成功，则计算调整后的目标函数值，小于初始拓扑或优于上一轮结果，更新链路删除后的拓扑和路由，进入下一条目标链路的去冗余优化．

如果在某条目标链路删除后，目标函数值大于初始拓扑(RC延迟界超过门限)，则停止优化，上一轮的结果即为链路优化的结果．

仍以图4所给出的示例1为例，进行链路优化．交换机优化过程中删减了S1与S5，当继续删减S7后，拓扑恢复后的目标函数值会大于初始拓扑，因此交换机优化的结果是删除S1与S5，如图8(a)所示，图中黄线部分为按最优恢复策略(恢复策略1)所添加的链路．接下来进行的链路优化，图中绿线虚线S7→S3为重要性最低的链路，是最先被删除的链路．图中红色实线S4→S3为重要性次低的链路，但是在删减这条链路后，计算得到的目标函数超过了上一轮，因此不能删除该链路，最终优化后的结果删除了绿线虚线S7→S3，结果如图8(b)所示．

图8 示例1 的链路去冗余

3 双冗余设计

通过TTE协议调度表有效保证了TT消息传输的实时性和确定性．但是，除高实时性及高确定性外，TT消息传输还需要高可靠性．因此，本文还设计了双冗余以保证TT消息的可靠传输．

双冗余方案如图9所示，节点和节点上有需要周期发送的TT消息．发送端在设计报文格式时，在以太网报文的数据区中加入报文的时间标签，然后分别通过初始通道和备用通道传输．对TT消息的物理通道采用双冗余备份传输，在初始通道和备用通道上发送相同的TT消息，可以保证当某条通道出现故障时重要的TT消息不丢失．接收端接收数据包后，根据时间标签过滤冗余数据，进行去冗余处理．通过上述的双冗余设计可以保证TT消息的可靠传输．

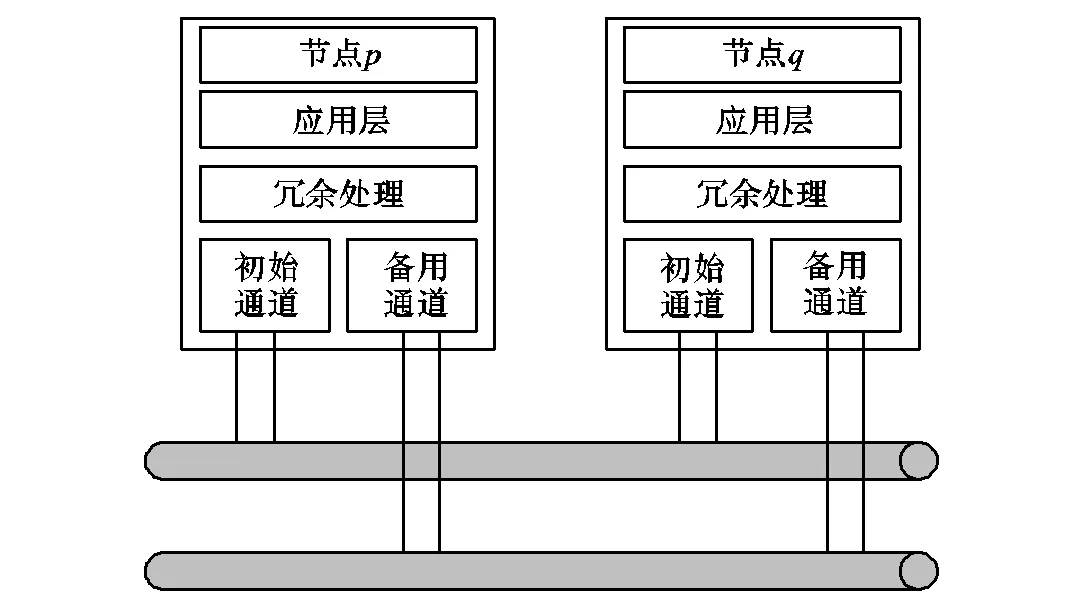
图9 双冗余拓扑结构

通过第2节的交换机优化和链路优化，得到优化后的集约结构，然后进行双冗余设计保证TT消息的可靠性．以图10(a)所示的结构为例，优化后的集约结构中含有两组TT流量(TT流涉及的交换机和路由在虚线框内)，分别是TT1：E1→S1→E3和TT2：E2→S2→S3→E4．使用节点冗余实现双冗余结构，如10(b)所示，以E1和E3为冗余节点，得到备用通道E1→S1′→E3，同理得到E2→S2′→S3′→E4．采用节点冗余方案的网络，调度表无需调整，能够保证TT消息的实时性和确定性．TT消息通过两条物理通道同时传输，TT1：E1→S1→E3；E1→S1′→E3和TT2：E2→S2→S3→E4；E2→S2′→S3′→E4．同时，非TT消息可以双通道分散传输．以E1和E3为源节点和目的节点的RC消息有：RC1、RC3、RC4．以E2和E4为源节点和目的节点的RC消息有：RC6．这4条RC消息可以在备用通道中传输，调整后RC消息的路由变为：RC3：E1→S1′→E3，RC4：E1→S1′→E3，RC6：E2→S2′→S3′→E4，RC1不改变．

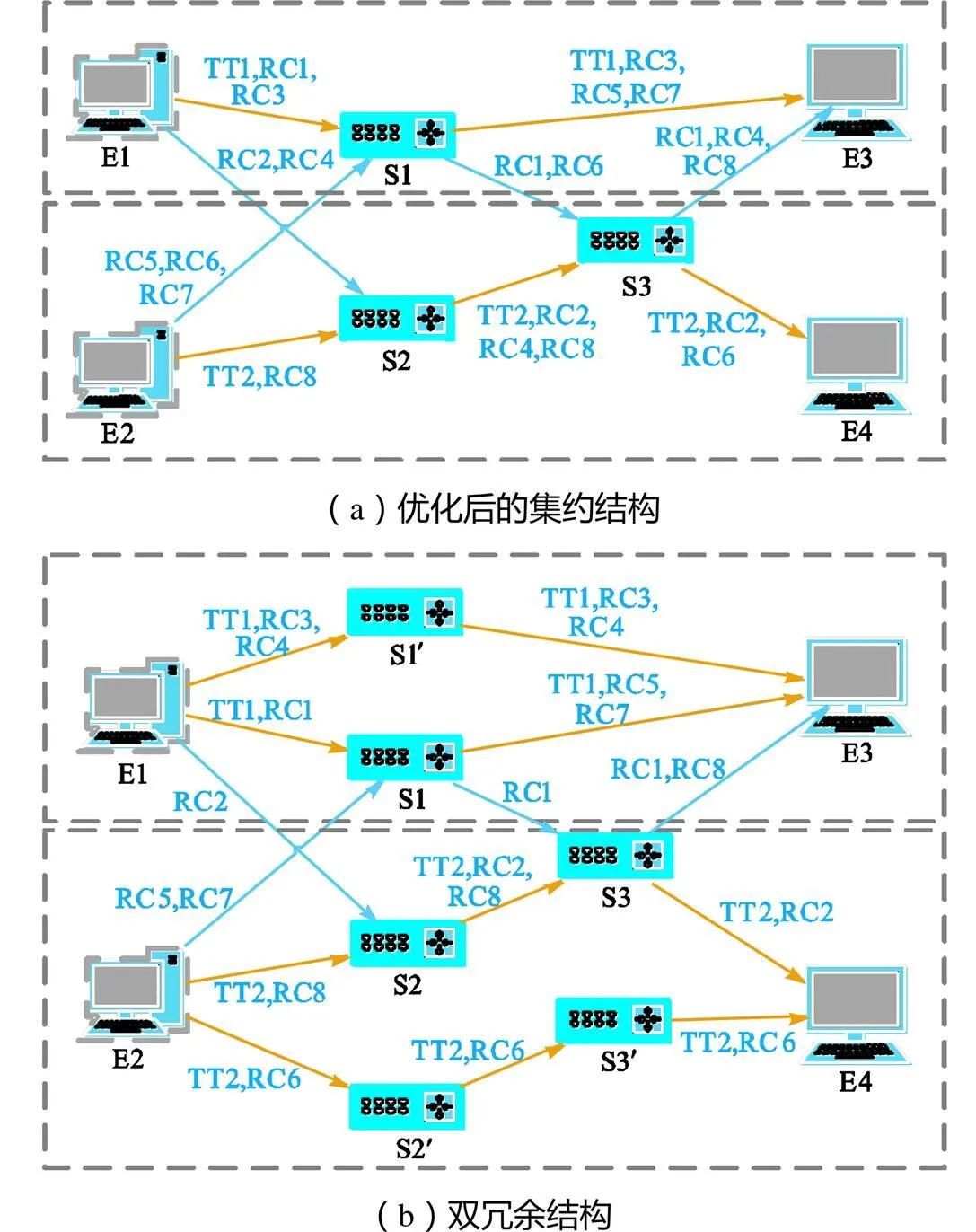
图10 TTE双冗余设计

对于双冗余的TTE网络，TT消息采用备份传输，非TT消息采用双通道分散传输．当双冗余的TTE网络发生故障时，可以自适应地实现具有零故障恢复时间的信息传输，无需网络故障冗余链路切换且丢弃窗口对网络延迟的影响可以忽略，从而可提高系统的实时性．

4 结果及分析

4.1 参数设置

给定网络参数如表1所示，用于计算目标函数的值，评价拓扑方案的网络延迟性能与架构成本的综合表现．

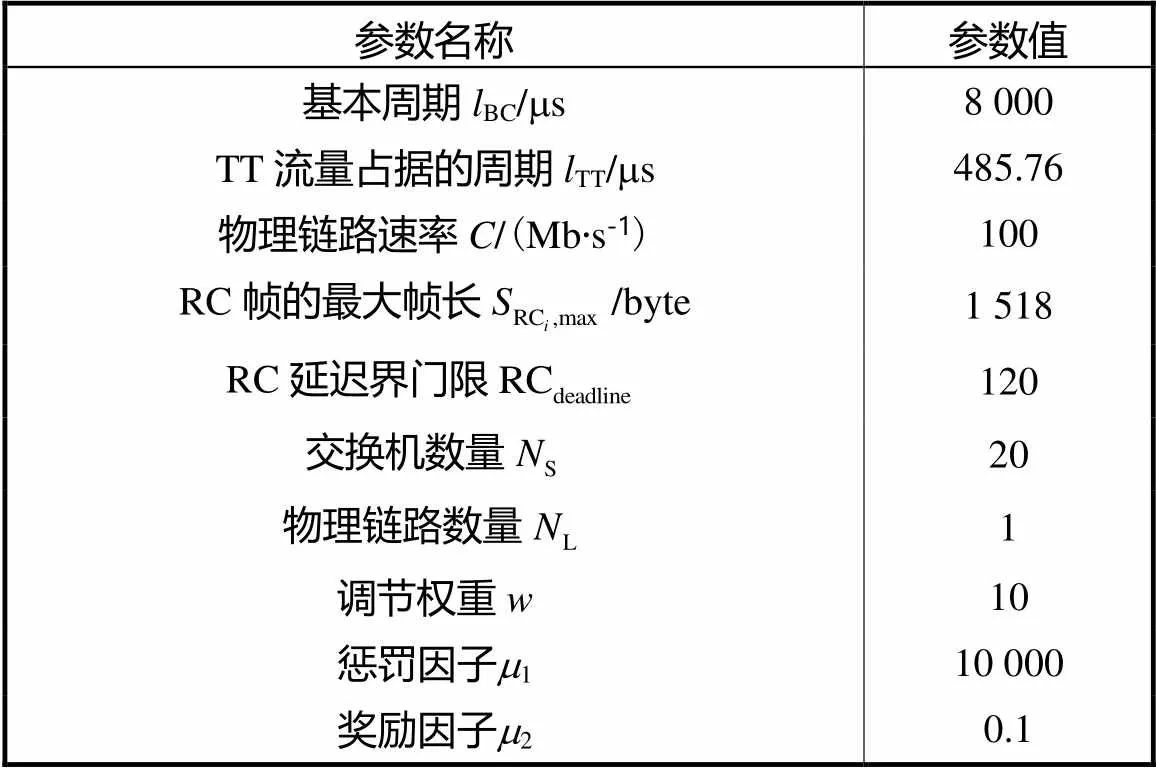
表1 参数设置

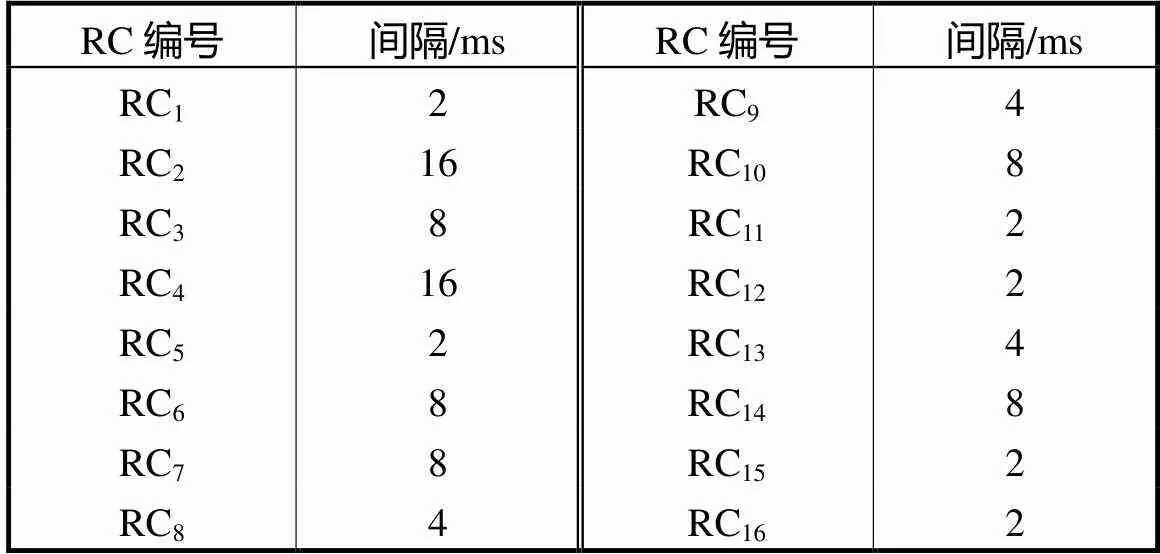
表2 RC流量带宽分配间隔

4.2 恢复策略对比

交换机删减后有3种恢复策略，策略1选择最小跳数按照初始路径直接进行链路重构，策略2选择被优化交换机的发送侧和目标侧的边缘节点进行链路重构，策略3不添加链路，直接调整路由．本文最终的拓扑恢复采用混合策略择优，即选择3种恢复策略对应目标函数值最小的一种．

仍以图4和图6给定的示例1和示例2为例，比较3种恢复策略的优劣．拓扑参数及采用不同策略恢复后的目标函数值如表3所示．示例1和示例2的通信任务相同，都包括3组TT任务和7组RC任务，TT任务和RC任务的源-目节点相同，例如3组TT任务的源-目对是E1→R1、E2→R1和E3→R3．此外，示例1和示例2的交换机数量和位置相同，但是链路的连接情况不同，示例1中交换机节点的介数的均值为5.17，介数方差为2.47，而示例2中的节点介数的均值为5.00，介数方差为6.67．由图5和图7可知，示例1的恢复策略3不可行，示例2的恢复策略3可行．3种恢复策略得到的拓扑结构目标函数如表3所示．

表3 恢复策略对比

由表3可知，示例1的最优恢复策略是策略1，示例2的最优恢复策略是策略2．表3中两组示例的通信任务相同，交换机数量和位置也相同，但由于物理链路的连接方式不同，导致两组示例的初始拓扑不同．两组示例的节点介数的均值约为5，通过物理连接，使得两组示例的节点介数的方差不同．示例1的方差小，各个节点发生拥塞的概率相差小；示例2的方差大，各个节点发生拥塞的概率相差大．示例2中恢复策略3占优的原因在于示例2的初始拓扑节点介数的方差比较大，通过策略2筛选出边缘节点连接被删除目标交换机的前后节点，边缘节点能够分担中心节点的传输压力．而示例1中的方差比较小，使用策略3筛选的边缘节点与中心节点的重要性相近，并不能起到很好的分担效果，因此不如采用策略1按照最小跳数进行链路重构．而采用策略3不需要额外添加物理链路，架构成本最为节省，但存在调整路由仍无法满足RC任务的情况，而且即便策略3可行，其网络延迟的表现是最差的．设计的算法采用混合策略，通过目标函数筛选出最优的恢复策略．

4.3 拓扑算法优化结果

由于恢复策略性能与网络拓扑和路由有关，因此全网的优化采用混合策略，用最终优化前后的目标函数对比说明本文提出算法的有效性．选取10组初始 拓扑和初始路由，其参数和优化前后的结果如表4 所示.

由表4可以看出，设计的最小介数节点删除及混合策略恢复的拓扑优化算法可以在满足网络延迟要求的前提下，牺牲少量的延迟性能，大幅降低架构成本．优化前后的总的目标函数对比如图11所示， 随机选10组初始路由和拓扑，验证所提算法的有效性.

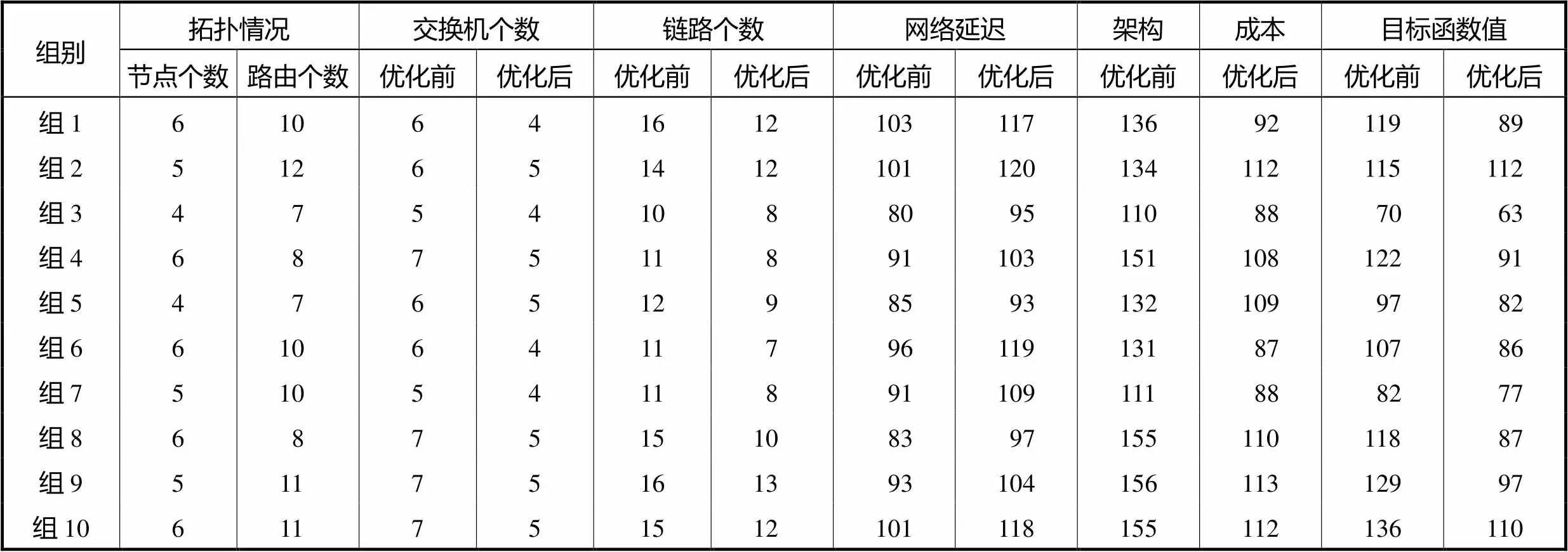
表4 优化前后结果对比

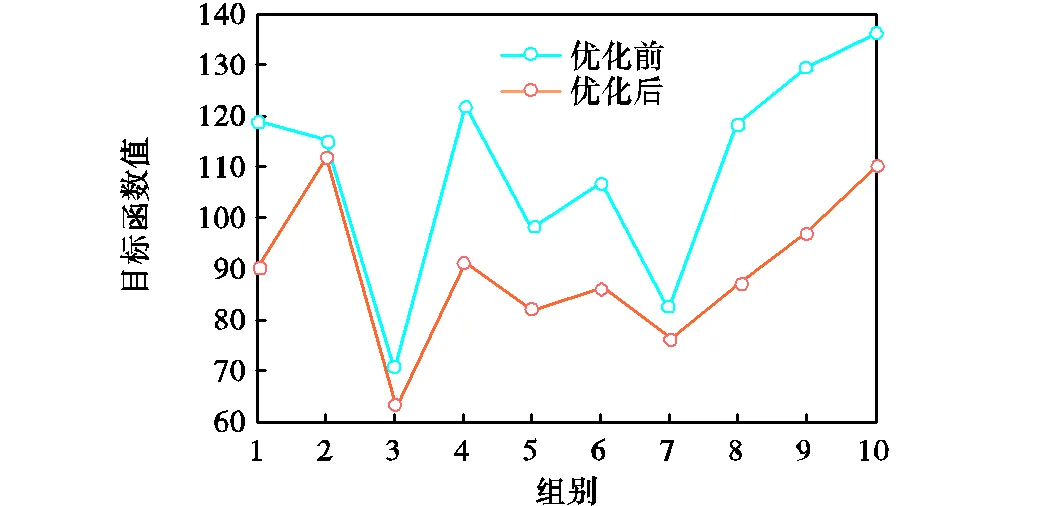
图11 10组路由表优化前后的目标函数值

5 结 语

本文提出了一种针对TTE网络的集约型拓扑优化方法．首先基于网络演算推导RC消息延迟上界，设计能综合评价延迟性能和架构成本的目标函数．然后提出最小介数节点删除及混合策略恢复的拓扑优化算法，并证明恢复策略性能与网络初始拓扑和路由有关，从而说明混合策略的优势．此外，通过目标函数筛选出最优的拓扑优化方案，并进行去冗余操作．最后，在优化后的集约拓扑基础上进行TT消息的双冗余设计，进一步保障TT消息可靠性并实现RC消息的分流传输．此方法结合了确定性网络的时延分析和冗余网络的优化策略，在保证TT消息准时传输和RC消息及时传输的情况下，简化网络，降低网络物理成本．

［1］ Steiner W. TTEthernet specification[S]. Wien：TTTech Computertechnik AG，2008.

［2］ Wang Q，Teng L P，Cui X，et al. TTE scheduling method based on adaptive dual redundancy and performance analysis[J]. Chinese Journal of Engineering，2019，41(3)：393-400.

［3］ 阴书玉. 基于ESO算法的多目标拓扑优化及其应用研究[D]. 太原：中北大学，2015.

Yin Shuyu. Research on Multi-objective Topology Optimization and Its Application Based on ESO Algorithm[D]. Taiyuan：North University of China，2015(in Chinese).

［4］ Beshley M，Seliuchenko M，Panchenko O，et al. Adaptive flow routing model in SDN[C]//2017 14th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM). Polyana，Ukraine，2017：298-302.

［5］ Lee D，Hong P，Li J. RPA-RA：A resource preference aware routing algorithm in software defined network [C]// 2015 IEEE Global Communications Conference (GLOBECOM). San Diego，USA，2015：1-6.

［6］ Noman H，Jasim M. A proposed linear multi-controller architecture to improve the performance of software defined networks[J]. Journal of Physics：Conference Series，2021，1773(1)：012008.

［7］ Zhang L，Lampe M，Wang Z. Multi-objective topology design of industrial ethernet networks[J]. Frequenz，2012，66(5/6)：159-165.

［8］ 王红春. 面向DIMA应用的时间触发以太网性能优化与评估技术研究[D]. 西安：西安电子科技大学，2019.

Wang Hongchun. Research on Performance Optimization and Evaluation Technology of Time-Triggered Ethernet for DIMA Application[D]. Xi’an：Xidian University，2019(in Chinese).

［9］ Abdel B，Mohamed R，Abouhawwash M. Balanced multi-objective optimization algorithm using improvement based reference points approach[J]. Swarm and Evolutionary Computation，2021，60：100791.

［10］ Motter A E. Cascade control and defense in complex networks[J]. Physical Review Letters，2004，93(9)：098701.

［11］ Huang W，Chow T W S. Effective strategy of adding nodes and links for maximizing the traffic capacity of scale-free network[J]. Chaos An Interdiplinary Journal of Nonlinear Ence，2010，20(3)：033123.

［12］ Jiang Z Y，Liang M G，Guo D C. Improving network transport efficiency by edge rewiring[J]. Modern Physics Letters B，2013，27(8)：1350056.

［13］ Hu K，Liu C，Hu T，et al. Enhancing traffic capacity for scale-free networks by the one-way links[J]. Journal of Physics A—Mathematical & Theoretical，2010，43(17)：175101.

［14］ Nikolaus P，Schmitt J，Schütze M. H-mitigators：Improving your stochastic network calculus output bounds[J]. Computer Communications，2019，144：188-197.

［15］ Wang H，Hu J Q，Niu W S. RC performance analysis based on model optimization with the aid of network calculus[J]. Photonic Network Communication，2019，37(2)：253-260.

［16］ Zhao L X，Pop P，Li Q，et al. Timing analysis of rate-constrained traffic in TTEthernet using network calculus[J]. Real Time Systems，2017，53(2)：254-287.

［17］ Jin D，Ryu J，Park J，et al. Bounding end-to-end delay for real-time environmental monitoring in avionic systems[C]// 2013 27th International Conference on Advanced Information Networking and Applications Workshops. Barcelona，Spain，2013：132-137.

［18］ Gutiérrez J J，Palencia J C，Harbour M G. Holistic schedulability analysis for multipacket messages in AFDX networks[J]. Real-Time Systems，2014，50(2)：230-269.

［19］ Finzi A，Mifdaoui A，Frances F，et al. Network calculus-based timing analysis of AFDX networks with strict priority and TSN/BLS shapers[C]//2018 IEEE 13th International Symposium on Industrial Embedded Systems(SIES). Graz，Austria，2018：1-10.

［20］ Xiang Y，Wang W，Zhang X，et al. Performance research on time-triggered ethernet based on network calculus[J]. EURASIP Journal on Wireless Communications and Networking，2014，2014(1)：1-9.

［21］ 赵露茜，李 峭，林晚晴，等. 基于随机网络演算的TTE网络时延分析[J]. 航空学报，2016，37(6)：1953-1962.

Zhao Luxi，Li Qiao，Lin Wanqing，et al. Stochastic network calculus for analysis of latency on TTEthernet network[J]. Acta Aeronautica et Astronautica Sinica，2016，37(6)：1953-1962(in Chinese).

Intensive Time-Triggered Ethernet Topology Optimization

Wang Qing1，Wu Chenbang2，Chen Peng1，Zhou Hu3，Wu Zhiliang4

(1. School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin International Engineering Institute，Tianjin University，Tianjin 300072，China；3. Beijing Aerospace Automatic Control Institute，Beijing 100070，China；4. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

Time-triggered ethernet(TTE)is a new technology of ethernet network communication，combining time-triggered and event-triggered traffic. This technology is compatible with the standard ethernet protocol，guarantees the certainty and reliability of time-triggered traffic，and has significant advantages in aerospace communication applications. However，the high cost of space networks limited the development of TTE to a great extent. Therefore，the study of intensive network topology can reduce the cost of system architecture. First，this paper introduced the complex network theory and established the problem model of a simplified network topology through a rate-constrained message delay threshold. Then，a topology optimization algorithm based on the deletion of the minimum number of nodes and mixed strategy recovery was proposed，converging to a state where the objective function was minimized using alternating iterations of nodes and edges. Finally，a dual redundancy structure was designed based on the optimized intensive network，improving the reliability of the time-triggered business. The optimization of objective function comparison shows that the proposed method can simplify the network topology and reduce the architecture cost when considering the time delay. This research provides the optimization algorithm and recovery strategy of real-time aerospace communication equipment deployment based on TTE. The algorithm and the strategy can be used to upgrade and optimize the old network deployment. The modeling and topology optimization process in a random Barabási-Albert scale-free network is explained by examples. The algorithm idea and the design method can be further applied to network topology optimization on a larger scale，which provides references for space communication network optimization.

time-triggered ethernet；topological optimization；cost of architecture；network delay；double redundancy design

V19

A

0493-2137(2022)09-0942-11

10.11784/tdxbz202101025

2021-01-14；

2021-03-09.

汪 清（1982— ），女，博士，副教授，wangq@tju.edu.cn.

陈 鹏，Chenpeng_1997@tju.edu.cn.

民用航天预研基金资助项目.

the Advanced Research Foundation of Civil Aerospace.

(责任编辑：王晓燕)