3阶FLFB低通滤波器的最小可接受功耗分析

张旭东，雷倩倩，张芳玲，李 弦，李连碧

（1. 西安工程大学理学院，陕西西安 710000；2. 深圳市纽瑞芯科技有限公司，广东深圳 518000）

1 引言

电路设计中常使用高阶的滤波器来提供大的带外抑制. 实现高阶滤波器的方式有2 种，一是多级级联［1～3］，电路实现较简单，但在通带内对工艺更敏感；二是多重反馈［4，5］（Multiple-loop FeedBack，MFB），通过对每一级都采用负反馈连接来构成高阶滤波器，结构较复杂，但对工艺的敏感度较低，且其中的FLFB（Followthe-Leader-FeedBack）结构还具有良好的噪声性能［6］.

无论是级联还是多重反馈，高阶的滤波器都会引入较大的功耗，作为收发机中的重要模块，如何减小功耗一直是设计师需要考虑的问题. 在工艺确定的前提下，滤波器的功耗优化一般分为2 大类：晶体管级的优化和拓扑级的优化. 晶体管级的优化重心在运放上，文献［7］采用以反相器为基础的单级跨导放大器来替代传统的多级运放，并通过衬底反馈技术，降低了金属氧化物半导体场效应晶体管（Metal-Oxide-Semiconductor Field-Effect Transistor，MOSFET）的阈值电压，实现了一款0.4 V、65.6µW的3阶复数带通滤波器；文献［8］基于超级源跟随器来构建积分单元，实现4阶、33 MHz、1.38 mW的低通滤波器. 而拓扑级的优化重心则在滤波器的结构上，对于有源RC的低通滤波器，在每一个运放的输出端与反馈电阻之间加上起到隔离负载效果的源跟随器，降低了运放负载驱动能力的要求，使用单级运放级联可实现4 阶、0.5 mW、0.6 MHz 的低通滤波器［9］；也可以利用无源器件综合出多个极点，通过减少有源器件的使用个数来达到降低功耗的目的［10，11］；或者通过降低电源电压来减小功耗，文献［12］中通过增加输入共模反馈（Input Common-Mode FeedBack，I-CMFB）偏置电路，在保证直流工作点正常的情况下减小了运放的输入参考电平，进而降低了运放可接受的最小电源电压，以0.55 V 的电源电压实现了4阶、11.3 MHz的模拟基带滤波器.

这些优化设计虽然达到了降低功耗的目的，但对于多极点系统，为了保证系统的稳定性，常常采用相位裕度大于60°的电路设计，这种设计方法虽然稳定性较高，但存在相位裕度冗余. 本文针对多重反馈中的3 阶FLFB 有源RC低通滤波器，提出了一种最小可接受功耗的分析方法，在保证系统稳定的前提下降低了相位裕度冗余，并给出了滤波器设计参数与功耗之间的关系图. 从环路稳定性入手，以劳斯-赫尔维茨（Routh-Hurwitz，RH）稳定性判据为基准，分析了当滤波器处于稳定临界状态时，不同设计参数的滤波器所能接受的最小功耗，并对其进行了电路级仿真验证.

2 3阶FLFB低通滤波器稳定临界状态分析

2.1 最小可接受相位裕度

3 阶FLFB 低通滤波器拓扑结构如图1 所示，Vin为滤波器输入端，Vout为滤波器输出端，A（s）为运放的增益，Q为滤波器品质因子，R、C分别为电阻、电容. 当考虑运放的有限增益、有限带宽时，滤波器的传输函数TF（s）可用式（1）来表示，其中D（s）可以用式（2）表示.

图1 3阶FLFB低通滤波器拓扑结构

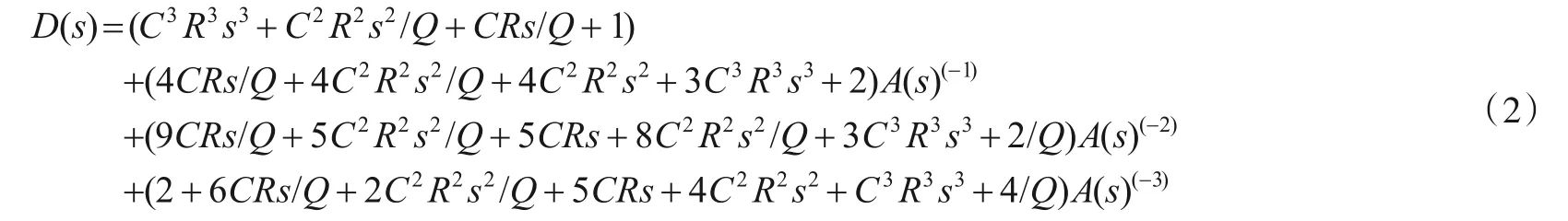
为了进一步推导出滤波器对运放的设计要求，考虑双极点系统，高频下运放的增益A（s）可用式（3）来表示

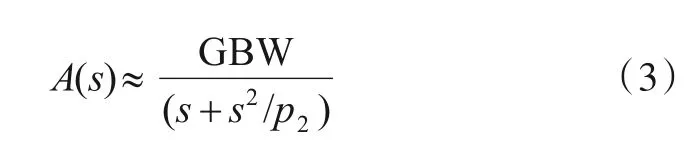
其中，p2为运放的次极点，GBW 为运放的单位增益带宽，将式（3）代入到式（2）中，得到一个以s为变量的9阶多项式，见表达式（4），其中a9～a0的详细表达见式（5）.

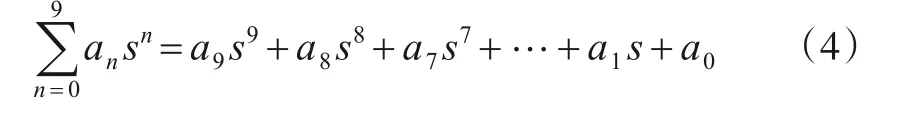
以a9～a0作为基准元素，而第i行第j列的元素可表示为式（6），推导至只有一个有效元素，其余皆为0的一行，就形成了表达式（7）所示的劳斯-赫尔维茨阵列.

当劳斯-赫尔维茨阵列满足以下条件：a. 式（4）中每一项系数a9～a0皆为正数；b. 阵列左边第一列元素皆为正数. 那么式（4）所对应的系统便是稳定的［13］. 为了更直观地描述稳定性，将双极点系统下运放的相位裕度代入到表达式（4）中.

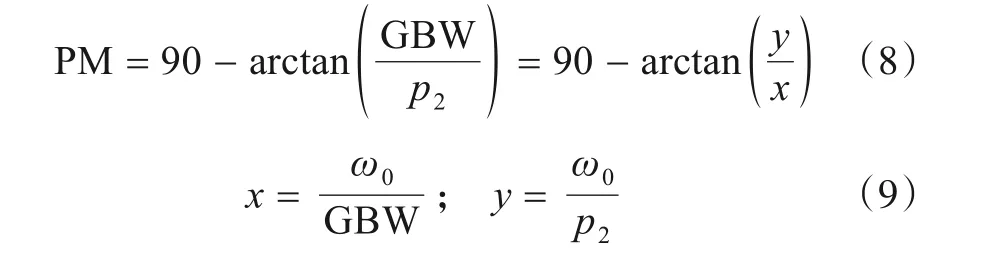
式（8）为运放相位裕度（Phase Margin，PM）的表达式，单位为度（degree），其中的x，y可表示为式（9），其中，ω0为滤波器的截止频率. 设滤波器的3个极点均为实极点，当忽略运放的非理想性时，滤波器的截止频率为

将式（9）、式（10）代入到式（5）中，用x，y替换掉p2、GBW，推导出劳斯-赫尔维茨阵列，令RH9，1=0，给定Q，x的值，解得满足判据b 的y的解，进而通过式（8）得到运放的PM. 此时RH9，1=0，滤波器处于稳定临界状态，如果运放的相位裕度小于此时计算的值，则滤波器存在不稳定的风险，故可称此时计算的相位裕度为最小可接受相位裕度（Minimum Acceptable Phase Margin，MAPM）［14］. 通过MATLAB 进行数据处理，拟合出3 阶FLFB 低通滤波器的参数与MAPM 的关系图，如图2 所示，从图中可以看到，ω0/GBW 越小，Q取值越大，所需要的PM越小，滤波器越容易稳定.

图2 最小可接受相位裕度

2.2 最小可接受功耗

通过稳定性判据得到了最小可接受相位裕度，继而可以分析出运放的最小可接受跨导，通过进一步的电路分析和仿真验证，拟合出滤波器参数与功耗的曲线图. 本次设计采用的是Class AB 两级运放，如图3 所示. 运放包含3 部分，分别是两级放大电路、共模反馈电路（the Common-mode Feedback）以及偏置电路（the Reference circuit），通过小信号分析，运放的增益也可表示为式（11）.

图3 Class AB两级运放电路图

其中，gPM和gNM表示MOS 管的跨导，R1、R2分别表示第一级、第二级的输出阻抗，A、A1、A2分别表示运放的总增益、第一级增益以及第二级增益，而此时极点表示为

式（12）、式（13）中CC、Cload分别为密勒电容、负载电容，p1由于具有较大的电容成为运放的主级点［15］，p2即为次级点，再参考式（8），即可得到运放中第一级跨导Gm1与第二级跨导Gm2的表达式：

接着利用2.1 节计算的数据，令ω0中的R、C分别取10 kΩ、1 pF，计算得到运放的最小可接受跨导（Mini⁃mum Acceptable Transconductance，MAT）分析图，如图4所示，其中图4（a）为第一级跨导Gm1，图4（b）为第二级跨导Gm2. 从图4中可以看到，当Q取值接近0.3时，可接受的最小跨导值较小，这是因为此时滤波器的ω0接近1/RC，提高了无源器件的实际利用率，减小了对运放GBW的要求，降低了功耗.

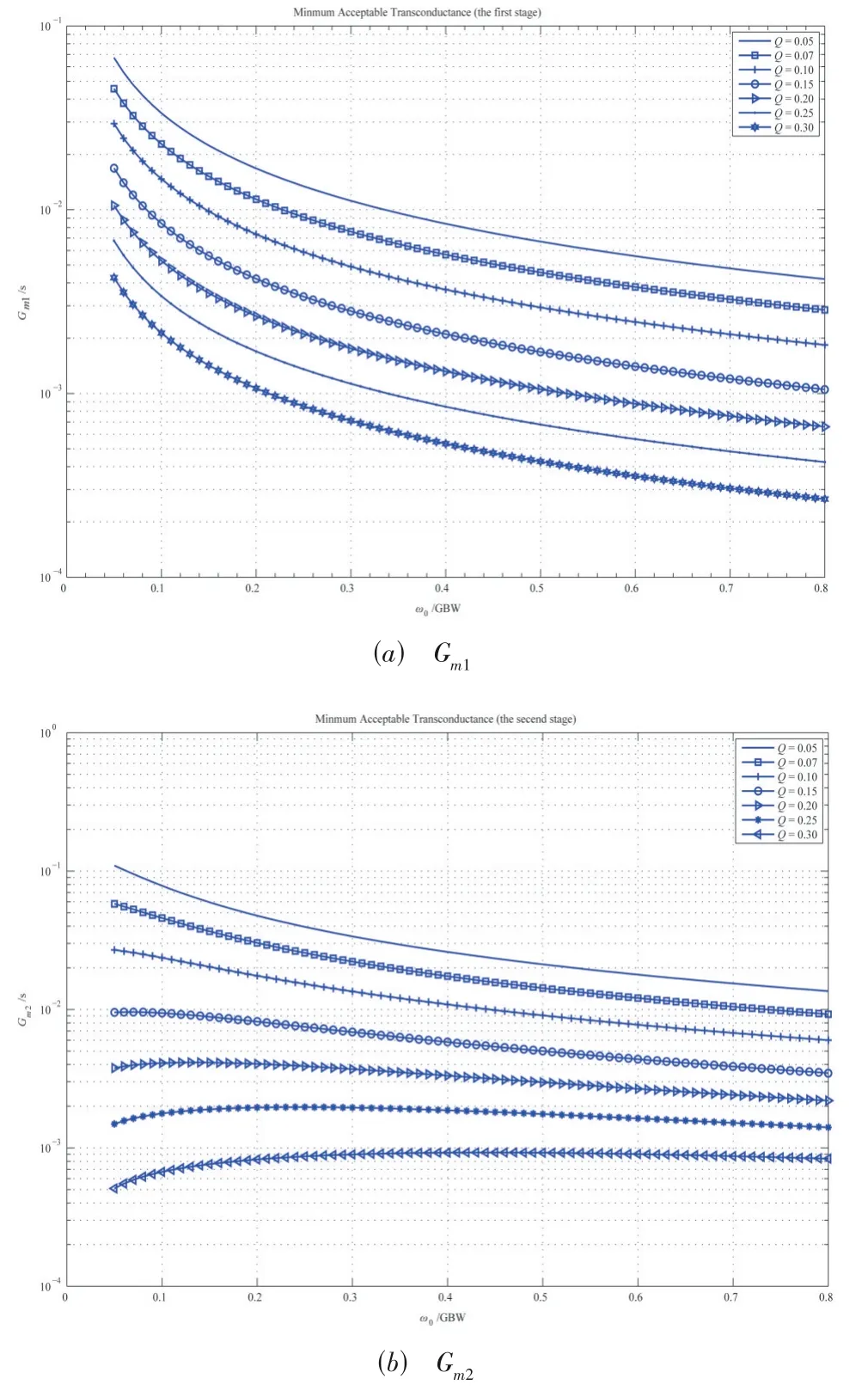
图4 最小可接受跨导分析图

为了进一步分析相位裕度对运放功耗的影响，在电路设计中，通过改变运放的第二级跨导Gm2，也就是图3中PM6，NM7晶体管的尺寸来分析功耗和GBW 的变化. 如图5 所示，可以看到，随着横坐标轴PM 从60°变化到10°以下，左纵坐标轴的功耗从164 µA 减小到84 µA，右纵坐标轴运放的GBW 也随之从50 MHz 降低到了30 MHz.

对应于运放受PM 的影响，在典型的工艺角下对滤波器同样进行电路仿真、数据采集，拟合出图6 所示滤波器参数与功耗之间的关系图. 以功耗为横坐标轴，范围为242～482 µA，对应于图5 中PM 的变化范围7.9°～60°，图6 中从上到下3 条曲线依次对应着Q取0.3，0.2，0.1 时滤波器的有效带宽与功耗的关系.可以明显看出，在相同功耗下，Q取0.3 所对应的滤波器带宽更大，变化范围为5.24～11.33 MHz，为了进一步验证最小可接受功耗理论的可行性，选取运放PM=37.9°（图6中B点）的晶体管尺寸，进行版图设计及后仿验证.

图5 运放PM对功耗和GBW的影响

图6 滤波器的参数Q、ω0与功耗之间的关系

3 后仿验证

为了验证最小可接受功耗分析方法，采用UMC 40 nm CMOS 工艺，设计了一款3 阶FLFB 低通滤波器，如图7 所示，版图总面积为0.14×0.23 mm2，其中5 位控制字的调谐电容面积占比超过了50%，3 个运放采用相同的电路结构（Opamp1～3）. 在电源电压1.0 V、负载电容2 pF 的情况下，运放性能参数如表1 所示，可以看到不同工艺角下运放的相位裕度不同，那么相对应的ω0/GBW 也会不同，以TT，27 ℃工艺角为例，对滤波器进行后仿验证.

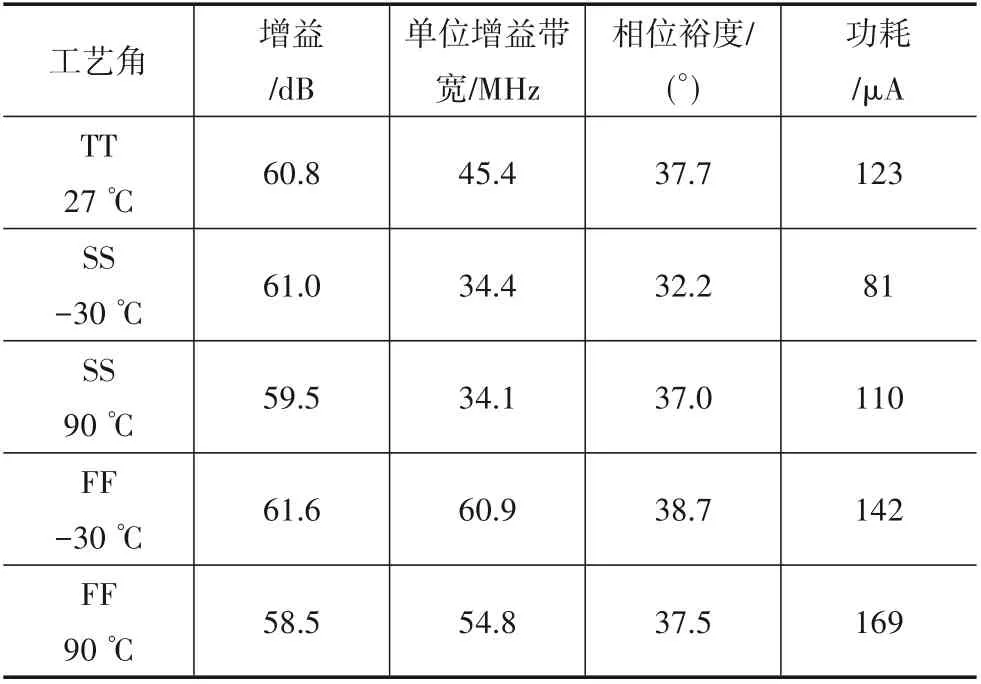
表1 不同工艺角下运放性能参数

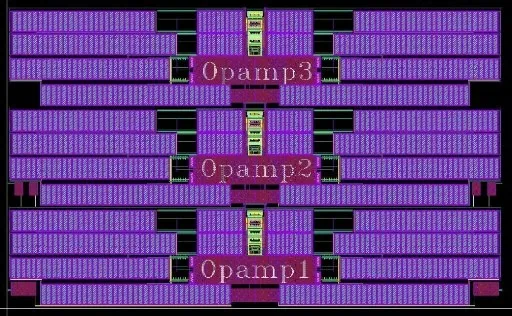
图7 3阶FLFB低通滤波器版图

为了验证最小可接受功耗分析方法的稳定性，并验证滤波器的带宽是否为有效带宽，对滤波器进行瞬态仿真. 令电源电压在10 µs 时上电，1 µs 后稳定在1.0 V，调节控制字从00000 到00100 变化，得到图8所示的滤波器输出瞬态响应曲线. 图中自上而下对应滤波器3 dB 带宽分别为17.09 MHz，17.74 MHz，14.35 MHz，11.21 MHz，9.96 MHz，而此时对照图2中Q=0.30 的曲线，当相位裕度为37.7°时，ω0/GBW=0.33，此时运放GBW=45.4 MHz，发现电容取0.25 pF，0.5 pF 时ω0/GBW>0.33，滤波器存在不稳定的风险，与图8 中仿真结果相吻合；接着对滤波器进行全控制字仿真，滤波器输出幅频响应曲线如图9 所示，图中蓝色圆圈部分可以看到明显突起，右上角为放大后的图示，发现0.75 pF，1.0 pF 所对应的曲线通带内突起超过1 dB，故舍去. 选取有效调谐电容1.25～8 pF，此时滤波器的实际ω0为0.88～9.96 MHz.

图8 滤波器输出瞬态响应曲线

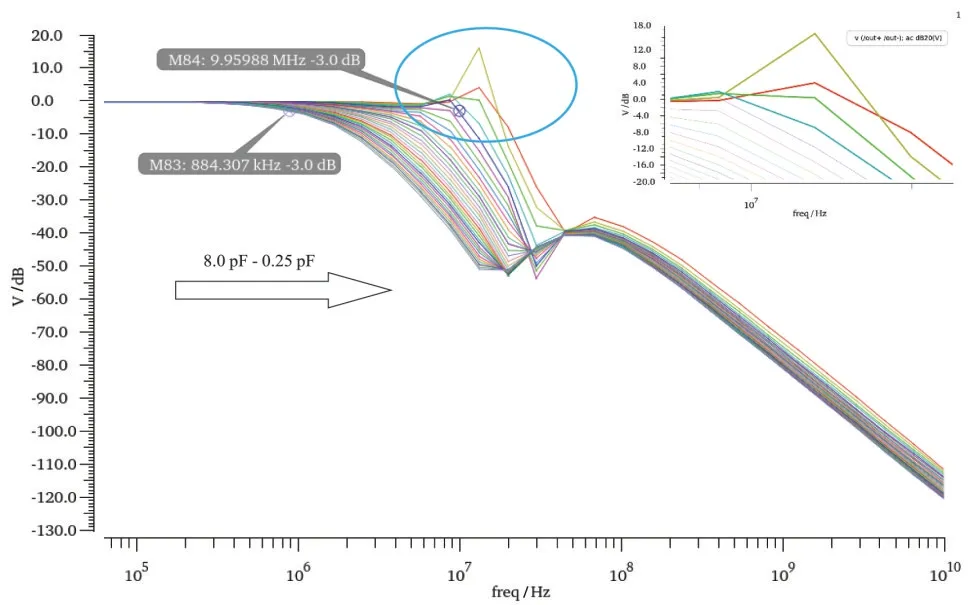
图9 滤波器全控制字下频率响应曲线

表2 为本文与参考文献的性能指标对比. 本文设计的3阶FLFB低通滤波器有效带宽为9.9 MHz，此时运放的PM=37.7°，以图6中B 点为参考：PM=37.9°，Power=326 µA，与传统设计的功耗482 µA 相比较，减小了近30%. 并且为了客观对比，进行了品质因数、单阶滤波器功耗（功耗/极点数）的计算，从表中看到，本次设计的品质因数小了一个量级，并具有噪声优化效果，验证了最小可接受功耗理论的可行性，但线性度较差，这是因为电流太小引起的输入转换速率低，进而造成了信号失真，可以以功耗为代价来优化线性度.

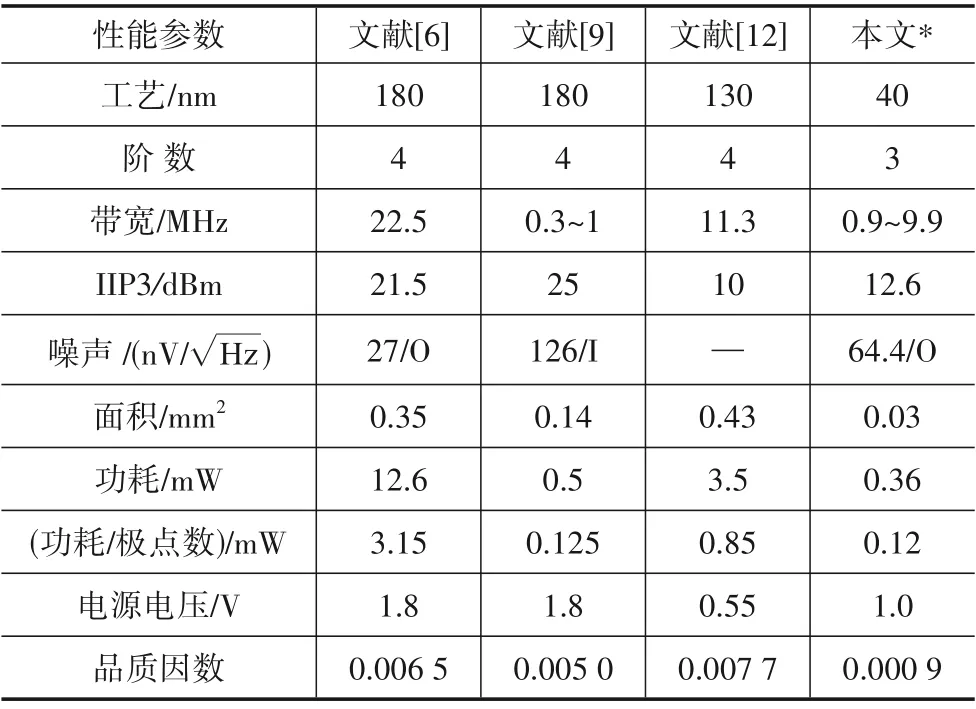
表2 性能指标对比

4 总结

本文针对一款3 阶FLFB 低通滤波器，根据劳斯-赫尔维茨稳定性判据，当滤波器处于稳定临界状态时，使用MATLAB 拟合出了滤波器的最小可接受跨导图，给出滤波器的参数与最小可接受功耗之间的关系，并进行了仿真验证，证实了最小可接受功耗分析方法的有效性. 需要指出的是，本文中的设计在实际应用中还需要对滤波器进行进一步的性能优化，比如以增大功耗为代价来增大滤波器的带宽、线性度. 除此之外，本文的分析方法以及针对3阶FLFB的最小可接受跨导分析图、参数与功耗的关系图可以为低功耗滤波器的设计者提供一定的参考.