基于小波模极大值和自适应Canny算子的织物疵点检测算法

陈玉婷，刘洞波，施怡澄，高樱萍

（湖南工程学院 计算机与通信学院，湘潭 411104）

0 引言

由于人工识别疵点成本高、检测效果不理想，因此提出了各种基于机器视觉的织物疵点检测方法［1］.织物疵点与疵点背景的边缘特征是检测织物缺陷的关键特征［2］，并且Canny 算子检测精度高、信噪比大，因此在进行疵点检测时选择Canny 算子［3］对织物图像进行边缘检测.针对Canny 算子的高斯函数标准差和高低阈值需要人为设定的问题，胡克满等［2］提出了一种自适应Canny 边缘检测算法，自适应高斯滤波与图像阈值选择；闫伟伟等［4］运用双重基本全局阈值分割算法，根据实时的光照变化自适应地确定高低阈值；李亚利［5］提出一种自适应滤波，滤波时对图像进行局部加权以及原始信号迭代卷积，每次迭代都会改变加权系数；张升等［6］提出了结合双重Otsu 方法进行高低阈值确定的算法.另一方面，频谱分析方法也常被应用于边缘检测，其中小波变换［7］是为了解决傅里叶变换只能全局操作的问题，小波变换能够在空间和频域进行局部变换，从而反映信号局部特征，也能够对信号进行多分辨率分析［8-9］.管声启等［10］提出一种小波域高斯差分滤波起球疵点评价的算法，具有较强的抗干扰能力；厉征鑫等［11］提出以单演小波分析工具为基础的织物疵点检测算法.由于噪声和疵点的边缘是图像中的高频分量，Canny 算子只能获得图像中的低频分量，易丢失正确边缘.赵静等［12］融合改进Canny 算子和小波模极大值法的图像边缘检测方法，小波模极大值法通过从多方向取值的方式获取局部模极大值，保留高频边缘的同时将边缘与噪声分离，边缘图像具有较好的连续性，然而目前该方法的研究只局限于理论层面，未应用于织物疵点检测领域.

为解决经典Canny 算子参数需人为设定问题，并同时保留高频边缘，本文将采用自适应高斯滤波和最大类间方差法自适应获取阈值实现Canny 算子的改进，并且结合小波模极大值算法对不同类型的布匹瑕疵点进行检测.分别用上述两种方法来实现对边缘的提取，再将两个边缘图像进行融合并优化处理.

1 疵点检测原理

本文算法总体流程如图1 所示.

图1 本文算法总体流程图

1.1 自适应Canny边缘检测

Canny 算子是一个多级边缘检测算法，实现过程主要包括四个步骤：图像降噪、计算图像梯度向量与梯度幅值、极大值的选择与非极大值抑制、双阈值筛选［2］.在实现过程中图像降噪和双阈值筛选是两个重要环节，其中图像降噪时采用的高斯函数标准差σ 和双阈值筛选时的高阈值maxVal 与低阈值minVal 需要人为设定，在一定程度上限制了自动化的疵点检测处理.针对上述参数，提出一种自适应Canny 边缘检测算法.

1.1.1 自适应高斯滤波

经典Canny 边缘检测算法进行高斯滤波时，高斯函数标准差σ 需要人为设定，为了解决这个问题，在N*N 窗口中，将残差作为选取σ 的度量标准之一.这样就使平滑后的图像能够保持细节信息.本文算法中的自适应高斯滤波是要在最平滑的结果和最佳保持细节信息的结果中取一个折中方案.σ 的计算方法为：

式（1）中，当c/σ2与ε2取最小值时的σ 为最优的参数值，其中ε 为残差.假设一幅二维图像的高斯滤波函数表示为：

在（x，y）像素点处，I0（x，y）为原始图像（x，y）点处灰度值；Iσ（x，y）为通过高斯滤波得到平滑后（x，y）点处灰度值；εσ（x，y）为（x，y）点处灰度值的残差.式中c 为常数，当σ 尽可能大时，能够尽可能得到平滑的结果，使得c/σ2取最小值.ε 随着像素点灰度值的变化而变化，通过高斯滤波后，（x，y）点处灰度值变化较小时，ε 的值较小.

1.1.2 自适应高低阈值获取

在对织物疵点进行检测时，非极大值抑制后，经典Canny 算法的阈值需要人为设定，不同的阈值会影响到图像边缘检测的效果.所以经典Canny 算法无法满足织物疵点在线检测要求，实时性及精确性较差.

本文使用Otsu 提出的一种自适应阈值确定方法，即最大类间方差法.该算法按照图像的灰度特性，设定一个阈值t，将图像所有像素分为前景C1和背景C2两类，在图像中占比分别为P1和P2，这两类像素的灰度均值分别为m1和m2，则图像全局灰度均值mG为：

类间方差S 为：

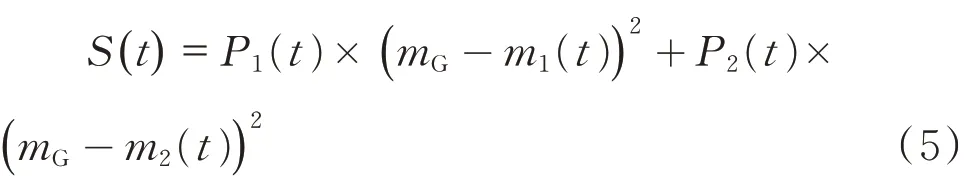
假定t0为最佳阈值，当t 取t0时，图像前景与背景的方差最大，即此时前景与背景差异最大.设t0为双阈值中的高阈值τh，则低阈值取值为τl＝τh/2.

1.2 小波模极大值算法

本文提出的基于小波模极大值的疵点检测算法的步骤为：多尺度小波分解，获取边缘点，去除噪声点.一幅织物疵点图像f（x，y）的梯度矢量为：

该梯度为f（x，y）在（x，y）点的最大变换方向.设（x1，y1）点沿着最大变换方向的一维邻域（x，y）＝（x1，y1）+λ∇（x1，y1）变化，当|λ|充分小时，该点可以取得局部极大值，则称（x1，y1）是f（x，y）的一个边缘点［13］.对于一个二维平滑函数θ（x，y），需要满足以下三个条件［14］：

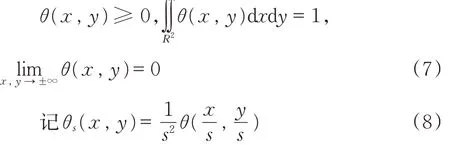
式（8）中s＝2j 表示小波变换的平滑尺度.在尺度s 下x，y 两个方向上的二维小波为：

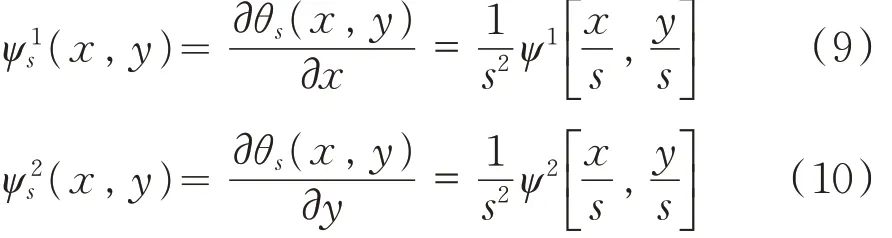
在尺度s 下，经平滑函数θs（x，y）处理疵点图像f（x，y）小波变换的2 个分量可表示为：

式（11）中，W1f（s，x，y）表示f（x，y）沿水平方向的梯度矢量；W2f（s，x，y）表示f（x，y）沿垂直方向的梯度矢量.另外，对应模值以及梯度方向可分别表示为：

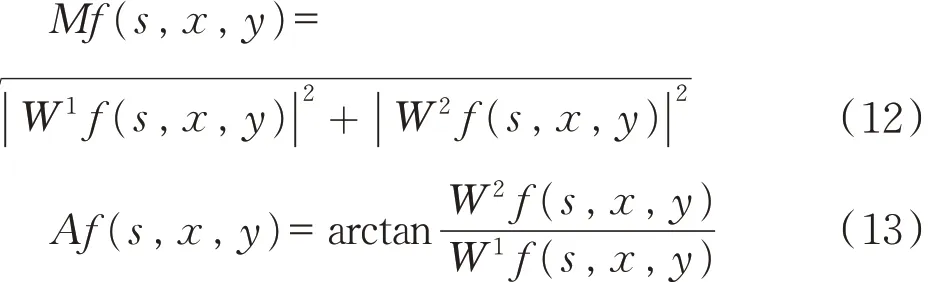
M 的模值大小反映了 f*θs（x，y）在（x，y）上的灰度变化程度 . Mf（s，x，y）在梯度方向Af（s，x，y）取极大值的点对应着f（x，y）的奇异点，即对于图像上的点（x，y），要确定其小波变换系数的模局部极大值点，对于该点的 8 领域点，从四个方向（0°,45°,90°,135°）上点（x，y）所在梯度方向上考虑它是否为该方向上极大值点.如果是，该点就是此梯度方向上模为局部极大值的点，则称之为这个图像的一个边缘特征点.所以只需记录这些模极大值点的坐标以及其相对应的模和角度，极大值点的集合即为图像边缘.

由于图像噪声也会产生小边缘，需要设定阈值消除噪声影响，局部模极大值大于阈值的点被保留为边缘点，小于阈值的为非边缘点，则不保留.具体方法是先对变换后整体小波系数模值进行非极大值抑制，再按比例得到阈值.得到边缘点后，将边缘点连接起来得到边缘图像［15］.

1.3 融合规则

将Canny 算法的边缘检测图像与小波模极大值法的边缘检测图像进行加权结合，生成最终边缘图像 .设 Canny 算法的边缘检测图像为 P（i，j），小波模极大值法的边缘检测图像为Q（i，j），结合后的边缘图像为T（i，j），算法公式为：

其中，α 为加权因子.Canny 算法提取图像边缘时，需要先平滑图像，得到的图像边缘为低频边缘.而小波模极大值对信号奇异性极为敏感，能够得到清楚的高频边缘轮廓.所以适当提高小波模极大值的边缘图像权重，并将两幅边缘图像的对应像素乘以加权因子后相加，得到最终边缘图像［12］.

1.4 数学形态学图像处理

获取疵点图像的边缘图像后，有一些像素点灰度值变化很大，但这些点不是疵点边缘，用数学形态学消除非边缘区域.设定一个阈值ATh，遍历整幅边缘图像，将已检测边缘并且二值化的图像中，面积小于ATh的小区域融合到周围的大区域中.具体做法为：对边缘图像做8 连通域操作，去除那些像素数据小于ATh数目的白色区域，将这些像素点全部置为0，变为黑色.

2 实验结果与分析

为了检验本文算法的效果，选取TILDA 标准织物图像库中破洞、切口、油污、飞丝等尺寸为256*256 像素的织物疵点图像进行实验，实验基本配置为 i7-10700 CPU 和 32 GB 内存，Windows10 操作系统，在MATLAB2018b 环境进行编译，采用Canny 算子、小波模极大值法和本文改进后的算法对织物图像分别进行实验，得出检测结果，检测结果如图2 所示.图2（a）是织物疵点原图，图2（b）是经典Canny算法的检测效果图，图2（c）是改进的自适应Canny算法的检测效果图，图2（d）是小波模极大值算法的检测效果图，图2（e）是本文算法的检测效果图.

图2 织物疵点检测结果对比图

实验时取α＝0.3、面积阈值ATh＝10 时融合效果较好.

可以看出，采用经典Canny 算法进行织物疵点的边缘检测时，边缘信息容易受到织物纹理信息与噪声信息的影响，说明人为设置的标准差和阈值不是最优参数，易产生伪边缘.经过自适应平滑和自适应阈值选择的Canny 算法可以检测出大部分的疵点边缘，但从疵点类型为断经这一类可以看出，容易丢失正确的疵点边缘信息.小波模极大值算法做织物疵点边缘检测时，也会受到噪声的影响，而且存在断续边缘的现象.将自适应Canny 算法和小波模极大值算法融合之后的本文算法保留了两者的优点，从本文算法的检测效果可以看出，织物疵点与背景纹理分割明显，检测出的边缘连续性得到了提高，边缘完整性得到了增强，同时还能有效去除图像中的噪声，具有很好的鲁棒性.

从表1 可以得出，对于同一组织物疵点图像，本文算法处理疵点图像的平均检测时间为1.098 s/张，自适应Canny 算法处理疵点图像的平均检测时间为0.671 s/张.本文算法的检测时间多于自适应Canny 算法，这是因为本文算法融合了小波模极大值算法并且进行了优化处理，计算量变大增加了检测时间.但本文算法的检测效果优于自适应Canny算法与小波模极大值算法单独使用，与自适应Canny 算法的检测时间仅相差0.427 s/张，本文算法仍满足实时性要求.

表1 算法检测时间对比

为了验证本文算法的正检率，从TILDA 标准织物图像库选取120 张织物疵点图像作为样本，其中正常、破洞、切口、油污、飞丝、断经（纬）各有20张.结果表明，算法正检率为95.83%，对比文献［16］中的算法提高了1.98%，相对优于文献［16］中的算法，满足疵点检测要求.疵点正检率对比如表2 所示.

表2 疵点正检率对比

3 结论

本文在经典Canny 边缘检测算法的基础上，提出一种自适应的Canny 边缘检测算法，在一定程度上保持了边缘的连续性，能很好地降低噪声，正检率也有所提高.小波模极大值算法对高频边缘信息进行定位，融合优化后的图像整合了高低频边缘的特征，使边缘更清晰、连续性和完整性更好，并能很好地消除噪声.但在对油污和断经（纬）类疵点检测时，与织物灰度值较近的疵点容易丢失，还需要进一步优化算法，融合时的加权因子α 该如何自动确定及边缘细化也还需要进一步的研究.