8 kW盘式永磁电机齿槽转矩分析与优化

2022-07-02邓秋玲廖宇琦艾文豪向全所朱明浩

湖南工程学院学报（自然科学版） 2022年2期

邓秋玲，廖宇琦，艾文豪，向全所，朱明浩

（湖南工程学院电气与信息工程学院，湘潭 411104）

0 引言

随着全球风电产业的高速发展，风电设备的需求量逐渐增大，发电机是风力发电系统中将风能转换为电能的重要装置.发电机不仅影响风电转换系统的性能和结构装置的复杂性，而且还影响输出电能的效率和质量.盘式永磁同步发电机与传统径向永磁同步发电机相比，具有功率密度高、体积小、结构紧凑等优点，得到国内外学者的广泛关注.虽然盘式永磁电机具有众多优点，但也存在一些问题值得研究.在风力发电系统中，永磁电机由于开槽电枢铁心与永磁体之间的相互作用会引起磁场能量的变化，从而产生齿槽转矩［1］.由于齿槽转矩的存在增大了起动时的阻力矩，并且运行时产生较大的噪声和振动，从而降低了风能的利用程度.故降低盘式风力发电机齿槽转矩，可以使得起动风速降低，从而有效提高风能的利用率，使盘式风力发电机在风速较低时便能发电.

有关永磁同步电机的齿槽转矩抑制方法，总的来说主要分成两类：一类主要通过电机控制策略来抵消，属于被动的抑制方法.而另一类为主动抑制方法，则从电机的本体结构来考虑，在设计电机本体时通过改变其结构参数来削弱电机的齿槽转矩［2］.文献［3］为了降低内置式永磁同步电机的齿槽转矩，提出了一种在转子侧开槽的设计方法，给出了12 槽10 极内置式永磁同步电机最佳开槽半径和角度.文献［4］对5 MW 的直驱永磁风力发电机的极弧系数和磁极偏移进行了研究，给出了齿槽转矩的最佳抑制效果.文献［5］提出了最优极弧系数的确定方法，通过修改转子的参数，使得电机的极弧系数趋于最优值，使得永磁电机的齿槽转矩得到降低.以上优化方法都是从单一参数来优化电机的齿槽转矩，尚未研究通过多维参数组合方式来降低电机的齿槽转矩.为了证明多维因素组合优化比单一参数优化降低齿槽转矩的效果更好，本文首先选取单个因素对齿槽转矩进行优化，再采取多维因素降低电机的齿槽转矩，最后进行对比分析，证明了多维因素降低齿槽转矩效果更具优势.

1 盘式永磁电机齿槽转矩数学模型

基于能量法的齿槽转矩定义是永磁电机定子绕组没有电流时，永磁体和定子槽之间相互吸引产生的转矩［6］.其定义为电机不通电时磁场能量W 相对转子位置角α 的负导数，即：

式中，α 为永磁体中心线与定子齿中心线的夹角，W 为电机内部的磁场能量.

为了便于研究，假设在同一电机中永磁体的形状一样，铁心的磁导率为无穷大，并且永磁体与空气有相同的磁导率.则电机内储存的磁场能量近似为永磁体中的磁场能量和电机气隙中磁场能量之和：

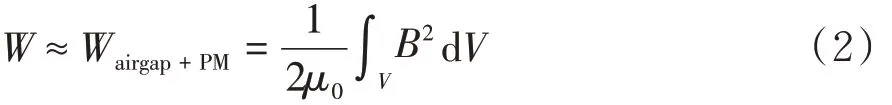
磁场能量W 由永磁体性能、定转子相对位置和电机结构尺寸决定，气隙磁密在电枢表面的分布可以近似表示为：

式中：δ（θ）为永磁体的有效气隙长度；hm（θ）为永磁体的充磁方向长度沿圆周方向的分布；Br（θ）为永磁体剩磁.

将式（3）代入式（2）可得：

式中，θs0为用弧度表示的电枢槽口宽度.

综合上式可得到齿槽转矩的表达式为：

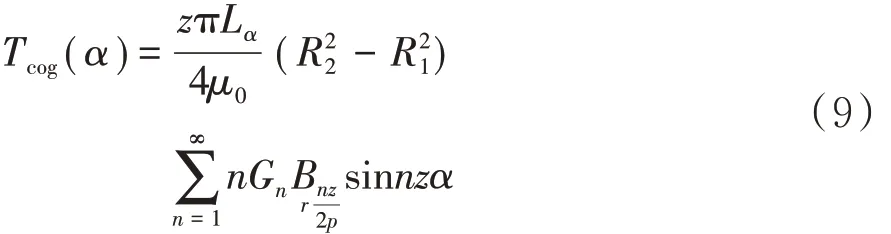
式中：μ0为真空磁导率；z 为电机定子槽数；Lα为电枢铁心轴向长度；R1为电枢外半径；R2为定子轭内半径；Br为永磁体的剩磁；n 为整数，n 的取值应该使nz/2p 为整数；p 为极数；z 为定子槽数；z 与极数 2p 的最小公倍数LCM（2p，z）.

2 盘式永磁电机齿槽转矩影响因素有限元分析

2.1 有限元模型的建立

以额定功率为8 kW、额定转速为3000 r/min 的3 相32 极48 槽盘式电机作为研究对象.其电机主要参数如表1 所示，建立电机有限元分析模型如图1所示.

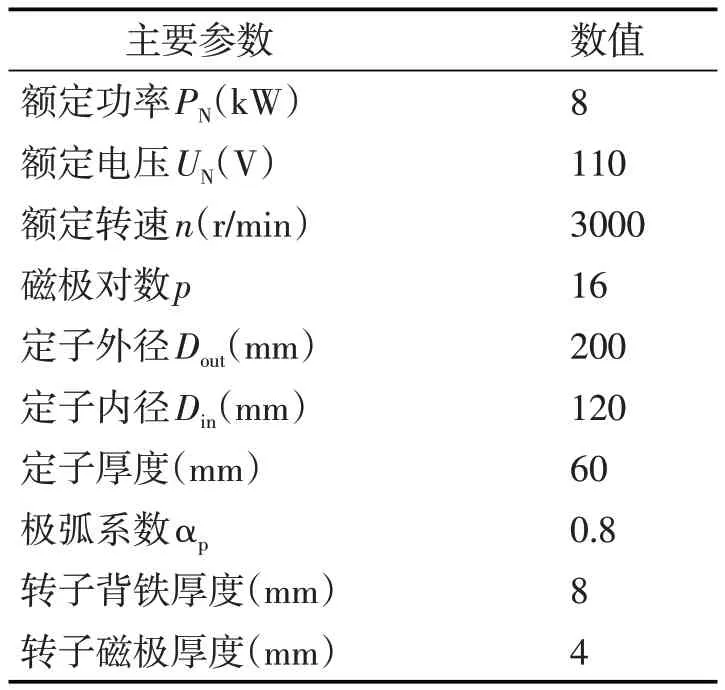
表1 电机主要参数

图1 盘式电机三维模型图

2.2 极弧系数对齿槽转矩的影响

电机的极弧系数αp是指电机极弧宽度与极距的比值.极弧系数的大小会影响气隙磁密的波形，同时也影响永磁电机的齿槽转矩.选择合适的极弧系数有利于减小电机的齿槽转矩.图2 为不同极弧系数下的齿槽转矩波形.由图可知，极弧系数为0.6时，齿槽转矩为8.03 N·m，极弧系数为0.9 时，齿槽转矩为11.28 N·m，极弧系数为0.75 时，齿槽转矩为0.875 N·m，本文选取的极弧系数为0.8 时，齿槽转矩为 4.9 N·m.相比极弧系数为 0.6 和 0.9 时，齿槽转矩降低了39%和56.8%.而当极弧系数为0.75 时，相比极弧系数为0.8 时降低了82%.故选择合理的极弧系数在一定程度上可以减少盘式电机的齿槽转矩.

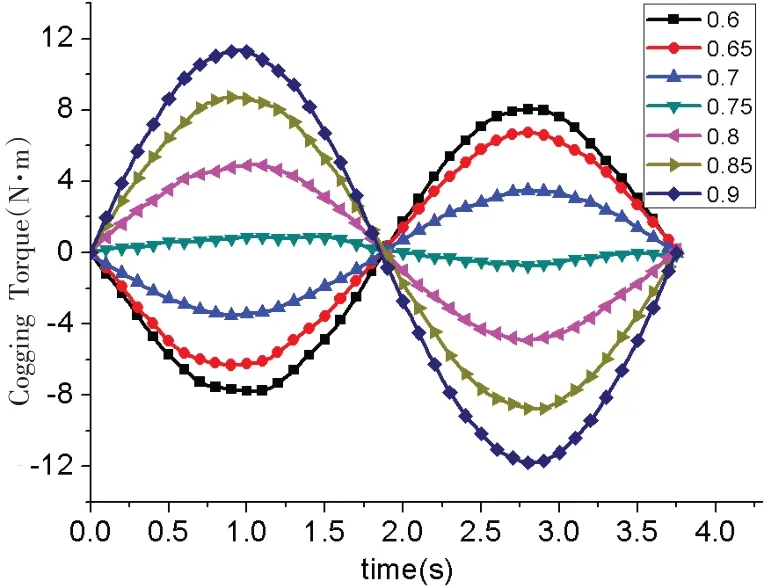
图2 不同极弧系数下的齿槽转矩

2.3 槽口宽度对齿槽转矩的影响

电机的齿槽转矩实际上是由转子的永磁体和电枢开槽相互作用产生的.定子槽开口会引起气隙磁导发生变化，定子槽口的大小会对齿槽转矩产生影响.选取槽口宽度分别为1 mm、2 mm、3 mm、4.5 mm，其中电机的槽口宽度为4.5 mm 时，电机为开口槽.从图3 中可以看出，开口槽电机齿槽转矩最大，其幅值为4.9 N·m.槽口宽度为1 mm 时，齿槽转矩最小，其幅值为1.61 N·m.相对于开口槽，槽口宽度为1 mm时，齿槽转矩降低了67%.由图可知，随着槽口宽度的增加，电机的齿槽转矩逐渐增加.因此，选取合理的槽口宽度有利于减小电机的齿槽转矩.但槽口宽度过小，对电机的加工制造要求有所提高.

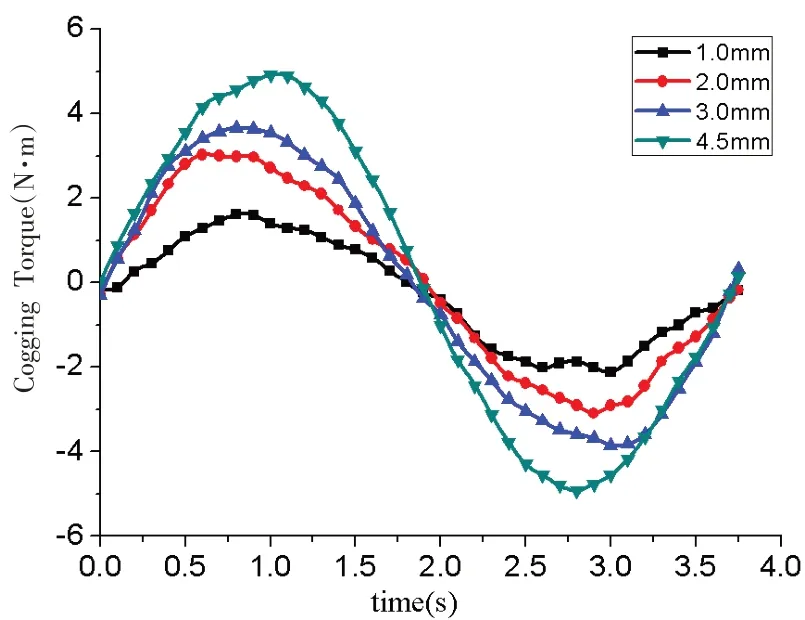
图3 不同槽口宽度下的齿槽转矩

2.4 磁极分段偏移对齿槽转矩的影响

转子斜极可以有效地减小永磁电机的齿槽转矩.对于传统永磁电机，转子斜极生产工艺有一定的难度，一般采用斜槽来削弱永磁电机的齿槽转矩.但是对于盘式永磁风力发电机，由于转子为平面形结构，转子斜极只需将永磁体在制作时倾斜一定的角度，使转子斜极生产工艺变得更简便.永磁体斜极分为两种：永磁体整体倾斜与永磁体分段倾斜.本文采用永磁体分段偏移来替代斜极.对于双转子盘式电机，可以采用单边分段偏移和双边分段偏移，又可以分两段及多段进行偏移.考虑到分段过多会使得制造成本提高，本文选取的永磁体均分为两段.图4 为永磁体分段偏移结构图，把永磁体均分为两段，在内半径处的永磁体不动，而将外半径处的永磁体旋转一个角度.

图4 永磁体分段偏移

对于双转子盘式永磁电机，当选取单边永磁体分段偏移时，不同偏移角度对齿槽转矩的影响如图5 所示，当永磁体的偏移角度为0.5°时，齿槽转矩为4.88 N·m，降低齿槽转矩的效果不明显，当永磁体的偏移角度为2°时，齿槽转矩为1.96 N·m，齿槽转矩降低了60%.从图中可以看出，随着磁极偏移角度的增加，齿槽转矩的幅值逐渐减小.

图5 单边不同偏移角度下的齿槽转矩

当选取双边永磁体分段偏移时，不同偏移角度对齿槽转矩的影响如图6 所示，当永磁体的偏移角度为0.5°时，齿槽转矩为4.87 N·m.齿槽转矩基本没有改变，并且还增加了工艺难度.当永磁体的偏移角度为2°时，齿槽转矩的幅值为1.47 N·m，齿槽转矩降低了70%.在偏移角度为2°时，双边永磁体分段偏移比单边永磁体分段偏移削弱齿槽转矩更加明显.

图6 双边不同偏移角度下的齿槽转矩

2.5 斜槽对齿槽转矩的影响

斜槽就是把电机齿槽沿轴向倾斜一定的角度，其中定子斜槽是削弱永磁同步电机齿槽转矩最有效的方法，斜槽可以削弱电机齿谐波引起的噪声和附加转矩.由于定子斜槽后导体沿轴向在磁场内的位置不同，具有一定的相位差，因此会削弱电机空载感应电压内的齿谐波电势.

图 7 为电机斜 0.2、0.4、0.6 和 0.8 个槽的齿槽转矩曲线图，当电机斜0.2 个槽时，齿槽转矩的峰值为3.14 N·m，当电机斜0.8 个槽时，齿槽转矩的峰值为1.3 N·m，相比未斜槽时，电机的齿槽转矩降低了35.9%和73.4%.从图中可以看出，随着斜槽个数的增加，电机的齿槽转矩削弱效果显著.

图7 不同斜槽下的齿槽转矩变化

3 基于田口法的齿槽转矩优化

3.1 正交试验设计方法

田口算法（Taguchi method，TM）作为一种新颖的全局优化方法，是由日本的知名统计学家与工程管理专家田口玄一博士在20 世纪50 年代提出的［6］.田口算法与一些现代优化算法和传统优化算法相比，因具有收敛速度快、试验次数少和鲁棒性强等优点而被广泛使用.正交试验是用一小部分试验来代替全部试验，是一种研究和处理多参数问题的高效试验设计方法.

对于电机的优化变量参数一般选取3～5 个值，水平影响因子为各个参数的取值范围，正交试验次数取决于优化变量参数的个数和水平因子数.设定永磁体四个变量参数：极弧系数为A、槽口宽度为B、永磁体偏移角度为C 和斜槽为D.通过4 个参数选取4 个水平影响因子来优化电机的齿槽转矩，根据电机的设计经验得出的优化参数水平值如表2所示.

表2 参数水平影响因子

3.2 正交表设计

根据上述选择，通过改变电机的极弧系数、槽口宽度、永磁体偏移角度和斜槽组合来降低齿槽转矩为目标.需要对4 个参数进行试验分析，并且每个参数有4 个水平因子，如果采用传统的优化方法，每次优化只改变一个变量，则需要44=256 次实验，而基于田口法的正交试验只需要4*4=16 次实验就可以实现对电机的多目标、多变量的仿真分析和设计.由于盘式风力发电机结构与传统电机不同，需要采用Maxwell3D 进行仿真分析，仿真时间长.采用田口法可以大大减少仿真所需要的时间，提高了计算的效率.表3 为正交试验表.