基于熵理论的铁路货物列车行车组织不确定性分析方法

靳 磊，司秀丹

(1.中国铁路信息科技集团有限公司 研发和建设处，北京 100844；2.北京全路通信信号研究设计院集团有限公司 通信信息院，北京 100070)

0 引言

铁路行车组织的基本要求是所有与列车运行有关的部门，必须按照列车运行图的要求，组织本部门工作以保证列车按运行图运行[1]。列车运行图以货物列车编组计划为基础，适当考虑货运量波动并结合现有线路通过能力，根据客货兼顾的原则综合平衡，合理确定货物列车编组对数。在此基础上，调度部门进一步结合运输生产实际，编制日(班)计划，作为调度日常生产组织的依据。各专业调度共同围绕日(班)计划，动态优化、合理调度完成行车组织工作。以上介绍反映了一种情况：尽管经过充分调研和科学编制，因存在众多影响行车组织工作的不确定因素，行车组织方案与运输生产实际必然存在偏差。

发现铁路行车组织中的不确定因素，消减或利用其影响一直以来是广大学者研究的热点领域。孙惠娟等[2]通过分析客运需求的不确定因素，研究了客运需求与开行方案互馈作用机理。刘笑佟等[3]研究了货运需求的不确定因素，提出需求预测模型与算法。袁志明等[4]分析了列车运行过程的不确定性并在算法中模拟了不确定性因素对模型的影响。严余松等[5-6]研究了货车车流、集结时间、改编作业存在波动性，利用随机模拟和模糊模拟等方法，建立了编组计划和车流径路综合优化模型。许可等[7-9]分析了编组站车流到达、接续及配流的统计分布规律，间接证明了编组站作业存在不确定性。石红国等[10]分析了集装箱需求和供给的不确定性并研究了不确定性因素对空箱调配作业的影响。廖志林等[11-12]分析了不确定信息对车流推算的影响，并采用提高数据采集频次和优化信息处理方法清筛无效数据。

有别于以上学者的研究内容和研究方法，在介绍行车组织不确定性的普遍性与必然性的基础上，研究如何从整体描述行车组织的不确定性并给出其定义与模型，最后结合业务分析模型的数学性质，以期为行车组织研究提供一种新的思路与方法。

1 铁路行车组织与不确定性

铁路行车组织的不确定性具有3 个特征：普遍性、必然性和递减性。其中普遍性可以通过众多学者关于行车组织的研究工作和研究成果得到间接证明，以下重点介绍必然性和递减性。

1.1 不确定性是铁路行车组织自身的必然结果

铁路行车组织以工作计划为主线，以分级管理为抓手，通过综合运用技术设备、合理组织列车运行完成各项运输任务。由于无法获得所有行车组织相关信息，实际一定不会完全符合计划。此外，实际生产过程中，计划落实、计划调整、计划外事项、不可控突发事件等均会进一步增加计划与实际的偏差。因此，铁路行车组织必然伴随着不确定性。

1.2 消减不确定性是铁路行车组织的重要内容

铁路行车组织是一个逐步将运输需求转化为日常工作方案，依据方案开展生产作业，并根据运输实际指导下一阶段工作的持续迭代过程。换个角度，根据该过程各环节的工作内容和工作成果，可将行车组织基本过程视为逐步消减其不确定性的过程。铁路行车组织基本过程如图1所示。

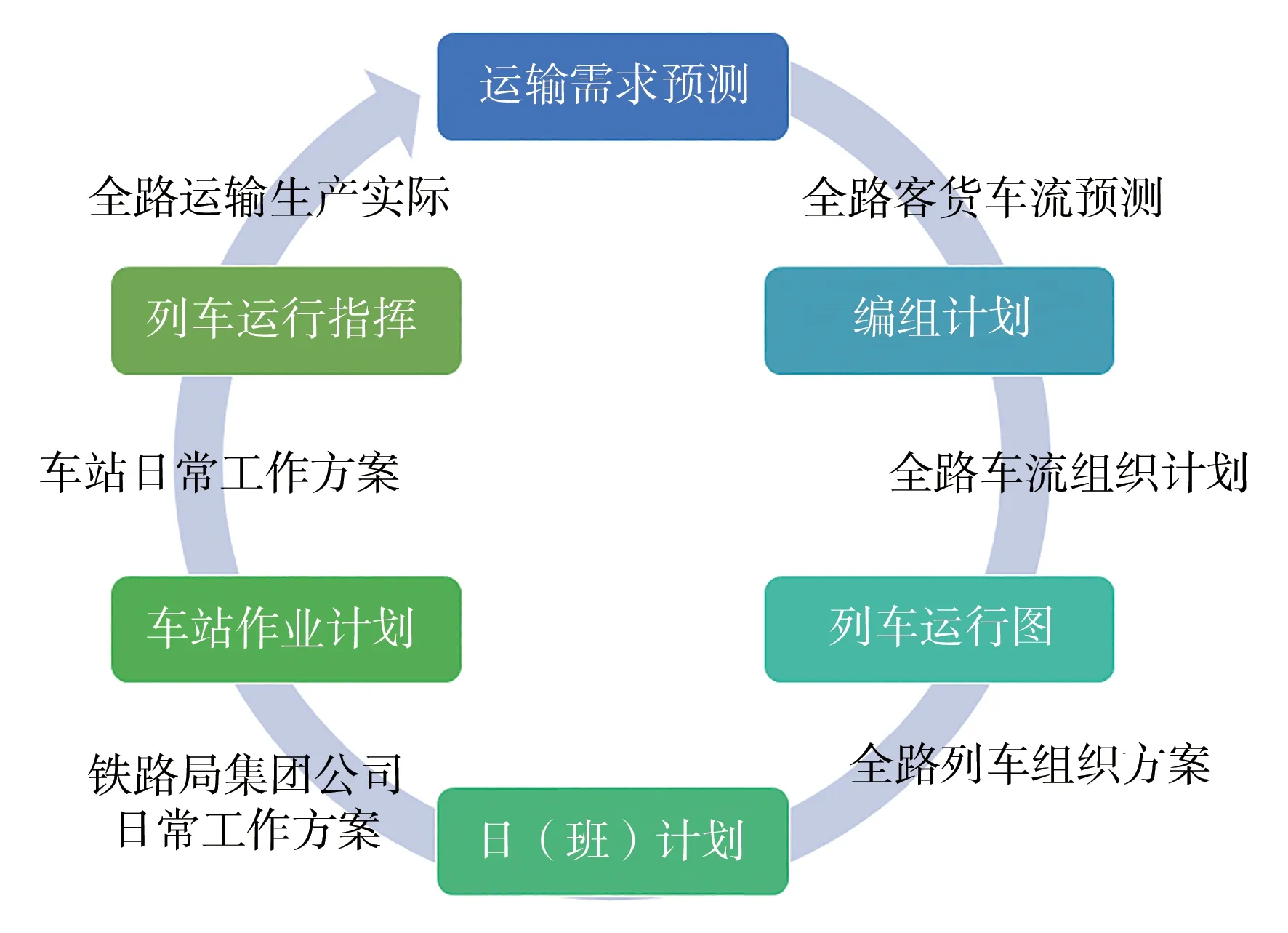
图1 铁路行车组织基本过程Fig.1 Basic process of railway operation organization

铁路客货运营部门基于年度或一定时期内全路客货运输需求，将需求转为车流，对该时期全路客货车流分布情况进行预测。运输部门基于车流预测，编制调整编组计划，将车流转为列车，提出列车的编组方案和开行方案，形成全路车流组织计划。进一步，运输部门组织全路运输专业部门，依据编组计划，组织编制列车运行图和机车周转图，明确列车时刻、列车对数、机车计划、施工计划及其他行车相关作业计划等内容。之后，调度部门依据列车运行图按级编制日(班)计划，形成行车、客运、货运、机车、车辆、动车、工务、电务、供电、施工等各级各专业调度共同参与编制执行的日常工作方案。其中，各车站进一步细化日(班)计划，编制形成车站作业计划，以具体落实日(班)计划要求。最后，调度部门协调组织各运输单位，围绕日(班)计划组织开展运输生产工作，并根据运输生产实际提出车流计划、编组计划和列车运行图调整建议。由此可见，随着行车组织工作的开展，各项工作计划不断分解细化，各个不确定因素一一转化为确定性因素，宏观运输需求最终分解为无数个目标清晰、内容明确、可执行、可度量的任务活动，这显然是一个不确定性持续消减的过程。

铁路行车组织不确定性的3 个特征反向映射了行车组织工作的基本过程和主要内容，为采用逆向思维，绕开确定性研究所遇到的困难，以不确定性为研究视角，探索铁路行车组织研究新思路和新方法奠定了基础。

2 铁路行车组织不确定性的定义

2.1 列车熵的定义

通常用“熵”来表示一个体系的不确定性，但熵的定义与模型往往与体系关注的主体密切相关，并不统一。例如，热力学关注系统的物理状态，用热力熵来度量系统的混乱程度；信息论关注信息，用信息熵来度量信息量的大小；生命学关注生命特性，用生物熵度量生命活动过程质量；经济学关注经济活动，用经济熵度量市场活力水平和企业多元化程度。考虑到行车组织基本过程主要围绕车辆与列车，并以列车完成运输任务的形式消减不确定性，因而研究将列车视为铁路行车组织的主体，借鉴以上体系定义熵的方法，研究提出用“列车熵”描述行车组织的不确定性。

列车熵定义为：统计意义下，车站(列车)关于待送车辆集结(运送)的不确定性的期望。其数学描述为：设车站(列车)ψ 待送车辆中，各目的站车辆数X1，X2，…，XM为一个矢量型随机变量，用(x1，x2，…，xM)或x 表示，服从p(x1，x2，…，xM)分布，车站(列车)列车熵T(ψ)的数学模型如公式(1)所示。

研究约定N 表示自然数，N={n|n ∈N}表示待送车辆辆数，M={m|m ∈N}表示待送车辆目的站个数，Xi={xi|xi∈N}表示待送到目的站i 的车辆辆数。为方便计算，log x 是以2 为底数的对数，底数没有特殊含义，可通过对数换底公式转换为其他底数。此外，研 究 约 定0·log 0=0，即 当p(x1，x2，…，xM)→0 时，p(x1，x2，…，xM)log p(x1，x2，…，xM)→0。列 车 熵 的 单 位用列车熵train entropy的首字母te表示。

按照列车熵的定义和数学模型，铁路行车组织基本过程可如下描述：铁路行车组织不确定性主要源于待送车辆(包括重车和待排空车)的不确定性，待送车辆的不确定性表现为某种概率分布；同一车站或区域待送车辆不确定性的汇聚表现为车流集结规律；根据车流集结规律，列车开行方案确定了列车类型、列车编组和列车径路，将车站的不确定性转移承接为列车的不确定性；列车以直达或接续运行方式将待送车辆送达目的站后完成运输任务，同时这些车辆相关的不确定性最终归零。可见，2 种描述方式基本契合，列车熵可以用于度量铁路行车组织的不确定性。

2.2 列车熵的数学性质

2.2.1 单目的站列车熵的数学性质

（1）M=0 时，表示车站不产生待送车辆或列车编组为空(出入段单机或救援单机等)。此时行车组织工作无作业或有明确的作业任务，组织方式简单，不会增加行车组织的不确定性，即列车熵TM=0=0。

（2）M=1时，公式(1)可退化为公式(2)。

TM=1应用于车站时，表示给定集结时间范围内，车站仅产生相同目的站待送车辆，并可用于度量该情况下该车站车流集结规律对行车组织不确定性的影响。

TM=1应用于列车时，表示列车中仅包含同一目的站的待送车辆。这类列车通常可视为以待送车辆目的站为终到站的点对点列车。此时，列车转移承接的待送车辆不确定性将随着列车的终到而归零，除计划外或突发事件外，各项工作均可按预先制定的方案开展，不会增加行车组织的不确定性，即列车熵TM=1=0。此外，给定集结时间范围内，相同目的站待送车辆辆数满足列车满轴条件且具有周期规律时，铁路部门将开行快运货物班列或始发直达列车。这类货物列车一般设置固定发到站、车次及运行线，并且有确定的开行周期、发到时刻和编组内容等要求，其组织工作清晰明了，不确定性极低或可忽略不计。

p(x)服从离散均匀分布时，列车熵TM=1(ψ)及其数学性质的函数图像如图2所示。

图2a 和图2b 表明p(x)服从离散均匀分布时，列车熵最大值与待送车辆集结不确定性成正比，图2c和图2d 表明列车熵最大值随着待送车辆辆数的增加而单调递增且增速渐缓，p(x)服从其他分布时，可采用同样方式分析列车熵的数学性质。

图2 列车熵TM=1(ψ)及其数学性质的函数图像Fig.2 Train entropy and function images of its mathematical properties

2.2.2 多目的站列车熵的数学性质

（1）列车联合熵。M ≥2 时，列车熵T(ψ)与多目的站待送车辆的联合分布p(x1，x2，…，xM)有关，此时列车熵又可称为列车联合熵。

TM≥2应用于车站时，表示车站产生2 个及其以上目的站的待送车辆。通过研究多目的站待送车辆的联合分布p(x1，x2，…，xM)，可进一步研究该类车站的车流集结规律对行车组织不确定性的影响。

TM≥2应用于列车时，表示列车待送车辆目的站不一致，列车终到后必然无法消除所有待送车辆的不确定性，还需要接续列车继续消减，因而TM≥2＞0。这类列车适用于在给定集结时间范围内，单一目的站待送车辆辆数不满足列车满轴条件时，将多个目的站待送车辆混合编组成列的情况。我国铁路货物列车多数采用混编方式，同时由于这类列车在集结、编组、运行线、运行时刻、解体等行车组织过程存在诸多不确定因素，它们也是构成全路行车组织不确定性的主要组成部分。

（2）线性可加性。M ≥2 且不同目的站待送车辆辆数Xi相互独立时，公式(1)退化为公式(3)，即不同目的站待送车辆辆数Xi相互独立时，列车熵可表示为各目的站待送车辆的列车熵分项的叠加，此时列车联合熵具有线性可加性。

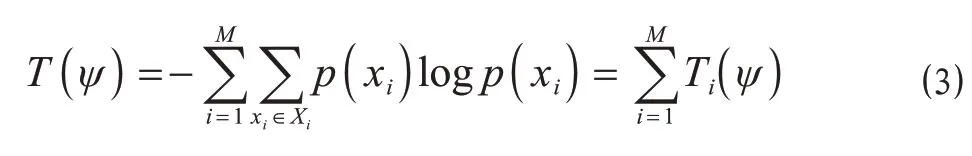
（3）列车条件熵。车站(列车)已包含目的站X 的待送车辆前提下，目的站Y 的待送车辆对车站(列车)不确定性的影响称为列车条件熵。设条件概率为p(y|x)，列车条件熵的数学模型如公式(4)所示。若X和Y 相互独立，则p(x，y)=p(x)p(y)，公式(5)表明此时列车条件熵为Y对列车联合熵的加成分项。

3 列车熵应用介绍

列车熵已应用于货物列车编组计划编制与执行评测等工作。

3.1 列车类型选择模型

选择合适的列车类型是编组计划的一项重要任务。运输部门细化提出了十几种列车类型，但如果以运输途中是否进行改编作业为标准，这些列车类型又可分为直达列车和接续列车2 大类。直达列车是指在始发站编组成列、途中无改编到达终到站的运输方式，其他途中需要改编的运输方式均为接续列车。通常情况下，若车站在一段时间内待送某站的车辆辆数、稳定性、紧迫性等方面符合一定要求，运输部门将选择开行直达列车，以最简单、最迅速的方式完成运输任务。但是，目前是否适合开行直达列车多采用经验判别法，缺少数学模型支撑，而列车熵兼顾了车站车辆集结规律、车辆辆数和列车编组满轴条件等内容，通过度量各种情况下行车组织的不确定性，可作为直达列车开行条件的定量分析模型。以下通过一个简化示例进行说明。

假设车站ψ 的列车熵T(ψ) =1，日均新增待送车站φ 车辆辆数C，即车站ψ 至车站φ 日增列车熵T+为C te；设直达列车满轴编组辆数M=50，且满轴方可开行，即每列车可消减车站ψ 至车站φ 的列车熵T-为50 te；当天未被运送的车辆，它们对应的列车熵TΔ将并入第二天新增的列车熵，并不断重复以上过程。根据上述假设，车站ψ 至车站φ 的待送车辆辆数分别为50，45，40，35 和25 时，车站ψ 至车站φ 的待送车辆辆数与列车熵的对应关系如表1 所示，车站ψ 至车站φ 的待送车辆辆数对应列车熵的技术指标如表2所示。

通过表1和表2可以获得以下信息。

（1）列车熵的消减过程具有周期性。周期性与待送车辆辆数C 和列车满轴编组辆数M 相关。例如表1中，C=45 时列车熵消减周期为10 d，C=40 时列车熵消减周期为5 d。

（2）列车熵消减周期相等时，周期内累计剩余列车熵总和相等，周期内日均剩余列车熵相等。例如表2，序号2，4，8，10 的消减周期均为10 d，周期内累计剩余列车熵总和为225 te，周期内日均剩余列车熵22.5 te/d；序号3，5，7，10 的消减周期为5 d，周期内累计剩余列车熵总和为100 te，周期内日均剩余列车熵20 te/d。

表1 车站ψ至车站φ的待送车辆辆数与列车熵的对应关系Tab.1 Corresponding relationship between the number of vehicles to be delivered from Station ψ to Station φ and train entropy

表2 车站ψ至车站φ的待送车辆辆数对应列车熵的技术指标Tab.2 Technical indexes of train entropy corresponding to the number of vehicles to be delivered from Station ψ to Station φ

（3）列车熵消减周期越短，周期内日均剩余列车熵越小。

（4）列车熵消减周期相等时，周期内日均消减列车熵与日均剩余列车熵之比表示列车熵能否得到有效消减，且该比值与日新增待送车辆辆数成正比。当日新增待送车辆辆数C ＜20 时，比值低于1，说明列车熵的消减速度低于新增速度，继续开行直达列车，行车组织整体不确定性将增加。

综合以上信息，周期内日均消减列车熵与日均剩余列车熵之比可作为判断是否开行直达列车的定量分析模型。通过设定阈值，待送车辆辆数超过阈值时建议开行直达列车，否则建议开行接续列车。如果附近几个车站相同到站的待送车辆均低于阈值，但是组合后能够超过阈值，则建议集中车辆后开行直达列车。采用该模型，可为每个车站或区域量身定制列车开行方案，避免“一刀切”的作业方式。

3.2 车站车辆集结与列车开行对数

列车熵可作为车站车辆集结与列车对数匹配性测算指标，为编制调整列车编组计划中的开行对数提供依据。以中国铁路北京局集团有限公司阳泉站为例，2020 年编组计划规定，阳泉站始发、解庄站终到直达列车每日开行0.5 列，每列编组重车50 辆。按照计划，阳泉站每2天应至少集结50辆目的站为解庄的待送车辆。根据2020 年6 月共30 d 运输信息，阳泉站日集结发往解庄的车辆数为33 辆的共1 d，35 辆的共26 d，36辆的共3 d。

以日集结辆数出现天数与总天数的比作为概率函数，2020 年6 月阳泉站以解庄站为目的站的车站列车熵为0.675，30 d总熵为709.425。每次列车可承接列车熵33.75，每2天开行1次，30 d共开行15次，可承接列车熵506.2，剩余待承接列车熵203.175，还需开行列车6.02 次。因此，按照以上测算结果，30 d 内应至少开行21次列车才能完成列车熵转移承接工作，即阳泉站至解庄站每天开行对数应调整为0.7。本次测算结果作为阳泉站编组计划调整建议，已被运输部门采纳。

3.3 列车编组内容兑现分析

列车编组计划规定了列车编组内容，编组内容包括待送车辆运输方向、牵引定数、车种类型、换长、欠补轴要求、关键任务等内容。运输部门需根据运输生产实际检查列车编组内容兑现情况，考核实际工作是否违流或编组内容是否需要调整。列车熵为兑现分析提供了算法：分别测算编组内容的列车熵T编与实际列车的列车熵T实，以T编为基线，分析给定时间范围内T实的符合情况；如果T实与T编基本符合，说明编组内容兑现情况较好；如果T实偶尔出现偏离T编的情况，说明存在违编的情况；如果T实整体偏离T编，说明编组内容与实际运输情况出现偏差，需要进行调整。该算法已应用于货物列车编组计划编制与执行评测工作中。

3.4 列车径路选择方法

列车从始发站到终到站可选择多条径路，传统径路选择方法包括计费径路、运行径路和时效径路等。由于传统径路选择方法缺少可比较的共同指标，无法评估不同类型径路选择结果对路网能力的影响，而测算径路列车熵可以作为共同指标，为开展这类评估工作提供支持。径路列车熵可由所有经由该径路的列车所承载列车熵的总和表示。径路列车熵总和大的，经由该径路的列车多，反之列车少。若考虑均衡运输原则，列车应选择列车熵较小的径路。若列车的列车熵较大，表示其编组包含不同目的站车辆较多，应选择终到站为技术站的径路，将分散不确定性汇聚，以便重新分配承载列车，尽早归零列车熵。若列车的列车熵较小，表示其编组包含不同目的站车辆较少，应选择终到站为主要车辆目的站的径路，以尽快实现列车熵归零。

3.5 列车编组计划与调度日(班)计划质量测算

货物列车编组计划的列车熵可通过计算所有车站列车熵总和或列车列车熵总和获得。编组计划调整后，可计算调整前后编组计划列车熵的改变情况，辅助支持调整效果分析与评估。同理，调度日(班)计划也可采用此方法，开展定量分析，为评价日(班)计划编制质量提供支持。进一步，可开展编组计划与日(班)计划对比分析，评测日(班)计划兑现情况，评估编组计划符合性。

4 结束语

从铁路货物列车行车组织工作不确定性入手，分析了不确定性的普遍性和必然性，提出以不确定性为视角描述行车组织工作，并将行车组织不确定性定义为列车熵。列车熵的核心是发现车流集结规律、列车类型、列车编组、列车径路等行车组织过程不确定性的内在联系，建立可统一度量行车组织各项工作的数学模型。基于列车熵定义及其良好的数学性质，研究介绍了列车熵在货物列车编组计划编制与执行评测方面的应用成果，并提出进一步研究推广建议，以期为行车组织研究提供新思路与新方法。