四支点压电测力仪输出稳定性提高方法研究

张 军，马奕萱，任宗金，刘禹廷，甄田甜，仲育颉

(大连理工大学机械工程学院，辽宁大连 116024)

0 引言

在机械加工领域，如复合材料、铝合金、钛合金加工中，通常用测力仪监测切削力的方式对切削过程进行监控，以便控制切削过程[1-2]。四支点压电式测力仪以其量程大、通用性广等优点得到了广泛应用[3-5]。在实际加工中，测力仪通过感应装夹在其上表面的工件的受力情况实现力测试。但由于各类工件的结构和尺寸不同，导致每次装夹的位置不固定，故要求测力仪在不同测试位置均保持良好的测试准确性，即测力仪在不同测试位置所对应的输出差异量较小。对此，王志军[6]、宋鹏[7]和齐亚洲[8]等分别提出了映射矩阵法、联立标定法和输出比例归一化法，用以补偿不同测试位置的测试误差。这些方法提高了测试精度，但都采用的是数值后处理的方式，未考虑各传感器的性能差异对于降低不同位置测试误差的影响。

本文从传感器的性能差异出发，构建起各传感器输出电压在不同位置的差异量的解析式，进一步确定了传感器优化布置次序，降低了测力仪对力源位置的敏感度。同时，在确保4个传感器高度、刚度和装配精度差异均满足要求的前提下，以测力仪的法向标定为例，进行了传感器优化次序布置前后对比实验，并计算了不同加载位置的输出电压差异量。

1 四支点测力仪输出电压差异量分析

四支点测力仪的主要构件包括上板、下板以及4个传感器，其基本结构与力学分析模型如图1所示。为便于分析和表达，定义4个传感器的布置跨距为2a×2b，定义矢量力作用位置的坐标为(δx，δy)，将4个传感器从a～d依次进行编号，并把4个布置位置依次编号为1～4号。

(a)四支点测力仪结构

在进行力测试时，被测矢量力可沿三坐标轴分解为3个力分量，根据力分配原理逐一分解到4个传感器，由传感器内部不同切型的石英晶片感应并输出相应电压值。基于力矩平衡和杠杆原理，在前期的工作中推导了在测力仪具备足够刚度的情况下4个传感器的力分配关系解析式，详见文献[9]。基于理论力学相关知识，可知测力仪的各向受力与4个布置位置的传感器在对应方向所受的分力之和相等，即：

(1)

式中：j为X、Y、Z3个方向；i为第i号布置位置的传感器，i=1,2,3,4；Fj为测力仪在j方向的受力；Fji为第i号布置位置的传感器在j方向所受的分力。

将第i号布置位置的传感器的力电转换系数用符号ki表示，则X、Y、Z三个方向的力电转换系数平均值如式(2)所示：

(2)

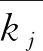
以j方向力电转换系数的平均值为参考，传感器在该方向的力电转换系数的实际值与平均值的差值则代表该传感器力电转换系数的偏离程度，称为离差。而且，4个布置位置的传感器力电转换系数的离差之和为零，如式(3)所示：

(3)

式中：Δkji为第i号布置位置的传感器在j方向的力电转换系数的离差。

引入力电转换系数离差的标准差σk，标准差的计算方法如式(4)所示。

(4)

力电转换系数离差的标准差代表了4个布置位置的传感器的力电转换系数的接近程度。当标准差数值越大时，表示4个布置位置的传感器的力电转换系数的差异越大，会导致测力仪在不同测试位置的输出电压差异量越大。由传感器的力电转换系数差异所导致的三向输出电压的差异量可表示为：

(5)

式中ΔUj为测力仪在j方向的输出电压差异量。

将式(1)～式(5)代入传感器力分配关系解析式，可得到三向输出电压差异量如式(6)所示。

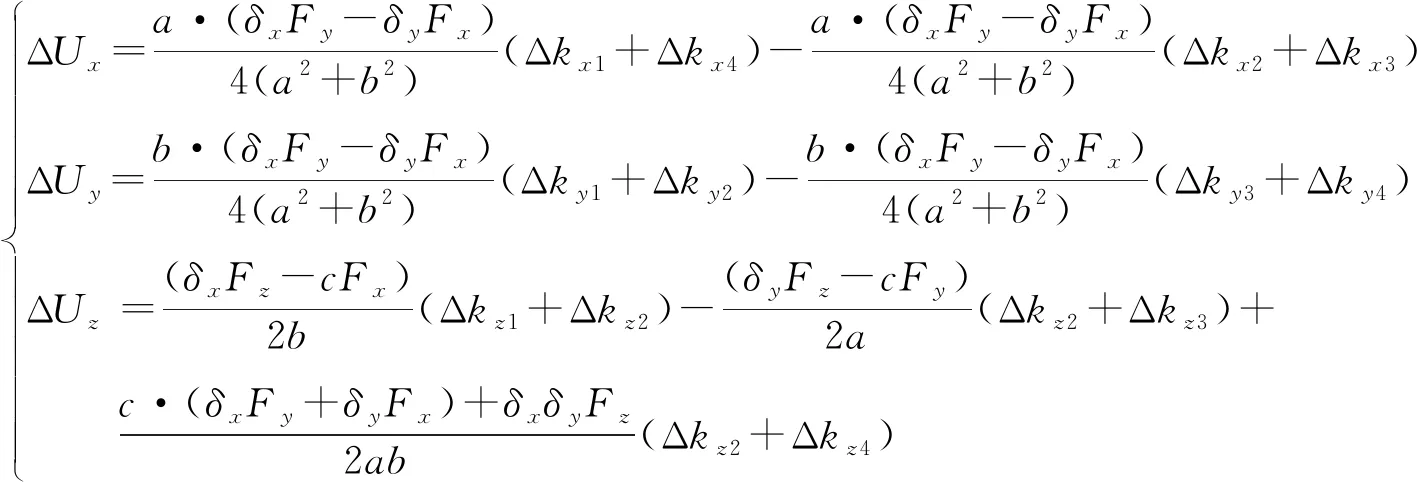
ΔUx=a·(δxFy-δyFx)4(a2+b2)(Δkx1+Δkx4)-a·(δxFy-δyFx)4(a2+b2)(Δkx2+Δkx3)ΔUy=b·(δxFy-δyFx)4(a2+b2)(Δky1+Δky2)-b·(δxFy-δyFx)4(a2+b2)(Δky3+Δky4)ΔUz=(δxFz-cFx)2b(Δkz1+Δkz2)-(δyFz-cFy)2a(Δkz2+Δkz3)+c·(δxFy+δyFx)+δxδyFz2ab(Δkz2+Δkz4)

(6)

式中：δx、δy分别为矢量力作用位置在X、Y方向的坐标；Fx、Fy及Fz分别为测力仪在X、Y及Z方向所受的力值；a与b为测力仪中4个传感器跨距的1/2；c为测试位置到传感器中心平面的法向距离。

观察式(6)可知，三向输出电压差异量的大小主要与力电转换系数离差、传感器布置跨距、测试点的位置以及被测力分量有关。因此，在确定测力仪结构和测试工况的情况下，为降低测力仪对不同测试位置的敏感度，可以根据各传感器的力电转换系数离差值调整其布置次序以减少输出电压差异量。

2 传感器布置次序及影响因素

2.1 传感器优化布置方案

根据式(6)所示的输出电压差异量的解析式，就X向而言，为使该方向的输出电压差异量尽可能小，则应使1号和4号，以及2号和3号布置位置安装的传感器的力电转换系数离差数值接近相反数，从而相互抵消。同理可对Y向和Z向进行分析，得到各布置位置的三向力电转换系数离差的约束条件如式(7)所示：

(7)

通过标定装置分别测定4个传感器的力电转换系数。选用量程为3 000 N的标准力传感器，分别对传感器的X、Y和Z向施加阶梯力载荷，在上位机软件观察并记录输出电压。输入载荷与输出电压的比值即为力电转换系数，实验结果如表1所示。

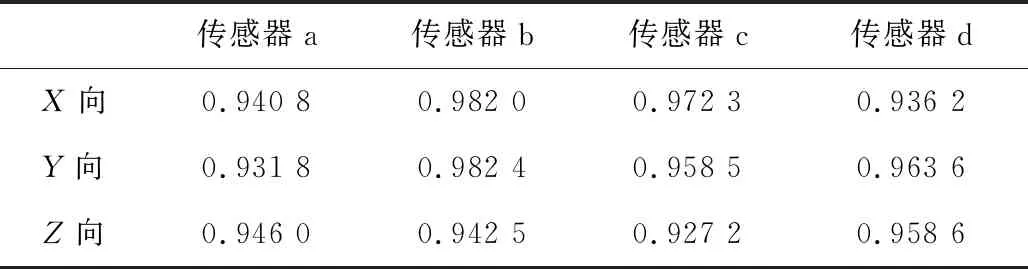
表1 传感器的力电转换系数 N/mV

根据表1中数据计算各向力电转换系数均值，通过计算力电转换系数的实际值与该向均值的差值得到力电转换系数离差，结果如表2所示。

表2 传感器力电转换系数离差 N/mV

结合式(7)所示的力电转换系数离差约束条件，最终确定出4个传感器的布置次序位置为：传感器a布置在1号位置，传感器d布置在2号位置，传感器c布置在3号位置，传感器b布置在4号位置。

2.2 排除影响因素

传感器参数差异主要包括高度、刚度、装配精度、力电转换系数差异等，这些差异性都会不同程度地影响测力仪对力源位置的敏感度。本文主要研究传感器性能差异对于力源位置敏感度的影响，因此为使得实验结果更具可靠性，在实验之前首先应确保传感器的其他参量均满足测试要求。

2.2.1 传感器高度差异

采用量程为50～75 mm的数显千分表分别测量4个传感器的高度。将传感器放置在高精度测试平台上，为保证测试结果的准确性，分别选取4个不同的位置进行测量，并在每个位置重复测量3次，再将测量结果取平均值，得到4个传感器的高度及差异量如表3所示。

表3 传感器高度 μm

由表3可知，4个传感器的最大高度差异为6 μm，小于高度允差值30 μm，满足测试要求。

2.2.2 传感器刚度差异

为测量传感器的刚度，将传感器安装在标定加载台上，通过标准力传感器分别对传感器的X、Y和Z向施加3 000 N的载荷，由电感测微仪测量出传感器在受力方向所产生的变形量，如表4所示。

表4 传感器变形量 μm

根据施加的载荷和对应的变形量计算得到测力单元的刚度，结果如表5所示。

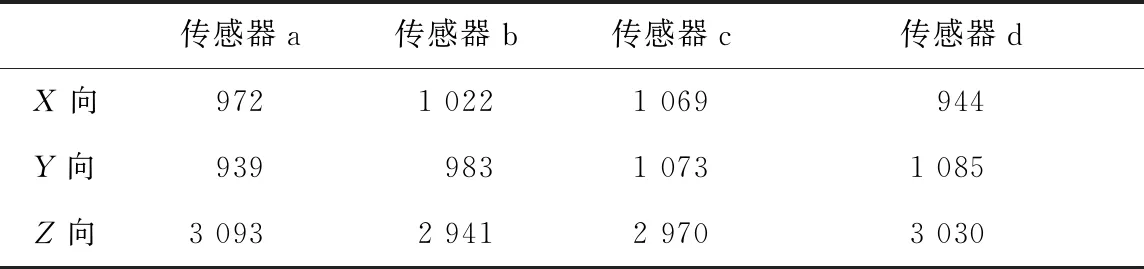
表5 传感器刚度 N/μm

由表5可知，4个传感器的切向刚度均接近1 000N，法向刚度接近3 000N，各向刚度差异均小于±100N/μm，满足测试要求。

2.2.3 传感器装配精度差异

传感器装配误差主要包括装配偏角误差和装配位移误差。将传感器放置在高精度测试平台上，通过精度为0.01mm的数显深度尺分别测量装配偏角误差和装配位移误差。得到装配位移及偏角测量结果如表6所示。

表6 传感器装配精度

表6中：Δx为传感器在X方向的装配位移误差；Δy为Y方向的装配位移误差；θ为装配偏角误差。

由表6可知，4个传感器的最大装配偏角误差为0.52°，小于装配偏角允差1.70°[10]；装配位移误差为0.37 mm，小于切向装配位移允差0.38 mm，满足测试要求。

3 实验与分析

实验装置主要由加载装置、电荷放大器、数据采集卡、计算机和Dewesoft 6标定软件组成，如图2所示。为了使输出电压与力值匹配，将X、Y向的电荷灵敏度系数设为8.00 pC/N,将Z向的电荷灵敏度系数设为4.00 pC/N。

图2 实验设备及标定流程

实验分为两部分，首先将4个传感器随机布置进行标定实验，然后按照优化次序布置方案进行布置与组装的测力仪进行对比实验。选取标定板上表面的13个位置作为测试点，并选用5 000 N量程范围的标准力传感器进行加载。如图3所示。

图3 标定实验示意图

为保证实验结果的准确性和可重复性，每个加载点重复加载3次，得到优化布置前后的各加载位置输出电压对比图如图4所示。

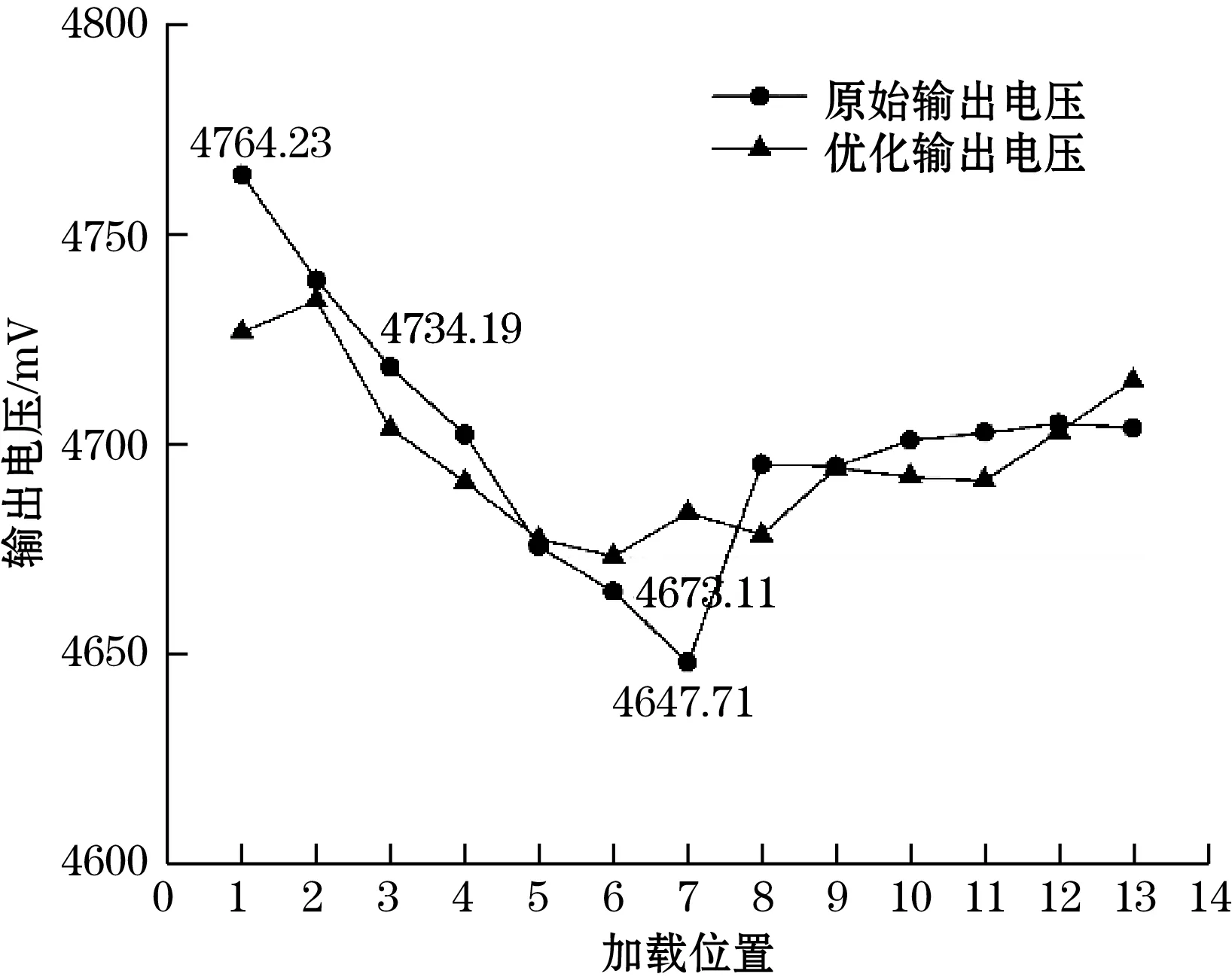
图4 Z向优化布置前后差异量对比

由图4可知，在13个标定位置中，采用传感器随机布置的测力仪输出电压最小值为4 647.71 mV，最大值为4 764.23 mV，计算可知差异量为116.52 mV；按照传感器优化布置次序进行组装的测力仪输出电压最小值为4 673.11 mV，最大值为4 734.19 mV，差异量降低至61.08 mV。因此，得到优化布置前后测力仪输出电压差异量减少了约48%，验证了优化布置方法的有效性，大大降低了测力仪对于力源位置的敏感度。

4 结论

本文从测力仪的矢量力测试原理出发，针对测力仪在不同测试位置对应的输出电压不一致的问题，分析了传感器力电转换系数差异对输出差异量的影响。三向输出电压差异量的大小主要与传感器力电转换系数、传感器布置跨距、测试点的位置以及被测力分量有关，本文主要探究了各布置位置所安装的传感器的各向力电转换系数差异性要求，并进一步提出了四支点测力仪的优化次序布置方法。在实验中，按照最优布置方案组装测力仪，忽略测力仪在测试过程中的整体变形，在排除其他干扰因素的前提下进行了法向标定实验。结果表明：优化布置前后测力仪的输出差异量从116.52 mV降低至61.08 mV，输出差异量减少了48%，提高了四点支撑测力仪面域内变加载点电压输出的数值稳定性和标定精度。