改进图论法在河湖水系连通规划中的应用研究
2022-07-02张琼海
姜 宇,张琼海,严 萌
(1.珠江水利委员会珠江水利科学研究院,广东 广州 510610;2.珠科院工程勘察设计有限公司,广东 广州 510610)
近年来,随着珠江三角洲地区经济的快速发展,人口密集程度增加,生活污水的排放也随之增加,河网的水资源与水环境承载能力已经渐显不足,加强河湖水系连通,增强河道水动力,提升水体交换速率,能有效缓解该问题[1]。在开展河湖水系连通规划前,通过定量评价河湖水系连通性,能够更加有效指导并优化连通方案。目前河湖水系连通性评价主要有图论法[2]、网络分析法[3-4]、指标法[5]、水文模型分析法[6]、景观生态学法[7]等方法,其中基于图论或改进的图论方法评价较多。徐光来等[8]提出了以河道水流阻力和图论方法相结合的河网加权连通性定量评价方法,并对太湖流域嘉兴平原河网进行了评价。赵进勇等[9]利用图论理论,采用边连通度参数定量评价胶东地区水网的水系连通性。孟慧芳等[10]建立基于水流阻力与水文过程的平原河流连通评价方法,对比其他连通性评价方法结果更符合实际。陈星等[11]基于图论,采用水流流通度,构建权值邻接矩阵,实现对河网的水力连通度的定量评价。高玉琴等[12]基于改进的图论法,以反映流域水量指标的连通因子为权值,构建水系连通度定量评价模型,计算河网加权连通度,定量评价河网水系连通性。以上研究多数基于图论或改进方法计算分析水系自身的连通性,较少开展定量分析水系连通性并指导水系连通规划研究。
本研究以珠三角感潮河网为对象,针对其水流受径流和潮汐流双重影响,流态呈现往复流,导致河网内污染物来回震荡的问题,利用图论分析法中可考虑边的方向,能够反映单向流、双向流的优势,考虑水流阻力对水力连通的影响,计算不同河网连通方案下的最小阻力,选取最优方案,并结合数学模型加以细化,为感潮河网水系连通性诊断和规划提供依据。
1 研究方法
图论是组合数学的一个分支,图论中的图包括2个要素:对象及对象中的二元关系。在河湖水系连通中,将不同水体作为对象用点表示,将各对象之间是否连通作为对象间的二元关系,用边来表示[13]。如此一来,便能将图论应用于河湖水系连通的复杂连通网络分析。
1.1 图的邻接矩阵构建
图由边和顶点组成,对于一个确定的图,顶点与顶点之间、顶点与边之间的关联关系也唯一确定。而数学计算中常用的矩阵,恰好适合用来描述图模型中顶点与顶点、顶点与边之间的结构关系,并且矩阵的形式便于作为计算机输入,当图模型的拓扑结构具有极高的复杂度的时候可以借助计算机的运算能力,对图模型进行复杂网络分析与优化。即对图模型相应的矩阵表示作深入研究,可以得出图所具有的一些潜在特性[8-9]。邻接矩阵表示点与点之间的邻接关系。一个n阶图G的邻接矩阵A=(aij)n×n,见式(1)。
(1)
对于图1a,其邻接矩阵A见式(2);对于图1b,其邻接矩阵B是一个对称矩阵,见式(2)。
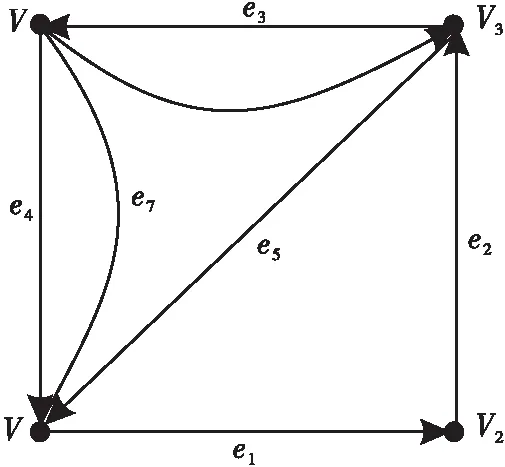
a)有向图
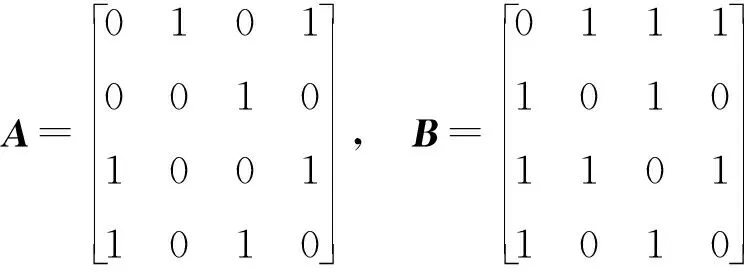
(2)
1.2 “最短路”思想与计算方法
最短路问题是图论研究中的一个经典算法问题,经常用于解决人们生产实际中的一些优化问题,如运输路径与成本、地点的选址和布局等。将图模型中的边赋予一定的含义并给予数量权值,如路径长度,找出图模型两节点之间总权和最小的路径就是最短路问题[14];设图G=(V,E),顶点集记作V={v1,v2,…,vn},G的每条边赋有一个权值,Wij表示边vivj上的权,若vi、vj不相邻,则令Wij=+∞。引入国内学者提出的水流阻力的概念与计算方法,结合图论中的“最短路”思想,将顶点间水流阻力作为权值,将最短路问题转化为最小阻力问题;利用式(3)—(5)所述方法计算各个河段的阻力,得到加权邻接矩阵,并通过MATLAB计算出2个节点之间的最小阻力与其对应的路径。具体计算流程见图2。
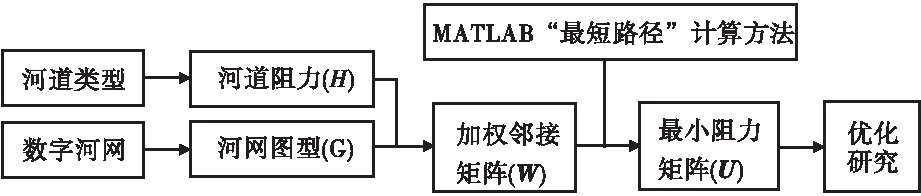
图2 最小阻力计算流程
1.3 河道阻力计算
对于独立开放河道,河道流量与河道坡度、纵坡面形状和河道糙率有关[15]。流速可用曼宁公式表述:
(3)
式中V——截面平均流速;n——曼宁糙率系数;R——河道水力半径;Sf——摩阻坡度。
在稳定流条件下,Sf可用河床坡度表示[52],由于研究区域处于珠江三角洲平原河网,河床坡度较小,可忽略不计,由此可得到以下关系:
(4)
水力半径R等于河道纵切面积除以湿周,并且由于水流运动的过程中,会因摩擦力的作用而损失能量,造成流速降低,因此综合考虑糙率n、输水距离L,最终得到两相邻节点间的水流阻力计算公式:
H=LnR-2/3
(5)
2 研究区域概况
中顺大围地处珠江三角洲网河区下游,地势西北高,东南低,区内河网密布,水系纵横交错。中顺大围的西面为古镇水道、西海水道及磨刀门水道,北面为东海水道,东面为横门水道,其中的横门水道及磨刀门水道为珠江八大口的其中2个,主要承泄西江洪水。境内河网密度较大,河段间相互交织,河涌干支流及人工排洪渠等合计298条,围内最主要的2条骨干河涌——岐江河和凫洲河至狮滘河段横贯中部,为中山市主城区的主要河流,合计约80 km。中顺大围联围后主要河涌近100条,总长超过500 km,骨干河涌为岐江河、凫洲河、西部排水渠和赤洲河。骨干河涌从分布上基本形成了“三横、三纵”互通,汇入岐江河的格局。具体水系分布格局见图3。中顺大围境内的水利工程设施主要包括堤防与闸泵两大类型。中顺大围联围堤防总长度约为119 km,包括东干堤53 km,西干堤66 km,其中中山段89 km,顺德段30 km。沿堤共有47座水闸,顺德15座,中山32座。其中有2座大型水闸、4座中型水闸,其余41座为小型水闸。中顺大围工程管理处的直属工程有4个,分别是东河水利枢纽工程、西河水闸、铺锦水闸及拱北水闸。
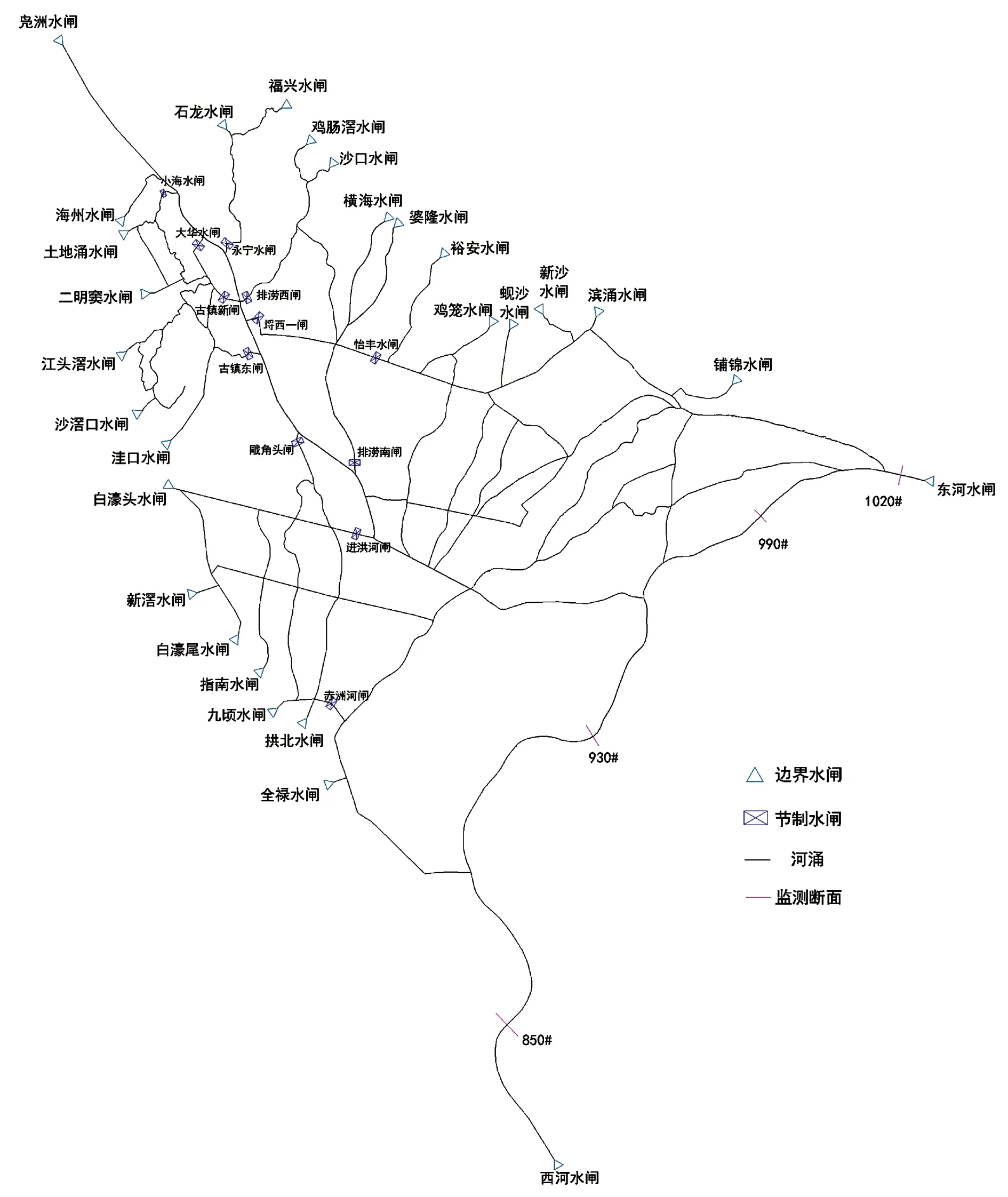
图3 研究区域水系分布
3 连通度计算及分析
建立中顺大围一维水量—水质耦合模型与图论“最小阻力”分析工具,利用图论“最小阻力”分析工具对中顺大围图模型进行计算分析,确定方案,并利用一维模型的计算结果进行相互比对、验证,用于优化中顺大围的连通方案。并对各个连通方案的总引进水量、水体更新速率、断面污染物浓度合计进行统计,作为比较依据。
3.1 邻接矩阵构建
根据图3,结合图1介绍,形成图论计算所用图模型,对河网中的节点进行编号,共有108个节点,140条边。根据式(2)得到式(6)所示邻接矩阵。
(6)
注:因矩阵为108×108矩阵,由于篇幅原因,只展示部分,下同。
3.2 基于水流阻力的加权邻接矩阵构建
根据河道的断面信息及相应工况下的水位边界,通过MATLAB计算各个断面的水力半径R,其中一个河段的水力半径用其包含的所有断面的水力半径的平均值表示,并采用式(5)计算各个河段的阻力,最小阻力值H作为各河段权重参数,仅反映相关河道对水流阻力的相对关系,本次研究以无量纲量处理。若是两点间直接通过一条边相连,则两点间的水流阻力为两点间河段的水流阻力;若两点间有多条边相连,两点间的水流阻力取所有河段中最小的水流阻力;若两点间无边直接相连,则两点间的水流阻力为无穷大,在邻接矩阵中记为inf[16]。本次研究处于平原感潮河网,忽略河底比降,所得的邻接矩阵为对称矩阵。图4所示,将河道汇合点、边界条件和闸坝堰看成图的顶点(V1,V2,V3,V4),河道看成悬挂边(e1)、边(e2,e4)或多重边(e3,e5),建立河网图模型G。用邻接矩阵W=(wij)n×n表示河网图G,wij是顶点Vi和Vj之间的水流阻力,W为对称矩阵。设H1、H2、H3、H4、H5为对应河段的水流阻力。由于感潮河网区的河底坡降很小,因此本次研究中忽略坡度的影响。通过计算得到中顺大围图模型的加权邻接矩阵见式(7)。
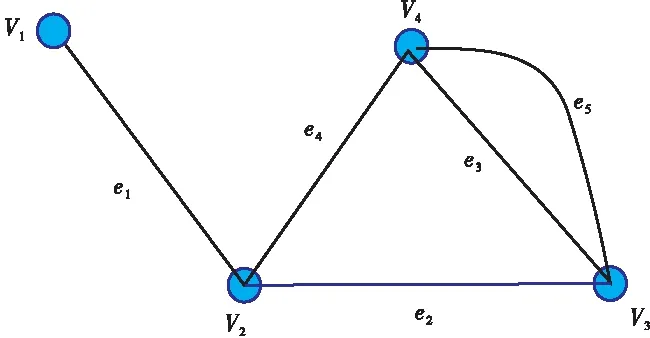
图4 加权邻接矩阵构建示例
(7)
4 成果分析
4.1 基于图论的连通方案优化
a)西河水闸为研究范围内最大的引水闸,因此以西河水闸为起点,寻找最小阻力出水路径。由表1可以看出,西河水闸至东河水闸阻力值最小,为192.36,其次为至铺锦水闸阻力,为224.64。通过对中顺大围各外江水闸的规模、排水能力做分析,并结合计算结果,初步拟定方案1,即将铺锦水闸、东河水闸作为定向排水闸,其余外江水闸均定向引水,各内部节制闸定向引、排水,使围内水体总体由西向东、由北向南流动。
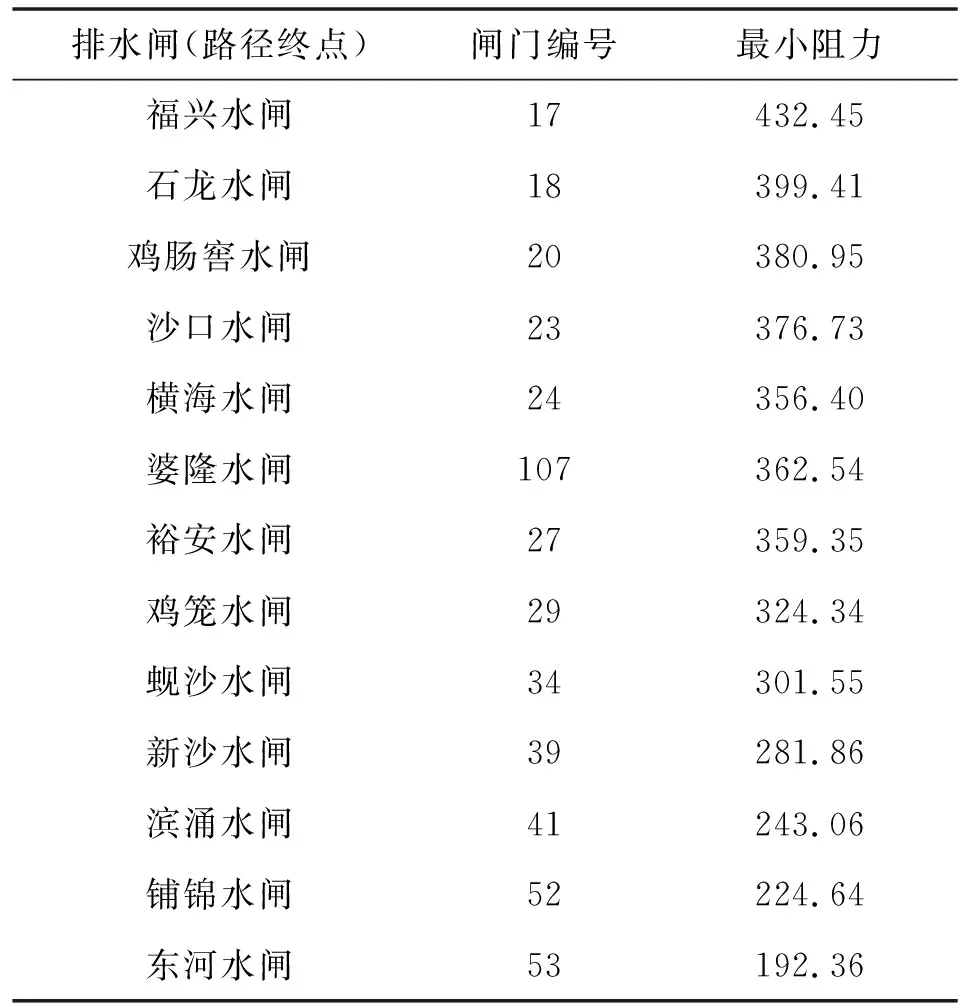
表1 西河水闸为起点的最小阻力路径分析成果
b)进一步对其余外江水闸到铺锦、东河水闸之间的最小阻力分析(表2),结果显示,其余26个外江水闸到铺锦水闸的最小阻力平均值为260.25,到东河水闸的最小阻力平均值为257.45,整体平均值为258.85。而经计算得铺锦水闸到东河水闸的最小阻力为58.98,若将铺锦水闸也作为引水闸,则连同表2中的26个外江闸,到东河水闸的最小阻力的平均值为250.10,比同时将铺锦、东河水闸作为排水闸时的阻力要小,据此拟定连通方案2:圩内各节制闸定向引、排水,东河水闸定向排水,其余外江水闸定向引水。
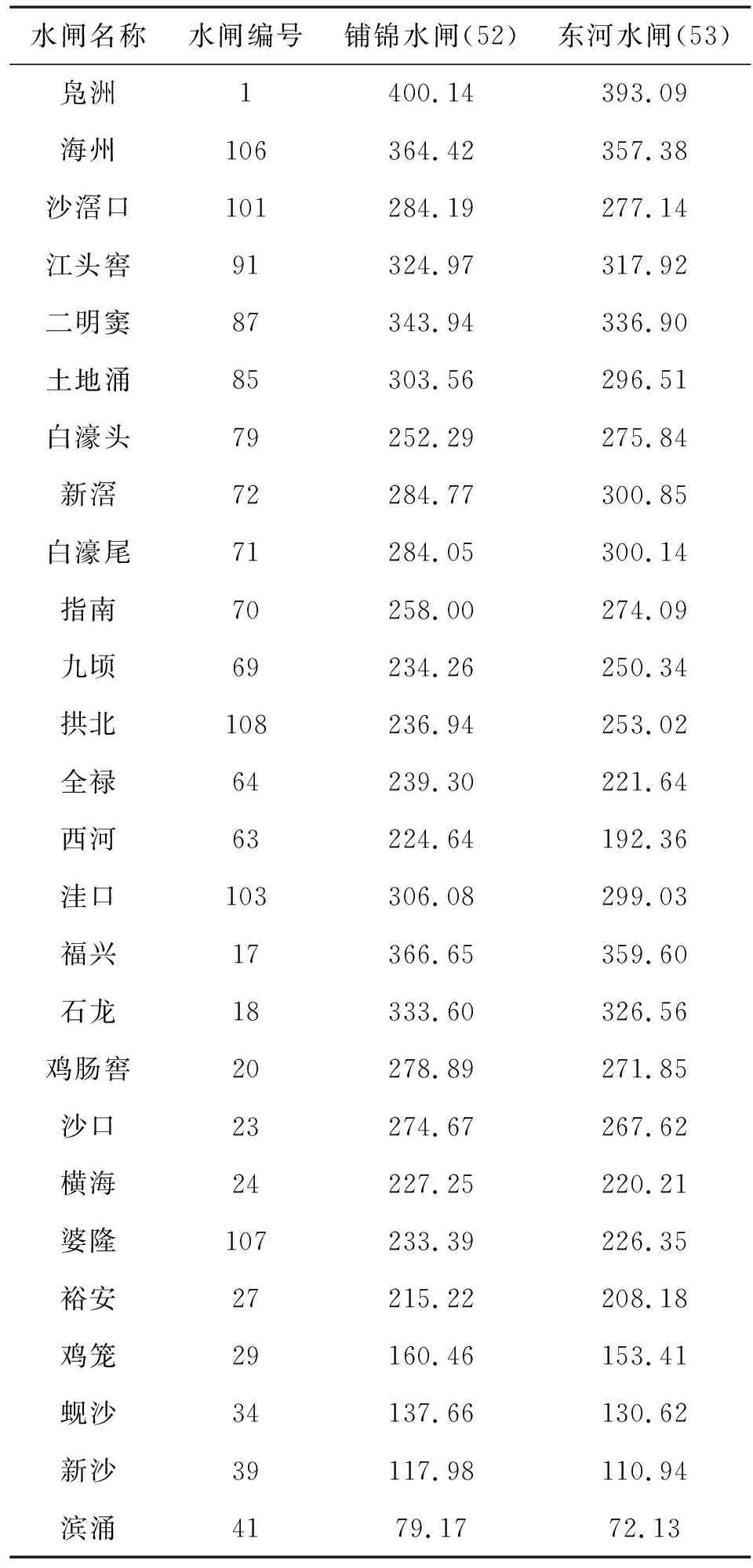
表2 其余外江水闸到铺锦、东河水闸之间的最小阻力分析
c)考虑结构连通性方面,使连通时间保证率提高,同时为了节省调度成本,将12个节制闸全部打开,维持东河水闸定向排水,其余外江水闸定向引水,此为连通方案3。研究此连通方案下,河网水流是否能维持单向流动,将其水量引进与水质改善等情况与方案2对比,同时可验证图论方法对水系结构连通性诊断的适应性。
d)经上述图论最小阻力计算及分析结果,拟定数值模型细化方案设置见表3 。
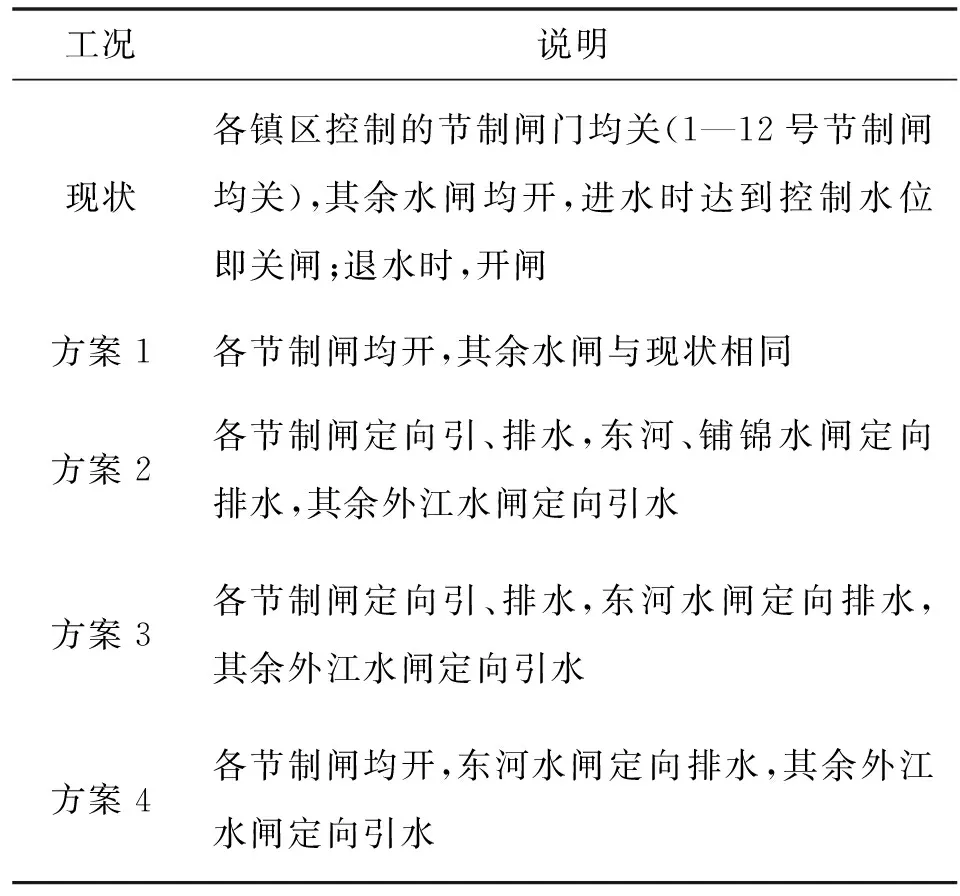
表3 工况设置
4.2 数值模拟计算成果比对分析
4.2.1模型构建及验证
建模区域为中顺大围主要河涌凫洲河、西部排水渠、岐江河相连接的大小河涌,根据中顺大围现状河道情况,对其概化,整个河网模型共1 511个断面,140个河段,251个汊点,28个边界水闸,12个节制闸。
模型对象主要为水动力参数,率定时间为2014年5月2日15:00至5月4日3:00,以岐江河中段同步水位观测资料进行模型参数率定,模型各水闸水位边界条件采用同时间段实测的潮位过程,闸门调度规则按照同时间段外江闸门实际开关设置,率定结果见图5a。模型的验证以2014年5月5日19:00至5月7日7:00的岐江河中段同步水位观测资料作为模型的验证资料,验证结果见图5b,可以看到计算值和实测值拟合较好计算与实测相差值均在10%以内,符合精度要求。本模型最终确定的水动力参数gama取0.85,Manning总体取值为0.02,部分取值为0.010~0.035。
4.2.2成果分析
一维水动力水质模型对以上拟定4个方案模拟计算得到表4。由现状与方案1的比较验证了,在感潮河网区,仅仅打开节制闸,恢复其天然连通对于河网的总引进水量基本无贡献,这就是所谓的“连而不通”的问题,究其原因,就是因为感潮河网河流受来水及潮流的双重影响,流速时正时负,区域水体呈现反复回荡情况,污染物无法排出河网,逐渐累积,使水生态环境恶化。方案2与方案1的对比可知:将河网内水体通过闸泵调度控制为单向流动,能使围内总引进水量大幅增加,增加幅度为227.5%;使水体更新速率从原来的9.37 d缩短为3.08 d,缩短了63.92%。河网采样断面污染物浓度合计也大幅下降,从501.18 kg/m3下降至87.59 kg/m3,证明使河网内的水流变为单向流,改善河网的水动力的基本思路是正确的。实际上,河网水系中的水流在人工控制下都变成单向流后,河网整体流速增加,流动性增强,水力连通性得以增加,这对于区域水体的循环更新速率及自净能力有很大的增益。
方案3与方案2的对比可知:仅将东河水闸作为排水闸的效果比同时将铺锦水闸、东河水闸的效果要好。证明了基于水流阻力与图论“最短路”思想构建的最小阻力路径计算工具能有效应用于河网调水方案的优化;方案3、4的结果表明:将各节制闸全开,无需定向引、排水,提高了围内河网的连通保证率,更有利于水体交换,达到更好的调水效果。
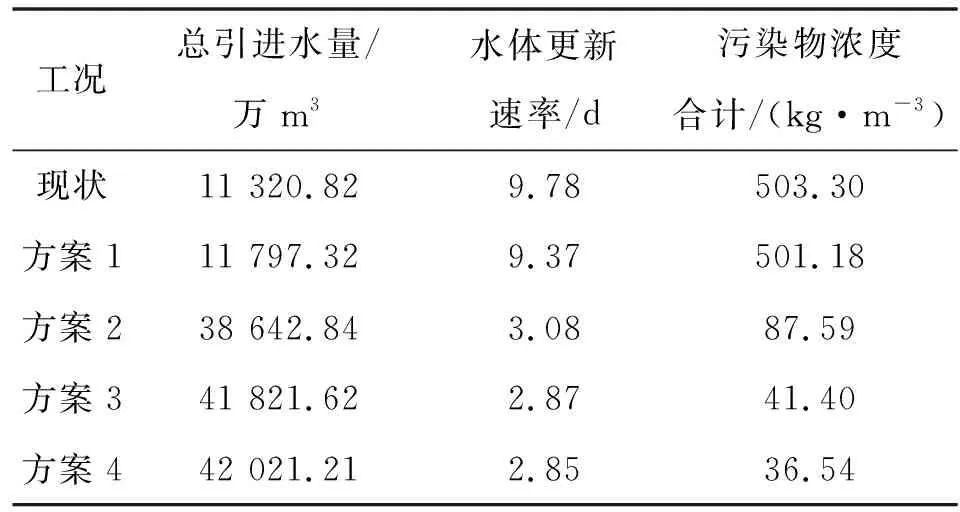
表4 现状与各方案下的连通效果对比
由前文所述优化思路进行的连通方案结果对比与验证,可以看到:基于水流阻力与图论的“最小阻力”分析方法可拟定初步的连通方向,并通过一维数值模型逐步细化连通方案,解决连而不通的问题。
5 结论
a)采用图论的最短路思想构建中顺大围图模型,引入水流阻力建立加权邻接矩阵,分析得出连通线路规划为从西河水闸引水,东河水闸排水,其阻力最小为192.36,可初步拟定最优连通路线为西河引水,东河排水。在图论拟定的初步方案基础上,进一步细化连通方案,通过设置节制闸的调度方式,采用一维水质水动力模型对联通后的河道总引水量、水体更新速率、污染物浓度等参数进行分析,得出最优连通方案。
b)通过数学模型对图论规划的方案2及方案3 两个不同的连通路线水质、水体更新率等参数的变化情况,可以得知图论得出的阻力较小的方案3比阻力较大的方案2具有更好的连通效果,由此可知图论方法可有效规划连通方案。
c)基于“水流阻力”与图论“最短路”思想,采用图论方法判定水系结构连通性,初步拟定连通方案,再进一步由数值模型细化方案解决连而不通的问题,该方法丰富了河湖连通性诊断手段,同时减少了数学模型需设置多工况反复对比计算而产生的巨大工作量,提高了规划效率,可为感潮河网区域的水系连通规划提供极具意义的参考。
