基于多模型集合方法的北江流域月径流预报研究
2022-07-02钟逸轩廖小龙全栩剑李媛媛
钟逸轩,廖小龙,全栩剑,易 灵,陈 艳,李媛媛,薛 娇
(中水珠江规划勘测设计有限公司,广东 广州 510610)
月径流模拟计算对于流域中长期水文预报、水资源优化配置、流域防汛抗旱、水电站发电计划制定等工作具有重要作用。现有月径流模型主要可分为统计模型、水量平衡模型、人工智能模型等。统计模型以季节性自回归模型(Seasonal Auto-Regressive model,SAR)为代表,通过建立降水量、蒸散发量以及前期月径流与当月径流之间的统计关系开展模拟计算[1]。水量平衡模型[2]以水量平衡原理为理论基础,将水文循环的各变量间的关系概化为经验公式,以实现流域月径流模拟计算,这类模型以熊立华等[3]提出的两参数月水量平衡模型(Two-Parameter Monthly Water Balance model,TPMWB)为代表,取得了广泛应用验证。人工智能模型主要基于人工神经网络 (Artificial Neural Network,ANN)[4-5]来模拟水文气象变量与月径流之间的关系,从而模拟月径流过程,近年来随着深度学习技术的推广普及,人工智能模型也越来越多地应用在月径流模拟计算问题上,获得了良好的应用效果。同时,研究表明[6-7],由于水文预报过程中始终存在着各种不确定性来源,尚无任何单个模型能够始终具有最佳计算精度,通过对多个模型结果进行集成,能够对各预报方案扬长避短,有效提高预报精度。
北江发源于江西省信丰县石溪湾[8],是珠江水系的第二大支流,流域面积46 710 km2。北江干流自北向南贯穿广东省中北部地区,全长约468 km,平均坡降约为0.26‰。北江流域地处亚热带季风气候,高温多雨湿润,多年平均降水量约为1 736 mm,水资源较为丰富,但流域降水的年内分配较不均匀,导致径流年内变化较大,不利于水资源开发利用。流域内主要水利枢纽工程有飞来峡水利枢纽、孟洲坝水电站、蒙里水电站、白石窑水电站、西牛水利枢纽、南水水库、锦江水库等,且社会经济较为活跃,因此准确可靠的月径流模拟计算结果对于北江流域的社会经济发展与保障社会安定具有积极意义。然而,现有文献针对北江流域开展的月径流模型研究较少,缺乏对不同月径流模型在北江流域的应用效果的分析验证,不利于充分发挥北江流域水利工程体系的兴利除害功能,亟需开展相关研究为北江水资源开发利用工作提供有效决策支持,为实现数字孪生流域建设提供帮助。
为获取准确可靠的北江流域月径流预报结果,本文选取北江流域坪石站、犁市站、横石站和石角站的月径流过程为研究对象(图1),综合分析对比了不同的月径流模型的应用效果,并基于BMA方法给出了多模型集成方案。采用数据包括北江流域降水量、潜在蒸发量以及相关站点月径流数据,时间范围为1970—2010年,研究成果可为北江流域的月径流模拟计算及中长期水文预报工作提供参考。
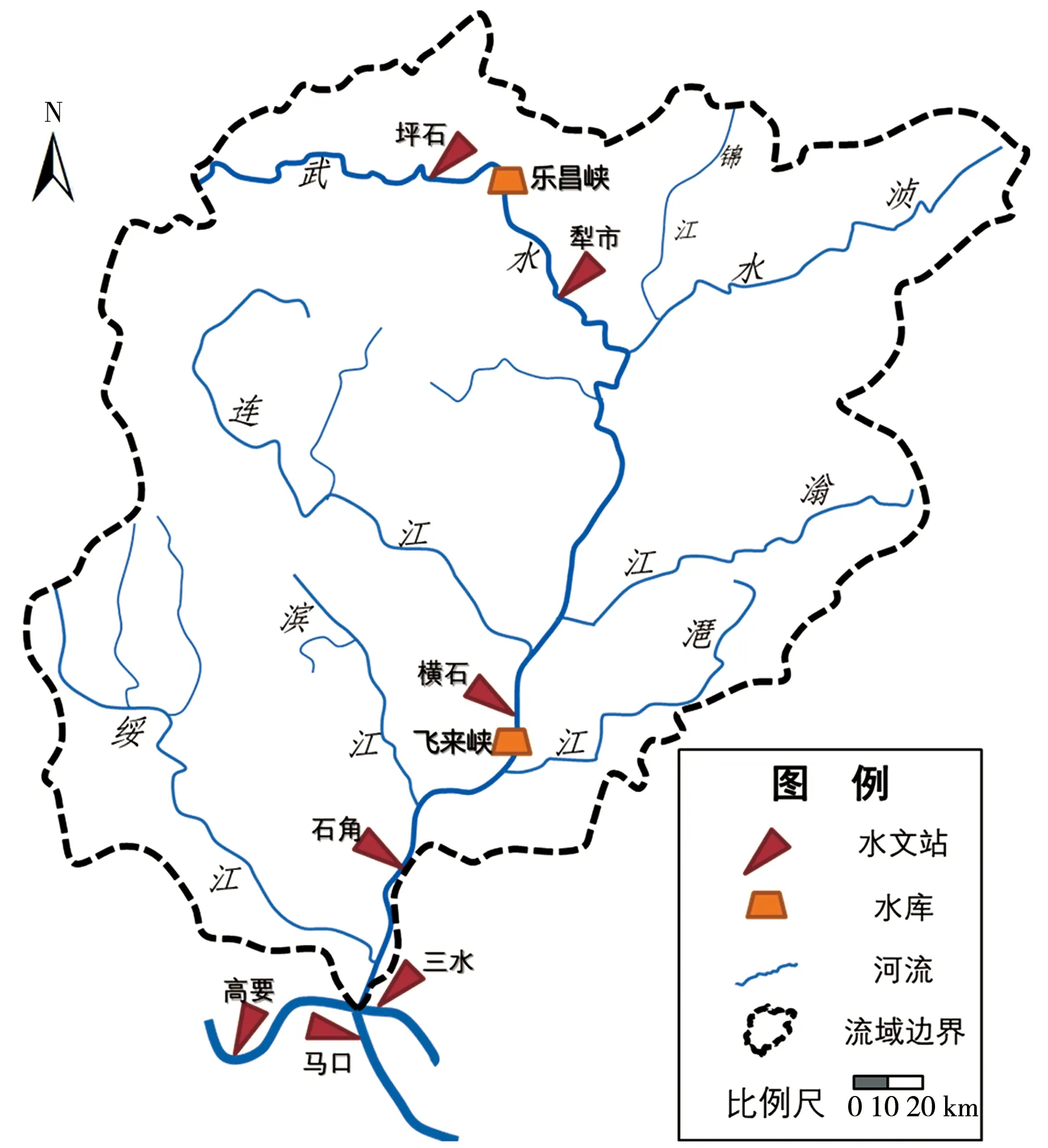
图1 研究区域示意
1 方法介绍
1.1 季节性自回归模型(SAR,Seasonal Auto-Regressive)
季节性自回归模型在水文预报和随机径流模拟中有广泛的应用,具有模型结构简单,计算效果良好,广泛适用于年均降水量、月径流量、日均流量等具有周期变化特点的非平稳随机变量的模拟计算问题。武兰婷等[1]利用金沙江仁里水文站的实测月径流序列,通过建立混合SAR模型,取得了良好的模拟预报精度。孟明星等[9]基于SAR模型开展了葛洲坝水库入库月径流预报,并对模型应用问题展开了讨论。ZHONG等[10]基于一阶SAR模型获取了三峡水库入库流量随机序列,结果表明随机序列具有与样本数据基本一致的统计特性。用于月径流模拟预报的SAR模型用公式表示如下:
Qt,η=φ0,η+φ1,ηQt,η-1+…+φp,ηQt,η-p+εt,η
(1)
式中φi,η——第η月的第i个自回归参数;Qt,η——第t年中第η月的模拟月流量;εt,η——误差项。
已有研究结果显示,采用一阶季节性自回归模型通常可取得良好的月径流模拟预报效果。
1.2 两参数月水量平衡模型(TPMWB)
两参数月水量平衡模型由熊立华等[3]提出,该模型的输入为降水量和蒸发皿观测值,输出为实际蒸发量、径流深等[11]。TPMWB模型具有参数少且容易优化、模拟精度高等优点[12],现已广泛应用于不同流域,如乐通潮等[11]运用两参数月水量平衡模型对汉江流域上游地区进行了模拟验证,计算结果具有较高的纳什效率系数;陈吉琴等[13]利用模型在西汉水流域上进行模拟,模拟结果相比实测值具有较小预报误差。两参数月水量平衡模型的计算流程如下。
a)推算实际蒸发量E。已知月降雨量P(t)、月蒸发皿观测值Ep的条件下,则流域实际的蒸发量由式(2)计算:
E(t)=C·Ep(t)·tanh(P(t)/Ep(t))
(2)
式中E(t)——第t个月的实际蒸发量;Ep(t)——第t个月蒸发皿观测值;P(t)——第t个月的降雨量;C——第一个模型参数。
b)扣除蒸散发以后的土壤含水量为:
W(t)=S(t-1)+P(t)-E(t)
(3)
式中S(t)——第t个月的土壤净含水量。
模型计算开始时需要任意给定S初值,并给定合适的模型预热期。
c)计算月径流量Q(t):
Q(t)=S(t)·tanh(S(t)/SC)
(4)
式中 SC——第二个模型参数。
d)更新土壤净含水量S(t):
S(t)=S(t-1)+P(t)-E(t)-Q(t)
(5)
本研究为提升参数优化效率,基于GPU技术运行遗传算法开展了参数优化,获取了北江流域各水文站对应的最优模型参数C和SC。
1.3 人工神经网络(ANN)
人工神经网络,是一种模仿生物神经网络的结构和功能的数学模型或计算模型,可有效应对各类具有高度非线性、模糊性和不确定性的问题,近年来被广泛应用于中长期水文预报领域。李克飞等[14]针对三峡水库采用ANN等模型开展了逐月入库径流预报,为三峡水库中长期调度提供决策支持。赵鹏雁等[15]分析对比了不同月径流模型在澜沧江流域中长期预报的应用效果,结果表明人工神经网络模型具有较好的预报表现。
ANN模型通常由输入层、隐含层和输出层3部分组成,对于水文预报问题,通常可采用m-1-1形式的ANN模型,即模型包含m个输入变量,1个隐含层和1个输出变量。模型结构见图2。本研究中,选取北江流域各水文站的上月径流量、多年平均月蒸发能力、月降水量作为预报输入量,则ANN模型可表示为:
Q(t) =f(Q(t-1),P(t),ET(t))
(6)
式中P(t)——第t月降水量;ET(t)——第t月对应的多年平均月蒸发能力;f(·)——ANN函数,其中隐含层响应函数采用Sigmoid函数的形式。
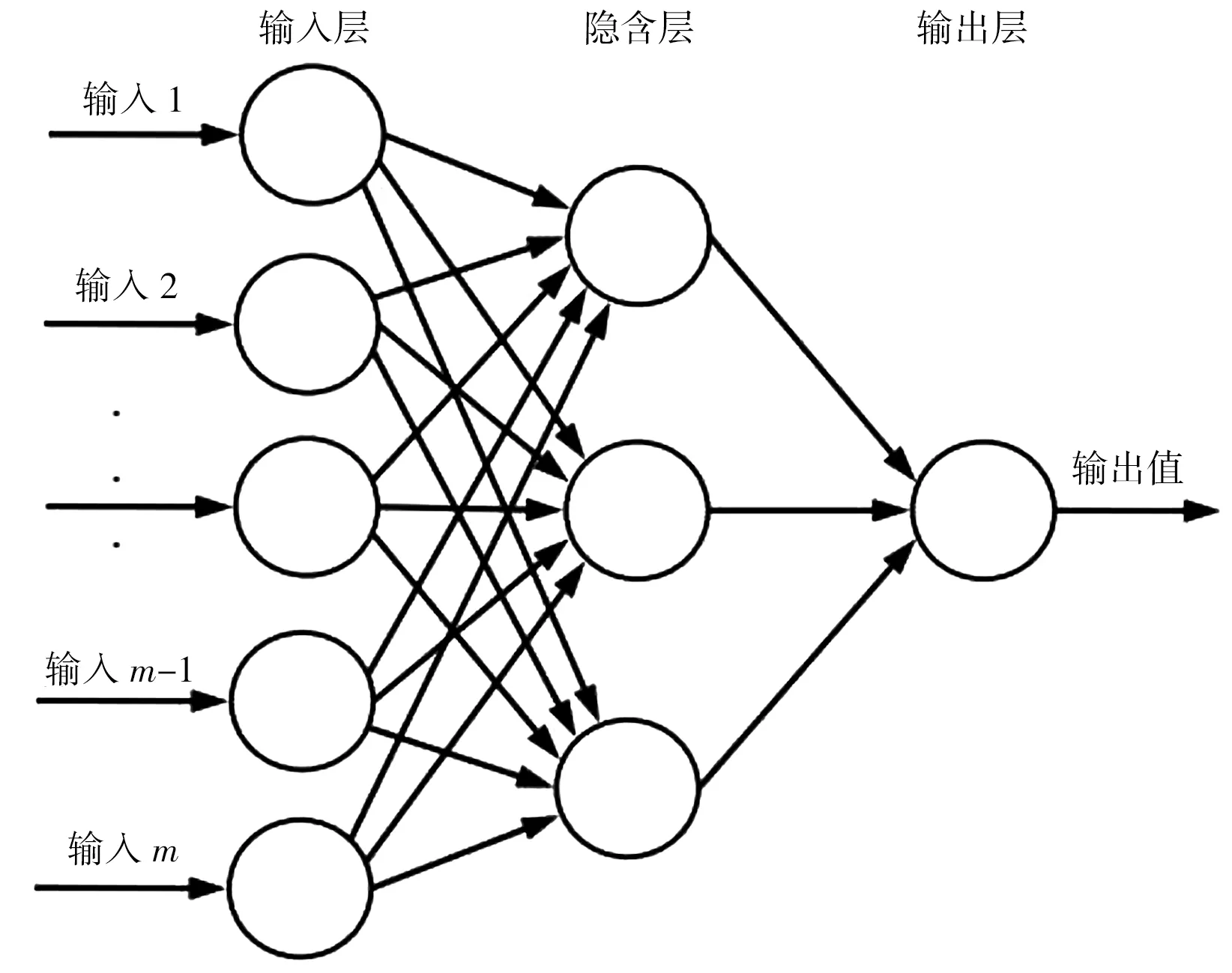
图2 月径流预报ANN模型结构示意
1.4 多模型集成预报
水文预报过程中广泛存在着各种不确定性,由此导致预报结果与实际值之间不可避免地存在误差,为此学者们提出采用多模型集成的方法予以解决,现有研究常采用的多模型集成方法有贝叶斯模型平均法[16-17](BMA)、集合模型输出统计法[18-19](Ensemble Model Output Statistics,EMOS)、深度学习算法[20-21](Deep Learning,DL)等。董磊华等[22]基于BMA方法开展了水文模型不确定性分析,结果表明BMA法能够有效降低模型不确定性,获取更为准确的预报结果。李宏亮[23]分别采用加权平均法、神经网络和多元线性回归模型对漓江桂林断面的3组中长期预报结果进行了集成,相比原预报结果精度显著提升。赵泽谦等[24]通过NSGA-II算法对6种模型计算的汉江黄金峡水库中长期预报结果开展集成,有效提升了预报准确性。
考虑到BMA法不仅可获取多模型集成预报,同时可为后期开展不确定性概率预报提供支撑,本研究最终选择BMA法获取了上述3种月径流预报结果的优化权重值。BMA法的本质是对实测值与各集合预报成员的条件概率分布进行加权平均,以此推求实测值的后验分布。本文仅对其简要介绍,具体可参考文献[25-26]。令Q(t)代表t时刻的实测值,Fi(t)代表第i个模型第t时刻的预报值,则基于集合预报Fi(t)(i=1,2,…,m)的实测值BMA后验分布可表示为:
(7)
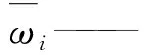
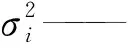
特别地,当Q和Fi的边缘分布均为正态分布时,上述条件概率分布也为正态分布,此时式(8)可改为:
(8)
式(8)即为基于正态分布的BMA概率预报的分布函数形式,其参数可通过期望最大值算法(Expection-Maximization)获取[26]。
对于边缘分布不服从正态分布的Q和F序列,常采用Box-Cox变换将其转换至正态空间再进行计算[27]:
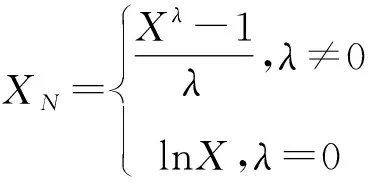
(9)
式中X——原始不服从正态分布的序列;λ——Box-Cox变换系数,可通过极大似然法确定;XN——变换后的数据序列。
在获取BMA优化权重值的基础上,对各模型预报结果加权平均得到多模型集成预报:
Qens(t)=∑ωi·Qi(t)
(10)
式中Qens——多模型集成预报;Qi——第i个模型的预报结果;ωi——第i个模型的优化权重值。
1.5 评价指标
采用水文情报预报规范[28]中推荐的确定性系数(DC)和水文预报广泛采用的平均相对误差绝对值[29](MAPE)作为评价各预报模型精度的指标。DC取值越接近1,MAPE取值越接近0,表示模型预报精度越好。
DC计算方法如下:
(11)

MAPE的计算方法如下:
(12)
式中各项同前。
2 结果分析
2.1 不同模型预报精度评价
对北江流域坪石站、犁市站、横石站和石角站采用不同方法开展了月径流预报,选取1970—1997共计28年作为模型率定期,1998—2010共计13年作为模型检验期。表1列出了3种模型的输入数据结构,其中,TPMWB模型考虑了流域水文循环原理,其输入量仅需当月降水量P和蒸发量E;SAR和ANN属于数据驱动模型,为增加模型获取的信息量,以提高计算精度,输入额外引入了前一个月的径流量Q。

表1 模型输入数据及参数优化方法
表2给出了3种月径流预报模型在北江不同水文站率定期和检验期的预报精度评价结果。结果表明,本次采用的3种月径流预报模型在北江流域各站点均具有较好的表现,率定期DC值位于0.86~0.91之间,检验期DC值除横石站TPMWB模型外,均位于0.81~0.90之间,且各站不同模型预报结果均具有较小的相对水量误差。率定期内,SAR模型和ANN模型具有相较TPMWB模型更优的DC值,其可能原因是前面2种数据驱动型模型额外使用了上一个月径流量作为输入,增加了预报信息量,同时相比TPMWB模型具有更多模型参数,因此率定期取得了更好的预报效果。检验期结果则相反,TPMWB模型在大多数站点具有更优的DC值,表明具有物理机制的水量平衡模型具有更强的泛化能力,模型稳定性更好。同时由表2结果可看出,北江流域各水文站在不同评价指标或不同模型计算时期条件下,对应的最优模型也不完全相同,充分说明北江月径流预报存在明显的模型不确定性,有必要采用多模型集成方法削弱模型不确定性对预报结果的影响,提高预报精度。
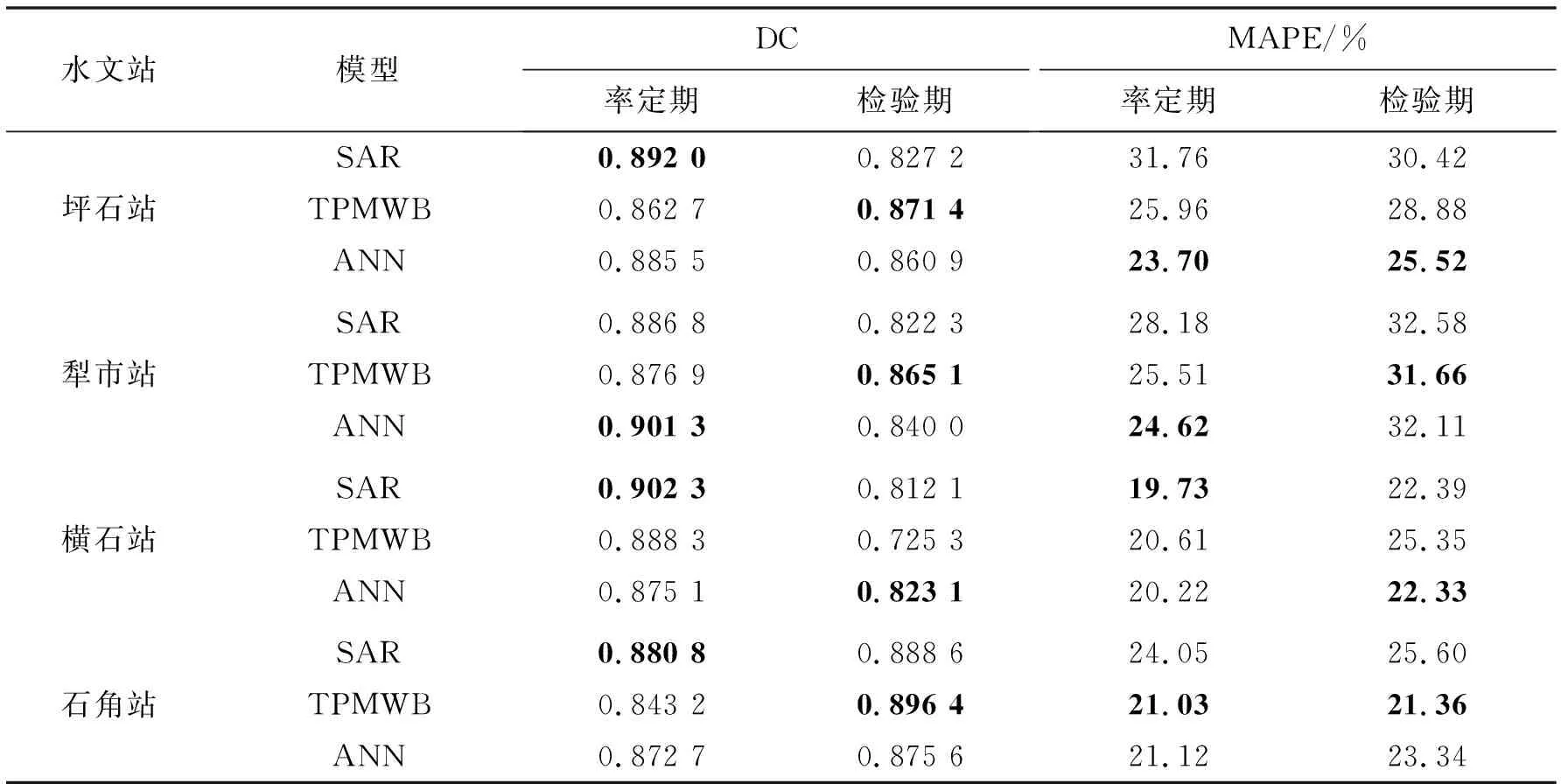
表2 3种月径流预报模型精度评价结果
2.2 多模型集成预报效果
采用BMA法通过计算实测流量的先验概率,并基于前述3种模型的月径流预报结果获取了预报值的后验分布,进而通过似然函数得到3种模型的优化权重值。表3给出了北江流域各水文站多模型集成预报各模型的权重值。表4给出了多模型集成预报精度评价指标与单模型预报指标最佳结果对比。
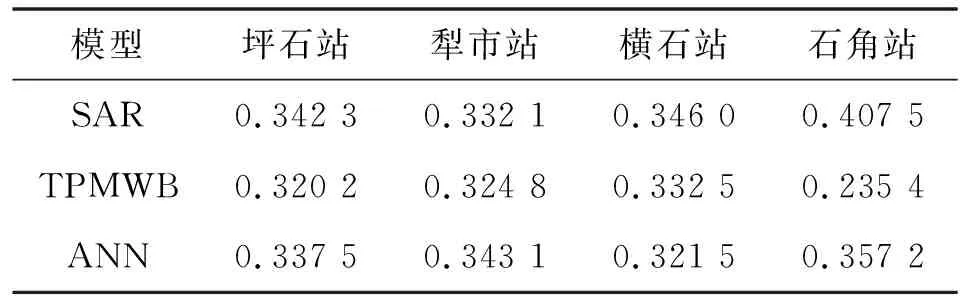
表3 北江各水文站月径流预报模型优化权重值
由表3可知,SAR模型对于坪石站、横石站和石角站有最大权重,ANN模型对于犁市站有最大权重。由于权重越大表明该模型在率定期具有越好的预报效果,表3中的结果与表2结果基本一致,即DC值较大且MAPE较小的模型能够获得较大权重值。同时,通过对比表4中多模型集成预报效果与单模型最优指标可知,基于BMA法获取优化权重对原始预报结果进行加权平均后,北江各水文站的月径流预报确定性系数和水量误差均有所提升,以犁市站为例,多模型集成预报的DC值不仅优于任意单一模型结果,还有效降低了预报水量误差,率定期和检验期的MAPE值分别下降2.65%和4.16%。对于中长期预报而言,水量误差大幅降低能够显著提升预报应用效果,因此基于BMA法加权平均的多模型集成预报能更好地为北江流域兴利除害提供决策支持。
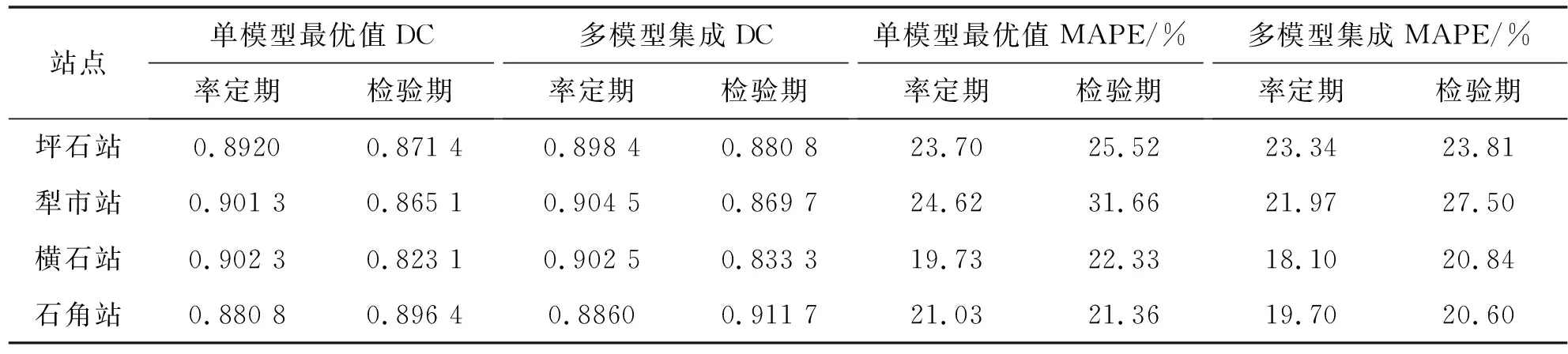
表4 北江各水文站多模型集成预报与单模型最优结果对比
为直观展示不同模型在率定期和检验期的预报精度,图3、4分别给出了率定期和检验期各北江流域各水文站实测月径流与预报结果的散点图,同时计算了二者的相关系数,限于篇幅,图中仅展示了横石站计算结果。由图3、4可知,横石站月径流预报结果散点图基本接近1∶1线,预报值与实测值之间相关系数ρ均位于0.9以上,具有较好的预报效果。同时,多模型集成预报在率定期和检验期均具有最高的相关系数,表明该方法可获取与实测值最接近的预报结果。综上所述,推荐将多模型集成方法用于北江流域各站点的月径流预报。
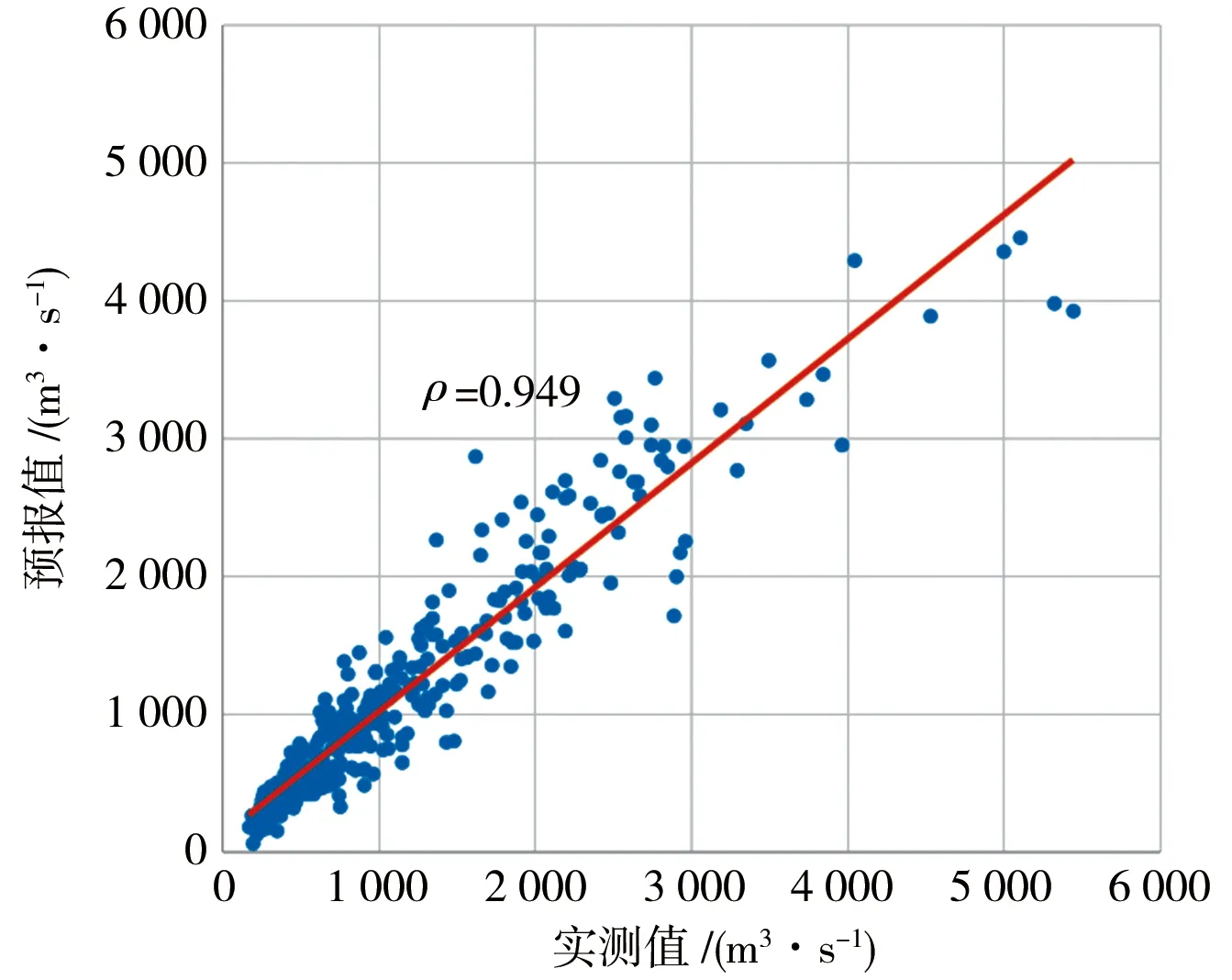
a)SAR
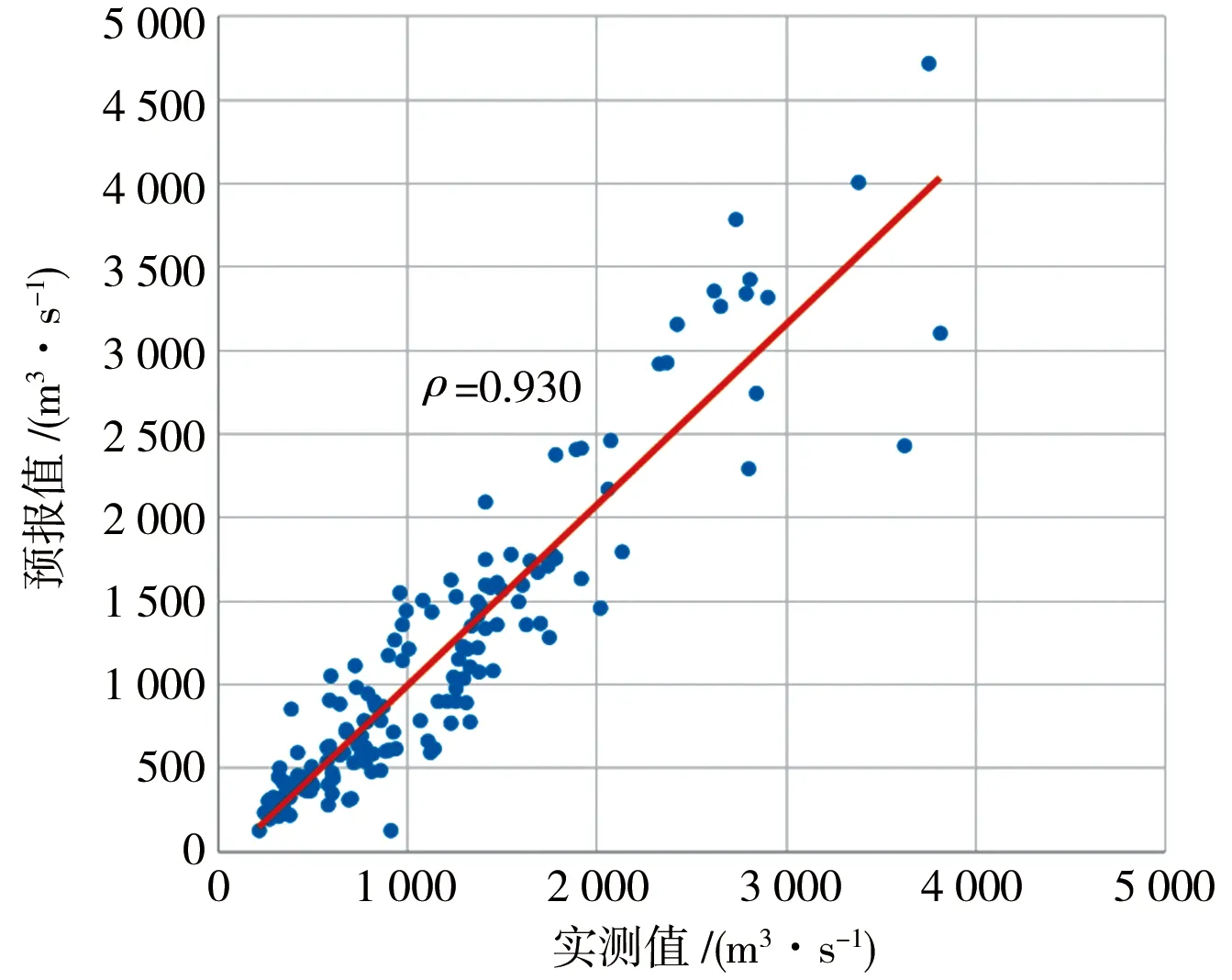
a)SAR
3 结论与展望
本文以北江流域坪石站、犁市站、石角站、横石站为研究对象开展了月径流预报研究,分析对比了3种常用月径流预报模型在研究区域的应用效果,并构建了基于BMA法的多模型集成方案,下面是主要研究结论和展望。
a)3种月径流模型在研究区域均具有较好的预报精度,率定期DC值位于0.86~0.91,检验期基本位于0.81~0.90,同时具有较小MAPE值,表明月径流预报具有较好的拟合精度和较小的水量误差。其中SAR模型和ANN模型具有更优DC值,表明增加输入信息一定程度上能够提升预报精度,而具有物理机制的水量平衡模型TPMWB则具有较小的水量误差和更好的泛化能力。
b)采用各站3组月径流预报率定期成果进行BMA权重优化,结果显示坪石站、横石站和石角站均为SAR模型权重值最大,而犁市站ANN模型具有最大权重,充分说明BMA法对于拟合精度较高的预报方案通常能够给出更高的优化权重值,并兼顾了不同模型的优势互补。
c)北江流域各站多模型集成后的月径流预报具有相较任一单模型方案更优的DC值,还能有效降低预报水量误差,显著降低了MAPE值,能够为北江流域兴利除害提供更为准确的中长期预报信息;同时在实际应用中,应逐步积累经验,分析多模型集成预报精度提升的效益相比其时间和经济成本是否具有明显优势,探索如何令多模型集成更好服务实际。
d)后续研究工作中,可在本文考虑模型不确定性的基础上,进一步探讨输入不确定性和参数不确定性对北江流域月径流预报的影响,将多模型集成方案扩充为月径流不确定性概率预报方案,并研究中长期水文预报信息对城市防洪排涝的作用[30],以期为流域管理部门制定调度决策方案提供更加准确和全面的中长期预报支撑。
