叠梁的变形与弯曲切应力影响的关系讨论

2022-07-02胡伟平孟庆春詹志新

力学与实践 2022年3期

李澳胡伟平孟庆春詹志新

(北京航空航天大学航空科学与工程学院，北京 100191)

在材料力学中，梁的应力分析是非常重要的一部分内容。其中包括弯曲正应力分析和弯曲切应力分析。学生对于弯曲正应力的分析过程比较容易接受，因为其体现了材料力学中杆件应力分析的最基本方法，即从实验观察到变形规律假设，再到几何方程、物理方程和平衡方程，最后得到应力解答。而弯曲切应力的分析相对比较抽象，其核心是基于分离体的平衡和切应力互等定理，并假设了纯弯正应力公式仍然适用于横力弯曲的情况[1-3]。很多文献对这一解法的近似性进行了讨论[4-6]，对于一般细长实心梁，这一解答足够精确。但是，弯曲切应力的分析模型不是从变形观察开始的，这主要是由于梁弯曲时剪切变形并不明显，难以直接观察。如果能够通过简单的演示实验来说明弯曲切应力的存在，使学生先有直观感性认识，则有助于提高学生对于后续理论推导的兴趣，并启发学生将理论与实际紧密联系。

关于梁弯曲切应力存在的演示实验主要有两种，第一种是用木梁的弯曲破坏实验[7]，通过木梁沿纵向截面破坏能够很好地演示弯曲切应力的作用效果，但是一般不便于现场演示；第二种是对比叠梁和整体梁的弯曲变形[8]，通过两种变形的不同来说明层间存在切应力。在现场演示时可采用橡胶或硅胶材料制备叠梁和整体梁，以便于明显观察到两种不同的变形效果。对于第二种演示实验，初想之下，觉得能够很好地说明层间切应力的存在。但仔细分析后，发现有可能引起概念上的混淆。下面就来具体讨论一下。

1 叠梁与整体梁弯曲变形的对比

采用相同材料制备叠梁和整体梁。叠梁由两个尺寸相同的梁无摩擦叠合而成，如图1(a)所示。整体梁的尺寸与两个叠合起来的梁的总体尺寸相同，如图1(b)所示。叠梁和整体梁均在左侧固支，右端施加集中力。

图1 叠梁和整体梁结构及载荷示意图

随着载荷的增加，叠梁发生弯曲变形，由于上下梁之间是无摩擦叠合，上下梁各自独立弯曲，可以认为上下梁的弯曲曲率相同[9]，则其变形图如图2所示。如果是橡胶或硅胶材料梁，可以观察到上梁的下表面与下梁的上表面之间存在明显的错动。而整体梁则是整体弯曲，各层之间无相对错动。整体梁可以视为由叠梁的上下梁之间完全粘接而成。因此，在整体梁中必然是由层间的相互作用力阻止了两层间的错动，这自然就是层间切应力了。由此可以得出结论，整体梁的层间存在切应力。上述分析符合直观感受，看似逻辑清晰，结论合理。但仔细思考之后，有几个概念需要辨析。

2 叠梁弯曲变形描述的辨析

首先，在叠梁的变形中，图2(a)变形现象是客观事实，确实能够明显观察到，即相比于图2(b)所示整体梁，叠梁上梁下表面与下梁上表面之间错开了。但是，这种现象与剪切引起两个面的相对错动完全不同。叠梁接触表面的错开恰好与剪切变形几乎无关，其主要是上梁下表面的缩短和下梁上表面的伸长所导致的，即这种错开的变形主要是两接触表面长度变化差别的反映。下面根据材料力学方法建立一个简单的分析模型来进行说明。图2(c)所示为考虑了叠梁由于弯曲切应力导致横截面翘曲后的弯曲变形示意图。

图2 叠梁与整体梁的变形示意图

不考虑横截面翘曲时，上下梁接触处的纵向长度变化差为

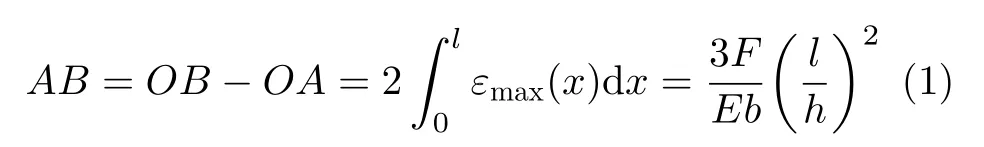
式中，l为梁的总长度，b为梁的宽度，h为单个叠梁的高度，E为材料的弹性模量，εmax为下梁的最大轴向正应变，即下梁上表面的轴向正应变。

当考虑两梁的剪切变形时，横截面产生翘曲。同时，由于沿梁长度方向剪力不变，即所有横截面的翘曲变形相同。因此上梁下表面产生附加长度变化AA′，下梁上表面产生附加长度变化BB′。

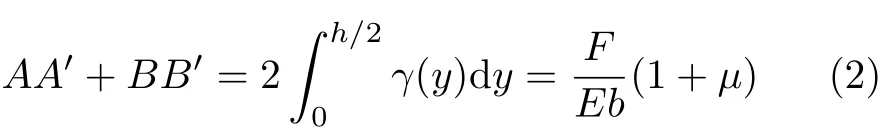
式中，γ(y) 为梁在y处的切应变，y坐标原点位于下梁轴线上，且垂直x轴朝向上为正，如图1(a)所示。G为材料的切变模量，µ为材料的泊松比。

对比式（1）和式（2），并考虑到一般梁满足条件l≥5h，可以看到，一方面梁的剪切变形实际上减小了接触面上下层的纵向长度变化差；另一方面，这种减小作用十分有限，相比于正应力导致的纵向长度变化差小一个数量级以上，可以忽略不计。

因此，虽然从直观来看，叠梁弯曲变形时上下梁的接触面错开了，但这种变形从力学性质上看主要是由上下层的纵向长度变化差所致，而与剪切变形相关的“错动”无关。

3 上下叠梁粘接作用的力学分析

前一节讨论了叠梁弯曲变形时导致上下梁接触面错开的主要原因，那么，将两梁粘接成整体梁后，粘接的层间在限制层间错开时到底是起到了何种作用？

一种基于直观的认识认为，既然是限制了两个面的错开，那么粘接必然是提供了面内的剪切应力。这种观点具有一定的迷惑性，因为从自身逻辑来看是正确的。但是在第2节中已经分析了，两个面的错开主要是由两个面的纵向长度变化不同引起的，并不是与剪切变形相关的“错动”。因此，不能通过施加剪切应力来抵消这种“错开”变形，必须通过施加正应力才能消除这种变形。这一概念正是符合广义力与其相应广义位移的基本概念。

3.1 纯弯叠梁粘接时的力学分析

通过上面的分析，叠梁的粘接面所起的主要作用应该是提供正应力而非切应力，这一点似乎违背了直观认识。为了更好地说明这一力学性质，先以纯弯梁为例进行分析。图3(a)所示为两端受线性分布正应力的一段纯弯叠梁。两层的粘接直接来说是提供位移约束，为了清楚理解这种位移约束的作用，将位移约束等效成力的约束，就像静不定问题分析时所采用的方法一样。假设不将叠梁粘接，而是通过施加载荷，如图3(b)所示，然后将图3(a)和(b)叠加得到整体梁受载时的应力分布，如图3(c)所示，则所施加的载荷就是与粘接作用等效的力的作用。

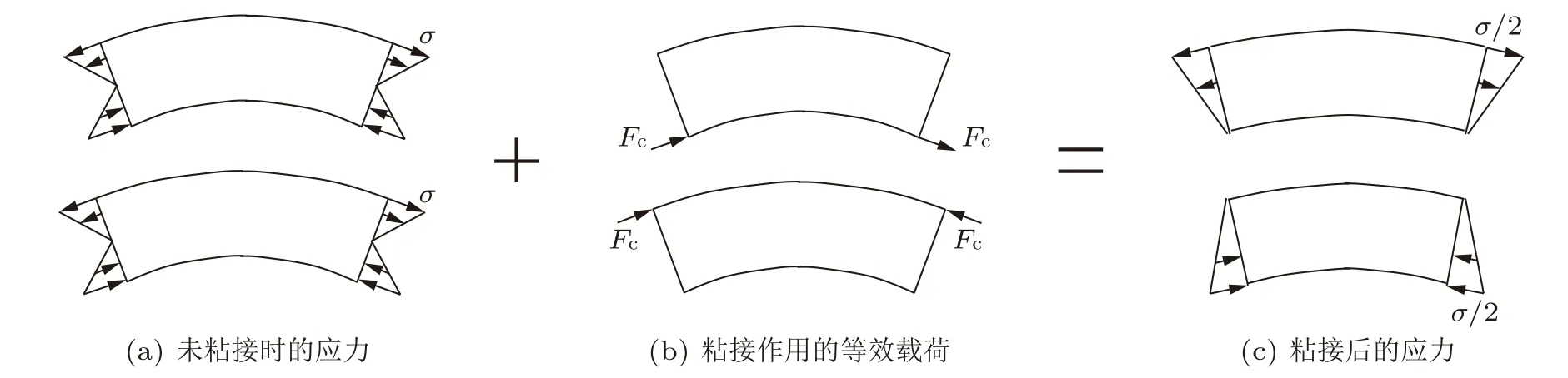
图3 纯弯叠梁粘接作用的力等效分析

假设单个叠梁高为h，宽为b，叠梁上下梁各自施加的最大应力为σ，则有

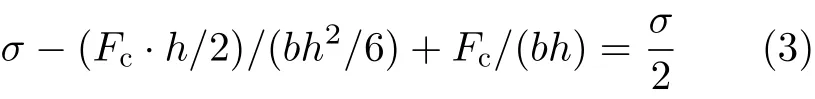
解得

因此，叠梁粘接时的位移约束可以等效为在接触面处施加了一个相互作用的沿轴向载荷，该沿轴向载荷使原来存在纵向长度差的两个面长度相等，并改变了整个横截面上的正应力分布。

这里有一点需要说明，接触面的载荷应该只能直接作用于接触面上，不能施加到梁横截面上。首先，直接接触处确实只能通过作用在接触面上的方式传载，但是在远离接触面后，根据圣维南原理，载荷作用效果等效成了沿轴向载荷。利用图4可以简单地说明这一点。图4(a)为一沿表面受载的杆，当分析远离载荷作用区域的AA′横截面上的载荷时，可以等效为图4(b)所示情况。进一步，可以得到AA′横截面上的应力分布，如图4(c)所示。其次，对于实际的粘接纯弯叠梁，其实只有两端的粘接面处会产生约束载荷，中间的粘接面并不产生约束载荷。图5所示的有限元计算结果说明了这一特点。图5(a)，(b)，(c)为两处粘接后的四点弯叠梁，以及受载后的正应力分布云图和切应力分布云图。图5(d)，(e)，(f)为四处粘接后的四点弯叠梁，以及受载后的正应力分布云图和切应力分布云图。两种情况下在靠近梁两端面的粘接处，正应力和切应力分布都比较复杂，远离粘接处之后，正应力呈现典型的纯弯梁正应力分布特点，而切应力则近似为零。同时，还会发现，有四处粘接的叠梁，在靠内的两个粘接面处正应力和切应力并没有呈现出不同，也就是说，靠内的粘接面上并没有提供约束载荷。这一计算结果与图4所示的分析模型相一致。

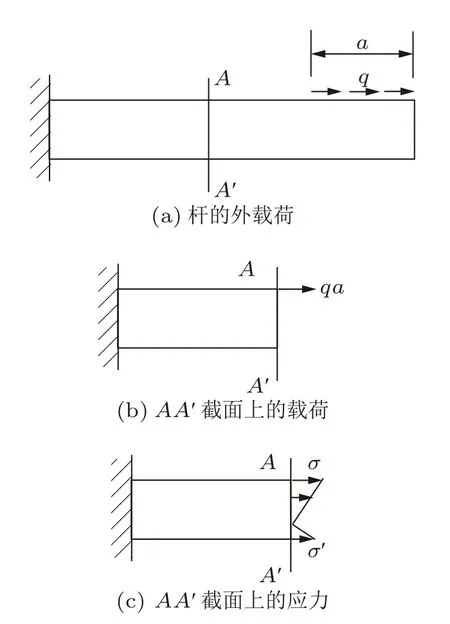
图4 作用于表面的载荷在远离力作用区域处的等效分析

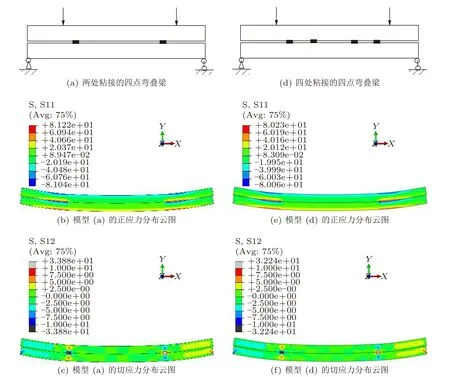
图5 纯弯叠梁不同粘接形式的效果对比

3.2 悬臂叠梁粘接时的力学分析

3.1节针对纯弯叠梁粘接时位移约束的等效力的作用进行了分析，然而在横力弯曲时，情况要复杂一些。下面，以图1(a)所示悬臂叠梁为例来分析粘接时的作用。从梁的x位置取一长为dx的微段，如图6(a)所示，该微段两侧截面同时作用有正应力和切应力。根据第2节的分析结论，接触面处的错开主要是由上下面的轴向长度变化不同造成的。进而，根据3.1节的分析，要使得上下面的长度相同，粘接的作用应等效为沿轴向载荷。直接利用3.1节的结果，得到接触面两端的沿轴向载荷。

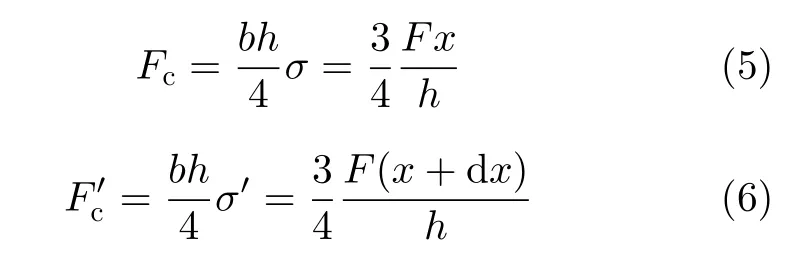
图6 悬臂叠梁微段粘接的力等效分析

但是，仅在接触面两端作用有Fc和F′c不能平衡，必须在接触面上还作用有Fs，即

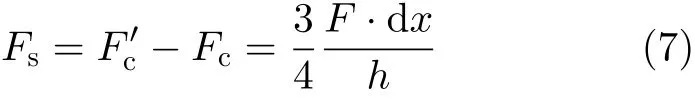
将图6(a)，(b)叠加，即得到图6(c)所示受力状态，接触面上的切应力为

这正是叠梁粘接成整体梁后的应力状态。因此，对于任意微段来说，粘接的作用等效为作用于接触面两端的沿轴向载荷和作用在接触面上的剪切载荷。并且，沿梁长度不同位置时，接触面端部的沿轴向载荷不相同，但接触面上的剪切载荷相同。将以上微段的受力分析推广到整个梁上，可以得到粘接作用的等效载荷形式，如图7所示。

图7 整个悬臂叠梁层间粘接作用的力等效

上述结果似乎说明了悬臂叠梁层间粘接作用正是在粘接面上提供了剪切载荷，而正是该剪切载荷才消除了叠梁接触面的错开。然而，这种说法会造成概念的混淆，这就好比在解释图4(a)所示杆件上表面伸长时，不能说是剪切载荷引起了杆件上表面伸长，而是应该理解为是横截面上的弯矩和轴力引起了杆件上表面伸长。因此，对于悬臂叠梁层间粘接作用的正确理解也应该是粘接作用在上下两梁横截面产生的附加正应力使得接触面上下层的纵向长度变得相同，从而消除了层间的错开。而此时层间剪切载荷对接触面上下层的纵向长度变化的直接贡献恰恰可以忽略，它的主要作用是平衡由于弯矩沿梁长度变化造成的两横截面上的纵向载荷差。反过来，就可以理解，通过叠梁层间错开的消失来证明整体梁层间必然存在切应力在力学概念上的不足之处了。