高匹配单边缺口拉伸试件J积分塑性因子研究1)

武 旭 谢 彬 谢文会 张明敏 韩旭亮 马晨波 邓小康

*(中海油研究总院有限责任公司，北京100028)

†(中国海上卫星测控部， 江苏无锡 214400)

管道断裂韧性通常通过小尺度试样实验测试确定，ASTM E-1820、BS EN ISO 15653、GB/T 21143等标准推荐采用单边切口弯曲（single edge notch bending, SENB）试样或紧凑拉伸（compact tension, CT）试样测试材料的断裂韧性，而两种试样的裂纹尖端约束较高，测试结果偏于保守。对于管道环向浅裂纹情况，裂纹尖端约束较小，采用SENT（single edge notch tension）试样的测试结果与实际情况更为接近[1-4]。同时，管道焊接接头以环向裂纹为主，因而更适合采用SENT试样测试管道焊接接头的断裂韧性[5-7]。

管道焊接区域容易产生裂纹、未焊透、咬边等平面缺陷以及孔洞、夹渣等体积缺陷，对管道的安全运营存在潜在威胁。为了解决此类缺陷对管道完整性的潜在影响，部分标准与规范要求焊缝金属强度高于母材强度，即采用高匹配焊接接头，这可以提高管道的总体强度。准确测试环焊缝断裂韧性对保障管道安全具有重要意义，而SENT试样J积分塑性因子的准确性是断裂韧性测试的前提。

关于J积分塑性因子，国内外学者主要进行了以下研究。文献[8-10]提出了J积分作为表征弹塑性材料裂纹尖端应力应变场的新参数。文献[11-12]利用能量释放率提出了J积分的实验评估方法，建立了表征含裂纹结构的J积分断裂准则，该方法需要采用多个试件进行测试。为简化测试流程，Rice等[13]又提出了J积分测试的单试件法，利用J积分塑性因子与载荷位移曲线下的面积进行计算。标准ASTM E1820规定了深裂纹SENB试样J积分塑性因子方程，亦有学者对裂纹长宽比（a/W）小于0.45的潜裂纹SENB试件J积分塑性因子方程进行了研究[14-16]。对于SENT试样，文献[17-18]分别针对母材和低匹配焊缝，采用有限元分析方法，提出对应的J积分塑性因子方程。然而，对于不含侧槽以及侧槽深度10%的高匹配SENT试样，尚未有文献介绍相关报导。

因此，本文针对高匹配焊接接头，采用三维有限元分析方法，建立试件厚宽比（B/W）等于1，不含侧槽与侧槽深度10%的SENT试样有限元模型，计算不同裂纹长宽比、匹配系数、焊缝宽度下的J积分塑性因子，分析裂纹长宽比、匹配系数、焊缝宽度、试件侧槽对J积分塑性因子的影响，拟合高匹配SENT试样的J积分塑性因子方程，为高匹配焊接接头的断裂韧性测试提供必要依据。

1 J积分塑性因子计算

J积分塑性因子与加载水平无关，是一个与a/W有关的函数。对于焊缝金属在确定载荷条件下，含侧槽与不含侧槽SENT试样的塑性J积分（Jpl）可以通过总的J积分与弹性J积分（Jel）进行计算，而Jel可由应力强度因子（K）确定[18]

式中，E和ν分别代表弹性模量和泊松比。其中，应力强度因子

式中，P为载荷，B和BN分别为试件的厚度与有效厚度，F(a/W)为与裂纹长宽比有关的多项式函数。

由数值计算所得J积分与弹性J积分可得到

载荷–位移曲线下塑性区面积（Apl）计算式为

式中，A为载荷–位移曲线下的总面积，Ael为载荷–位移曲线下弹性区面积，C0为加载柔度。

基于载荷线位移的J积分塑性因子（）和基于裂纹嘴张开位移的J积分塑性因子（）计算公式[18]分别为

式中，b为韧带长度，和分别为基于载荷线位移和基于裂纹嘴张开位移的载荷–位移曲线下塑性区面积，和分别为标准化塑性区面积和标准化塑性J积分。

2 有限元分析

2.1 高匹配SENT试样几何模型

采用三维有限元分析方法，建立高匹配SENT试样有限元模型，分析焊缝宽度、匹配系数、试件侧槽对J积分塑性因子的影响。试件宽度W为20 mm，厚度B为20 mm，即试件厚宽比B/W为1，夹持端距H离为200 mm，即H= 10W。裂纹长宽比a/W分别取0.2～0.7（增量为0.1），焊缝宽度比2h/W分别取0.5，0.75，1，即焊缝宽度h分别为5，7.5，10 mm，匹配系数My分别取1.1，1.2，1.3，1.4。模型分为侧槽深度10%B与不考虑侧槽两种，侧槽采用“V”形切口，切口角度为45°。

由于对称性，采用C3D8R单元建立1/4有限元模型，对称处施加约束，在试件端部施加位移载荷。图1为a/W= 0.5，2h/W= 0.5时含侧槽SENT试样有限元模型。其中侧槽沿坐标轴Z向网格划分为5层，有效厚度沿坐标轴Z向网格划分为10层。为了捕捉试件裂纹前沿较高的应力、应变梯度，试件网格沿坐标轴Z向从侧槽前沿至对称面和自由表面逐渐增大。为优化裂纹尖端网格，采用2.5 µm圆弧划分裂尖单元，该网格可以较为准确地计算裂纹尖端应力、应变场。

图1 含侧槽SENT试样有限元模型Fig. 1 Finite element model of SENT specimen with side groove

2.2 材料模型

材料模型采用Ramberg–Osgood本构关系进行描述，母材与焊缝材料的真应力应变关系可表征为[7]

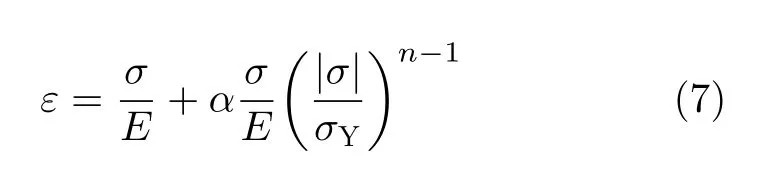
式中，σY为屈服强度，E为弹性模量，α为硬化系数，n为硬化指数。

为评估匹配系数对高匹配SENT试样J积分塑性因子的影响，σY= 410 MPa，n= 10，E=200 GPa，ν= 0.3。碳素钢的屈服强度通常随硬化指数的增加而增大，焊缝的硬化指数根据典型管道钢的屈服强度和硬化指数之间的关系进行估算，得到材料相关性能参数，见表1。

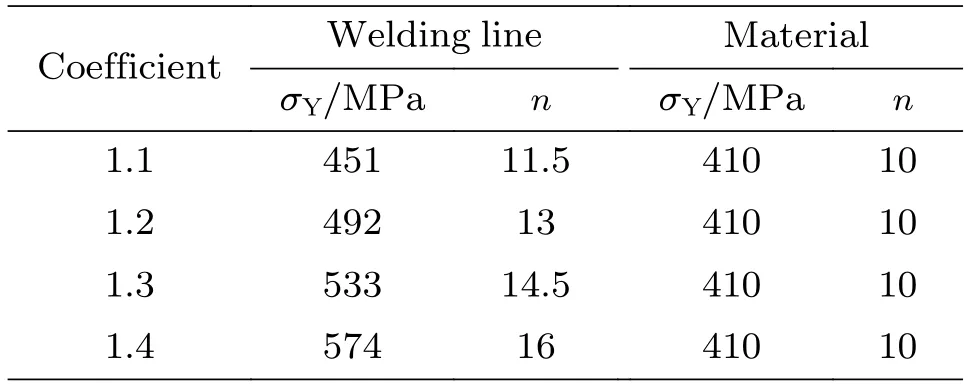
表1 SENT试件材料特性Table 1 Material properties of SENT specimen

2.3 分析过程

由于J积分与积分路径无关，同一平面内提取裂纹尖端19个环形路径J积分，J积分偏差不大于4.3%。厚度方向上，除自由表面外，将各层J积分取平均值用于塑性因子计算。模拟过程中采用位移载荷进行控制，在试件端面施加位移载荷，分2000个加载步，采用完全Newton–Raphson迭代法求解非线性方程组。每个高匹配SENT试样可以获得2000组载荷线位移、裂纹嘴张开位移以及J积分数据，按式（1）～式（6）计算J积分塑性因子。

3 结果分析

3.1 J积分塑性因子评估

图2为含侧槽高匹配SENT试样在a/W=0.6，My= 1.1，2h/W= 0.5时的塑性J积分和载荷位移曲线塑性区面积的对应关系。对于固定尺寸的高匹配SENT试样，曲线的斜率即为J积分塑性因子。可知对于高匹配SENT试样，在初始阶段随载荷增加逐渐下降，随着载荷的持续增加逐渐趋于常数。在整个加载范围内均保持恒定，表明与载荷大小无关。因此，选取J积分塑性因子处于线性部分的相关数据进行计算。不同几何结构、匹配系数下的高匹配SENT试样J积分塑性因子计算结果见表2。可知，试件B/W相同的情况下，含侧槽SENT试样的，明显高于不含侧槽试件。因此，建议在SENT试样断裂韧性测试中，根据试件侧槽情况选择对应J积分塑性因子方程，以提高测试精度。

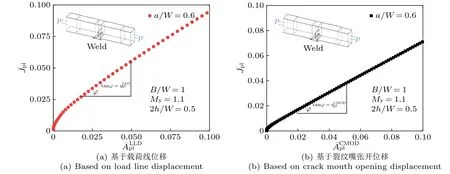
图2 含侧槽焊缝SENT的 − 示意图Fig. 2 Schematic diagram of − of SENT with side groove

3.2 焊缝宽度影响分析

为了评估焊缝宽度对高匹配SENT试样J积分塑性因子的影响，模拟了三种不同焊缝宽度SENT试样，即h= 5，7.5，10 mm。当B/W=1，My=1.1时，不同焊缝宽度下，不含侧槽SENT试样的和结果见图3。可知对于高匹配SENT试样，在所选定的3种焊缝宽度下，焊缝宽度对J积分塑性因子的影响相对较小，焊缝宽度的相关性可以忽略。对于侧槽深度10%B的含侧槽SENT试样，焊缝宽度对J积分塑性因子的影响与不含侧槽SENT试样类似，均可忽略。

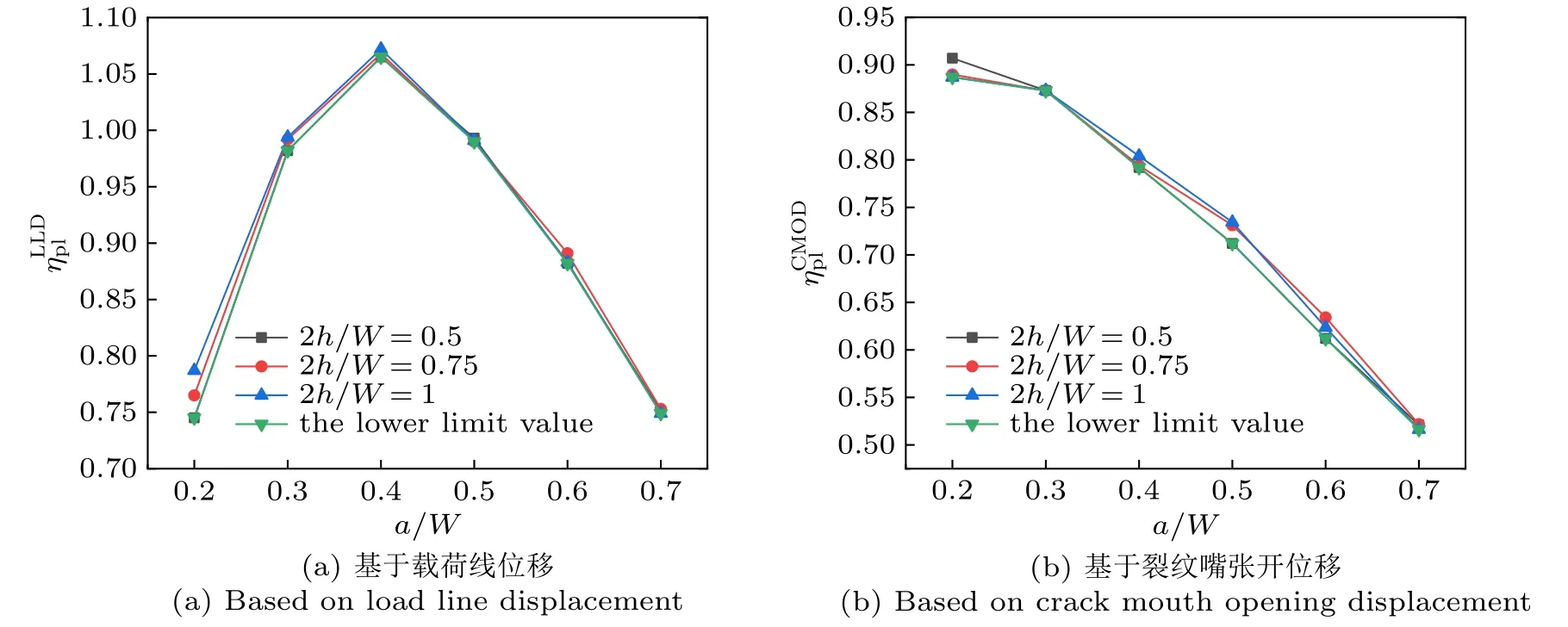
图3 不含侧槽试件焊缝宽度对J积分塑性因子的影响Fig. 3 Effect of weld width on J-integral plasticity factor of specimen without side groove

在研究匹配系数以及侧槽对J积分塑性因子的影响时，为了忽略焊缝宽度对J积分塑性因子的微小影响，相同试件厚宽比、匹配系数下，取不同焊缝宽度的J积分塑性因子下限值用于匹配系数以及侧槽的研究分析。由下限值来确定J积分阻力曲线，可以得到相对保守的结果，确保管道的安全性。

3.3 匹配系数影响分析

采用三种焊缝宽度（h= 5，7.5，10 mm）的下限值研究匹配系数对高匹配SENT试样J积分塑性因子的影响，图4表示不含侧槽SENT试样匹配系数对和的影响。对于不含侧槽SENT试样，和随匹配系数的增加而减小，而当a/W=0.3时，对匹配系数相对不敏感。而由表2可知，对于侧槽深度为10%B的SENT试样，当0.2≤a/W≤0.4时，对匹配系数不敏感，其余情况下和均随匹配系数的增加而减小。

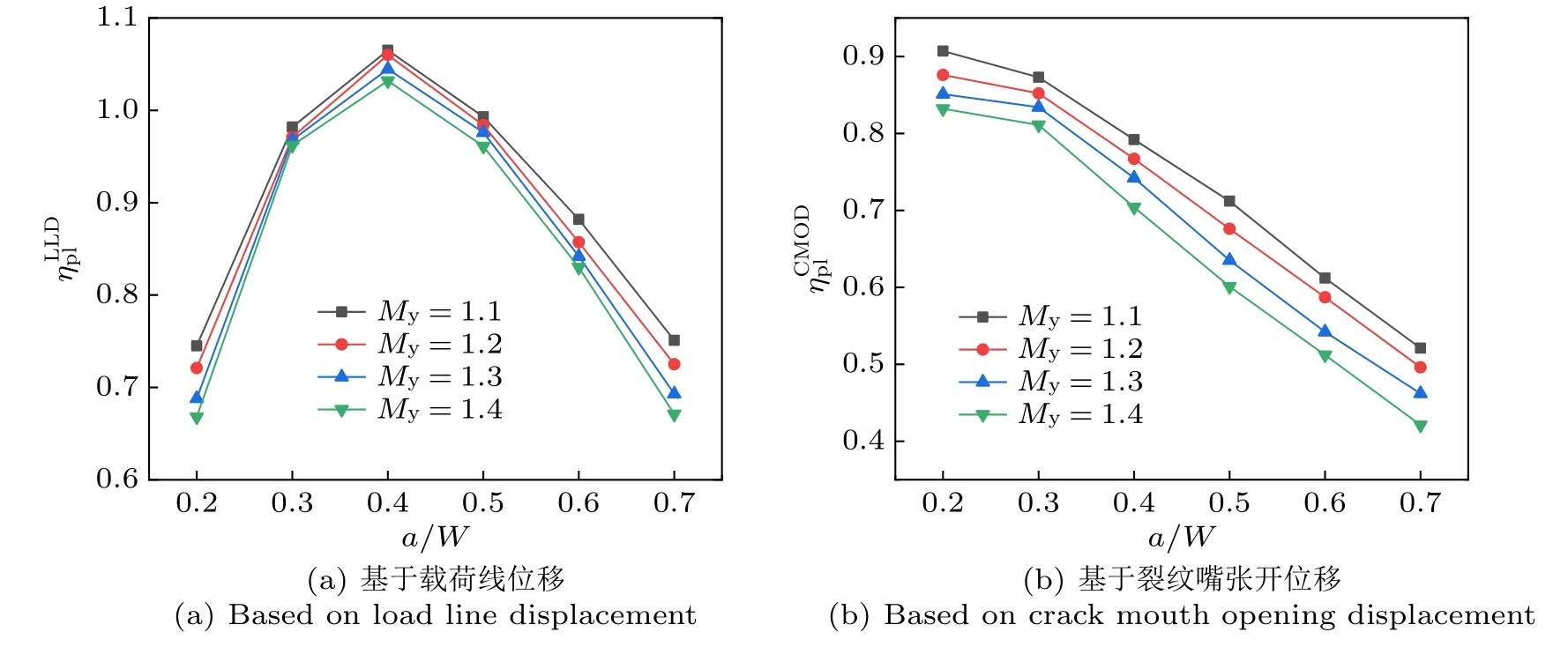
图4 不含侧槽试件匹配系数对J积分塑性因子的影响Fig. 4 Effect of matching coefficient on J-integral plasticity factor of specimen without side groove

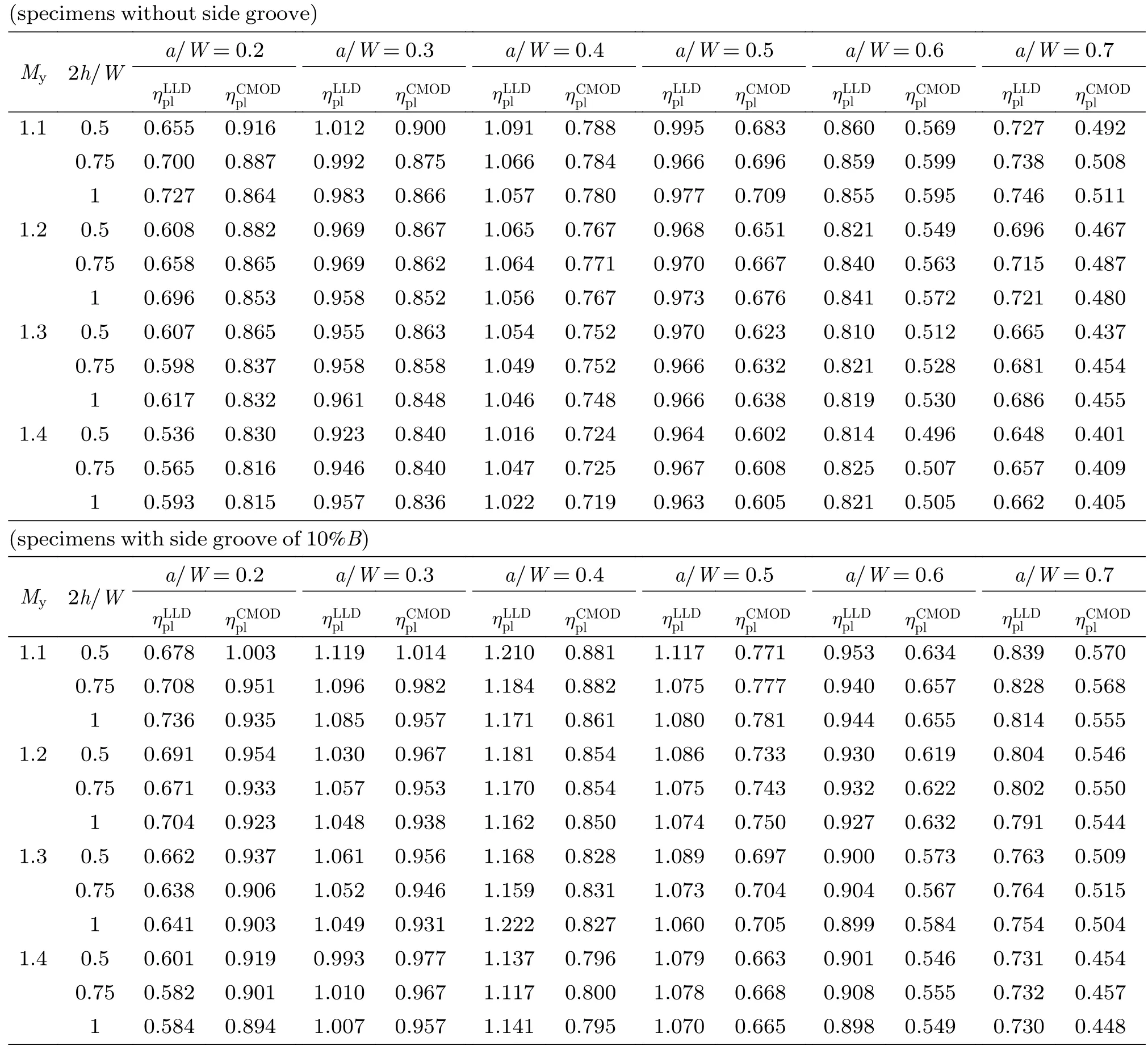
表2 高匹配SENT试样J积分塑性因子计算结果Table 2 Results of J-integral plasticity factor of over-matched SENT specimens

3.4 高匹配J积分塑性因子公式η

为了便于不含侧槽与侧槽深度10%B的高匹配SENT试样断裂韧性测试，采用多项式拟合J积分塑性因子方程。对于高匹配SENT试样，J积分塑性因子是与裂纹长宽比和匹配系数有关的函数，采用四阶多项式进行拟合，即

式中，αi为与匹配系数有关的函数，mij为拟合系数。和的拟合系数分别见表3和表4，该式的有效范围为：0.2≤a/W≤0.7，1.1≤My≤1.4。

表3 拟合方程系数Table 3 The coefficient of fitting equation of

表3 拟合方程系数Table 3 The coefficient of fitting equation of

Specimens without side groove Specimens with side groove of 10%B i = 0 i = 1 i = 2 i = 3 i = 4 i = 0 i = 1 i = 2 i = 3 i = 4 j = 0 –202.99 2 010.1 –6 712.74 9 381.93 –4 739.78 –509.98 4 720.92 –13 944.58 16 477.67 –6 742.73 j = 1 470.81 –4 617.41 15 321.4 –21 258.7 10 664.4 1 203.41 –11 090.20 32 547.88 –38 051.16 15 318.76 j = 2 –362.23 3 523.89 –11 578.2 15 892.97 –7 891.61 –944.68 8 675.05 –25 263.75 29 168.45 –11 519.43 j = 3 91.86 –886.9 2 883.07 –3 908.86 1 917.17 246.15 –2 253.51 6 512.66 –7 422.57 2 871.05

表4 拟合方程系数Table 4 The coefficient of fitting equation of

表4 拟合方程系数Table 4 The coefficient of fitting equation of

Specimens without side groove Specimens with side groove of 10%B i = 0 i = 1 i = 2 i = 3 i = 4 i = 0 i = 1 i = 2 i = 3 i = 4 j = 0 –90.74 818.08 –2 103.14 1 684.51 –108.60 186.00 –2 212.23 9 164.00 –15 669.03 9 353.13 j = 1 217.44 –1 920.57 4 827.33 –3 607.79 –30.37 –480.42 5 719.96 –23 549.13 40 044.10 –23 808.50 j = 2 –170.62 1 490.45 –3 649.46 2 488.90 279.68 413.50 –4 903.29 20 075.79 –33 970.96 20 124.30 j = 3 43.85 –378.19 894.09 –528.90 –155.56 –118.50 1 398.60 –5 693.85 9 585.35 –5 656.29

4 结论

（1）本文基于三维有限元数值分析，研究不同裂纹长宽比（a/W= 0.2～0.7，增量0.1）、焊缝宽度（h= 5，7.5，10 mm）和匹配系数（My=1.1～1.4，增量0.1）下不含侧槽与侧槽深度10%B高匹配SENT试样的J积分塑性因子，通过拟合方法提出对应的J积分塑性因子方程，适用于管道高匹配焊接接头的断裂韧性测试，可提高测试的准确性。

（2）对于不含侧槽SENT试样，ηpLlLD在裂纹长宽比a/W= 0.3时对匹配系数不敏感，其余情况随匹配系数的增加而减小。对于侧槽深度10%B的SENT试样，ηpLlLD在a/W≤ 0.4时对匹配系数不敏感，其余情况随匹配系数的增加而减小。ηpClMOD随匹配系数的增加而减小。

（3）对于高匹配SENT试样，在不同匹配系数下，焊缝宽度对SENT试样的J积分塑性因子影响较小，可以忽略。相同情况下，侧槽深度10%B的高匹配SENT试样J积分塑性因子明显高于不含侧槽SENT试件，测试时应根据试件侧槽情况选择对应的J积分塑性因子方程。