封闭应力方向对巴西圆盘试验影响的数值模拟1)
2022-07-02佟业蒙
王 涛 王 莉 佟业蒙
(北京科技大学土木与资源工程学院,北京 100083)
岩石是由一种或几种形状稳定的矿物组成的固体集合体。岩石在经过建造、构造变形和地表次生变化后,在消除外力和不均匀温度场作用后仍有保留在岩体中的力叫封闭应力[1]。封闭应力的概念是由Müller提出的,之后陈宗基等[2]也指出封闭应力是岩石性状的基本因素,在实际工程中起到重要作用。2000年,安欧[3]用X射线法,以岩体正交异性弹性理论为基础,测得局部区域的封闭应力的大小。2013年,钱七虎等[4]确定岩体的非协调变形会产生自平衡封闭应力,认为微裂纹密度和长度会影响封闭应力。2014年,岳中琦[5]提出封闭应力的具体存在形式是流体包裹体,可以通过测量和计算得到封闭应力的大小。2015年,岳中琦[6]提出封闭在完整岩石中存在微小包裹体,猜想并证明了包裹体具有高压强,这种具有高压强的包裹体不仅能够引起完整岩石内部局部高地应力场的异常,还会在包裹体被破坏时造成局部完整脆性围岩的岩爆现象。2019年,许宏发等[7]和Geng等[8]采用相似模拟技术,利用混凝土和橡胶球分别模拟岩石基体和流体包裹体,利用两种材料的热膨胀系数不同,通过加热实现橡胶颗粒的膨胀,把膨胀产生的力等价于封闭应力,成功通过物理实验测得封闭应力。2020年,Geng等[9]用自行设计的方法测试了不同环境温度下夹杂物产生的封闭应力,通过比较和修正得到了量化封闭应力的经验公式。2019年,杨小彬等[10]根据封闭应力假说建立含应力包裹体的掘进工作面简化力学模型,进而得到岩石封闭应力的理论计算公式。
存在于岩样中的封闭应力是自平衡的,一旦这种平衡被打破,里面的封闭应力就会被释放,因此封闭应力的存在会对地下工程开挖带来严重危害,如在开挖时造成地应力突然卸载,使得岩体在临空面处无法依靠自身强度维持封闭应力的平衡,造成地质灾害,典型的瓦斯突出、煤体喷出等现象可能与局部封闭应力大有关[11-13]。如何确定封闭应力对岩体的影响、减小或消除封闭应力对工程的影响,已成为人们广泛关注的问题[14]。因此,开展岩石封闭应力的研究具有重要的工程和理论意义。
目前,越来越多的学者开始了对岩石封闭应力的研究,包括封闭应力的存在形式、作用机制、测试手段和对岩体宏观力学行为的研究,总体来说还未形成成熟的体系,仍需进一步深入研究[15-17]。为研究封闭应力对岩石力学性能的影响,采用数值模拟技术,在ABAQUS中建立岩石的数值模拟模型,将一定区域的封闭应力等效成一个封闭的包裹体分布在岩石中,在包裹体外部附上封闭应力,对比分析封闭应力方向不同对岩石应力和裂纹扩展的影响。本文提出的数值模拟试验可为后续开展封闭应力对岩石力学性能的影响研究提供参考。
1 计算模型和模型参数
1.1 计算模型
岩石在深部地下经过长期地质作用,在岩体内部形成封闭应力,其对岩石力学特性的影响较大。该封闭应力在岩体内依靠岩体基质来平衡,岩体基质被破坏时就会释放。实际试验时,当岩样取出后封闭应力会慢慢释放,无法长期存留于岩块试样中。鉴于此,许宏发等[7]提出将存在封闭应力的区域等效成矿物固体中的封闭包裹体,如图1所示。文章利用水泥基类材料和丁腈橡胶材料的热膨胀系数不同,用它们分别模拟岩石基体和封闭应力。通过加热使丁腈橡胶膨胀产生应力,以此模拟包裹体中的封闭应力。

图1 简化模型示意图Fig. 1 Schematic diagram of simplified model
理论上,岩体中的包裹体在无外力作用时对外表现为无应力状态,由此推断岩体内存在一个力与封闭应力平衡,因此封闭应力就等价于一个外部作用力附在包裹体上,研究封闭应力对岩体的影响,转化为研究包裹体上一个外力对岩体的影响。本模拟结合包裹体的理论模型和封闭应力平衡机制,在包裹体上施加不同方向的封闭应力,模拟包裹体受力破坏时封闭应力释放对岩体的破坏影响,在包裹体上施加封闭应力,该封闭应力会对岩体局部范围产生影响,在受到外力时,与外力共同作用对岩体产生破坏变形。
为了分析封闭应力方向对巴西圆盘试验结果的影响,设计了5种不同的数值模型:无封闭应力、封闭应力方向与加载方向的夹角α分别为0°,30°,60°,90°,封闭应力施加在包裹体圆周上,不同方向封闭应力作用在包裹体圆周的cohesive单元上,每个方向选取夹角为30°的两个连续cohesive单元,如图2所示。模拟模型尺寸为直径50 mm,厚度25 mm。其中,cohesive单元采用4节点平面COH2D4,岩石基体采用3节点平面应变单元CPE3,有限元模型共划分49 353个三角形单元,如图3所示。采用最大损伤准则,加载方式为控制位移,边界条件为:上下压板设置成刚体,固定下压板,上压板施加z方向的速度边界条件,限制其他方向自由度,加载速率为每步1.5×10–10m。在加载时,圆盘同时受上压盘的压力和圆盘内部的封闭应力的作用。
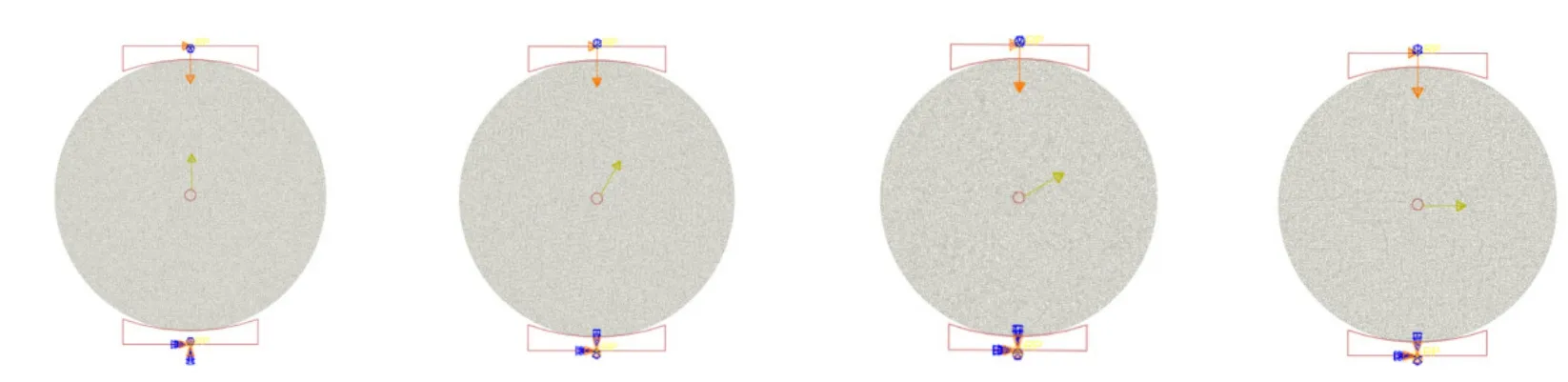
图2 不同方向封闭应力作用下的圆盘试验数值模型Fig. 2 Numerical model of disc test under locked-in stress in different directions

图3 有限元模型及网格划分Fig. 3 Finite element model and meshing
1.2 模型参数
(1)确定封闭应力大小
利用X射线衍射法对石英岩封闭应力进行测量。图4(a)为不同ψ角度下测得的衍射图谱,ψ为衍射晶面法线与试样表面法线之间的夹角,θ为入射线与晶面法线的夹角;图4(b)是图4(a)中153°~154°峰中心位对应的θ值,计算得到直线的斜率M= 0.000 73。
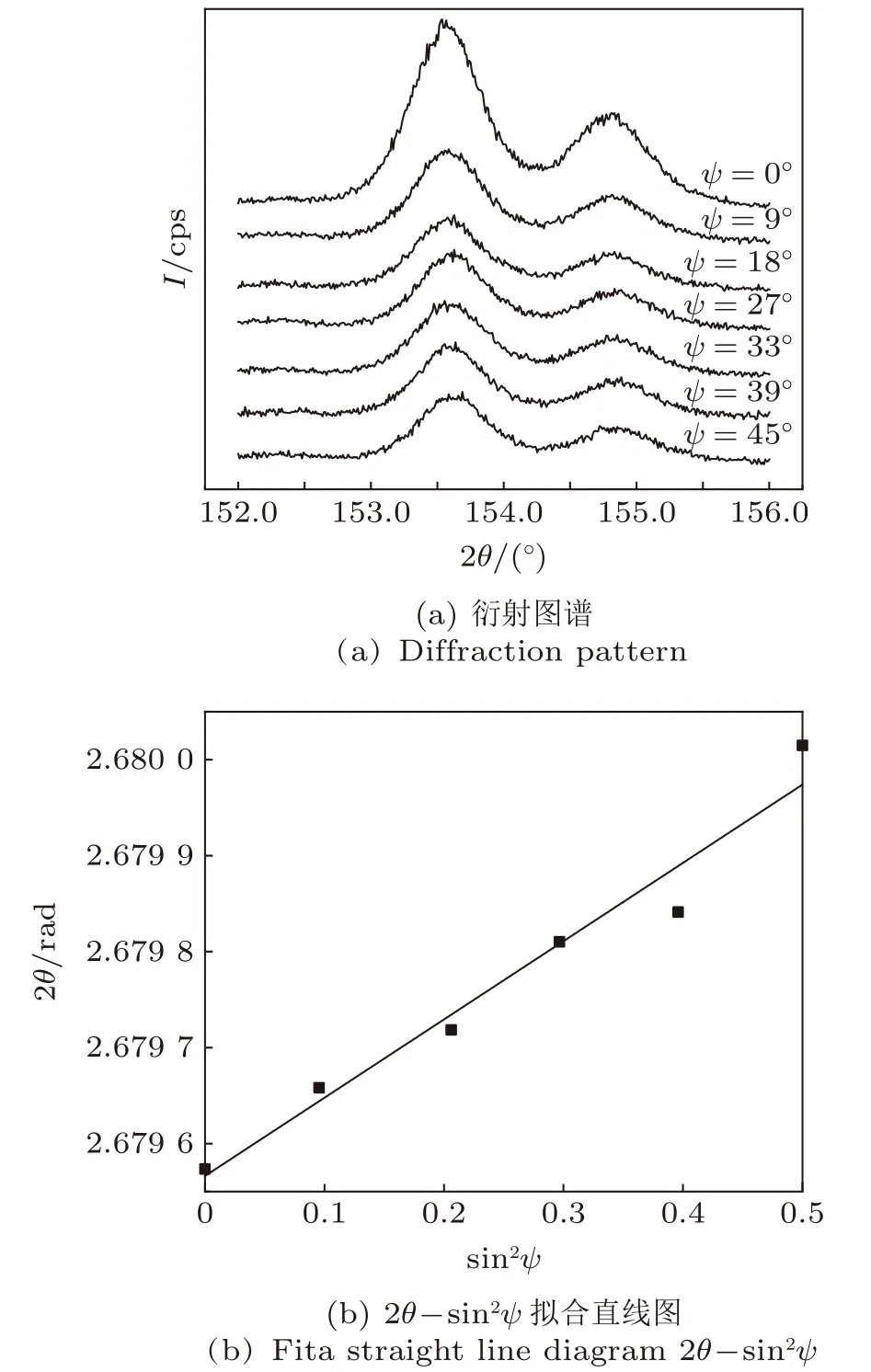
图4 衍射图谱和 2 θ−sin2ψ 拟合直线图Fig. 4 Diffraction pattern and fit a straight line diagram 2θ−sin2ψ
基于平面应力状态假设,根据弹性理论与布拉格定律,推导 s in2ψ法应力计算公式(1)[18],将M= 0.000 73代入式(1),求得封闭应力σr=6.18 MPa。
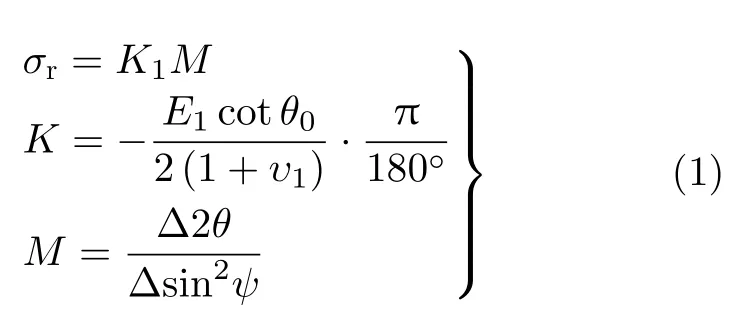
式中,K1为应力系数;E1为矿物晶体某晶面的弹性模量,取E1= 90 GPa;υ1为矿物晶体某晶面的泊松比,取υ1= 0.25;θ0为无应力时的衍射角,θ0取ψ= 0°时对应的弧度。
(2)其他物理力学参数
T为损伤起始应力,取T= 1.3 MPa;GIC为损伤断裂能,取GIC= 1.1 N /mm ;η为粘结系数,取η= 0.006;H为单元厚度,取H= 25 mm;E为杨氏模量,取E= 8 GPa;υ为泊松比,取υ= 0.25;ρ为密度,取ρ= 2×10−9g /cm3;F为抗拉强度,取F= 14 kN。
2 数值模拟结果分析
本文共模拟5种计算方案,其中方案1和方案2为无、有封闭应力的对比实验,方案2~5是封闭应力方向不同的平行实验。五种方案采用加载方式为控制位移,模拟无封闭应力和封闭应力方向α= 0°,30°,60°,90°时岩石加载过程的应力变化情况,对比分析改变封闭应力的方向对岩石应力分布的影响以及5种情况下裂纹起始位置及裂纹延展的情况,分析存在封闭应力岩石的破裂力学特性及裂纹带演化过程。
2.1 应力分析
2.1.1 有无封闭应力的影响(方案1和方案2)
图5和图6分别为方案1(无封闭应力)和方案2(有封闭应力且α= 0°)不同加载时间的应力变化云图。每种方案取3种状态云图,T1状态是圆盘等效应力最大时的应力分布图,T2是圆盘等效应力突降时的应力分布图,T3是裂纹即将产生阶段应力分布图。根据图5和图6的应力分布图可得如下结论。
(1)两种方案下应力场变化趋势大致相同,高应力区域主要集中在受压圆盘的两端,向中间逐渐减小,随着加载的进行圆盘上的应力逐渐增大。图5可以看出,在T1状态云图中施加封闭应力的位置无明显的应力变化,圆盘其他部位的应力均表现为上下应力大,逐渐向中间减小的趋势,而图6的T1中间出现明显的应力集中现象。
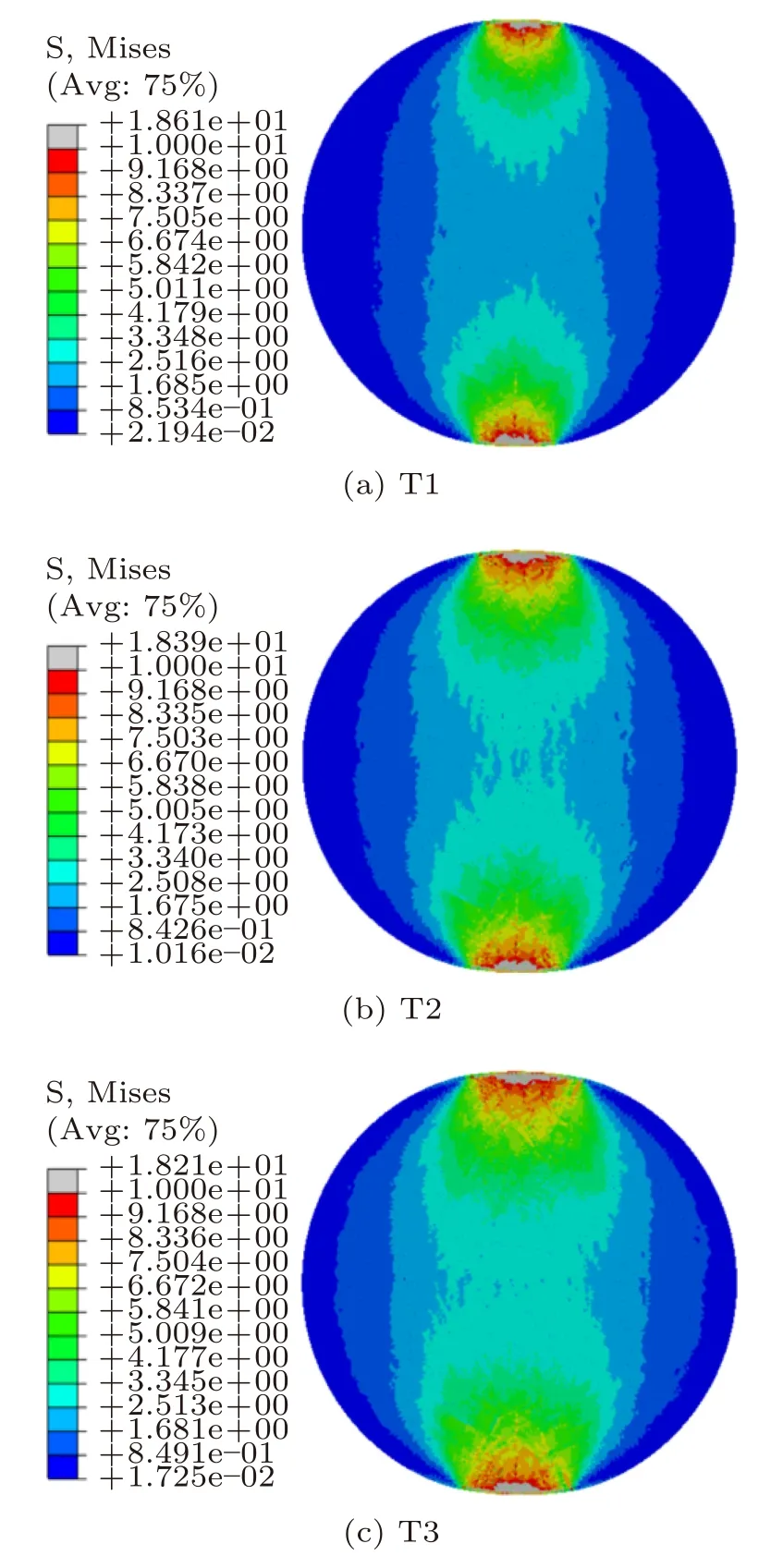
图5 方案1的应力云图分布Fig. 5 The stress cloud distribution of scheme 1
(2)从图6中虚线椭圆圈出的位置可以看出,随着加载的进行,圆盘中间出现小范围的应力集中现象,即施加封闭应力的部位出现局部应力变化明显高于未施加封闭应力的区域,封闭应力变化区域随加载的进行慢慢向上扩展,最终在中间出现局部应力小于周围应力的区域。
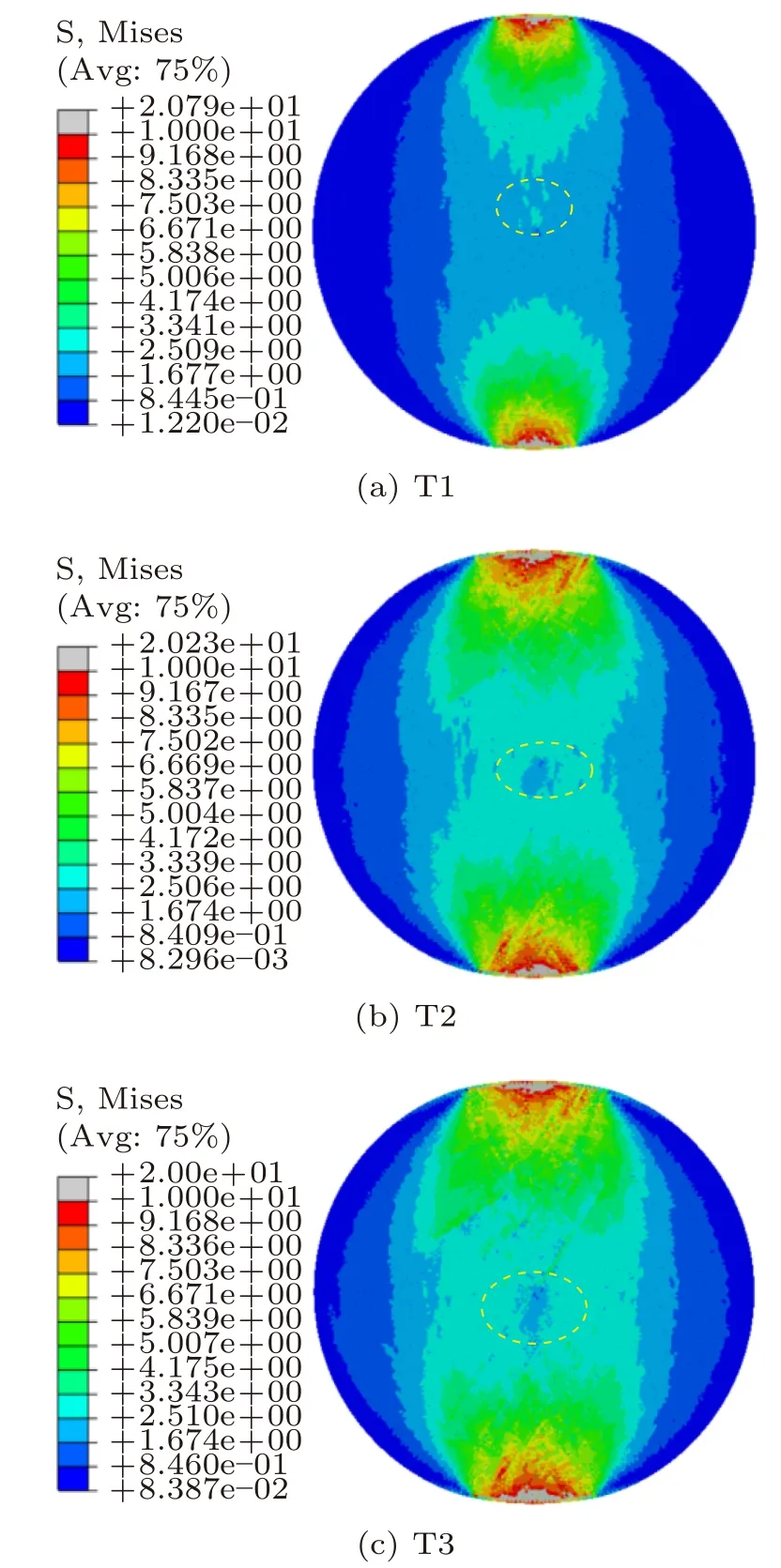
图6 方案2的应力云图分布Fig. 6 The stress cloud distribution of scheme 2
(3)根据方案1和方案2的等效应力的变化,可以看出两种方案均是先增加后减小,其中方案1的最大等效应力值为18.61 MPa,方案2的最大等效应力值为20.79 MPa,对比得出,有平行加载方向的封闭应力存在时,最大等效应力值有所增大。
2.1.2 不同方向封闭应力的影响
图7~图9是方案3~5的不同加载时间对应的应力变化云图。每种方案取3种状态云图,T1状态是圆盘等效应力最大时的应力分布图,T2是圆盘等效应力突降时的应力分布图,T3是裂纹即将产生阶段应力分布图。根据图6~图9可得如下结论。
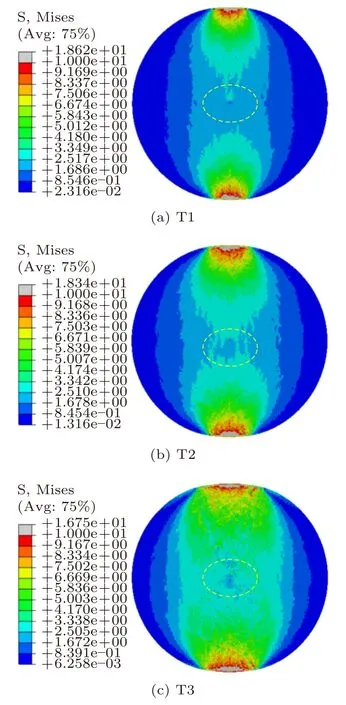
图7 方案3的应力云图分布Fig. 7 The stress cloud distribution of scheme 3
(1)对比图6~图9中虚线椭圆圈出的区域,可以看出封闭应力的角度不同对应的应力云图也各不相同。对比4种方案中T1状态下的等效应力最大值,可以看出方案2最大,达到20.79 MPa;方案3、方案4、方案5的基本持平,等效应力最大值在18.31~18.62 MPa之间。

图9 方案5的应力云图分布Fig. 9 The stress cloud distribution of scheme 5
(2)从T2的应力云图可以看出方案2(α=0°)的应力值的增长速度明显快于其他方案,从方案5中T1~T3的应力云图变化推断,当封闭应力方向垂直加载方向时,在初始裂纹出现前,对应力云图竖向的变化基本无影响,仅对横向应力变化产生影响。
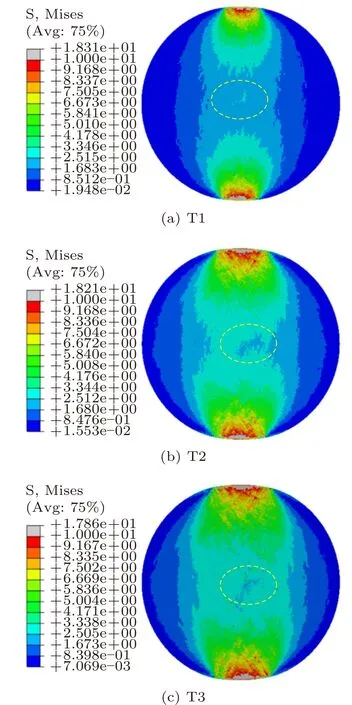
图8 方案4的应力云图分布Fig. 8 The stress cloud distribution of scheme 4
2.2 劈裂破坏形态变化
图10为方案1~5圆盘开裂过程图,其中T4是初始裂纹产生时刻,T5是圆盘裂纹贯通时刻。根据图10可得如下结论。
(1)方案1和方案2的T4时刻均是圆盘中心起裂后,众多微裂纹汇聚成裂纹带向圆盘上、下两端扩展,最终形成贯穿整个圆盘的裂纹带。不同的是方案2的中间出现许多岩石碎屑,且相较于方案1裂纹带中出现的倾斜短裂纹的开裂程度更大。
(2)由图10可以发现,方案3~5中倾斜裂纹出现在开裂初期,三者圆盘均未出现中心起裂,由此可见,当封闭应力的方向与加载方向的夹角大于0°时,圆盘破裂受倾斜裂纹影响较大,完全破裂形成的裂纹带也各不相同。

图10 无封闭应力和不同方向封闭应力作用下岩石劈裂破坏图Fig. 10 Diagram of rock splitting failure under the action of unlocked in stress and locked in stress in different directions
(3)对比方案2~5的T5时刻可以发现,封闭应力的存在使得圆盘中间应力集中,造成圆盘中间裂纹开口变大,从而形成方案3~5中的倾斜短裂纹也延展成裂纹带,相较于方案2裂纹带有明显的曲折,岩石破裂面周围的碎屑也明显变多。
本节讨论了有无封闭应力和封闭应力方向对岩石动态裂纹扩展机制的影响。在数值模拟试验中,当T=0 时,此时无外载荷作用,含封闭应力的岩石处于自平衡状态,含封闭应力的包裹体与一定区域岩石基体自相平衡;当T> 0 时,圆盘上下受压力,施加轴向应力接近或等于岩石最大抗拉强度时,完整脆性岩石就会破裂、崩飞。本试验岩石破坏过程,满足平衡方程和协调方程,符合弹性、弹塑性力学理论规律。模拟结果表明由于封闭应力的存在,加重了圆盘破裂的程度,影响了圆盘裂纹发展的方向,特别是加速了倾斜裂纹的发展,造成圆盘裂纹带形状的改变。
3 结论
本文基于有限元分析软件建立有无封闭应力两种情况下的巴西圆盘破裂分析模型,并讨论了不同角度封闭应力存在对岩石力学性能的影响,分析了圆盘开裂前的应力变化和开裂后圆盘的破坏特征,试验研究对岩石封闭应力的研究提供了一种可行性思路。得到如下结论。
(1)对比分析有无封闭应力的应力云图可得知,当存在封闭应力时,圆盘中间将出现小范围的应力集中现象,即施加封闭应力的部位出现局部应力变化明显高于未施加封闭应力的区域,封闭应力变化区域随加载的进行慢慢向上扩展,最终在中间出现局部应力小于周围应力的区域。
(2)封闭应力不同角度对应的应力云图也各不相同,当封闭应力与加载方向夹角为0°时,圆盘上最大等效应力值达到20.79 MPa,约比其他方案的最大等效应力值高出2.20 MPa,因此可得出封闭应力与加载方向的夹角为0°时,可增大岩石的最大等效应力值。
(3)根据裂纹起始位置和裂纹延展示意图得知,无封闭应力和封闭应力与加载方向夹角为0°时,圆盘中心起裂,而封闭应力与加载方向夹角为30°,60°,90°时,倾斜裂纹出现在初始破裂阶段,而造成方案3~5中的倾斜短裂纹也延展成裂纹带,圆盘均未中心起裂;封闭应力的存在使得圆盘中间应力集中,造成圆盘中间裂纹开口变大,圆盘完全破裂时破裂面周围的碎屑明显变多。
