Kustaanheimo–Stiefel变量与二体问题的正规化

刘延柱

(上海交通大学工程力学系，上海 200240)

1 四元数与Kustaanheimo–Stiefel变量

1843年爱尔兰数学家哈密顿（Hamilton,W.R.）创造了四元数，1845年英国数学家凯莱（Cayley, A.）将法国数学家罗德里格（Rodrigues,B.O.）利用半角公式创造的描述刚体姿态的4个参数表达为四元数形式，使四元数成为处理刚体有限转动姿态变化的数学工具[1]。

经典力学中的二体问题有周知的开普勒运动解析解，但存在引力中心处的奇异性，且不适用于有非中心引力出现时的受扰情形[2]。受扰二体运动问题是有推力存在时航天器轨道运动的基础理论，有重要的实际意义。1906年意大利数学家列维–奇维塔（Levi–Civita, T.） 提出一种变换能使受扰的平面二体问题的奇异性消除，转换为线性微分方程求解，称为二体问题的正规化（regularization）[3]。1964年 库 斯 坦 海 莫（Kustaanheimo, P.）和斯提费（Stiefel, E.）将Levi–Civita变换扩展至三维空间。他们提出用4个Kustaanheimo–Stiefel变量（以下简称K–S变量） 描述点在三维空间内的位置，能使受扰二体问题的非线性三维模型实现正规化[4]。K–S 变量的提出比四元数晚了一个世纪，所定义的4个参数也不同于四元数，但与四元数有着密切的联系和类似的功能。K–S变量并非凭空产生，而是从四元数直接转换形成。本文叙述此转换过程，以及将K–S 变换应用于二体问题正规化的数学推导过程。

2 四元数如何表达笛卡尔坐标

四元数是4个标量λk(k=0,1,2,3) 的组合，或视为标量λ0和矢量λ=λ1i+λ2j+λ3k的组合，表示为=λ0+λ。四元数的乘法运算遵循特殊的规则，可利用矩阵运算实现。将四元数组成列阵和方阵，即

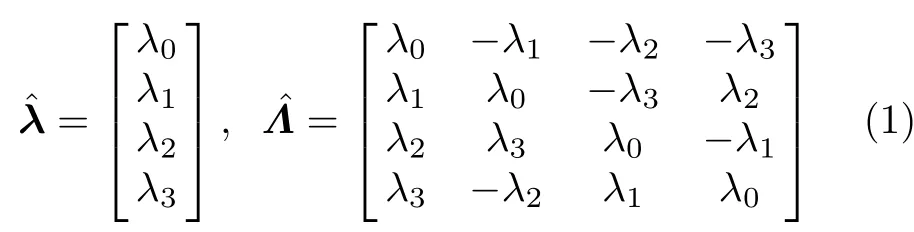
用空心圆点o表示四元数的乘法运算，将四元数方阵与另一四元数列阵相乘，即得到二者的乘积。将基矢量i视为λ0=λ2=λ3=0 ，λ1=1的特殊四元数，令与相乘，得到

令四元数中的矢量λ变号，称为原四元数的 共 轭 四 元 数，记 作=λ0−λ。令与相乘，得到

乘积列阵由一个零元素和3个非零元素组成。将式（3）中方阵和列阵的第1行转移为第4行，再将方阵的第1列转移为第4列，则乘积结果变为

式（4）与式（3）的区别仅改变了乘积列阵中元素的顺序，使零元素从第1行移至第4行。如令其中3个非零元素与三维空间的笛卡尔坐标x,y,z相等，即可利用四元数表达点在三维空间中的位置

3 K–S变量与K–S变换

将式（4）左侧列阵的各元素依次改用uk(k=1,2,3,4) 表示，令

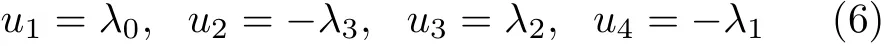
将uk(k=1,2,3,4) 称为K–S变量，令其代替式（4）左侧方阵中的各个元素，得到的方阵记作L(u) ，所排成的列阵记作u，即

L(u) 与u的乘积由笛卡尔坐标x,y,z及零元素构成，记作r，即

其中

则x，y，z组成的三维向量被转换为四维向量u。将L(u) 的第4行元素改变符号，在不影响式（8）的乘积情况下，使得第1列与列阵u相同，形式更为整齐。改造后的方阵L(u) 定义为K–S矩阵。

利用四维K–S变量表达点在三维空间中的笛卡尔坐标称为K–S变换。

4 K–S矩阵的性质

K–S矩阵有以下特殊性质。

（1）K–S矩阵的第1列等于列阵u。

（2）正交性

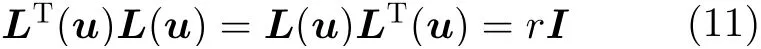
其中I为单位阵，r为K–S变量的范数，与矢径r=xi+yj+zk的模相等

（3）K–S矩阵的微分等于各元素微分后的矩阵

（4）互易性

若四维函数u和w满足双线性条件

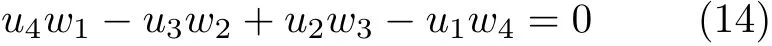
则函数u和w存在互易性

5 二体问题的正规化

讨论卫星与地球组成的二体问题，在动力学方程内增加单位质量的扰动力p，写作

其中µ为地球的引力参数，r为二体的距离。扰动力p以四维向量表示为p=(pxpypz0)T。无扰动时p=0 ，存在能量积分

因椭圆形轨道的积分常数为负值，增加负号后使常数E为正值。

将时间变量t置换为新自变量s，满足

将式（8）和式（12）表示的r和r变换为K–S变量，计算其对s的导数。以撇号作为对s的导数符号，利用K–S变量u和u′的互易性（15），导出

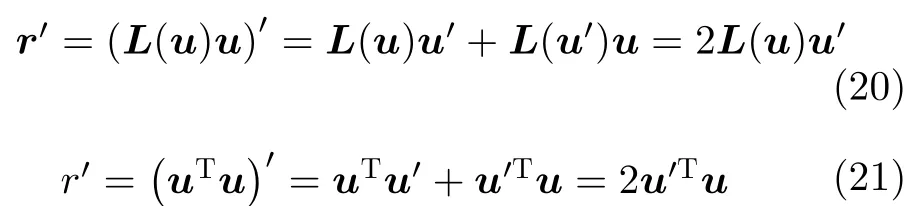
上述u与u′的互易性应在满足双线性条件（14）的前提下成立，证明过程从略。令r对t求导计算卫星的速度v。以点号作为对t的导数符号，列出

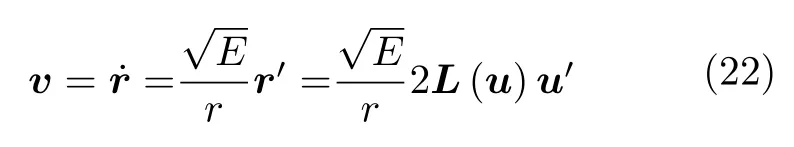
利用正交性（11），导出

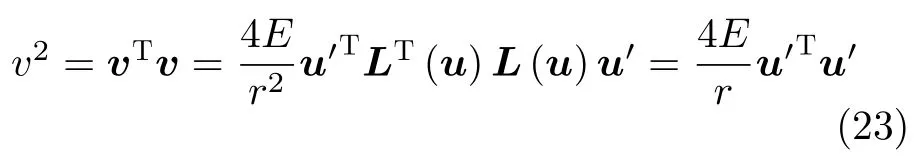
代入能量积分（18），得到

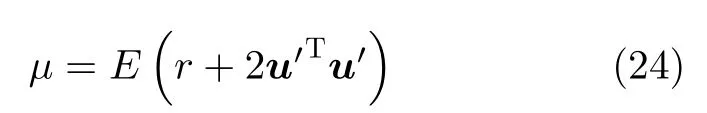
有扰动存在但扰动力p远小于引力时，可近似使用无扰状态的能量积分计算该瞬时的密切开普勒轨道，轨道参数视为时间t的慢变函数。机械能−E对t的变化率−等于扰动力p的功率。计算−E对s的导数，将式（22）代入，得到

令式（22）再对t求导计算卫星的加速度，其中r′以式（21）代入，得到

令各项左乘LT(u) ，利用式（11）和式（16）简化，得到

令二体运动方程（17）左乘r3LT(u) ，将式（27）代入，得到

将其中的参数µ和E′以式（24）和（25）代入，整理后得到正规化的二体运动方程

其中

除上述二体问题以外，K–S变换也可用于其他引力中心存在奇异性的正规化问题，例如限制性三体问题[5]。