关注数学本质，提升思考能力

张燕婷

摘 要：在小学数学概念教学中关注数学本质，怎样才能抓住数学本质？史学观点与应用价值是两个重要的思考方向，结合“圆的认识”的教学案例，对教材进行合理的处理，从学生的切实需求出发，提升小学生数学思考能力。

关键词：概念教学;数学本质;圆的认识

中图分类号：G623.5   文献标识码：A   文章编号：1673-8918（2022）21-0111-04

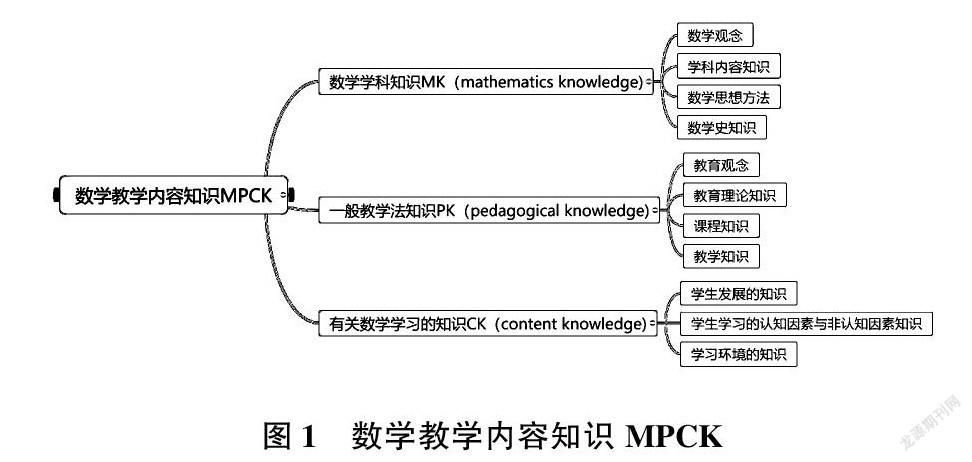
小学有许多内容都需要从数学本质的揭示上进行梳理，仅就一些教育理念进行教学设计是走不远的。细品张奠宙先生的《小学数学教材中的大道理——核心概念的理解与呈现》一书，近几年，提倡MPCK（Mathematics Pedagogical Content Knowledge，簡称MPCK，意为数学内容的教学知识）研究（图1），教师要在教学内容的理解上下功夫，真正关注数学本质，提升小学生数学思考能力，才是有的放矢的决策。

苏教版五下《数学》教材安排3页认识圆，先从实际生活中找到圆，再启发思考圆与之前直线图形的相同点和不同点。然后想办法画一个圆，可以是现成的小圆片，也可以利用圆的特质来画圆，或者是直接使用画圆工具——圆规，在画圆的实践过程中再次深化对圆的概念的认识。以圆规画的圆为例，介绍了圆心、半径、直径。启发学生思考：在用一个圆内，有多少条半径，多少条直径？直径的长度和半径的长度有什么关系？在折一折、画一画、比一比的过程中，说说你的发现。

人教版六上《数学》2页教材中，先从自然界、人类生活中找到圆的存在。再启发学生画圆，可以是现成的圆，也可以直接利用画圆工具。用圆规画圆时，圆心找到了，半径也知道了，直径就跟着定义出来了。通过折一折、画一画、量一量的操作过程，继续探索圆心、半径、直径之间的关系。

北师大版六上《数学》2页教材中，从套圈的游戏体验入手，感知定点、定长，这样套圈的站位比较公平。然后也让学生用自己的方式画圆。只呈现从定义出发的画圆，可以是利用拇指和食指撑开，也可以是找一根固定长度的线段，最后还是出现了画圆工具——圆规，并启发学生思考，画圆时应注意什么？直接利用圆规画的圆，定义圆心、半径以及直径，并探究半径之间、直径之间、半径与直径之间有什么关系。再寻找圆的大小与什么有关，圆的位置与什么有关，一个概念的内涵越大越丰富，则其对应外延反而越小。核心问题的提问直接限制了思考的发散性。

圆是生活中常见的几何图形。儿童早在低幼时期就对圆的认识有了初步的经验。对比以上3个版本的教材，我们可以发现，在小学数学界，对圆的概念的定义是模糊的。它们依然停留在蒙眬的圆的直觉里，没有界定：“什么是圆。”3个版本都是基于圆规画的圆来定义圆心、半径、直径。六年级的学生已经接近少年时期，完全有能力弄清“圆”真正的几何学定义。张奠宙先生建议：我们不妨在使用圆规画圆的活动之后顺势提出如下的定义：让线段OA绕着它的一个端点O旋转一周，我们把另一个端点A所画出的曲线叫作圆，点O称为圆心，线段OA称为半径。这样的定义不过是圆规画圆过程的数学描述，其中只用了小学里已有的“线段”“旋转”等术语，避免使用中学里才出现的“集合”“轨迹”等名词，六年级学生是完全能够接受的。阅读此文后，感受到张先生在概念教学中数学本质上的重视，体会到高观点下的初等数学，茅塞顿开，对原教学设计进行再加工，呈现相关的课堂设计（图2）。

一、 巧用素材，凸显概念本质

课前，提出问题，启发思考：除了圆心、半径、直径，你还想知道哪些圆的知识？收集学生的问题，进行有效的整理和组织，解答学生对圆的切实需求。

设计意图：数学源于生活不应该只停留在口号上，努力让学生感受生活中的数学。关注学生的需求，对圆的认识这一节概念课的执教是有帮助的。从学生的反馈可以知道不少学生已经超前学习，比如弦、圆周角等，这部分内容属于初中知识，可以适当回应但不展开，对半径、直径之间的关系以及割圆术可以展开，对圆的宏观认识是有帮助的，还可以渗透数学思想方法（化曲为直思想等）。

问题：套圈比赛要求站在离目标1米远的距离，怎么站？请说明你的理由。

活动过程：

先小组讨论，给学生思考时间，再实践游戏。

邀请一个学生站，并提醒：他离目标的距离是1米。再邀请一个学生，还能站在哪？若干学生尝试站好位置，再套圈。

师：以这个目标为定点，以1米为定长。如果把每一个学生看成一个点，点点成线，像这样绕着这个定点O旋转一周，我们把另一个点所画出的曲线叫作圆（circle）。圆上任意一点到定点的距离都是定长。

问题：点和圆的位置关系有哪些？（圆内;圆上;圆外）

设计意图：因为圆在生活中随处可见，所以研究圆的时候，学习材料可以从生活中来，研究得到的结论可以反过来应用于生活。在教学中，要合理用好生活素材，把这些素材作为引发学生探究、促进学生思考、加深学生感悟的有效载体。以学生站位动态生成的圆的形象，可以很直观地认识什么是圆，也弥补了小学数学教材中对圆的概念的模糊性处理的遗憾。利用学生的套圈结果（学生站在圆周上，套圈散落在圆内或者圆外等），可以很好地渗透教学内容：点和圆的位置关系，沟通零维空间与二维空间之间的联系。

二、 选用史料，彰显数学文化

圆规的发明最早可追溯至中国夏朝，《史记·夏本纪》载大禹治水“左准绳，右规矩”，公元前15世纪的甲骨文中，已有规、矩二字，当时称为“规”，即今日的圆规。早在两千多年前，我国古代就有了关于圆的精确记载。墨子在他的著作《墨经》中这样描述：“圆，一中同长也。”墨子关于圆的定义与欧几里得几何学中圆的定义完全一致。我国古代的这一发现要比西方整整早一千多年。

设计意图：为了丰富学生在数学史方面的知识，通过课件介绍了圆规、圆的一些历史材料，特别指出了我国古代数学家墨子在这方面的伟大成就。让学生从数学发展史的角度了解圆，有助于学生建立动态的数学观。

三、 操作实践，体验圆的形成

问题：在同一个圆内，半径与半径之间、直径与直径之间、半径与直径之间有什么关系？（可以从数量、长度等方面进行比较）

设计意图：探究同圆或等圆中，半径与直径之间的关系，沟通一维空间（线段）与二维空间（圆）之间的联系。长度是可测量的，是有限空间的，可以进行比较。通过测量，学生很容易发现：在同一个圆内，半径、直径的长度都是相等的;直径的长度是半径的两倍。但是在数量上，同一个圆内的半径有无数条，直径也有无数条。这一点，部分聪明的学生会出现反向迁移，觉得在同一个圆内，半径的数量是直径的2倍，因为每一条直径都对应分解成两条半径。教师应知道这里的数量是不可测量的，是数不清的，属于无限空间的，不可以直接进行比较。真的要比较的话，就要引入新的比较对象——基数（无限空间的测量方式）。

四、 运用比较，构建网络体系

问题：这样的位置除了圆上的点，还有吗？说说你的想法。

启发学生脱离二维平面空间的束缚，探索三维立体空间——球。

教师直接站在目标的正上方，调整距离到1米，然后“百套百中”。

师：这个位置可以吗？满足到定点距离是1米的要求吗？

师：还有吗？既可以悬在空中，还可以深入地下。实际生活的局限，有些位置站不到。但在数学上，这样的位置是存在的。古人云：在空间内，一中同长谓之球（solid sphere）。

设计意图：沟通二维空间（圆）与三维空间（球）之间的联系。学生从现实体验的事物中学习数学和理解数学，可以借助信息化技术，展示三维空间的球。学生眼中的圆也就不再是简单的、冷冰冰的数学概念，而是富有情感、贴近生活、具有活力的科学认识产物。它还可以穿越空间，到三维空间变成球。

师：我们之前认识了直线图形——长方形、正方形、三角形、平行四边形之后，根据生活需要，我们还要会求它們的周长和面积。今天，我们认识了圆，那么圆的周长和面积需要求吗？哪些地方可能遇到这样的困惑？如果需要求圆的周长和面积，怎么求？你能想到什么方法解决它？

设计意图：沟通二维空间直线图形（长方形、正方形、三角形等）与二维空间曲线图形（圆）之间的联系。激发学生对圆的周长、面积的探索欲。同类量之间的比较，更容易正向迁移，也为之后化曲为直思想、等积变形思想、极限思想等数学思想方法的使用埋下伏笔。

五、 设计作业，巧妙收获评价

课后：（非原创）小明想给家中圆形餐桌换上一张新的桌布（桌布的大小与餐桌大小一样）。小明已经测量了下面3组数据：①桌布对折后折痕长2米;②用卷尺测量餐桌边缘一周长是6.28米;③桌布对折两次后折痕长1米;如果你是小明，你会根据哪一个数据给桌子换新的桌布？并说明你的理由。

设计意图：数学是源于生活又高于生活的。既然学生在日常生活中随处可见圆，那么就会产生很多对圆的思考，基于学生的困惑而展开的教学是有效的。课前、课中教师用问卷星小软件发布了以上的作业，尊重学生的好奇心，再结合实际生活，挖掘生活中的数学应用。

数学课程应落实立德树人的根本任务，致力于实现义务教育阶段的培养目标，面向全体学生，适应学生个性发展的需要，使得：人人都能获得良好的数学教育，不同的人在数学上得到不同的发展。这个练习是在学生学习圆的面积之后布置的，有43.08%的学生选择了2米，有33.85%的学生选择了都可以。仔细查看，不难看出：学生的思考受限了，他们只考虑到眼前，而没有考虑到整体。只要是直接或者间接得出圆的半径，这样就可以求圆的面积。在日常教学中，不应该让学生盲目机械地做题，沦为做题的工具人，应该让他们对题目有思考，而不是就题解题。

数学是每一个孩子从求学开始都必须要学习的主科，它教给孩子的不应只是冰冷的数学知识，更重要的是要教给孩子用数学的眼光看待问题、用数学的思想去思考问题。数学概念是小学数学知识的重要组成部分，数学概念好比是学生建构数学知识大厦的一砖一瓦，离开了数学概念，数学知识大厦好比是无本之木、无源之水。小学数学教材里的数学知识多数是不严密的，教师应当知道它们的逻辑结构，包括公理化的处理方法，领会现代数学的思想，能够比较准确地把握数学本质。怎样才能抓住数学本质？史学观点与应用价值是两个重要的思考方向，循着这两个方向，容易厘清知识的源与流。

在中国古代，就有无数的先辈对数学进行了先导研究，经过大量的理论研究和实践探索编写了一些著名的数学专著，为人类文明的发展做出了重大贡献，主要是《九章算术》《周髀算经》《海岛算经》《张丘建算经》和《缉古算经》等五部。①九章算术，它在数学上有独到成就，最早提到了分数问题，也首先记录了盈不足等问题。《方程》章，在世界数学史上首次阐述了负数及其加减运算法则。它的出现，标志中国古代数学形成了一个完整的体系。②周髀算经，它在数学上的主要成就是介绍了勾股定理。③海岛算经，是中国学者编撰的最早一部测量数学著作，为地图学提供了数学基础。它被称为实用三角法的启蒙著作，只是未涉及三角学中的正余弦概念。书中问题，都是利用两次或多次测量、观望所得数据，进而推算目标的广、远、高、深。④张丘建算经，该书突出的成就是最大公约数与最小公倍数的计算，各种等差数列问题的解决，及某些不定方程问题求解等。百鸡问题是《张丘建算经》中的一个著名数学问题。⑤缉古算经，为中国现存最早解决三次方程的著作，详细叙述建立方程的理论依据和具体程序，解题方法言简意赅、通俗易懂。对以上几本古代数学专著略有研究的话，对学生形成宏观的数学观有帮助，数学知识的推进很多时候是因为现实生活的需求，古人对数学的研究更大程度上推动了当时生产活动，在实际教学中，适当地讲解一些数学趣闻，数学史话，体会数学在人类发展史上的作用。

教师只有把握了数学本质，教学中才能做到“精中求简”。唯有做好“精中求简”的研究，才能真正提高教学质量与效果，也唯有这样，才能使得基础数学易学、好懂、能懂、会用，从而真正减轻学生的负担，在“双减”的同时“提质”。

参考文献：

[1]张奠宙.更多地关注数学本质与细节处理：以圆的定义为例[J].小学教学，2014（8）：8-9.

[2]姜荣富.返璞归真 平易近人：读张奠宙教授的文章有感[J].小学教学，2016（8）：8-10.

[3]陈丽萍.数学教材中的中国古典数学教学研究[D].大连：辽宁师范大学，2020.