基于实测数据的复合材料层合板热导率预测方法
2022-07-01张肖肖张赐宝秦强丛琳华
张肖肖,张赐宝,秦强,丛琳华
中国飞机强度研究所,陕西 西安 710065
随着复合材料(复材)在飞机制造领域的使用日益广泛[1-2],在考虑复材传热性能进行热应力分析或者环控系统等相关设计时需要复材不同温度下的热导率数据。由于复合材料的各向异性和可设计性,即使对于相同基体、相同纤维、相同纤维体积分数组成的复合材料,由于其铺层顺序不同,导致其热导率数据存在差异,并且在X向、Y向和Z向呈现出显著差别。通过试验测试可以获取复材试样不同方向的热导率,但必须制造测试试样,此外存在测试周期较长、测试对硬件条件依赖度高等问题,对于采用新的铺层顺序设计的层合板,又需要重新制造试样进行测试,不能满足结构设计中的缩短周期需求,无法支撑复材结构优化、环控系统设计等的快速评估迭代,因此需要研究复合材料层合板不同方向热导率的预测方法。
目前,有多种碳纤维复合材料面内和厚度方向热导率计算模型[3-5]。李仕通[3]梳理了在不同铺层角度情况下碳纤维复合材料(CFRP)单向铺层面内和厚度方向热导率计算模型及测试方法,分析了不同树脂体系和增强体,以及工艺方法等因素对CFRP热导率的影响。钟轶峰[4]采用单胞变分渐近均匀化方法构建了一种新的细观力学模型来预测非均质复合材料的有效热导率,该模型并不适用于由单向铺层组成的复材层合板。李仕通[5]还研究了铺层角度对三种复材层合板导热性能的影响规律,采用解析方法、有限元方法,以及数值拟合方法建立了碳纤维复合材料导热性能预测模型,并与试验数据进行了验证分析,其研究的是单向铺层并非混杂铺层。以上研究多针对单向铺层预测,并且普遍依赖基体和纤维的热导率数据,因此在使用前需要先获取基体、纤维的相关数据,不能直接以一般混杂铺层试样的实测数据分析出单向铺层热导率,更难以应用于混杂铺层热导率的预测。参考文献[6]在对复材蒙皮与内饰组合结构热阻预测过程中,将特定混杂铺层的复材Z向热导率实测值进行拟合来预测不同温度下的热导率,并未对Z向热导率与各角度铺层之间的关系进行探讨。目前也有采用有限元法来预测复合材料有效热导率的相关研究[7-11]。例如,程磊[7]建立以不同体积球形颗粒填充型复合材料模型,预测了相应颗粒体积填充量下的有效热导率,该模型不能用于预测纤维增强层合板的热导率预测。左可军[9]研究了平纹编织结构的三维纤维随机模型,该模型可给出三维编织复合材料的等效热导率,并不对X、Y、Z向进行区分。有限元法预测则对分析模型的准确性要求更高,十分依赖使用者的经验,不易操作,适用于计算颗粒增强型、编织体型等微观结构更为复杂的复合材料热导率。目前缺少能够直接根据一般混杂铺层层合板热导率实测数据对未测试的混杂铺层试样在X、Y和Z向热导率进行预测的方法。
本文基于稳态传热理论,建立复材层合板Z向、X/Y向热导率与单一角度铺层热导率的关系式,按照线性方程组求解和统计思想,从少量实测热导率数据中计算得到单一角度铺层的热导率平均值,再根据该关系式来计算待测试样的热导率预测值,最后通过对比实测值与预测值的相对误差,分析本文预测方法的正确性。
1 Z向热导率预测方法
Z向传热串联模型如图1所示,Z向热导率预测方法的计算思路如图2 所示。对于每一个热导率实测数据Ke,其对应试样的等效热阻

图1 Z向传热串联模型Fig.1 Series‐wound thermal conduction model in Z‐orientation
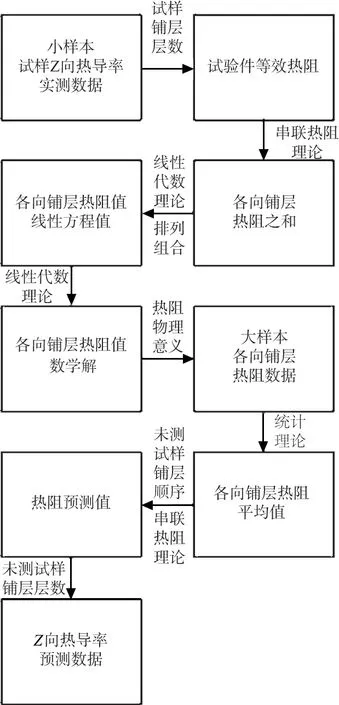
图2 Z向热导率预测方法示意图Fig.2 Scheme of the prediction method for thermal conductivity in Z‐orientation

式中:d为复材试样厚度。由于在激光导热仪(LFA)的激光脉冲作用下试样的温升幅度很小,可以认为各铺层的温度相同,因此相同角度铺层的热导率相同,同时由于各铺层厚度相同可以得到相同角度铺层的热阻相同。根据串联热阻理论,可以得到试验件等效热阻等于各向铺层的热阻之和
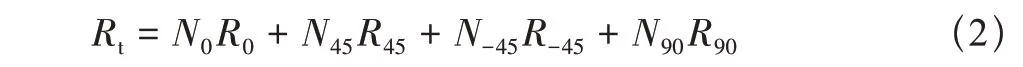
式中:下标代表单一铺层角度;Rt为复材试样的等效热阻;N为试样中当前角度铺层的总层数;R为相应角度铺层的热阻,式(2)消去单层厚度后认为R=K-1,K为该角度铺层的热导率,此时Rt=Nt/Ke,Nt为试样铺层层数。
对于每一个混杂铺层试样的实测数据,都可以根据式(2)得到一个以R0、R45、R-45、R90为未知数的四元一次方程。求解4个未知数至少需要4个方程联立,从同一温度下各个试样实测数据对应的四元一次方程中进行任意组合,这样的方程组一共有C4n个(n为当前温度下实测数据的个数),每一组方程组均为以下形式
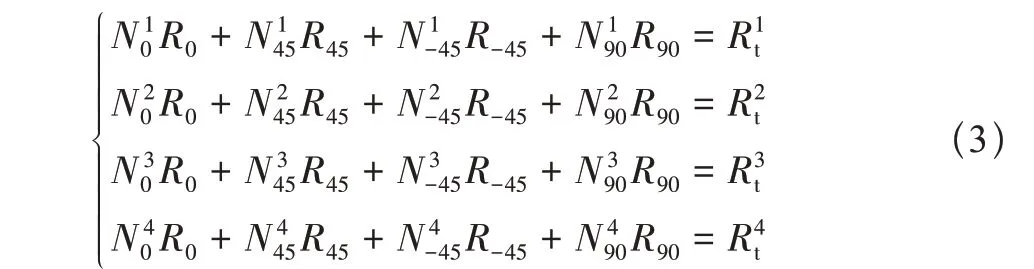
式中:上标代表不同样本的编号。
根据线性代数理论,线性方程组AX=B的解为X=A-1B,前提是矩阵A满秩,每求解一组式(3)表示的方程组便得到一组R0、R45、R-45、R90的值。求解所有存在数学解的方程组,考虑到热阻均大于0,再筛选出满足物理意义的数学解,形成大样本的各向铺层热阻数据,便得到分别关于R0、R45、R-45、R90数值的4 个样本。再计算得到此样本的平均值,便得到了不同温度下-45°、45°、0°和90°铺层热阻平均值、。然后,根据待预测试样的铺层顺序,再次采用串联热阻理论,计算得到当前铺层复材的热阻预测值
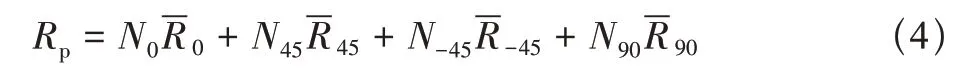
再结合该试样铺层层数N便可得Z向热导率预测值

2 X/Y向热导率预测方法
X/Y向传热并联模型如图3所示,根据传递的总热量一致,可以建立以下方程
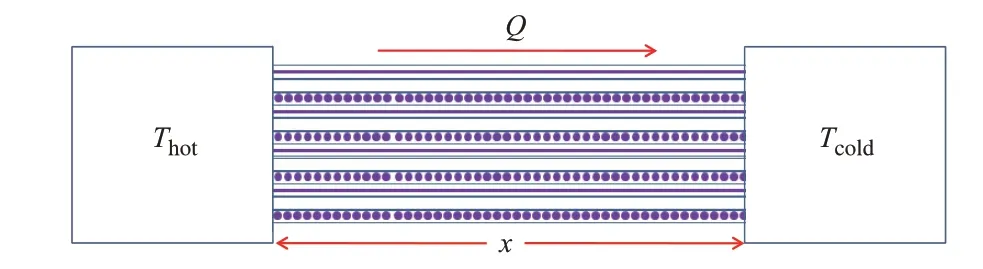
图3 X/Y向传热并联模型Fig.3 Shunt‐wound thermal conduction model in X/Y‐orientation
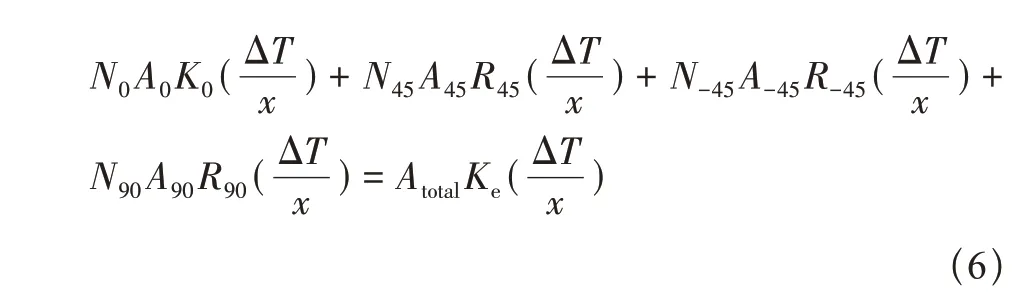
式中:下标代表单一铺层角度;N为相应角度铺层的层数;A为相应角度铺层的横截面积;x为试样厚度;Atotal为试样总截面积;Ke为复材试样的等效热导率;ΔT为热端与冷端的温差。式(6)可进一步简化为
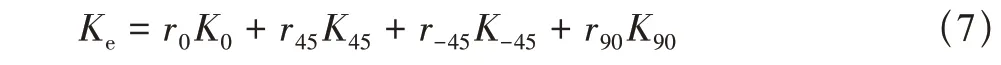
式中:r代表各角度铺层占总层数的比例。
当得到一批试样的实测数据之后,可以利用式(7)参照Z向热导率的预测方法求出同一温度下-45°、45°、0°和90°铺层热导率平均值,然后再利用式(7)求出待预测铺层的X/Y向热导率。但是,从式(7)中可以看到,X向或Y向热导率与不同角度铺层的占比有关,由于LFA 检测区域内包含的只是一部分铺层(见图4),测试获取的并不是试样整体沿X向或Y向的等效热导率,并且受检测区域形状影响,不同角度铺层在其中的位置不同则横截面积不同,式(7)并不适用,单层铺层对测得的热导率数据的贡献跟其处在检测区域中的位置有关。
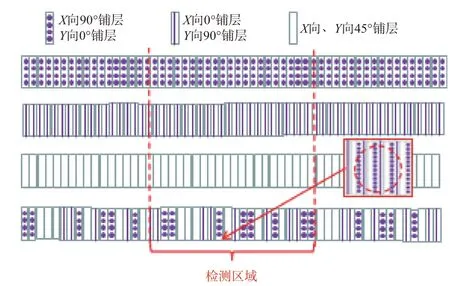
图4 LFA检测区域示意图Fig.4 Sketch map of detection area of LFA
当试样为单一角度θ铺层时,如纯0°铺层、纯45°铺层,由于该角度所有铺层的总面积等于试样总面积,式(7)可以简化为

式中:Kθ为该角度铺层的热导率。从式(8)可以看到,对于单一角度铺层的试样,测得的热导率可以认为是该角度铺层的热导率。通过测试由单一角度铺层组成的层合板X向和Y向热导率,就可以采用式(7)对常规非单一角度铺层的热导率进行计算。由对称性可知,0°铺层的X向和Y向热导率应分别与90°铺层的Y向和X向热导率相同,而45°铺层的X向和Y向热导率与-45°铺层相同,因此在实际测试中只需要测试纯0°铺层和纯45°铺层的试样在X向和Y向的热导率,就可以采用式(7)预测采用常规铺层方式的试样的热导率。
3 热导率测试
试样为88种采用不同铺层方式的复合材料层合板,平面尺寸分为8mm×8mm和10mm×10mm两种,厚度2~6mm,每种试验件有两件,共计176件,用于测试Z向热导率的试验件有28种共56件,用于测试X/Y向热导率的试验件均为30 种共60 件。试验件外形如图5 所示,取样方向如图6 所示,部分铺层信息见表1,X向和Y向试样中包含纯0°和纯45°铺层试样,其余均为一般混杂铺层,并且除单一角度铺层试样外,X向和Y向试样的铺层顺序是Z向试验铺层的若干次循环叠加,以满足测试对试样平面尺寸的要求。每件试验件依次进行-70℃、-50℃、-30℃、-10℃、10℃、30℃、50℃、70℃、90℃共9种温度环境下的热导率测试。测试装置为耐驰LFA467激光导热仪(见图7)。
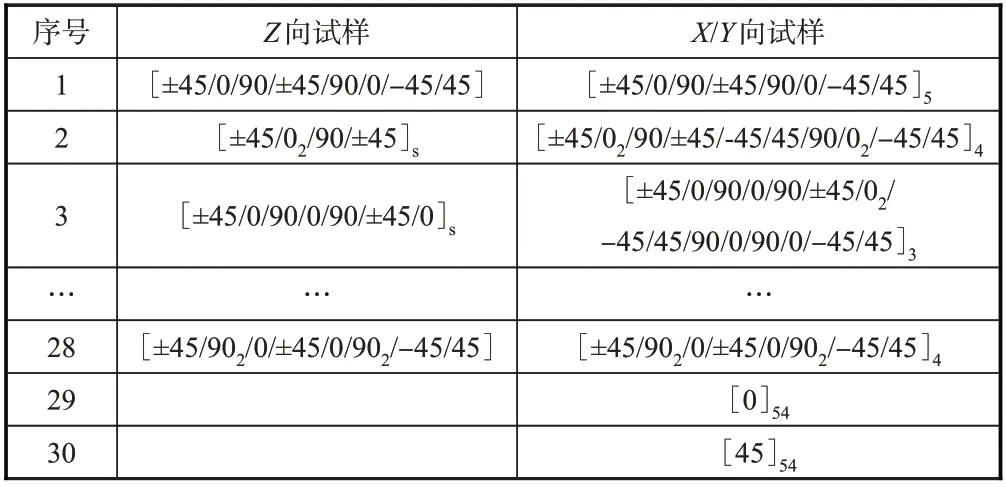
表1 试样铺层顺序Table 1 Stacking sequence of test samples

图5 试样Fig.5 Test samples
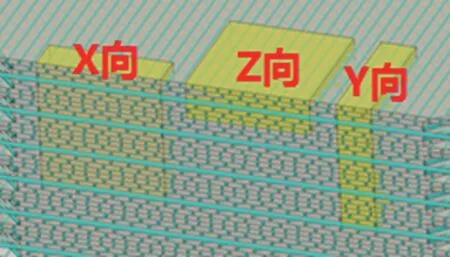
图6 取样方向Fig.6 Sampling orientation

图7 LFA467激光导热仪Fig.7 LFA467 laser flash apparatus
4 预测值与实测值对比
首先利用表1 中Z向试样实测得到的28 种铺层在9 种温度环境下的Z向热导率实测数据(共计252个),以及X/Y向试样实测得到的30种铺层在9种温度环境下的X/Y向热导率实测数据(X、Y向各270个),按照前述热导率预测方法计算得到各试样在相应温度下的热导率预测值。为分析热导率预测方法的预测精度,对比实测值与相应铺层顺序下的预测值之间的相对误差,相对误差按式(9)计算

将预测值与实测值的相对误差分别在1%、3%、5%、10%、15%和20%以内的数据个数进行统计,计算不同相对误差范围内的数据占比,三个方向预测值与实测值相对误差分布情况如图8~图10所示。由此可以看到,在当前测试数据下96%的Z向热导率和97%的X向热导率预测值和实测值相对误差在20%以内,85%的Y向预测值和实测值相对误差在20%以内。相较于参考文献[5]中基于纤维和基体热导率,采用三种预测模型得到的单向铺层热导率预测结果与实测结果之间仅有40%(parallel model)、67%(network model G)、7%(network model H)的数据相对误差在20%以内,本方法预测精度较高。此处X向和Y向热导率预测值是采用纯0°铺层和纯45°铺层的热导率数据按照式(7)进行预测的,在前述内容中提到对于一般混杂铺层,LFA测试到的不是试样整体沿X向或Y向的等效热导率,之所以预测值仍然与LFA 实测值整体比较接近,是由于用于测试X向和Y向热导率的试样铺层方式为一定铺层顺序的循环排列,因此检测区域的传热特性与整体的传热特性比较接近。

图8 Z向预测值与实测值相对误差分布情况Fig.8 Distribution of relative error between the predicted and test value in Z‐orientation
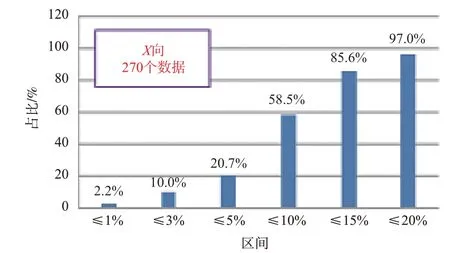
图9 X向预测值与实测值相对误差分布情况Fig.9 Distribution of relative error between the predicted and test value in X‐orientation
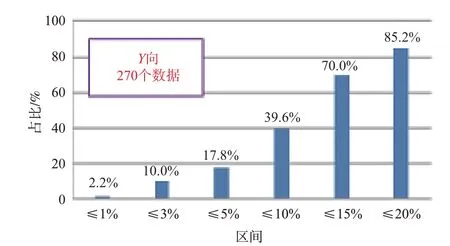
图10 Y向预测值与实测值相对误差分布情况Fig.10 Distribution of relative error between the predicted and test value in Y‐orientation
5 结论
针对一般混杂铺层的复合材料层合板,提出了预测其X向、Y向和Z向等效热导率的预测方法,指出了LFA 在测试层合板X/Y向等效热导率方面的局限性,得到了以下结论:
(1)混杂铺层层合板等效热导率与单向铺层热导率的关系可以用X/Y向热导率并联传热模型、Z向热导率串联传热模型描述。
(2)LFA 在测试单一角度铺层试样X/Y向热导率时可以认为测得的是等效热导率,而测试一般混杂铺层X/Y向热导率时测得结果并不代表等效热导率。
(3)提出的复材层合板三向热导率预测方法不依赖纤维和基体数据、不包含复杂参数、适用于混杂铺层试样,预测精度较高。
